La grille rectangulaire familière est un système facile à apprendre, mais il n'est pas pratique dans toutes les situations. Que faire si vous voulez tracer les rayons sur une roue ou le mouvement de l'eau dans un drain? Dans ces cas, un système de coordonnées circulaires est un ajustement plus naturel. En fait, vous avez déjà utilisé l'idée de base des coordonnées polaires dans la vie quotidienne.[1] Si vous localisez la source d'une sirène, par exemple, vous avez besoin de deux informations: à quelle distance se trouve-t-elle et dans quelle direction provient le son. Le système de coordonnées polaires cartographie les points de la même manière, décrivant la distance à partir d'un point fixe et l'angle d'un rayon fixe.
Première partie de quatre:
Tracer des coordonnées polaires
-
 1 Mettre en place le plan polaire. Vous avez probablement déjà représenté des points avec des coordonnées cartésiennes, en utilisant notation pour marquer les emplacements sur une grille rectangulaire. Les coordonnées polaires utilisent un type de graphique différent, basé sur des cercles:[2]
1 Mettre en place le plan polaire. Vous avez probablement déjà représenté des points avec des coordonnées cartésiennes, en utilisant notation pour marquer les emplacements sur une grille rectangulaire. Les coordonnées polaires utilisent un type de graphique différent, basé sur des cercles:[2] - Le point central du graphique (ou "origine" dans une grille rectangulaire) est le pôle. Vous pouvez étiqueter ceci avec la lettre O.
- En partant du pôle, tracez une ligne horizontale vers la droite. C'est le axe polaire. Étiquetez l'axe avec des unités comme vous le feriez avec l'axe des x positif sur une grille rectangulaire.
- Si vous avez un papier quadrillé spécial, il comprendra de nombreux cercles de tailles différentes, tous centrés sur le pôle. Vous n'avez pas à les dessiner vous-même si vous utilisez du papier vierge.
-
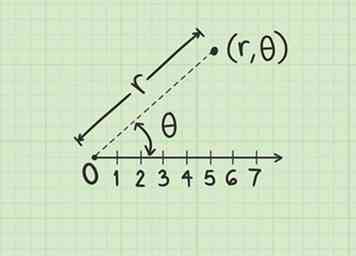 2 Comprendre les coordonnées polaires. Sur le plan polaire, un point est représenté par une coordonnée dans la forme :
2 Comprendre les coordonnées polaires. Sur le plan polaire, un point est représenté par une coordonnée dans la forme : - La première variable, , représente le rayon. Le point est situé sur un cercle de rayon , centré sur le pôle (origine).
- La deuxième variable, , représente un angle. Le point est situé le long d'une ligne qui traverse le poteau et forme un angle avec l'axe polaire.
-
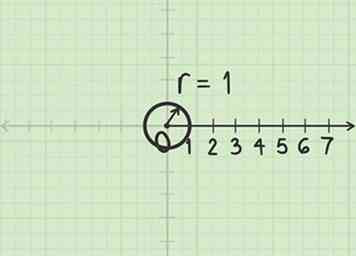 3 Examinez le cercle d'unités. En coordonnées polaires, l'angle est généralement mesuré en radians au lieu de degrés. Dans ce système, une rotation complète (360º ou un cercle complet) couvre un angle de 2 radians. (Cette valeur est choisie car un cercle de rayon 1 a une circonférence de 2.) Familiarisez-vous avec le cercle unitaire pour faciliter le travail avec les coordonnées polaires.
3 Examinez le cercle d'unités. En coordonnées polaires, l'angle est généralement mesuré en radians au lieu de degrés. Dans ce système, une rotation complète (360º ou un cercle complet) couvre un angle de 2 radians. (Cette valeur est choisie car un cercle de rayon 1 a une circonférence de 2.) Familiarisez-vous avec le cercle unitaire pour faciliter le travail avec les coordonnées polaires. - Si votre manuel utilise des degrés, vous n'avez pas besoin de vous en préoccuper pour le moment. Il est possible de tracer des points polaires en utilisant des valeurs de degré pour .
Deuxième partie de quatre:
Tracer un point
-
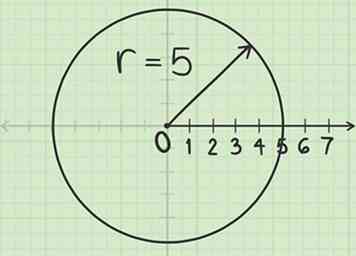 1 Construire un cercle de rayon . N'importe quel moment a des coordonnées polaires sous la forme . Commencez par dessiner un cercle de rayon , centré sur le pôle.
1 Construire un cercle de rayon . N'importe quel moment a des coordonnées polaires sous la forme . Commencez par dessiner un cercle de rayon , centré sur le pôle. - Le pôle est le point central du graphe, l'origine étant sur le plan de coordonnées rectangulaire.
- Par exemple, pour tracer le point , placez votre boussole sur le poteau. Étendre la fin du crayon de la boussole à 5 unités le long de l'axe polaire. Tournez la boussole pour dessiner un cercle.
-
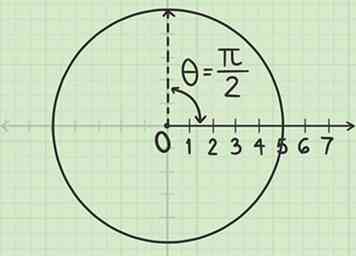 2 Mesurer un angle de de l'axe polaire. Placez un rapporteur de sorte que le centre soit sur le poteau et que le bord longe l'axe polaire. Mesurer l'angle de cet axe. Si l'angle est en radians et que votre rapporteur ne montre que des degrés, vous pouvez convertir les unités ou faire référence au cercle d'unités pour obtenir de l'aide.
2 Mesurer un angle de de l'axe polaire. Placez un rapporteur de sorte que le centre soit sur le poteau et que le bord longe l'axe polaire. Mesurer l'angle de cet axe. Si l'angle est en radians et que votre rapporteur ne montre que des degrés, vous pouvez convertir les unités ou faire référence au cercle d'unités pour obtenir de l'aide. - Pour le point , le cercle de l'unité vous dit que est ¼ du tour autour du cercle, équivalent à 90 degrés de l'axe polaire.
- Toujours mesurer les angles positifs dans le sens inverse des aiguilles d'une montre à partir de l'axe. Mesurer les angles négatifs dans le sens des aiguilles d'une montre à partir de l'axe.
-
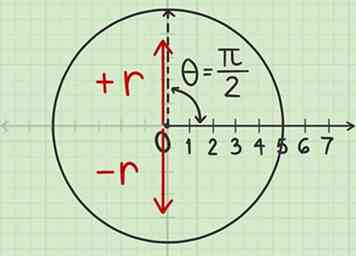 3 Tracez une ligne basée sur le signe de . L'étape suivante consistera à tracer une ligne le long de l'angle que vous avez mesuré. Avant de pouvoir faire cela, vous devez cependant savoir comment tracer la ligne. Reportez-vous aux coordonnées polaires découvrir:
3 Tracez une ligne basée sur le signe de . L'étape suivante consistera à tracer une ligne le long de l'angle que vous avez mesuré. Avant de pouvoir faire cela, vous devez cependant savoir comment tracer la ligne. Reportez-vous aux coordonnées polaires découvrir: - Si est positif, tracez la ligne "vers l’avant", du poteau droit à travers la marque angulaire que vous venez de faire.
- Si est négatif, tracez la ligne "en arrière": de l'angle repérant par le poteau, pour croiser le cercle du côté opposé.
- Ne pas être confondu par des coordonnées rectangulaires: cela ne correspond pas à des valeurs positives ou négatives sur un X- ou y- axe.
-
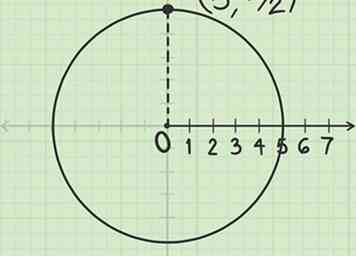 4 Étiquetez le point où la ligne et le cercle se rencontrent. C'est le point .
4 Étiquetez le point où la ligne et le cercle se rencontrent. C'est le point . - Le point est situé sur un cercle de rayon 5 centré sur le pôle, ¼ de la circonférence du cercle dans le sens contraire des aiguilles d'une montre à partir de l'axe polaire. (Ce point est équivalent à (0, 5) en coordonnées rectangulaires.)
Troisième partie de quatre:
Exemples
Premier exemple
Tracer le point P situé à sur le plan polaire
-
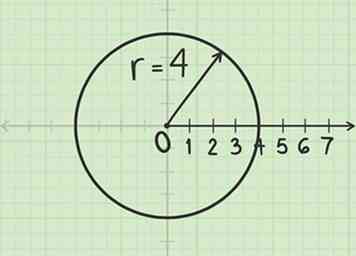 1 Construire un cercle de rayon . Utilisez le pôle comme centre.
1 Construire un cercle de rayon . Utilisez le pôle comme centre. -
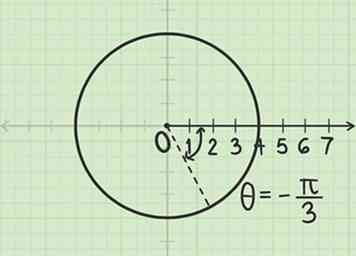 2 Mesurer l'angle radians. Mesurer cet angle par rapport à l'axe polaire (équivalent à l'axe des x positif). Depuis l'angle est négatif, mesure cet angle dans le sens des aiguilles d’une montre.
2 Mesurer l'angle radians. Mesurer cet angle par rapport à l'axe polaire (équivalent à l'axe des x positif). Depuis l'angle est négatif, mesure cet angle dans le sens des aiguilles d’une montre. -
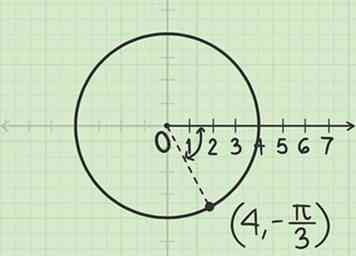 3 Tracez une ligne à cet angle. Commencez au pôle (origine). Puisque le rayon est positif, avancez du pôle à travers l'angle que vous avez mesuré. Le point où la ligne croise le cercle est .
3 Tracez une ligne à cet angle. Commencez au pôle (origine). Puisque le rayon est positif, avancez du pôle à travers l'angle que vous avez mesuré. Le point où la ligne croise le cercle est .
Deuxième exemple
Tracer le point Q situé à sur le plan polaire.
-
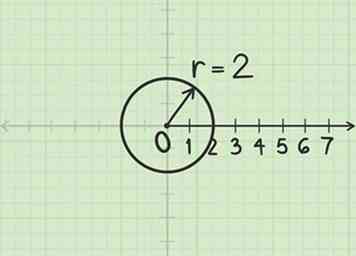 1 Construire un cercle de rayon . Utilisez le pôle comme centre. Bien que le rayon soit en fait -2, le signe n’est pas important pour cette étape.
1 Construire un cercle de rayon . Utilisez le pôle comme centre. Bien que le rayon soit en fait -2, le signe n’est pas important pour cette étape. -
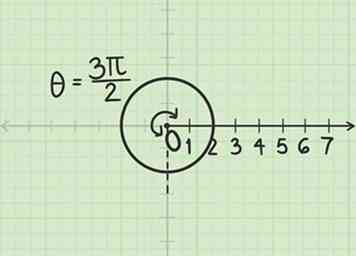 2 Mesurer l'angle radians. Depuis l'angle est positif, vous devez aller dans le sens inverse des aiguilles d’une montre à partir de l’axe polaire.
2 Mesurer l'angle radians. Depuis l'angle est positif, vous devez aller dans le sens inverse des aiguilles d’une montre à partir de l’axe polaire. -
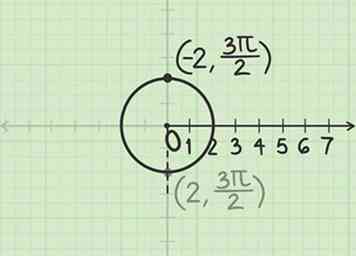 3 Construisez une ligne opposée à cet angle. Depuis le rayon est négatif, vous devez partir du pôle dans le sens inverse de l'angle donné. Le point où la ligne croise le cercle est .
3 Construisez une ligne opposée à cet angle. Depuis le rayon est négatif, vous devez partir du pôle dans le sens inverse de l'angle donné. Le point où la ligne croise le cercle est .
Partie quatre de quatre:
Conversion de coordonnées cartésiennes en coordonnées polaires
-
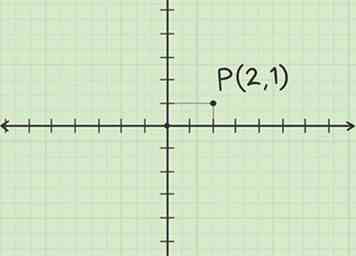 1 Considérez le point dans le plan cartésien. À partir de l'origine, tracez un segment de droite de 2 unités le long du positif X-axe. Tracez un deuxième segment de ligne à partir de ce point 1 unité dans le positif y direction. Vous êtes maintenant au point (2, 1), étiquetez donc ce point P.
1 Considérez le point dans le plan cartésien. À partir de l'origine, tracez un segment de droite de 2 unités le long du positif X-axe. Tracez un deuxième segment de ligne à partir de ce point 1 unité dans le positif y direction. Vous êtes maintenant au point (2, 1), étiquetez donc ce point P. -
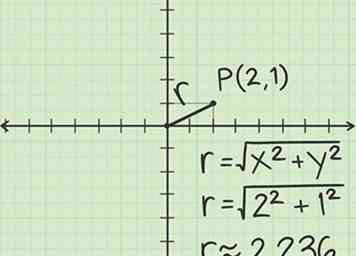 2 Trouver la distance entre l'origine et . Tracez une ligne entre O et P. Cette ligne a la longueur en coordonnées polaires. C'est aussi l'hypoténuse d'un triangle rectangle, vous pouvez donc trouver la longueur de l'hypoténuse en utilisant la géométrie. Par exemple:
2 Trouver la distance entre l'origine et . Tracez une ligne entre O et P. Cette ligne a la longueur en coordonnées polaires. C'est aussi l'hypoténuse d'un triangle rectangle, vous pouvez donc trouver la longueur de l'hypoténuse en utilisant la géométrie. Par exemple: - Les jambes de ce triangle rectangle ont des valeurs de 2 et 1.
- Avec le théorème de Pythagore, calculez que la longueur de l'hypoténuse est .
- La formule générale à trouver à partir des coordonnées cartésiennes est , où est la coordonnée cartésienne x et la coordonnée cartésienne y.
-
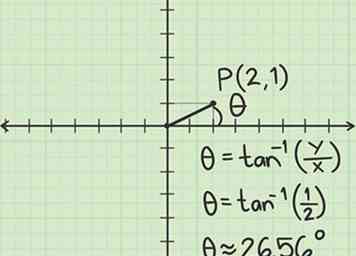 3 Trouvez l'angle entre et l'axe des x positif. Utilisez la trigonométrie pour trouver cette valeur:
3 Trouvez l'angle entre et l'axe des x positif. Utilisez la trigonométrie pour trouver cette valeur: -
- La formule générale à trouver est , où est la coordonnée cartésienne y et la coordonnée cartésienne x.
-
-
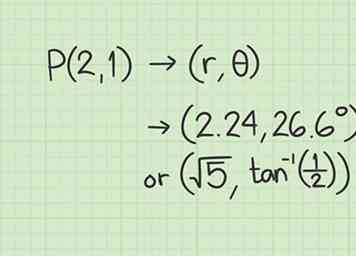 4 Notez les coordonnées polaires. Vous avez maintenant les valeurs de et . Les coordonnées rectangulaires (2, 1) convertissent en coordonnées polaires approximatives de (2,24, 26,6º), ou les coordonnées exactes de .
4 Notez les coordonnées polaires. Vous avez maintenant les valeurs de et . Les coordonnées rectangulaires (2, 1) convertissent en coordonnées polaires approximatives de (2,24, 26,6º), ou les coordonnées exactes de .
 Minotauromaquia
Minotauromaquia
 1 Mettre en place le plan polaire. Vous avez probablement déjà représenté des points avec des coordonnées cartésiennes, en utilisant
1 Mettre en place le plan polaire. Vous avez probablement déjà représenté des points avec des coordonnées cartésiennes, en utilisant  2 Comprendre les coordonnées polaires. Sur le plan polaire, un point est représenté par une coordonnée dans la forme
2 Comprendre les coordonnées polaires. Sur le plan polaire, un point est représenté par une coordonnée dans la forme 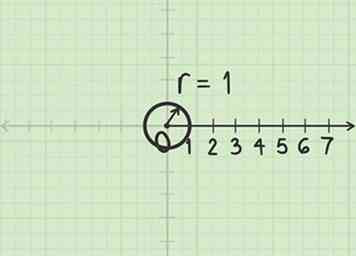 3 Examinez le cercle d'unités. En coordonnées polaires, l'angle est généralement mesuré en radians au lieu de degrés. Dans ce système, une rotation complète (360º ou un cercle complet) couvre un angle de 2
3 Examinez le cercle d'unités. En coordonnées polaires, l'angle est généralement mesuré en radians au lieu de degrés. Dans ce système, une rotation complète (360º ou un cercle complet) couvre un angle de 2 1 Construire un cercle de rayon
1 Construire un cercle de rayon  2 Mesurer un angle de
2 Mesurer un angle de  3 Tracez une ligne basée sur le signe de
3 Tracez une ligne basée sur le signe de  4 Étiquetez le point où la ligne et le cercle se rencontrent. C'est le point
4 Étiquetez le point où la ligne et le cercle se rencontrent. C'est le point  1 Construire un cercle de rayon
1 Construire un cercle de rayon  2 Mesurer l'angle
2 Mesurer l'angle  3 Tracez une ligne à cet angle. Commencez au pôle (origine). Puisque le rayon est positif, avancez du pôle à travers l'angle que vous avez mesuré. Le point où la ligne croise le cercle est
3 Tracez une ligne à cet angle. Commencez au pôle (origine). Puisque le rayon est positif, avancez du pôle à travers l'angle que vous avez mesuré. Le point où la ligne croise le cercle est  1 Construire un cercle de rayon
1 Construire un cercle de rayon  2 Mesurer l'angle
2 Mesurer l'angle  3 Construisez une ligne opposée à cet angle. Depuis le rayon
3 Construisez une ligne opposée à cet angle. Depuis le rayon  1 Considérez le point
1 Considérez le point 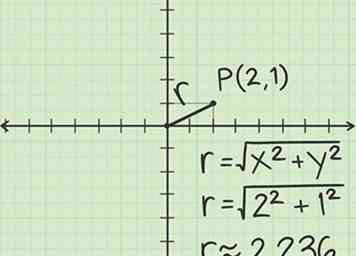 2 Trouver la distance entre l'origine
2 Trouver la distance entre l'origine 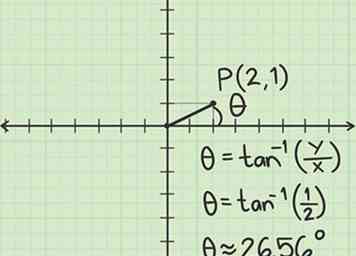 3 Trouvez l'angle entre
3 Trouvez l'angle entre 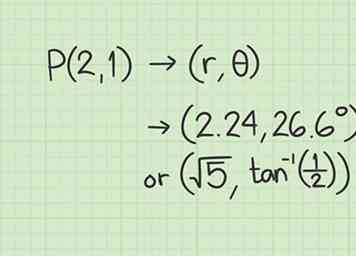 4 Notez les coordonnées polaires. Vous avez maintenant les valeurs de
4 Notez les coordonnées polaires. Vous avez maintenant les valeurs de