L’ensemble de Mandelbrot est constitué de points tracés sur un plan complexe pour former un fractale: une forme ou une forme frappante dans laquelle chaque partie est en fait une copie miniature de l'ensemble. Les images incroyablement éblouissantes cachées dans le set Mandelbrot ont pu être vues dans les années 1500 grâce à la compréhension des nombres imaginaires par Rafael Bombelli - mais ce n'est que Benoît Mandelbrot et d'autres ont commencé à explorer les fractales à l'aide d'ordinateurs. .
Maintenant que nous savons qu'il existe, nous pouvons l'approcher d'une manière plus primitive: à la main. Voici une méthode de visualisation d’un rendu brutal de l’appareil, dans le seul but de comprendre comment cela se fait; vous apprécierez alors beaucoup les rendus que vous pouvez effectuer en utilisant les nombreux programmes informatiques open source disponibles ou que vous pouvez voir sur CD-ROM et DVD.
Pas
-
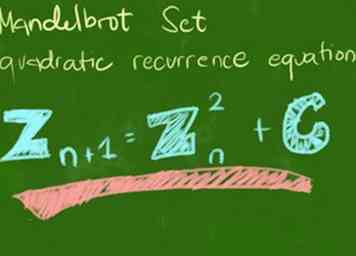 1 Comprendre la formule de base, souvent exprimée comme z = z2 + c. Cela signifie simplement que, pour chaque point de l’univers de Mandelbrot que nous souhaitons voir, nous continuons à calculer z jusqu'à ce que l'une des deux conditions se produisent; Ensuite, nous le colorions pour montrer combien de calculs nous avons faits. Ne vous inquiétez pas! Cela deviendra clair dans les étapes suivantes.
1 Comprendre la formule de base, souvent exprimée comme z = z2 + c. Cela signifie simplement que, pour chaque point de l’univers de Mandelbrot que nous souhaitons voir, nous continuons à calculer z jusqu'à ce que l'une des deux conditions se produisent; Ensuite, nous le colorions pour montrer combien de calculs nous avons faits. Ne vous inquiétez pas! Cela deviendra clair dans les étapes suivantes. -
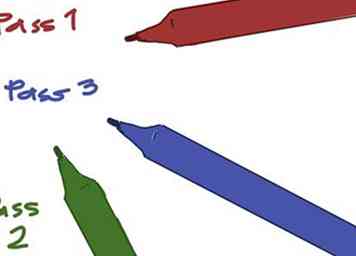
 2 Obtenez 3 crayons de couleur différente, ou des crayons de couleur, ou des marqueurs à pointe de feutre, plus un crayon noir ou un stylo pour faire le contour. La raison pour laquelle nous voulons trois couleurs est que nous allons faire une première approximation avec pas plus de 3 itérations (passes, autrement dit, appliquer la formule jusqu'à 3 fois par point):
2 Obtenez 3 crayons de couleur différente, ou des crayons de couleur, ou des marqueurs à pointe de feutre, plus un crayon noir ou un stylo pour faire le contour. La raison pour laquelle nous voulons trois couleurs est que nous allons faire une première approximation avec pas plus de 3 itérations (passes, autrement dit, appliquer la formule jusqu'à 3 fois par point): -
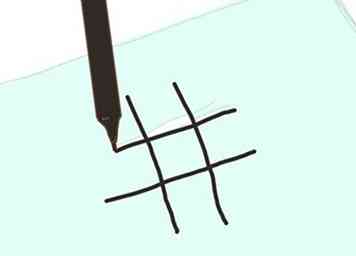 3 Avec le marqueur noir, dessinez une grande planche à tic-tac-toe, 3 par 3 carrés, sur un morceau de papier.
3 Avec le marqueur noir, dessinez une grande planche à tic-tac-toe, 3 par 3 carrés, sur un morceau de papier. -
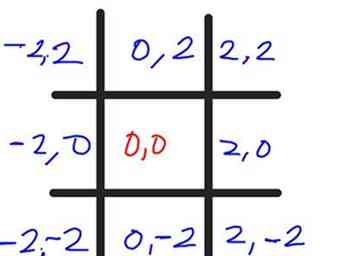 4 Étiquette (également en noir) le carré du milieu (0, 0). Ceci est la constante (c) valeur du point au centre exact du carré. Maintenant, disons que chaque carré est large de 2 unités, alors ajoutez et / ou soustrayez 2 à / de la X et y valeurs de chaque carré, avec X être le premier numéro et y étant le deuxième numéro. Une fois terminé, cela ressemblera à ce que vous voyez ici. Chaque fois que vous suivez les cellules, les valeurs y (le deuxième nombre) doivent être identiques; chaque fois que vous suivez les cellules vers le bas, les valeurs x (le premier nombre) doivent être identiques.
4 Étiquette (également en noir) le carré du milieu (0, 0). Ceci est la constante (c) valeur du point au centre exact du carré. Maintenant, disons que chaque carré est large de 2 unités, alors ajoutez et / ou soustrayez 2 à / de la X et y valeurs de chaque carré, avec X être le premier numéro et y étant le deuxième numéro. Une fois terminé, cela ressemblera à ce que vous voyez ici. Chaque fois que vous suivez les cellules, les valeurs y (le deuxième nombre) doivent être identiques; chaque fois que vous suivez les cellules vers le bas, les valeurs x (le premier nombre) doivent être identiques. - 5 Calculez la première passe ou itération, de la formule. Vous, en tant qu'ordinateur (en réalité, la signification originale du mot était "une personne qui calcule") peut le faire vous-même. Commençons par ces hypothèses:
- La valeur de départ de chaque carré est (0, 0). Lorsque la valeur absolue de z, pour un point donné, est supérieure ou égale à 2, on dit que ce point (et son carré correspondant) ont échappé l'ensemble Mandelbrot. Lorsque cela se produit, vous colorerez le carré en fonction du nombre d'itérations de la formule que vous avez appliquée à ce point.
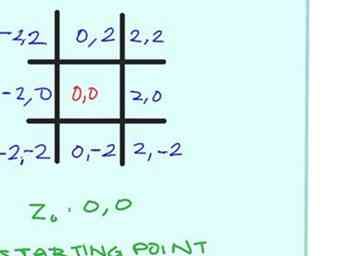
- Choisissez les couleurs que vous utiliserez pour la passe 1, la passe 2 et la passe 3. Supposons respectivement le rouge, le vert et le bleu aux fins de cet article.
- Calculez la valeur de z pour le coin supérieur gauche du tableau tic-tac-toe, en supposant une valeur de départ z de 0 + 0i ou (0, 0) (voir Conseils pour mieux comprendre ces représentations). Nous utilisons la formule z = z2 + c comme indiqué dans la première étape. Vous verrez rapidement que, dans ce cas, z2+ c est simplement c, puisque zéro carré est toujours nul. Et qu'est ce que c'est c pour cette place? (-2, 2).
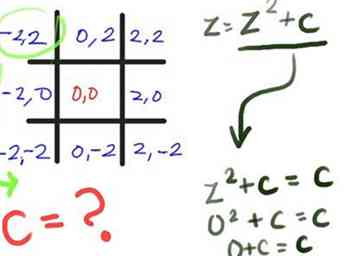
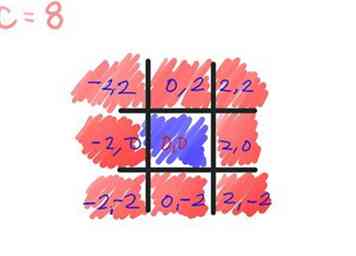
- Détermine la valeur absolue de ce point; la valeur absolue d'un nombre complexe (a, b) est la racine carrée d'un2 + b2. Maintenant, puisque nous allons comparer cela à une valeur connue: 2, nous pouvons éviter de prendre des racines carrées en comparant2 + b2 à 22, que nous connaissons égal 4. Dans ce calcul, a = -2 et b = 2.

- ([-2]2 + 22) =
- (4 + 4) =
- 8, qui est supérieur à 4.
- Il a échappé au jeu de Mandelbrot après le premier calcul, puisque sa valeur absolue est supérieure à 2. Colorie-le avec le crayon que tu as choisi pour passer 1.
-
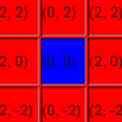 Faites la même chose pour chaque case du plateau, à l'exception du carré central, qui n'échappera pas au set de Mandelbrot par le 3ème passage (ni ne s'échappera jamais). Vous n'avez donc utilisé que deux couleurs: la couleur de passe 1 pour tous les carrés extérieurs et la couleur de passe 3 pour le carré du milieu.
Faites la même chose pour chaque case du plateau, à l'exception du carré central, qui n'échappera pas au set de Mandelbrot par le 3ème passage (ni ne s'échappera jamais). Vous n'avez donc utilisé que deux couleurs: la couleur de passe 1 pour tous les carrés extérieurs et la couleur de passe 3 pour le carré du milieu.
- La valeur de départ de chaque carré est (0, 0). Lorsque la valeur absolue de z, pour un point donné, est supérieure ou égale à 2, on dit que ce point (et son carré correspondant) ont échappé l'ensemble Mandelbrot. Lorsque cela se produit, vous colorerez le carré en fonction du nombre d'itérations de la formule que vous avez appliquée à ce point.
-
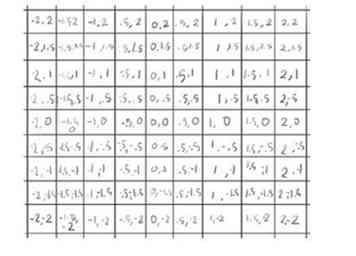 6 Essayons un carré 3 fois plus grand, 9 par 9, tout en conservant un maximum de 3 itérations.
6 Essayons un carré 3 fois plus grand, 9 par 9, tout en conservant un maximum de 3 itérations. - 7 Commencez avec la 3ème rangée, parce que c'est tout de suite intéressant.
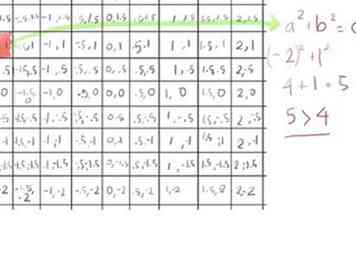
- Le premier élément, (-2, 1) est supérieur à 2 (parce que (-2)2 + 12 se révèle être 5) alors peignons celui-là rouge, car il échappe à l'ensemble de Mandelbrot sur la première passe.
- Le second élément, (-1.5, 1) ne s'avère pas supérieur à 2. Application de la formule pour la valeur absolue, x2+ y2, avec x = -1,5 et y = 1:
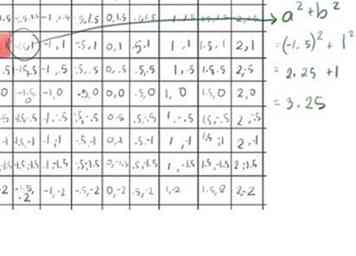
- (-1.5)2 = 2.25
- 12 = 1
- 2,25 + 1 = 3,25, moins de 4, donc la racine carrée est inférieure à 2.
- Nous passons donc à notre deuxième passe, en calculant z2+ c en utilisant le raccourci (x2-y2, 2xy) pour z2 (voir Astuces sur la façon dont ce raccourci est dérivé), toujours avec x = -1,5 et y = 1:
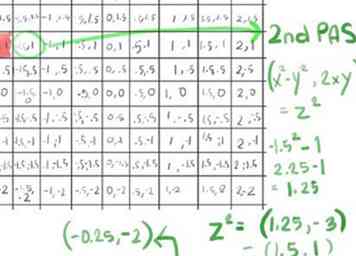
- (-1.5)2 - 12 devient 2,25-1, ce qui devient 1.25;
- 2xy, puisque x est -1.5 et y est 1, devient 2 (-1.5), ce qui donne -3.0;
- Cela nous donne un z2 de (1.25, -3)
- Maintenant ajoutez c pour cette cellule (ajouter x à x, y à y), on obtient (-0,25, -2)
- Testons si sa valeur absolue est maintenant supérieure à 2 :. Calculer x2 + y2:
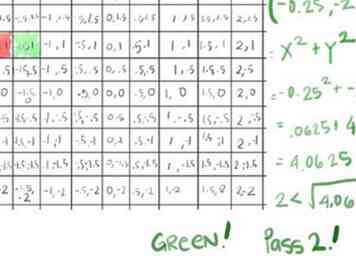
- (-.25)2 = .0625
- -22 = 4
- .0625 + 4 = 4.0625, dont la racine carrée est supérieure à 2, il s'est donc échappé après la deuxième itération: notre premier vert!
- Lorsque vous vous familiariserez avec les calculs, vous serez parfois en mesure de dire lesquels échappent à l'ensemble Mandelbrot en jetant un coup d'œil aux chiffres.Dans cet exemple, le composant y a une magnitude de 2 qui, au carré et ajouté à la valeur au carré de l’autre nombre, sera supérieure à 4. Tout nombre supérieur à 4 aura une racine carrée supérieure à 2. Voir les astuces. ci-dessous pour une explication plus détaillée.
- Le troisième élément, avec une valeur c de (-1, 1), n’échappe pas à la première passe: puisque 1 et -1 au carré sont égaux à 1, x2+ y2 est 2. Nous calculons donc z2+ c, en utilisant le raccourci (x2-y2, 2xy) pour z2:

- (-1)2-12 devient 1-1, ce qui est 0;
- 2xy est alors 2 (-1) = -2;
- z2 = (0, -2)
- addition de c on obtient (0, -2) + (-1, 1) = (-1, -1)
- C'est toujours la même valeur absolue qu'avant (la racine carrée de deux, environ 1,41); continuer avec une troisième itération:
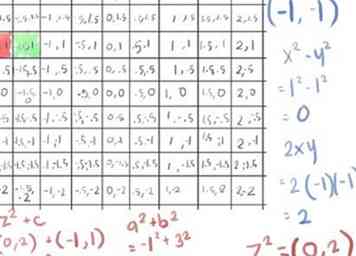
- ([-1]2)-([-1]2) devient 1-1, soit 0 (encore une fois)…
- mais maintenant 2xy est 2 (-1) (- 1), qui est positif 2, donnant un z2 valeur de (0, 2)
- en ajoutant c on obtient (0, 2) + (-1, 1) = (-1, 3), qui a un2 + b2 de 10, beaucoup plus que 4.
- Ainsi, celui-ci s'échappe aussi. Colorez la cellule avec votre troisième couleur, bleue, et passez à la suivante, car nous avons terminé trois itérations avec ce point.
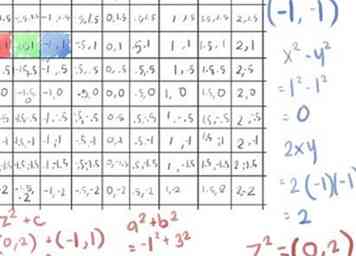
- Le fait que nous n'utilisions que trois couleurs devient un problème ici, car quelque chose qui s'échappe après seulement 3 itérations est coloré comme (0, 0) ce qui jamais s'échappe; De toute évidence, nous ne verrons toujours rien de proche du "bug" de Mandelbrot à ce niveau de détail.
- Le premier élément, (-2, 1) est supérieur à 2 (parce que (-2)2 + 12 se révèle être 5) alors peignons celui-là rouge, car il échappe à l'ensemble de Mandelbrot sur la première passe.
-
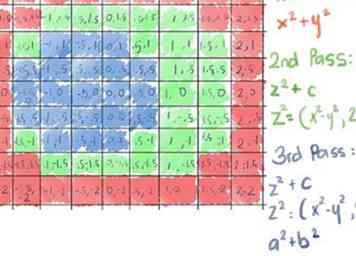 8 Continuer à calculer chaque cellule jusqu'à ce qu'il se soit échappé ou que vous ayez atteint le nombre maximum d'itérations (le nombre de couleurs que vous utilisez: 3 dans cet exemple), à quel point vous le coloriez. Voici comment la matrice 9 by 9 s'occupe de 3 itérations sur chaque carré… On dirait que nous sommes sur quelque chose!
8 Continuer à calculer chaque cellule jusqu'à ce qu'il se soit échappé ou que vous ayez atteint le nombre maximum d'itérations (le nombre de couleurs que vous utilisez: 3 dans cet exemple), à quel point vous le coloriez. Voici comment la matrice 9 by 9 s'occupe de 3 itérations sur chaque carré… On dirait que nous sommes sur quelque chose! - 9 Ré-itérer la même matrice avec plus de couleurs (itérations) pour révéler les couches suivantes, ou mieux, élaborer une matrice beaucoup plus grande pour un projet à plus long terme! Vous obtenez des images plus précises par:
-
 Augmenter le nombre de cellules; cela a 81 cellules par côté. Notez la similarité avec la matrice 9 par 9 ci-dessus, mais les bords beaucoup plus lisses du cercle et de l'ovale.
Augmenter le nombre de cellules; cela a 81 cellules par côté. Notez la similarité avec la matrice 9 par 9 ci-dessus, mais les bords beaucoup plus lisses du cercle et de l'ovale. -
 Augmenter le nombre de couleurs (itérations); Il a 256 nuances de rouge, de vert et de bleu pour un total de 768 couleurs contre 3. Notez que vous pouvez maintenant voir le contour du fameux "lac" de Mandelbrot (ou "bug", selon votre apparence). à elle). L'inconvénient est la quantité de temps qu'il faut; Si vous pouvez calculer chaque itération en 10 secondes, cela représente environ 2 heures pour chaque cellule du lac Mandelbrot ou à proximité. Bien que ce soit une partie relativement petite de la matrice 81 par 81, cela prendrait probablement un an pour la compléter, même si vous y travailliez plusieurs heures par jour. C'est là que le type de silicium de l'ordinateur est pratique.
Augmenter le nombre de couleurs (itérations); Il a 256 nuances de rouge, de vert et de bleu pour un total de 768 couleurs contre 3. Notez que vous pouvez maintenant voir le contour du fameux "lac" de Mandelbrot (ou "bug", selon votre apparence). à elle). L'inconvénient est la quantité de temps qu'il faut; Si vous pouvez calculer chaque itération en 10 secondes, cela représente environ 2 heures pour chaque cellule du lac Mandelbrot ou à proximité. Bien que ce soit une partie relativement petite de la matrice 81 par 81, cela prendrait probablement un an pour la compléter, même si vous y travailliez plusieurs heures par jour. C'est là que le type de silicium de l'ordinateur est pratique.
-
 Minotauromaquia
Minotauromaquia
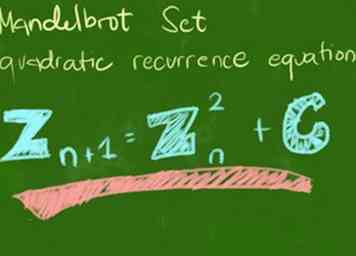 1 Comprendre la formule de base, souvent exprimée comme z = z2 + c. Cela signifie simplement que, pour chaque point de l’univers de Mandelbrot que nous souhaitons voir, nous continuons à calculer z jusqu'à ce que l'une des deux conditions se produisent; Ensuite, nous le colorions pour montrer combien de calculs nous avons faits. Ne vous inquiétez pas! Cela deviendra clair dans les étapes suivantes.
1 Comprendre la formule de base, souvent exprimée comme z = z2 + c. Cela signifie simplement que, pour chaque point de l’univers de Mandelbrot que nous souhaitons voir, nous continuons à calculer z jusqu'à ce que l'une des deux conditions se produisent; Ensuite, nous le colorions pour montrer combien de calculs nous avons faits. Ne vous inquiétez pas! Cela deviendra clair dans les étapes suivantes.  2 Obtenez 3 crayons de couleur différente, ou des crayons de couleur, ou des marqueurs à pointe de feutre, plus un crayon noir ou un stylo pour faire le contour. La raison pour laquelle nous voulons trois couleurs est que nous allons faire une première approximation avec pas plus de 3 itérations (passes, autrement dit, appliquer la formule jusqu'à 3 fois par point):
2 Obtenez 3 crayons de couleur différente, ou des crayons de couleur, ou des marqueurs à pointe de feutre, plus un crayon noir ou un stylo pour faire le contour. La raison pour laquelle nous voulons trois couleurs est que nous allons faire une première approximation avec pas plus de 3 itérations (passes, autrement dit, appliquer la formule jusqu'à 3 fois par point):  3 Avec le marqueur noir, dessinez une grande planche à tic-tac-toe, 3 par 3 carrés, sur un morceau de papier.
3 Avec le marqueur noir, dessinez une grande planche à tic-tac-toe, 3 par 3 carrés, sur un morceau de papier.  4 Étiquette (également en noir) le carré du milieu (0, 0). Ceci est la constante (c) valeur du point au centre exact du carré. Maintenant, disons que chaque carré est large de 2 unités, alors ajoutez et / ou soustrayez 2 à / de la X et y valeurs de chaque carré, avec X être le premier numéro et y étant le deuxième numéro. Une fois terminé, cela ressemblera à ce que vous voyez ici. Chaque fois que vous suivez les cellules, les valeurs y (le deuxième nombre) doivent être identiques; chaque fois que vous suivez les cellules vers le bas, les valeurs x (le premier nombre) doivent être identiques.
4 Étiquette (également en noir) le carré du milieu (0, 0). Ceci est la constante (c) valeur du point au centre exact du carré. Maintenant, disons que chaque carré est large de 2 unités, alors ajoutez et / ou soustrayez 2 à / de la X et y valeurs de chaque carré, avec X être le premier numéro et y étant le deuxième numéro. Une fois terminé, cela ressemblera à ce que vous voyez ici. Chaque fois que vous suivez les cellules, les valeurs y (le deuxième nombre) doivent être identiques; chaque fois que vous suivez les cellules vers le bas, les valeurs x (le premier nombre) doivent être identiques. 

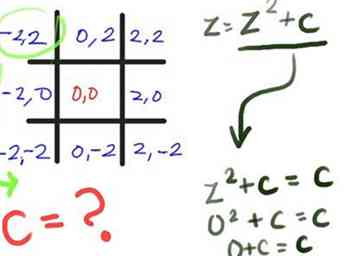


 Faites la même chose pour chaque case du plateau, à l'exception du carré central, qui n'échappera pas au set de Mandelbrot par le 3ème passage (ni ne s'échappera jamais). Vous n'avez donc utilisé que deux couleurs: la couleur de passe 1 pour tous les carrés extérieurs et la couleur de passe 3 pour le carré du milieu.
Faites la même chose pour chaque case du plateau, à l'exception du carré central, qui n'échappera pas au set de Mandelbrot par le 3ème passage (ni ne s'échappera jamais). Vous n'avez donc utilisé que deux couleurs: la couleur de passe 1 pour tous les carrés extérieurs et la couleur de passe 3 pour le carré du milieu. 6 Essayons un carré 3 fois plus grand, 9 par 9, tout en conservant un maximum de 3 itérations.
6 Essayons un carré 3 fois plus grand, 9 par 9, tout en conservant un maximum de 3 itérations. 






 8 Continuer à calculer chaque cellule jusqu'à ce qu'il se soit échappé ou que vous ayez atteint le nombre maximum d'itérations (le nombre de couleurs que vous utilisez: 3 dans cet exemple), à quel point vous le coloriez. Voici comment la matrice 9 by 9 s'occupe de 3 itérations sur chaque carré… On dirait que nous sommes sur quelque chose!
8 Continuer à calculer chaque cellule jusqu'à ce qu'il se soit échappé ou que vous ayez atteint le nombre maximum d'itérations (le nombre de couleurs que vous utilisez: 3 dans cet exemple), à quel point vous le coloriez. Voici comment la matrice 9 by 9 s'occupe de 3 itérations sur chaque carré… On dirait que nous sommes sur quelque chose!  Augmenter le nombre de cellules; cela a 81 cellules par côté. Notez la similarité avec la matrice 9 par 9 ci-dessus, mais les bords beaucoup plus lisses du cercle et de l'ovale.
Augmenter le nombre de cellules; cela a 81 cellules par côté. Notez la similarité avec la matrice 9 par 9 ci-dessus, mais les bords beaucoup plus lisses du cercle et de l'ovale. Augmenter le nombre de couleurs (itérations); Il a 256 nuances de rouge, de vert et de bleu pour un total de 768 couleurs contre 3. Notez que vous pouvez maintenant voir le contour du fameux "lac" de Mandelbrot (ou "bug", selon votre apparence). à elle). L'inconvénient est la quantité de temps qu'il faut; Si vous pouvez calculer chaque itération en 10 secondes, cela représente environ 2 heures pour chaque cellule du lac Mandelbrot ou à proximité. Bien que ce soit une partie relativement petite de la matrice 81 par 81, cela prendrait probablement un an pour la compléter, même si vous y travailliez plusieurs heures par jour. C'est là que le type de silicium de l'ordinateur est pratique.
Augmenter le nombre de couleurs (itérations); Il a 256 nuances de rouge, de vert et de bleu pour un total de 768 couleurs contre 3. Notez que vous pouvez maintenant voir le contour du fameux "lac" de Mandelbrot (ou "bug", selon votre apparence). à elle). L'inconvénient est la quantité de temps qu'il faut; Si vous pouvez calculer chaque itération en 10 secondes, cela représente environ 2 heures pour chaque cellule du lac Mandelbrot ou à proximité. Bien que ce soit une partie relativement petite de la matrice 81 par 81, cela prendrait probablement un an pour la compléter, même si vous y travailliez plusieurs heures par jour. C'est là que le type de silicium de l'ordinateur est pratique.