Un trinôme est une expression algébrique composée de trois termes. Très probablement, vous allez commencer à apprendre à prendre en compte quadratique trinômes, ce qui signifie trinômes écrits dans la forme hache2 + bx + c. Il y a plusieurs astuces à apprendre qui s'appliquent à différents types de trinômes quadratiques, mais vous vous en sortirez de mieux en mieux avec la pratique. Polynômes de degré supérieur, avec des termes comme x3 ou x4, ne peuvent pas toujours être résolus par les mêmes méthodes, mais vous pouvez souvent utiliser une factorisation simple ou une substitution pour les transformer en problèmes pouvant être résolus comme toute formule quadratique.
Méthode One of Three:
Affacturage x2 + bx + c
-
 1 Apprendre la multiplication FOIL. Vous avez peut-être déjà appris la méthode FOIL ou "First, Outside, Inside, Last" pour multiplier les expressions comme (x + 2) (x + 4). Il est utile de savoir comment cela fonctionne avant d'arriver à l'affacturage:
1 Apprendre la multiplication FOIL. Vous avez peut-être déjà appris la méthode FOIL ou "First, Outside, Inside, Last" pour multiplier les expressions comme (x + 2) (x + 4). Il est utile de savoir comment cela fonctionne avant d'arriver à l'affacturage: - Multipliez le Premier termes: (X+2)(X+4) = X2 + __
- Multipliez le À l'extérieur termes: (X+2) (x +4) = x2+4x + __
- Multipliez le À l'intérieur termes: (x +2)(X+4) = x2+ 4x +2x + __
- Multipliez le Dernier termes: (x +2) (x +4) = x2+ 4x + 2x +8
- Simplifier: x2+4x + 2x+8 = x2+6x+8
-
 2 Comprendre l'affacturage. Lorsque vous multipliez deux binômes ensemble dans la méthode FOIL, vous vous retrouvez avec un trinôme (une expression avec trois termes) sous la forme uneX2+bx +c, où a, b et c sont des nombres ordinaires. Si vous commencez avec une équation sous la même forme, vous pouvez la recomposer en deux binômes.
2 Comprendre l'affacturage. Lorsque vous multipliez deux binômes ensemble dans la méthode FOIL, vous vous retrouvez avec un trinôme (une expression avec trois termes) sous la forme uneX2+bx +c, où a, b et c sont des nombres ordinaires. Si vous commencez avec une équation sous la même forme, vous pouvez la recomposer en deux binômes. - Si l'équation n'est pas écrite dans cet ordre, déplacez les termes pour qu'ils le soient. Par exemple, réécrire 3x - 10 + x2 comme X2 + 3x - 10.
- Parce que l'exposant le plus élevé est 2 (x2, ce type d'expression est "quadratique".
-
 3 Écrivez un espace pour la réponse sous la forme FOIL. Pour l'instant, écrivez simplement (__ __)(__ __) dans l'espace où vous allez écrire la réponse. Nous allons le remplir au fur et à mesure.
3 Écrivez un espace pour la réponse sous la forme FOIL. Pour l'instant, écrivez simplement (__ __)(__ __) dans l'espace où vous allez écrire la réponse. Nous allons le remplir au fur et à mesure. - N'écrivez pas encore + ou - entre les termes vides, car nous ne savons pas ce que ce sera.
-
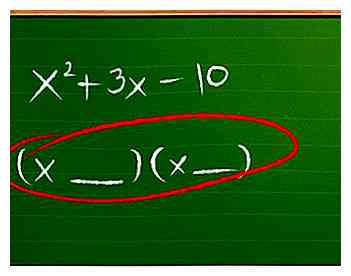 4 Remplissez les premiers termes. Pour des problèmes simples, où le premier terme de votre trinôme est juste x2, les termes en première position seront toujours X et X. Voici les facteurs du terme x2, puisque x fois x = x2.
4 Remplissez les premiers termes. Pour des problèmes simples, où le premier terme de votre trinôme est juste x2, les termes en première position seront toujours X et X. Voici les facteurs du terme x2, puisque x fois x = x2. - Notre exemple x2 + 3x - 10 commence juste par x2, donc on peut écrire:
- (x __) (x __)
- Nous aborderons des problèmes plus complexes dans la section suivante, y compris les trinômes qui commencent par un terme comme 6x2 ou -x2. Pour l'instant, suivez l'exemple du problème.
-
 5 Utilisez l'affacturage pour deviner les derniers termes. Si vous relisez et relisez l'étape de la méthode FOIL, vous verrez que multiplier les derniers termes ensemble vous donne le terme final dans le polynôme (celui sans x). Donc, pour prendre en compte, nous devons trouver deux chiffres qui multiplier pour former le dernier terme.
5 Utilisez l'affacturage pour deviner les derniers termes. Si vous relisez et relisez l'étape de la méthode FOIL, vous verrez que multiplier les derniers termes ensemble vous donne le terme final dans le polynôme (celui sans x). Donc, pour prendre en compte, nous devons trouver deux chiffres qui multiplier pour former le dernier terme. - Dans notre exemple x2 + 3x - 10, le dernier terme est -10.
- Quels sont les facteurs de -10? Quels sont les deux nombres multipliés ensemble égal à -10?
- Il y a plusieurs possibilités: -1 fois 10, 1 fois -10, -2 fois 5 ou 2 fois -5. Écrivez ces paires quelque part pour vous en souvenir.
- Ne changez pas encore notre réponse. Cela ressemble toujours à ceci: (x __) (x __).
-
 6 Testez les possibilités avec la multiplication Outside et Inside. Nous avons réduit les derniers termes à quelques possibilités. Utilisez des essais et des erreurs pour tester chaque possibilité, en multipliant les termes Hors et Intérieur et en comparant le résultat à notre trinôme. Par exemple:
6 Testez les possibilités avec la multiplication Outside et Inside. Nous avons réduit les derniers termes à quelques possibilités. Utilisez des essais et des erreurs pour tester chaque possibilité, en multipliant les termes Hors et Intérieur et en comparant le résultat à notre trinôme. Par exemple: - Notre problème initial a un terme "x" de 3x, donc c'est ce que nous voulons finir dans ce test.
- Test -1 et 10: (x-1) (x + 10). The Outside + Inside = 10x - x = 9x. Nan.
- Test 1 et -10: (x + 1) (x-10). -10x + x = -9x. Ce n'est pas juste. En fait, une fois que vous avez testé -1 et 10, vous savez que 1 et -10 seront juste l'opposé de la réponse ci-dessus: -9x au lieu de 9x.
- Test -2 et 5: (x-2) (x + 5). 5x - 2x = 3x. Cela correspond au polynôme d'origine, donc c'est la bonne réponse: (x-2) (x + 5).
- Dans des cas simples comme celui-ci, quand vous n'avez pas de constante devant le x2 terme, vous pouvez utiliser un raccourci: ajoutez simplement les deux facteurs ensemble et mettez un "x" après (-2 + 5 → 3x). Cela ne fonctionnera pas pour des problèmes plus compliqués, cependant, il est bon de se rappeler le "long chemin" décrit ci-dessus.
Méthode deux sur trois:
Affacturage des Trinomials plus compliqués
-
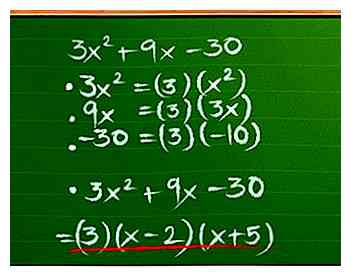 1 Utilisez le factoring simple pour faciliter les problèmes plus compliqués. Disons que vous devez prendre en compte 3x2 + 9x - 30. Cherchez quelque chose qui prend en compte chacun des trois termes (le «plus grand facteur commun» ou GCF).[1] Dans ce cas, c'est 3:
1 Utilisez le factoring simple pour faciliter les problèmes plus compliqués. Disons que vous devez prendre en compte 3x2 + 9x - 30. Cherchez quelque chose qui prend en compte chacun des trois termes (le «plus grand facteur commun» ou GCF).[1] Dans ce cas, c'est 3: - 3x2 = (3) (x2)
- 9x = (3) (3x)
- -30 = (3)(-10)
- Donc 3x2 + 9x - 30 = (3) (x2+ 3x-10). Nous pouvons factoriser le nouveau trinôme en suivant les étapes de la section ci-dessus. Notre réponse finale sera (3) (x-2) (x + 5).
-
 2 Recherchez des facteurs plus délicats. Parfois, le facteur peut impliquer des variables ou il peut être nécessaire de prendre en compte plusieurs fois pour trouver l'expression la plus simple possible. Voici quelques exemples:
2 Recherchez des facteurs plus délicats. Parfois, le facteur peut impliquer des variables ou il peut être nécessaire de prendre en compte plusieurs fois pour trouver l'expression la plus simple possible. Voici quelques exemples: - 2x2y + 14xy + 24y = (2 ans)(X2 + 7x + 12)
- X4 + 11x3 - 26x2 = (X2)(X2 + 11x - 26)
- -X2 + 6x - 9 = (-1)(X2 - 6x + 9)
- N'oubliez pas de prendre en compte le nouveau trinôme en suivant les étapes de la méthode 1. Vérifiez votre travail et trouvez des exemples de problèmes similaires dans les exemples de problèmes au bas de cette page.
-
 3 Résoudre des problèmes avec un nombre devant le x2. Certains trinômes quadratiques ne peuvent pas être simplifiés jusqu'au type de problème le plus facile. Apprenez à résoudre des problèmes comme 3x2 + 10x + 8, alors entraînez-vous seul avec les exemples de problèmes au bas de la page:
3 Résoudre des problèmes avec un nombre devant le x2. Certains trinômes quadratiques ne peuvent pas être simplifiés jusqu'au type de problème le plus facile. Apprenez à résoudre des problèmes comme 3x2 + 10x + 8, alors entraînez-vous seul avec les exemples de problèmes au bas de la page: - Configurez notre réponse: (__ __)(__ __)
- Nos «premiers» termes auront chacun un x, et se multiplieront pour faire 3x2. Il n'y a qu'une seule option possible ici: (3x __) (x __).
- Facteurs de liste de 8. Nos options sont 1 fois 8 ou 2 fois 4.
- Testez-les en utilisant les termes Hors et Intérieur. Notez que l'ordre des facteurs est important, car le terme extérieur est multiplié par 3 au lieu de x. Essayez toutes les possibilités jusqu'à obtenir un résultat Outside + Inside de 10x (à partir du problème d'origine):
- (3x + 1) (x + 8) → 24x + x = 25x non
- (3x + 8) (x + 1) → 3x + 8x = 11x non
- (3x + 2) (x + 4) → 12x + 2x = 14x non
- (3x + 4) (x + 2) → 6x + 4x = 10x Oui C'est le facteur correct.
-
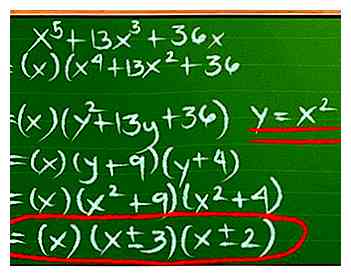 4 Utilisez la substitution pour les trinômes de degré supérieur. Votre livre de mathématiques pourrait vous surprendre avec une équation avec un exposant élevé, tel que x4, même après avoir utilisé la factoring simple pour faciliter le problème. Essayez de remplacer une nouvelle variable pour en faire un problème que vous savez résoudre. Par exemple:
4 Utilisez la substitution pour les trinômes de degré supérieur. Votre livre de mathématiques pourrait vous surprendre avec une équation avec un exposant élevé, tel que x4, même après avoir utilisé la factoring simple pour faciliter le problème. Essayez de remplacer une nouvelle variable pour en faire un problème que vous savez résoudre. Par exemple: - X5+ 13x3+ 36x
- = (x) (x4+ 13x2+36)
- Inventons une nouvelle variable. Nous dirons y = x2et branchez-le:
- (x) (y2+ 13 ans + 36)
- = (x) (y + 9) (y + 4). Revenez maintenant à l'utilisation de la variable d'origine:
- = (x) (x2+9) (x2+4)
- =(x) (x ± 3) (x ± 2)
Méthode trois sur trois:
Affacturage des cas spéciaux
-
 1 Vérifiez les nombres premiers. Vérifiez si la constante dans le premier ou le troisième terme du trinôme est un nombre premier. Un nombre premier ne peut être divisé que par lui-même et par 1, il n'y a donc qu'une seule paire possible de facteurs binomiaux.
1 Vérifiez les nombres premiers. Vérifiez si la constante dans le premier ou le troisième terme du trinôme est un nombre premier. Un nombre premier ne peut être divisé que par lui-même et par 1, il n'y a donc qu'une seule paire possible de facteurs binomiaux. - Par exemple, en x2 + 6x + 5 "5 est un nombre premier, donc le binôme doit être sous la forme (__ 5) (__ 1).
- Dans le problème 3x2+ 10x + 8 3 est un nombre premier, donc le binôme doit être sous la forme (3x __) (x __).
- Pour le problème 3x2+ 4x + 1, les deux 3 et 1 sont des nombres premiers, donc la seule solution possible est (3x + 1) (x + 1). (Vous devriez toujours multiplier cela pour vérifier votre travail, car certaines expressions ne peuvent pas être prises en compte du tout - par exemple, 3x2+ 100x + 1 n'a pas de facteur.)
-
 2 Vérifiez si le trinôme est un carré parfait. Un trinôme carré parfait peut être intégré dans deux binômes identiques, et le facteur est généralement écrit (x + 1)2 au lieu de (x + 1) (x + 1). Voici quelques exemples courants qui ont tendance à apparaître dans les problèmes:
2 Vérifiez si le trinôme est un carré parfait. Un trinôme carré parfait peut être intégré dans deux binômes identiques, et le facteur est généralement écrit (x + 1)2 au lieu de (x + 1) (x + 1). Voici quelques exemples courants qui ont tendance à apparaître dans les problèmes: - X2+ 2x + 1 = (x + 1)2et x2-2x + 1 = (x-1)2
- X2+ 4x + 4 = (x + 2)2et x2-4x + 4 = (x-2)2
- X2+ 6x + 9 = (x + 3)2et x2-6x + 9 = (x-3)2
- Un trinôme carré parfait dans la forme uneX2 + bx + c a toujours une et c des termes qui sont des carrés parfaits (tels que 1, 4, 9, 16 ou 25) et un b terme (positif ou négatif) égal à 2 (√a * √c).[2]
-
 3 Vérifiez si aucune solution n'existe. Tous les trinômes ne peuvent pas être pris en compte. Si vous êtes coincé sur un trinôme quadratique (hache2+ bx + c), utilisez la formule quadratique pour trouver la réponse. Si les seules réponses sont la racine carrée d'un nombre négatif, aucune solution réelle n'existe, il n'y a donc pas de facteurs.
3 Vérifiez si aucune solution n'existe. Tous les trinômes ne peuvent pas être pris en compte. Si vous êtes coincé sur un trinôme quadratique (hache2+ bx + c), utilisez la formule quadratique pour trouver la réponse. Si les seules réponses sont la racine carrée d'un nombre négatif, aucune solution réelle n'existe, il n'y a donc pas de facteurs. - Pour les trinômes non quadratiques, utilisez le critère d'Eisenstein, décrit dans la section Conseils.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Apprendre la multiplication FOIL. Vous avez peut-être déjà appris la méthode FOIL ou "First, Outside, Inside, Last" pour multiplier les expressions comme (x + 2) (x + 4). Il est utile de savoir comment cela fonctionne avant d'arriver à l'affacturage:
1 Apprendre la multiplication FOIL. Vous avez peut-être déjà appris la méthode FOIL ou "First, Outside, Inside, Last" pour multiplier les expressions comme (x + 2) (x + 4). Il est utile de savoir comment cela fonctionne avant d'arriver à l'affacturage:  2 Comprendre l'affacturage. Lorsque vous multipliez deux binômes ensemble dans la méthode FOIL, vous vous retrouvez avec un trinôme (une expression avec trois termes) sous la forme uneX2+bx +c, où a, b et c sont des nombres ordinaires. Si vous commencez avec une équation sous la même forme, vous pouvez la recomposer en deux binômes.
2 Comprendre l'affacturage. Lorsque vous multipliez deux binômes ensemble dans la méthode FOIL, vous vous retrouvez avec un trinôme (une expression avec trois termes) sous la forme uneX2+bx +c, où a, b et c sont des nombres ordinaires. Si vous commencez avec une équation sous la même forme, vous pouvez la recomposer en deux binômes.  3 Écrivez un espace pour la réponse sous la forme FOIL. Pour l'instant, écrivez simplement (__ __)(__ __) dans l'espace où vous allez écrire la réponse. Nous allons le remplir au fur et à mesure.
3 Écrivez un espace pour la réponse sous la forme FOIL. Pour l'instant, écrivez simplement (__ __)(__ __) dans l'espace où vous allez écrire la réponse. Nous allons le remplir au fur et à mesure. 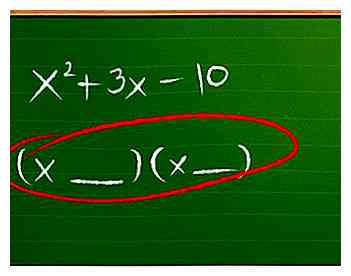 4 Remplissez les premiers termes. Pour des problèmes simples, où le premier terme de votre trinôme est juste x2, les termes en première position seront toujours X et X. Voici les facteurs du terme x2, puisque x fois x = x2.
4 Remplissez les premiers termes. Pour des problèmes simples, où le premier terme de votre trinôme est juste x2, les termes en première position seront toujours X et X. Voici les facteurs du terme x2, puisque x fois x = x2.  5 Utilisez l'affacturage pour deviner les derniers termes. Si vous relisez et relisez l'étape de la méthode FOIL, vous verrez que multiplier les derniers termes ensemble vous donne le terme final dans le polynôme (celui sans x). Donc, pour prendre en compte, nous devons trouver deux chiffres qui multiplier pour former le dernier terme.
5 Utilisez l'affacturage pour deviner les derniers termes. Si vous relisez et relisez l'étape de la méthode FOIL, vous verrez que multiplier les derniers termes ensemble vous donne le terme final dans le polynôme (celui sans x). Donc, pour prendre en compte, nous devons trouver deux chiffres qui multiplier pour former le dernier terme.  6 Testez les possibilités avec la multiplication Outside et Inside. Nous avons réduit les derniers termes à quelques possibilités. Utilisez des essais et des erreurs pour tester chaque possibilité, en multipliant les termes Hors et Intérieur et en comparant le résultat à notre trinôme. Par exemple:
6 Testez les possibilités avec la multiplication Outside et Inside. Nous avons réduit les derniers termes à quelques possibilités. Utilisez des essais et des erreurs pour tester chaque possibilité, en multipliant les termes Hors et Intérieur et en comparant le résultat à notre trinôme. Par exemple: 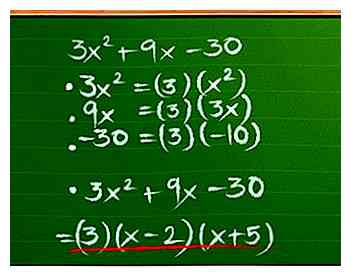 1 Utilisez le factoring simple pour faciliter les problèmes plus compliqués. Disons que vous devez prendre en compte 3x2 + 9x - 30. Cherchez quelque chose qui prend en compte chacun des trois termes (le «plus grand facteur commun» ou GCF).[1] Dans ce cas, c'est 3:
1 Utilisez le factoring simple pour faciliter les problèmes plus compliqués. Disons que vous devez prendre en compte 3x2 + 9x - 30. Cherchez quelque chose qui prend en compte chacun des trois termes (le «plus grand facteur commun» ou GCF).[1] Dans ce cas, c'est 3:  2 Recherchez des facteurs plus délicats. Parfois, le facteur peut impliquer des variables ou il peut être nécessaire de prendre en compte plusieurs fois pour trouver l'expression la plus simple possible. Voici quelques exemples:
2 Recherchez des facteurs plus délicats. Parfois, le facteur peut impliquer des variables ou il peut être nécessaire de prendre en compte plusieurs fois pour trouver l'expression la plus simple possible. Voici quelques exemples:  3 Résoudre des problèmes avec un nombre devant le x2. Certains trinômes quadratiques ne peuvent pas être simplifiés jusqu'au type de problème le plus facile. Apprenez à résoudre des problèmes comme 3x2 + 10x + 8, alors entraînez-vous seul avec les exemples de problèmes au bas de la page:
3 Résoudre des problèmes avec un nombre devant le x2. Certains trinômes quadratiques ne peuvent pas être simplifiés jusqu'au type de problème le plus facile. Apprenez à résoudre des problèmes comme 3x2 + 10x + 8, alors entraînez-vous seul avec les exemples de problèmes au bas de la page: 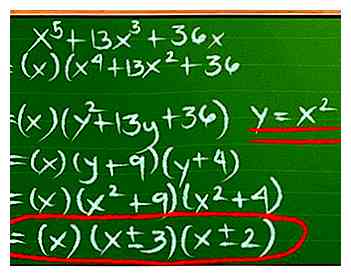 4 Utilisez la substitution pour les trinômes de degré supérieur. Votre livre de mathématiques pourrait vous surprendre avec une équation avec un exposant élevé, tel que x4, même après avoir utilisé la factoring simple pour faciliter le problème. Essayez de remplacer une nouvelle variable pour en faire un problème que vous savez résoudre. Par exemple:
4 Utilisez la substitution pour les trinômes de degré supérieur. Votre livre de mathématiques pourrait vous surprendre avec une équation avec un exposant élevé, tel que x4, même après avoir utilisé la factoring simple pour faciliter le problème. Essayez de remplacer une nouvelle variable pour en faire un problème que vous savez résoudre. Par exemple:  1 Vérifiez les nombres premiers. Vérifiez si la constante dans le premier ou le troisième terme du trinôme est un nombre premier. Un nombre premier ne peut être divisé que par lui-même et par 1, il n'y a donc qu'une seule paire possible de facteurs binomiaux.
1 Vérifiez les nombres premiers. Vérifiez si la constante dans le premier ou le troisième terme du trinôme est un nombre premier. Un nombre premier ne peut être divisé que par lui-même et par 1, il n'y a donc qu'une seule paire possible de facteurs binomiaux.  2 Vérifiez si le trinôme est un carré parfait. Un trinôme carré parfait peut être intégré dans deux binômes identiques, et le facteur est généralement écrit (x + 1)2 au lieu de (x + 1) (x + 1). Voici quelques exemples courants qui ont tendance à apparaître dans les problèmes:
2 Vérifiez si le trinôme est un carré parfait. Un trinôme carré parfait peut être intégré dans deux binômes identiques, et le facteur est généralement écrit (x + 1)2 au lieu de (x + 1) (x + 1). Voici quelques exemples courants qui ont tendance à apparaître dans les problèmes:  3 Vérifiez si aucune solution n'existe. Tous les trinômes ne peuvent pas être pris en compte. Si vous êtes coincé sur un trinôme quadratique (hache2+ bx + c), utilisez la formule quadratique pour trouver la réponse. Si les seules réponses sont la racine carrée d'un nombre négatif, aucune solution réelle n'existe, il n'y a donc pas de facteurs.
3 Vérifiez si aucune solution n'existe. Tous les trinômes ne peuvent pas être pris en compte. Si vous êtes coincé sur un trinôme quadratique (hache2+ bx + c), utilisez la formule quadratique pour trouver la réponse. Si les seules réponses sont la racine carrée d'un nombre négatif, aucune solution réelle n'existe, il n'y a donc pas de facteurs.