Pour diverses raisons, vous devrez peut-être définir la valeur maximale ou minimale d'une fonction quadratique sélectionnée. Vous pouvez trouver le maximum ou le minimum si votre fonction d'origine est écrite sous forme générale, , ou sous forme standard, . Enfin, vous pouvez également utiliser un calcul de base pour définir le maximum ou le minimum de toute fonction quadratique.
Méthode One of Three:
Commençant par la forme générale de la fonction
-
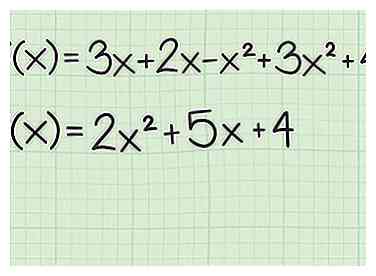 1 Configurez la fonction sous forme générale. Une fonction quadratique est une fonction qui a une terme. Il peut ou non contenir un terme sans exposant. Il n'y aura pas d'exposant supérieur à 2. La forme générale est . Si nécessaire, combinez des termes similaires et réorganisez-les pour définir la fonction sous cette forme générale.[1]
1 Configurez la fonction sous forme générale. Une fonction quadratique est une fonction qui a une terme. Il peut ou non contenir un terme sans exposant. Il n'y aura pas d'exposant supérieur à 2. La forme générale est . Si nécessaire, combinez des termes similaires et réorganisez-les pour définir la fonction sous cette forme générale.[1] - Par exemple, supposons que vous commenciez par . Combinez le termes et la termes pour obtenir les éléments suivants sous forme générale:
- Par exemple, supposons que vous commenciez par . Combinez le termes et la termes pour obtenir les éléments suivants sous forme générale:
-
 2 Détermine la direction du graphique. Une fonction quadratique aboutit au graphique d'une parabole. La parabole s'ouvre soit vers le haut soit vers le bas. Si , le coefficient du terme, est positif, puis la parabole s'ouvre vers le haut. Si est négatif, alors la parabole s'ouvre vers le bas. Regardez les exemples suivants:[2]
2 Détermine la direction du graphique. Une fonction quadratique aboutit au graphique d'une parabole. La parabole s'ouvre soit vers le haut soit vers le bas. Si , le coefficient du terme, est positif, puis la parabole s'ouvre vers le haut. Si est négatif, alors la parabole s'ouvre vers le bas. Regardez les exemples suivants:[2] - Pour , alors la parabole s'ouvre vers le haut.
- Pour , alors la parabole s'ouvre vers le bas.
- Pour , alors la parabole s'ouvre vers le haut.
- Si la parabole s'ouvre vers le haut, vous trouverez sa valeur minimale. Si la parabole s'ouvre vers le bas, vous trouverez sa valeur maximale.
-
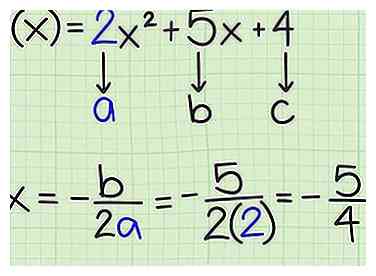 3 Calculer -b / 2a. La valeur de vous dit le valeur du sommet de la parabole. Lorsque la fonction quadratique est écrite sous sa forme générale de , utilisez les coefficients de la et termes comme suit:
3 Calculer -b / 2a. La valeur de vous dit le valeur du sommet de la parabole. Lorsque la fonction quadratique est écrite sous sa forme générale de , utilisez les coefficients de la et termes comme suit: - Pour une fonction , et . Par conséquent, recherchez la valeur x du sommet sous la forme:
- Comme deuxième exemple, considérons la fonction . Dans cet exemple, et . Par conséquent, recherchez la valeur x du sommet sous la forme:
- Pour une fonction , et . Par conséquent, recherchez la valeur x du sommet sous la forme:
-
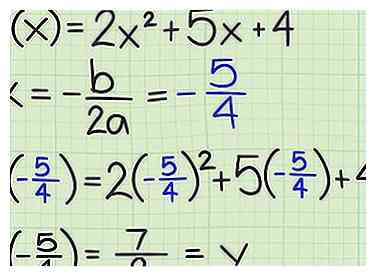 4 Trouvez la valeur f (x) correspondante. Insérez la valeur de x que vous venez de calculer dans la fonction pour trouver la valeur correspondante de f (x). Ce sera le minimum ou le maximum de la fonction.
4 Trouvez la valeur f (x) correspondante. Insérez la valeur de x que vous venez de calculer dans la fonction pour trouver la valeur correspondante de f (x). Ce sera le minimum ou le maximum de la fonction. - Pour le premier exemple ci-dessus, , vous avez calculé la valeur x pour le sommet à être . Entrer au lieu de dans la fonction pour trouver la valeur maximale:
- Pour le deuxième exemple ci-dessus, , vous avez trouvé le sommet à être . Insérer au lieu de dans la fonction pour trouver la valeur maximale:
- Pour le premier exemple ci-dessus, , vous avez calculé la valeur x pour le sommet à être . Entrer au lieu de dans la fonction pour trouver la valeur maximale:
-
 5 Signaler vos résultats. Passez en revue la question qui vous a été posée. Si on vous demande les coordonnées du sommet, vous devez signaler à la fois le et (ou ) valeurs. Si on ne vous demande que le maximum ou le minimum, il vous suffit de déclarer le (ou ) valeur. Reportez-vous à la valeur de la coefficient pour être sûr que vous avez un maximum ou un minimum.
5 Signaler vos résultats. Passez en revue la question qui vous a été posée. Si on vous demande les coordonnées du sommet, vous devez signaler à la fois le et (ou ) valeurs. Si on ne vous demande que le maximum ou le minimum, il vous suffit de déclarer le (ou ) valeur. Reportez-vous à la valeur de la coefficient pour être sûr que vous avez un maximum ou un minimum. - Pour le premier exemple, , la valeur de est positif, vous déclarerez donc la valeur minimale. Le sommet est à , et la valeur minimale est .
- Pour le deuxième exemple, , la valeur de est négatif, vous rapporterez donc la valeur maximale. Le sommet est à , et la valeur maximale est .
Méthode deux sur trois:
Utiliser la forme standard ou vertex
-
 1 Ecrivez votre fonction quadratique en forme standard ou vertex. La forme standard d'une fonction quadratique générale, qui peut aussi s'appeler la forme de sommet, ressemble à ceci:[3]
1 Ecrivez votre fonction quadratique en forme standard ou vertex. La forme standard d'une fonction quadratique générale, qui peut aussi s'appeler la forme de sommet, ressemble à ceci:[3] - Si votre fonction vous est déjà donnée sous cette forme, il vous suffit de reconnaître les variables , et . Si votre fonction commence sous la forme générale , vous devrez compléter le carré pour le réécrire sous forme de sommet.
- Pour voir comment compléter la place, voir Compléter la place.
-
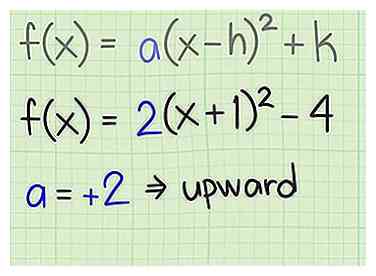 2 Détermine la direction du graphique. Tout comme avec une fonction quadratique écrite dans sa forme générale, vous pouvez indiquer la direction de la parabole en regardant le coefficient . Si dans cette forme standard est positif, alors la parabole s'ouvre vers le haut. Si est négatif, alors la parabole s'ouvre vers le bas. Regardez les exemples suivants:[4]
2 Détermine la direction du graphique. Tout comme avec une fonction quadratique écrite dans sa forme générale, vous pouvez indiquer la direction de la parabole en regardant le coefficient . Si dans cette forme standard est positif, alors la parabole s'ouvre vers le haut. Si est négatif, alors la parabole s'ouvre vers le bas. Regardez les exemples suivants:[4] - Pour , , ce qui est positif, donc la parabole s'ouvre vers le haut.
- Pour , , ce qui est négatif, donc la parabole s'ouvre vers le bas.
- Si la parabole s'ouvre vers le haut, vous trouverez sa valeur minimale. Si la parabole s'ouvre vers le bas, vous trouverez sa valeur maximale.
-
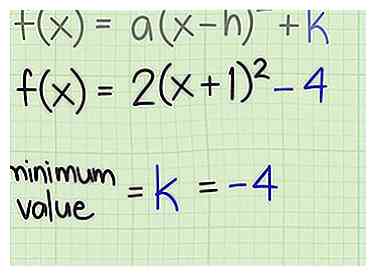 3 Identifier la valeur minimale ou maximale. Lorsque la fonction est écrite sous forme standard, trouver la valeur minimale ou maximale est aussi simple que d'indiquer la valeur de la variable . Pour les deux exemples de fonctions donnés ci-dessus, ces valeurs sont les suivantes:
3 Identifier la valeur minimale ou maximale. Lorsque la fonction est écrite sous forme standard, trouver la valeur minimale ou maximale est aussi simple que d'indiquer la valeur de la variable . Pour les deux exemples de fonctions donnés ci-dessus, ces valeurs sont les suivantes: - Pour , . C'est la valeur minimale de la fonction car cette parabole s'ouvre vers le haut.
- Pour , . C'est la valeur maximale de la fonction, car cette parabole s'ouvre vers le bas.
-
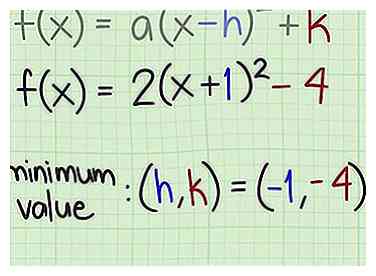 4 Trouvez le sommet. Si on vous demande les coordonnées du minimum ou du maximum, le point sera . Notez, cependant, que dans la forme standard de l’équation, le terme entre parenthèses est , vous avez donc besoin du signe opposé du numéro qui suit le .
4 Trouvez le sommet. Si on vous demande les coordonnées du minimum ou du maximum, le point sera . Notez, cependant, que dans la forme standard de l’équation, le terme entre parenthèses est , vous avez donc besoin du signe opposé du numéro qui suit le . - Pour , le terme entre parenthèses est (x + 1), qui peut être réécrit comme (x - (- 1)). Ainsi, . Par conséquent, les coordonnées du sommet pour cette fonction sont .
- Pour , le terme entre parenthèses est (x-2). Donc, . Les coordonnées du sommet sont (2, 2).
Méthode trois sur trois:
Utilisation du calcul pour calculer le minimum ou le maximum
-
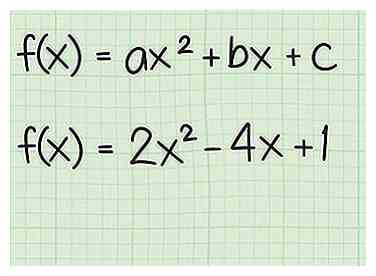 1 Commencez avec la forme générale. Ecrivez votre fonction quadratique sous forme générale, . Si nécessaire, vous devrez peut-être combiner des termes similaires et réorganiser pour obtenir le formulaire approprié.[5]
1 Commencez avec la forme générale. Ecrivez votre fonction quadratique sous forme générale, . Si nécessaire, vous devrez peut-être combiner des termes similaires et réorganiser pour obtenir le formulaire approprié.[5] - Commencez avec la fonction exemple .
-
 2 Utilisez la règle de puissance pour trouver la première dérivée. En utilisant le calcul de base de première année, vous pouvez trouver la première dérivée de la fonction quadratique générale à être .[6]
2 Utilisez la règle de puissance pour trouver la première dérivée. En utilisant le calcul de base de première année, vous pouvez trouver la première dérivée de la fonction quadratique générale à être .[6] - Pour la fonction échantillon , trouvez le dérivé comme:
- Pour la fonction échantillon , trouvez le dérivé comme:
-
 3 Définissez la dérivée égale à zéro. Rappelez-vous que la dérivée d’une fonction vous indique la pente de la fonction à ce point sélectionné. Le minimum ou le maximum d'une fonction se produit lorsque la pente est nulle. Par conséquent, pour trouver où le minimum ou le maximum se produit, définissez la dérivée égale à zéro. Continuez avec le problème ci-dessus:[7]
3 Définissez la dérivée égale à zéro. Rappelez-vous que la dérivée d’une fonction vous indique la pente de la fonction à ce point sélectionné. Le minimum ou le maximum d'une fonction se produit lorsque la pente est nulle. Par conséquent, pour trouver où le minimum ou le maximum se produit, définissez la dérivée égale à zéro. Continuez avec le problème ci-dessus:[7] -
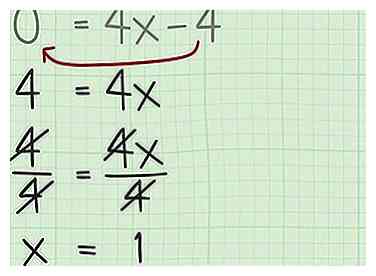 4 Résoudre pour x. Utilisez les règles de base de l'algèbre pour réorganiser la fonction et résoudre la valeur de x lorsque la dérivée est égale à zéro. Cette solution vous indiquera la coordonnée x du sommet de la fonction, qui correspond au maximum ou au minimum.[8]
4 Résoudre pour x. Utilisez les règles de base de l'algèbre pour réorganiser la fonction et résoudre la valeur de x lorsque la dérivée est égale à zéro. Cette solution vous indiquera la coordonnée x du sommet de la fonction, qui correspond au maximum ou au minimum.[8] -
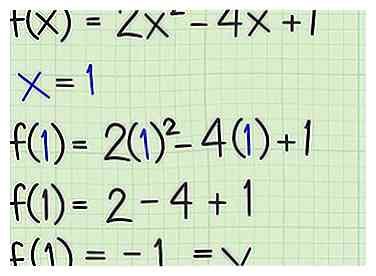 5 Insérez la valeur résolue de x dans la fonction d'origine. La valeur minimum ou maximum de la fonction sera la valeur pour à la sélection position. Insérez votre valeur de dans la fonction d'origine et résoudre pour trouver le minimum ou le maximum.[9]
5 Insérez la valeur résolue de x dans la fonction d'origine. La valeur minimum ou maximum de la fonction sera la valeur pour à la sélection position. Insérez votre valeur de dans la fonction d'origine et résoudre pour trouver le minimum ou le maximum.[9] - Pour la fonction à ,
- Pour la fonction à ,
-
 6 Signaler votre solution La solution vous donne le sommet du point maximum ou minimum. Pour cet exemple de fonction, , le sommet se produit à . Le coefficient est positif, la fonction s'ouvre donc vers le haut. Par conséquent, la valeur minimale de la fonction est la coordonnée y du sommet, qui est .[10]
6 Signaler votre solution La solution vous donne le sommet du point maximum ou minimum. Pour cet exemple de fonction, , le sommet se produit à . Le coefficient est positif, la fonction s'ouvre donc vers le haut. Par conséquent, la valeur minimale de la fonction est la coordonnée y du sommet, qui est .[10]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
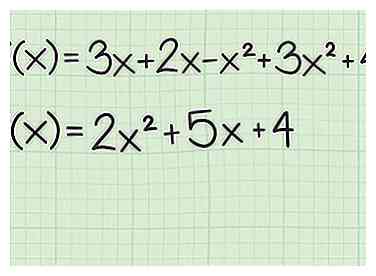 1 Configurez la fonction sous forme générale. Une fonction quadratique est une fonction qui a une
1 Configurez la fonction sous forme générale. Une fonction quadratique est une fonction qui a une  2 Détermine la direction du graphique. Une fonction quadratique aboutit au graphique d'une parabole. La parabole s'ouvre soit vers le haut soit vers le bas. Si
2 Détermine la direction du graphique. Une fonction quadratique aboutit au graphique d'une parabole. La parabole s'ouvre soit vers le haut soit vers le bas. Si 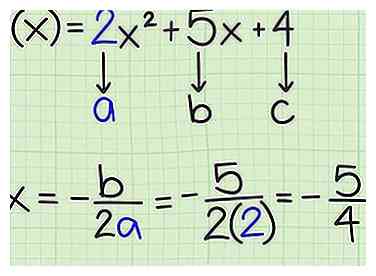 3 Calculer -b / 2a. La valeur de
3 Calculer -b / 2a. La valeur de 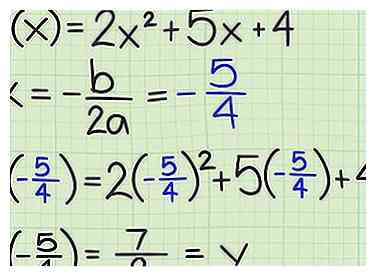 4 Trouvez la valeur f (x) correspondante. Insérez la valeur de x que vous venez de calculer dans la fonction pour trouver la valeur correspondante de f (x). Ce sera le minimum ou le maximum de la fonction.
4 Trouvez la valeur f (x) correspondante. Insérez la valeur de x que vous venez de calculer dans la fonction pour trouver la valeur correspondante de f (x). Ce sera le minimum ou le maximum de la fonction.  5 Signaler vos résultats. Passez en revue la question qui vous a été posée. Si on vous demande les coordonnées du sommet, vous devez signaler à la fois le
5 Signaler vos résultats. Passez en revue la question qui vous a été posée. Si on vous demande les coordonnées du sommet, vous devez signaler à la fois le  1 Ecrivez votre fonction quadratique en forme standard ou vertex. La forme standard d'une fonction quadratique générale, qui peut aussi s'appeler la forme de sommet, ressemble à ceci:[3]
1 Ecrivez votre fonction quadratique en forme standard ou vertex. La forme standard d'une fonction quadratique générale, qui peut aussi s'appeler la forme de sommet, ressemble à ceci:[3] 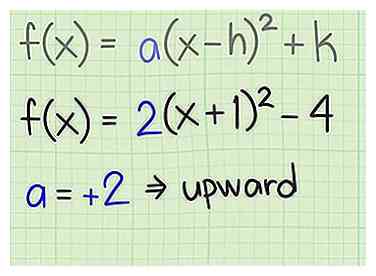 2 Détermine la direction du graphique. Tout comme avec une fonction quadratique écrite dans sa forme générale, vous pouvez indiquer la direction de la parabole en regardant le coefficient
2 Détermine la direction du graphique. Tout comme avec une fonction quadratique écrite dans sa forme générale, vous pouvez indiquer la direction de la parabole en regardant le coefficient 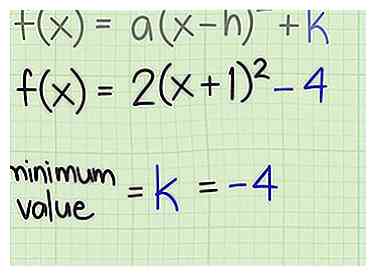 3 Identifier la valeur minimale ou maximale. Lorsque la fonction est écrite sous forme standard, trouver la valeur minimale ou maximale est aussi simple que d'indiquer la valeur de la variable
3 Identifier la valeur minimale ou maximale. Lorsque la fonction est écrite sous forme standard, trouver la valeur minimale ou maximale est aussi simple que d'indiquer la valeur de la variable 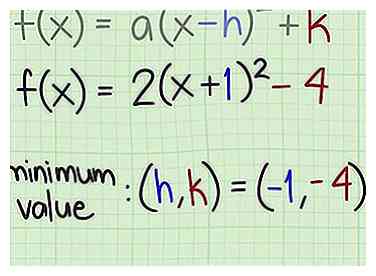 4 Trouvez le sommet. Si on vous demande les coordonnées du minimum ou du maximum, le point sera
4 Trouvez le sommet. Si on vous demande les coordonnées du minimum ou du maximum, le point sera 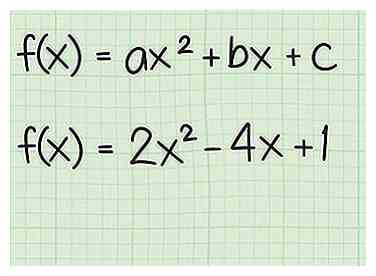 1 Commencez avec la forme générale. Ecrivez votre fonction quadratique sous forme générale,
1 Commencez avec la forme générale. Ecrivez votre fonction quadratique sous forme générale,  2 Utilisez la règle de puissance pour trouver la première dérivée. En utilisant le calcul de base de première année, vous pouvez trouver la première dérivée de la fonction quadratique générale à être
2 Utilisez la règle de puissance pour trouver la première dérivée. En utilisant le calcul de base de première année, vous pouvez trouver la première dérivée de la fonction quadratique générale à être  3 Définissez la dérivée égale à zéro. Rappelez-vous que la dérivée d’une fonction vous indique la pente de la fonction à ce point sélectionné. Le minimum ou le maximum d'une fonction se produit lorsque la pente est nulle. Par conséquent, pour trouver où le minimum ou le maximum se produit, définissez la dérivée égale à zéro. Continuez avec le problème ci-dessus:[7]
3 Définissez la dérivée égale à zéro. Rappelez-vous que la dérivée d’une fonction vous indique la pente de la fonction à ce point sélectionné. Le minimum ou le maximum d'une fonction se produit lorsque la pente est nulle. Par conséquent, pour trouver où le minimum ou le maximum se produit, définissez la dérivée égale à zéro. Continuez avec le problème ci-dessus:[7] 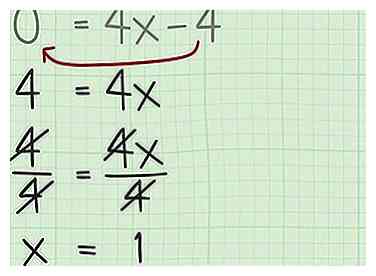 4 Résoudre pour x. Utilisez les règles de base de l'algèbre pour réorganiser la fonction et résoudre la valeur de x lorsque la dérivée est égale à zéro. Cette solution vous indiquera la coordonnée x du sommet de la fonction, qui correspond au maximum ou au minimum.[8]
4 Résoudre pour x. Utilisez les règles de base de l'algèbre pour réorganiser la fonction et résoudre la valeur de x lorsque la dérivée est égale à zéro. Cette solution vous indiquera la coordonnée x du sommet de la fonction, qui correspond au maximum ou au minimum.[8] 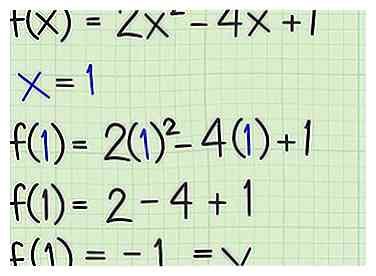 5 Insérez la valeur résolue de x dans la fonction d'origine. La valeur minimum ou maximum de la fonction sera la valeur pour
5 Insérez la valeur résolue de x dans la fonction d'origine. La valeur minimum ou maximum de la fonction sera la valeur pour  6 Signaler votre solution La solution vous donne le sommet du point maximum ou minimum. Pour cet exemple de fonction,
6 Signaler votre solution La solution vous donne le sommet du point maximum ou minimum. Pour cet exemple de fonction,