En algèbre, les graphes de coordonnées à deux dimensions ont un axe horizontal ou un axe des abscisses et un axe vertical ou un axe des ordonnées. Les endroits où des lignes représentant une plage de valeurs traversent ces axes sont appelées interceptions. L'ordonnée à l'origine est l'endroit où la ligne croise l'axe des y et l'interception des x où la ligne traverse l'axe des x. Pour des problèmes simples, il est facile de trouver l'interception X en regardant un graphique. Vous pouvez trouver le point exact de l'interception en résolvant algébriquement en utilisant l'équation de la ligne.
Méthode One of Three:
Utiliser un graphique d'une ligne
-
 1 Identifiez l'axe des x. Un graphique de coordonnées a un axe des ordonnées et un axe des x. L'axe des x est la ligne horizontale (la ligne qui va de gauche à droite). L'axe des y est la ligne verticale (la ligne qui monte et descend).[1] Il est important de regarder l’axe des abscisses lors de la localisation de l’interception x.
1 Identifiez l'axe des x. Un graphique de coordonnées a un axe des ordonnées et un axe des x. L'axe des x est la ligne horizontale (la ligne qui va de gauche à droite). L'axe des y est la ligne verticale (la ligne qui monte et descend).[1] Il est important de regarder l’axe des abscisses lors de la localisation de l’interception x. -
 2 Trouvez le point où la ligne croise l'axe des x. L'interception x est ce point.[2] Si on vous demande de trouver l'interception x basée sur le graphique, le point sera probablement exact (par exemple, au point 4). Cependant, vous devrez généralement utiliser cette méthode (par exemple, le point se situe entre 4 et 5).
2 Trouvez le point où la ligne croise l'axe des x. L'interception x est ce point.[2] Si on vous demande de trouver l'interception x basée sur le graphique, le point sera probablement exact (par exemple, au point 4). Cependant, vous devrez généralement utiliser cette méthode (par exemple, le point se situe entre 4 et 5). -
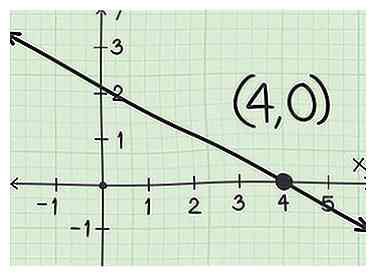 3 Écrivez la paire ordonnée pour l'ordonnée à l'origine. Une paire ordonnée est écrite sous la forme et vous donne les coordonnées du point.[3] Le premier nombre de la paire est le point où la ligne croise l'axe des x (l'ordonnée à l'origine). Le deuxième chiffre pour sera toujours 0, car un point sur l'axe des x n'aura jamais de valeur pour y.[4]
3 Écrivez la paire ordonnée pour l'ordonnée à l'origine. Une paire ordonnée est écrite sous la forme et vous donne les coordonnées du point.[3] Le premier nombre de la paire est le point où la ligne croise l'axe des x (l'ordonnée à l'origine). Le deuxième chiffre pour sera toujours 0, car un point sur l'axe des x n'aura jamais de valeur pour y.[4] - Par exemple, si une ligne coupe l’axe des x au point 4, la paire ordonnée pour l’interception x est .
Méthode deux sur trois:
Utiliser l'équation de la ligne
-
 1 Déterminez que l'équation de la ligne est sous forme standard. La forme standard d'une équation linéaire est .[5] Sous cette forme, , , et sont des entiers, et et sont les coordonnées d'un point sur la ligne.
1 Déterminez que l'équation de la ligne est sous forme standard. La forme standard d'une équation linéaire est .[5] Sous cette forme, , , et sont des entiers, et et sont les coordonnées d'un point sur la ligne. - Par exemple, vous pourriez recevoir l'équation .
-
 2 Branchez 0 pour . L'interception x est le point sur la ligne où la ligne croise l'axe des x.[6] À ce stade, la valeur de sera 0.[7] Donc, pour trouver l'interception x, vous devez définir le à 0 et à résoudre pour .
2 Branchez 0 pour . L'interception x est le point sur la ligne où la ligne croise l'axe des x.[6] À ce stade, la valeur de sera 0.[7] Donc, pour trouver l'interception x, vous devez définir le à 0 et à résoudre pour . - Par exemple, si vous remplacez 0 par , votre équation ressemblera à ceci: , ce qui simplifie à .
-
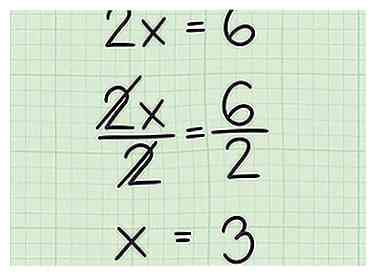 3 Résoudre pour . Pour ce faire, vous devez isoler la variable x en divisant les deux côtés de l’équation par le coefficient. Cela vous donnera la valeur de quand , qui est l'interception x.
3 Résoudre pour . Pour ce faire, vous devez isoler la variable x en divisant les deux côtés de l’équation par le coefficient. Cela vous donnera la valeur de quand , qui est l'interception x. - Par exemple:
- Par exemple:
-
 4 Écrivez la paire ordonnée. Rappelez-vous qu'une paire ordonnée est écrite sous la forme . Pour l’interception x, la valeur de sera la valeur que vous avez calculée précédemment, et la valeur sera 0, depuis est toujours égal à 0 à l'ordonnée à l'origine.[8]
4 Écrivez la paire ordonnée. Rappelez-vous qu'une paire ordonnée est écrite sous la forme . Pour l’interception x, la valeur de sera la valeur que vous avez calculée précédemment, et la valeur sera 0, depuis est toujours égal à 0 à l'ordonnée à l'origine.[8] - Par exemple, pour la ligne , l'ordonnée à l'origine est au point .
Méthode trois sur trois:
Utiliser la formule quadratique
-
 1 Déterminer que l'équation de la ligne est une équation quadratique. Une équation quadratique est une équation qui prend la forme .[9] Une équation quadratique a deux solutions, ce qui signifie qu'une ligne écrite sous cette forme est une parabole et aura deux interceptions x.[10]
1 Déterminer que l'équation de la ligne est une équation quadratique. Une équation quadratique est une équation qui prend la forme .[9] Une équation quadratique a deux solutions, ce qui signifie qu'une ligne écrite sous cette forme est une parabole et aura deux interceptions x.[10] - Par exemple, l'équation est une équation quadratique, donc cette ligne aura deux interceptions x.
-
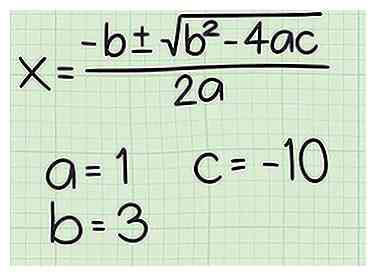 2 Configurez la formule quadratique. La formule est , où est égal au coefficient du terme du second degré (), est égal au coefficient du terme du premier degré (), et est égal à la constante.[11]
2 Configurez la formule quadratique. La formule est , où est égal au coefficient du terme du second degré (), est égal au coefficient du terme du premier degré (), et est égal à la constante.[11] -
 3 Branchez toutes les valeurs dans la formule quadratique. Assurez-vous de substituer les valeurs correctes pour chaque variable de l'équation de la ligne.
3 Branchez toutes les valeurs dans la formule quadratique. Assurez-vous de substituer les valeurs correctes pour chaque variable de l'équation de la ligne. - Par exemple, si l’équation de votre ligne est , votre formule quadratique ressemblera à ceci: .
-
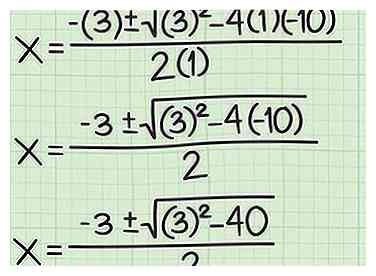 4 Simplifier l'équation. Pour ce faire, complétez d'abord toute la multiplication. Assurez-vous de porter une attention particulière à tous les signes positifs et négatifs.
4 Simplifier l'équation. Pour ce faire, complétez d'abord toute la multiplication. Assurez-vous de porter une attention particulière à tous les signes positifs et négatifs. - Par exemple:
- Par exemple:
-
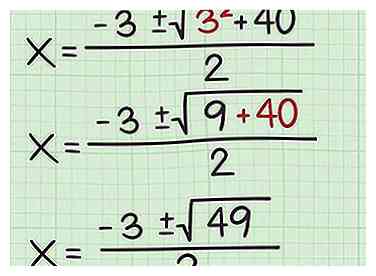 5 Calculez l'exposant. Carré le terme. Ensuite, ajoutez ce numéro à l'autre numéro sous le signe de la racine carrée.
5 Calculez l'exposant. Carré le terme. Ensuite, ajoutez ce numéro à l'autre numéro sous le signe de la racine carrée. - Par exemple:
- Par exemple:
-
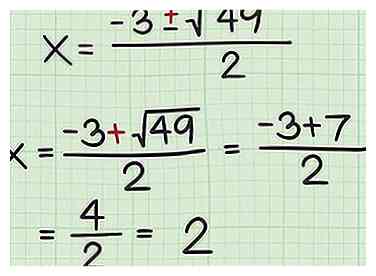 6 Résoudre pour la formule d'addition. Puisque la formule quadratique a un , vous résoudrez une fois en ajoutant, et une fois en soustrayant. Résoudre en ajoutant vous donnera votre première valeur.
6 Résoudre pour la formule d'addition. Puisque la formule quadratique a un , vous résoudrez une fois en ajoutant, et une fois en soustrayant. Résoudre en ajoutant vous donnera votre première valeur. - Par exemple:
- Par exemple:
-
 7 Résoudre pour la formule de soustraction. Cela vous donnera la deuxième valeur pour . Calculez d'abord la racine carrée, puis trouvez la différence dans le numérateur. Enfin, divisez par 2.
7 Résoudre pour la formule de soustraction. Cela vous donnera la deuxième valeur pour . Calculez d'abord la racine carrée, puis trouvez la différence dans le numérateur. Enfin, divisez par 2. - Par exemple:
- Par exemple:
-
 8 Trouvez les paires ordonnées pour l'ordonnée à l'origine. Rappelez-vous qu'une paire ordonnée donne la coordonnée x en premier, puis la coordonnée y . le les valeurs seront les valeurs que vous avez calculées en utilisant la formule quadratique. le la valeur sera 0, car à l'ordonnée à l'origine, toujours égal à 0.[12]
8 Trouvez les paires ordonnées pour l'ordonnée à l'origine. Rappelez-vous qu'une paire ordonnée donne la coordonnée x en premier, puis la coordonnée y . le les valeurs seront les valeurs que vous avez calculées en utilisant la formule quadratique. le la valeur sera 0, car à l'ordonnée à l'origine, toujours égal à 0.[12] - Par exemple, pour la ligne , les interceptions x sont aux points et .
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Identifiez l'axe des x. Un graphique de coordonnées a un axe des ordonnées et un axe des x. L'axe des x est la ligne horizontale (la ligne qui va de gauche à droite). L'axe des y est la ligne verticale (la ligne qui monte et descend).[1] Il est important de regarder l’axe des abscisses lors de la localisation de l’interception x.
1 Identifiez l'axe des x. Un graphique de coordonnées a un axe des ordonnées et un axe des x. L'axe des x est la ligne horizontale (la ligne qui va de gauche à droite). L'axe des y est la ligne verticale (la ligne qui monte et descend).[1] Il est important de regarder l’axe des abscisses lors de la localisation de l’interception x.  2 Trouvez le point où la ligne croise l'axe des x. L'interception x est ce point.[2] Si on vous demande de trouver l'interception x basée sur le graphique, le point sera probablement exact (par exemple, au point 4). Cependant, vous devrez généralement utiliser cette méthode (par exemple, le point se situe entre 4 et 5).
2 Trouvez le point où la ligne croise l'axe des x. L'interception x est ce point.[2] Si on vous demande de trouver l'interception x basée sur le graphique, le point sera probablement exact (par exemple, au point 4). Cependant, vous devrez généralement utiliser cette méthode (par exemple, le point se situe entre 4 et 5).  3 Écrivez la paire ordonnée pour l'ordonnée à l'origine. Une paire ordonnée est écrite sous la forme
3 Écrivez la paire ordonnée pour l'ordonnée à l'origine. Une paire ordonnée est écrite sous la forme  1 Déterminez que l'équation de la ligne est sous forme standard. La forme standard d'une équation linéaire est
1 Déterminez que l'équation de la ligne est sous forme standard. La forme standard d'une équation linéaire est  2 Branchez 0 pour
2 Branchez 0 pour 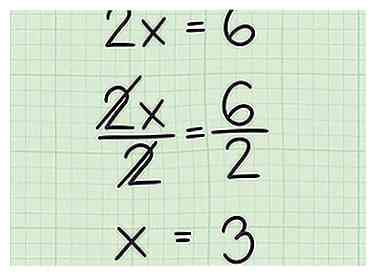 3 Résoudre pour
3 Résoudre pour  4 Écrivez la paire ordonnée. Rappelez-vous qu'une paire ordonnée est écrite sous la forme
4 Écrivez la paire ordonnée. Rappelez-vous qu'une paire ordonnée est écrite sous la forme  1 Déterminer que l'équation de la ligne est une équation quadratique. Une équation quadratique est une équation qui prend la forme
1 Déterminer que l'équation de la ligne est une équation quadratique. Une équation quadratique est une équation qui prend la forme 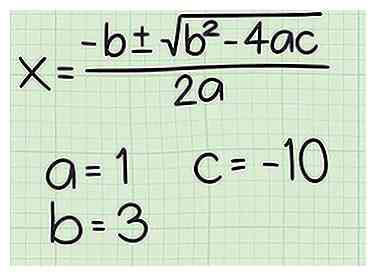 2 Configurez la formule quadratique. La formule est
2 Configurez la formule quadratique. La formule est  3 Branchez toutes les valeurs dans la formule quadratique. Assurez-vous de substituer les valeurs correctes pour chaque variable de l'équation de la ligne.
3 Branchez toutes les valeurs dans la formule quadratique. Assurez-vous de substituer les valeurs correctes pour chaque variable de l'équation de la ligne. 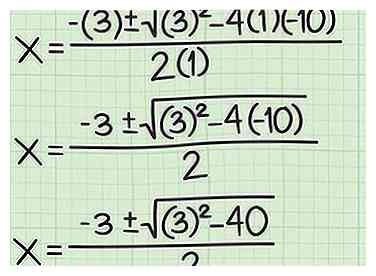 4 Simplifier l'équation. Pour ce faire, complétez d'abord toute la multiplication. Assurez-vous de porter une attention particulière à tous les signes positifs et négatifs.
4 Simplifier l'équation. Pour ce faire, complétez d'abord toute la multiplication. Assurez-vous de porter une attention particulière à tous les signes positifs et négatifs. 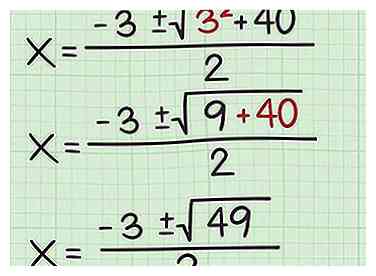 5 Calculez l'exposant. Carré le
5 Calculez l'exposant. Carré le 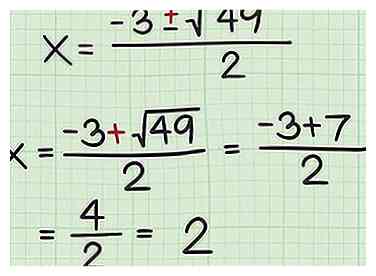 6 Résoudre pour la formule d'addition. Puisque la formule quadratique a un
6 Résoudre pour la formule d'addition. Puisque la formule quadratique a un  7 Résoudre pour la formule de soustraction. Cela vous donnera la deuxième valeur pour
7 Résoudre pour la formule de soustraction. Cela vous donnera la deuxième valeur pour  8 Trouvez les paires ordonnées pour l'ordonnée à l'origine. Rappelez-vous qu'une paire ordonnée donne la coordonnée x en premier, puis la coordonnée y
8 Trouvez les paires ordonnées pour l'ordonnée à l'origine. Rappelez-vous qu'une paire ordonnée donne la coordonnée x en premier, puis la coordonnée y