Un graphique d'une fonction est une représentation visuelle du comportement d'une fonction sur un plan x-y. Les graphiques nous aident à comprendre les différents aspects de la fonction, ce qui serait difficile à comprendre en regardant simplement la fonction elle-même. Vous pouvez tracer des milliers d'équations, et il existe différentes formules pour chacune. Cela dit, il y a toujours moyen de représenter graphiquement une fonction si vous oubliez les étapes exactes pour le type de fonction spécifique.
Méthode One of Three:
Représentation graphique des équations linéaires avec pente
-
 1 Reconnaître les fonctions linéaires comme des lignes simples et faciles à représenter, comme . Il y a une variable et une constante, écrites comme dans une fonction linéaire, sans exposants, radicaux, etc. Si vous avez une équation simple comme celle-ci, alors la représentation graphique de la fonction est facile. Voici d'autres exemples de fonctions linéaires:
1 Reconnaître les fonctions linéaires comme des lignes simples et faciles à représenter, comme . Il y a une variable et une constante, écrites comme dans une fonction linéaire, sans exposants, radicaux, etc. Si vous avez une équation simple comme celle-ci, alors la représentation graphique de la fonction est facile. Voici d'autres exemples de fonctions linéaires: - [1]
-
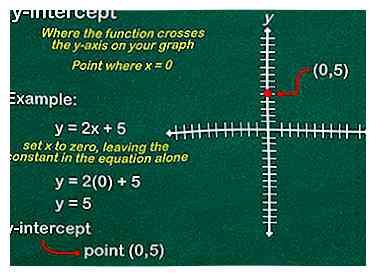 2 Utilisez la constante pour marquer votre ordonnée à l'origine. L'ordonnée à l'origine est l'endroit où la fonction croise l'axe des y sur votre graphique. En d'autres termes, c'est le point où . Donc, pour le trouver, vous définissez simplement x à zéro, laissant la constante dans l'équation seule. Pour l'exemple précédent, , votre ordonnée à l'origine est 5, ou le point (0,5). Sur votre graphique, marquez ce point avec un point.
2 Utilisez la constante pour marquer votre ordonnée à l'origine. L'ordonnée à l'origine est l'endroit où la fonction croise l'axe des y sur votre graphique. En d'autres termes, c'est le point où . Donc, pour le trouver, vous définissez simplement x à zéro, laissant la constante dans l'équation seule. Pour l'exemple précédent, , votre ordonnée à l'origine est 5, ou le point (0,5). Sur votre graphique, marquez ce point avec un point. -
 3 Trouvez la pente de votre ligne avec le numéro juste avant la variable. Dans votre exemple, , la pente est "2" C'est parce que 2 est juste avant la variable dans l'équation, le "x". La pente est la pente de la ligne ou la hauteur de la ligne avant de partir à droite ou à gauche. Les pentes plus grandes signifient des lignes plus raides.
3 Trouvez la pente de votre ligne avec le numéro juste avant la variable. Dans votre exemple, , la pente est "2" C'est parce que 2 est juste avant la variable dans l'équation, le "x". La pente est la pente de la ligne ou la hauteur de la ligne avant de partir à droite ou à gauche. Les pentes plus grandes signifient des lignes plus raides. -
 4 Casser la pente en une fraction. La pente concerne la raideur et l'inclinaison est simplement la différence entre le mouvement de haut en bas et le mouvement à gauche et à droite. La pente est une fraction de montée sur course Combien la ligne "monte" avant de "courir" (va sur le côté)? Pour l'exemple, la pente de "2" pourrait être lue comme .
4 Casser la pente en une fraction. La pente concerne la raideur et l'inclinaison est simplement la différence entre le mouvement de haut en bas et le mouvement à gauche et à droite. La pente est une fraction de montée sur course Combien la ligne "monte" avant de "courir" (va sur le côté)? Pour l'exemple, la pente de "2" pourrait être lue comme . - Si la pente est négative, cela signifie que la ligne descend lorsque vous vous déplacez vers la droite.
-
 5 À partir de votre ordonnée à l'origine, suivez votre "montée" et votre "exécution" pour représenter graphiquement plus de points. Une fois que vous connaissez votre pente, utilisez-la pour tracer votre fonction linéaire. Commencez par votre ordonnée à l'origine, ici (0,5), puis déplacez-vous vers le haut 2, puis 1. Marquez également ce point (1,7). Trouvez 1-2 points supplémentaires pour créer un contour de votre ligne.
5 À partir de votre ordonnée à l'origine, suivez votre "montée" et votre "exécution" pour représenter graphiquement plus de points. Une fois que vous connaissez votre pente, utilisez-la pour tracer votre fonction linéaire. Commencez par votre ordonnée à l'origine, ici (0,5), puis déplacez-vous vers le haut 2, puis 1. Marquez également ce point (1,7). Trouvez 1-2 points supplémentaires pour créer un contour de votre ligne. -
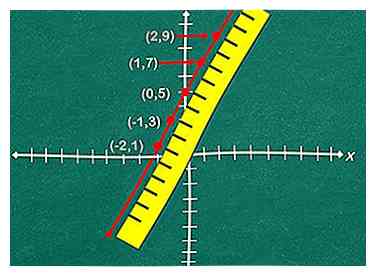 6 Utilisez une règle pour connecter vos points et tracer votre fonction linéaire. Pour éviter les erreurs ou les graphiques approximatifs, trouvez et connectez au moins trois points distincts, bien que deux le fassent à la rigueur. C'est le graphique de votre équation linéaire!
6 Utilisez une règle pour connecter vos points et tracer votre fonction linéaire. Pour éviter les erreurs ou les graphiques approximatifs, trouvez et connectez au moins trois points distincts, bien que deux le fassent à la rigueur. C'est le graphique de votre équation linéaire!
Méthode deux sur trois:
Estimation des points sur un graphique
-
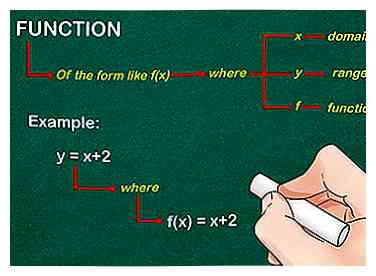 1 Déterminez la fonction. Obtenir la fonction de la forme comme F(X), où y représenterait la gamme, X représenterait le domaine, et F représenterait la fonction. Par exemple, nous utiliserons y = x + 2, où F(X) = x + 2.
1 Déterminez la fonction. Obtenir la fonction de la forme comme F(X), où y représenterait la gamme, X représenterait le domaine, et F représenterait la fonction. Par exemple, nous utiliserons y = x + 2, où F(X) = x + 2. -
 2 Tracez deux lignes dans une forme + sur un morceau de papier. La ligne horizontale est votre X axe. La ligne verticale est votre y axe.
2 Tracez deux lignes dans une forme + sur un morceau de papier. La ligne horizontale est votre X axe. La ligne verticale est votre y axe. -
 3 Numérotez votre graphique. Marquer les deux X l'axe et le y axe avec des nombres équidistants. Pour le X Sur l'axe, les nombres sont positifs à droite et négatifs à gauche. Pour le y Dans l'axe, les nombres sont positifs sur le côté supérieur et négatifs sur le côté inférieur.
3 Numérotez votre graphique. Marquer les deux X l'axe et le y axe avec des nombres équidistants. Pour le X Sur l'axe, les nombres sont positifs à droite et négatifs à gauche. Pour le y Dans l'axe, les nombres sont positifs sur le côté supérieur et négatifs sur le côté inférieur. -
 4 Calculer un y valeur pour 2-3 X valeurs. Prenez votre fonction F(X) = x + 2. Calculer quelques valeurs pour y en mettant les valeurs correspondantes pour X visible sur l'axe dans la fonction. Pour des équations plus complexes, vous pouvez simplifier la fonction en isolant une variable en premier.
4 Calculer un y valeur pour 2-3 X valeurs. Prenez votre fonction F(X) = x + 2. Calculer quelques valeurs pour y en mettant les valeurs correspondantes pour X visible sur l'axe dans la fonction. Pour des équations plus complexes, vous pouvez simplifier la fonction en isolant une variable en premier. - -1: -1 + 2 = 1
- 0: 0 +2 = 2
- 1: 1 + 2 = 3
-
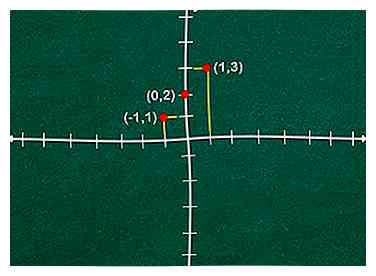 5 Dessine le point graphique pour chaque paire. Esquissez simplement des lignes imaginaires verticalement pour chaque X valeur d'axe et horizontalement pour chaque y valeur de l'axe. Le point d'intersection de ces lignes est un point graphique.
5 Dessine le point graphique pour chaque paire. Esquissez simplement des lignes imaginaires verticalement pour chaque X valeur d'axe et horizontalement pour chaque y valeur de l'axe. Le point d'intersection de ces lignes est un point graphique. -
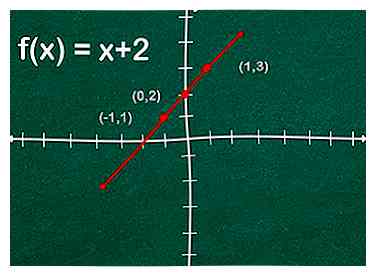 6 Supprimez les lignes imaginaires. Une fois que vous avez dessiné tous les points du graphique, vous pouvez effacer les lignes imaginaires. Note: le graphe de f (x) = x serait une ligne parallèle à celle passant par l'origine (0,0), mais f (x) = x + 2 est décalé de deux unités (le long de l'axe y) sur la grille en raison du +2 dans l'équation.[2]
6 Supprimez les lignes imaginaires. Une fois que vous avez dessiné tous les points du graphique, vous pouvez effacer les lignes imaginaires. Note: le graphe de f (x) = x serait une ligne parallèle à celle passant par l'origine (0,0), mais f (x) = x + 2 est décalé de deux unités (le long de l'axe y) sur la grille en raison du +2 dans l'équation.[2]
Méthode trois sur trois:
Représentation graphique des fonctions complexes à la main
-
 1 Comprendre comment représenter graphiquement les types d'équations communes. Il existe autant de stratégies graphiques différentes que de types de fonctions, beaucoup trop nombreuses pour les couvrir complètement. Si vous éprouvez des difficultés et que les estimations ne marchent pas, consultez les articles sur:
1 Comprendre comment représenter graphiquement les types d'équations communes. Il existe autant de stratégies graphiques différentes que de types de fonctions, beaucoup trop nombreuses pour les couvrir complètement. Si vous éprouvez des difficultés et que les estimations ne marchent pas, consultez les articles sur: - Fonctions quadratiques
- Fonctions rationnelles
- Fonctions logarithmiques
- Inégalités graphiques (pas de fonctions, mais encore des informations utiles).
-
 2 Trouvez les zéros en premier. Les zéros, également appelés x-intercepts, sont les points où le graphique traverse la ligne horizontale du graphique. Bien que tous les graphiques n'aient même pas de zéros, la plupart le font, et c'est la première étape à franchir pour que tout soit sur la bonne voie. Trouver des zéros, simplement la fonction entière à zéro et résoudre. Par exemple:
2 Trouvez les zéros en premier. Les zéros, également appelés x-intercepts, sont les points où le graphique traverse la ligne horizontale du graphique. Bien que tous les graphiques n'aient même pas de zéros, la plupart le font, et c'est la première étape à franchir pour que tout soit sur la bonne voie. Trouver des zéros, simplement la fonction entière à zéro et résoudre. Par exemple: - Définit F (x) égal à zéro:
- Résoudre:
- [3]
-
 3 Trouvez et marquez les asymptotes horizontales ou les endroits où la fonction est impossible, avec une ligne pointillée. Ce sont généralement des points où le graphique n'existe pas, comme lorsque vous divisez par zéro. Si votre équation a une variable dans une fraction, comme , commencez par mettre le bas de la fraction à zéro. Tous les endroits où il est égal à zéro peuvent être séparés par des points (dans cet exemple, une ligne pointillée à x = 2 et x = -2), car vous ne pouvez jamais diviser par zéro. Les fractions, cependant, ne sont pas les seuls endroits où vous pouvez trouver des asymptotes. Généralement, tout ce dont vous avez besoin est du bon sens:
3 Trouvez et marquez les asymptotes horizontales ou les endroits où la fonction est impossible, avec une ligne pointillée. Ce sont généralement des points où le graphique n'existe pas, comme lorsque vous divisez par zéro. Si votre équation a une variable dans une fraction, comme , commencez par mettre le bas de la fraction à zéro. Tous les endroits où il est égal à zéro peuvent être séparés par des points (dans cet exemple, une ligne pointillée à x = 2 et x = -2), car vous ne pouvez jamais diviser par zéro. Les fractions, cependant, ne sont pas les seuls endroits où vous pouvez trouver des asymptotes. Généralement, tout ce dont vous avez besoin est du bon sens: - Certaines fonctions au carré, comme ne peut jamais être négatif. Il y a donc une asymptote à 0.
- Sauf si vous travaillez avec des nombres imaginaires, vous ne pouvez pas avoir [4]
- Pour les équations avec des exposants complexes, vous pouvez avoir de nombreuses asymptotes.
-
 4 Branchez et tracez plusieurs points. Choisissez simplement quelques valeurs pour x et résolvez la fonction. Ensuite, tracez les points sur votre graphique. Plus le graphique est compliqué, plus vous avez besoin de points. En général, -1, 0 et 1 sont les points les plus faciles à obtenir, mais vous aurez besoin de 2 ou 3 de chaque côté du zéro pour obtenir un bon graphique.[5]
4 Branchez et tracez plusieurs points. Choisissez simplement quelques valeurs pour x et résolvez la fonction. Ensuite, tracez les points sur votre graphique. Plus le graphique est compliqué, plus vous avez besoin de points. En général, -1, 0 et 1 sont les points les plus faciles à obtenir, mais vous aurez besoin de 2 ou 3 de chaque côté du zéro pour obtenir un bon graphique.[5] - Pour l'équation , vous pouvez brancher -1,0,1, -2, 2, -10 et 10. Cela vous donne une belle gamme de chiffres à comparer.
- Soyez intelligent en sélectionnant des numéros. Dans l'exemple, vous réaliserez rapidement que le fait d'avoir un signe négatif n'a pas d'importance - vous pouvez arrêter de tester -10, par exemple, car ce sera le même que 10.
-
 5 Mappez le comportement final de la fonction pour voir ce qui se passe quand il est vraiment énorme. Cela vous donne une idée de la direction générale d’une fonction, généralement en tant que verticale asymptote. Par exemple - vous le savez par la suite, devient vraiment très grand. Un seul "x" supplémentaire (un million contre un million et un) rend les choses beaucoup plus grandes. Il existe plusieurs moyens de tester le comportement final, notamment:
5 Mappez le comportement final de la fonction pour voir ce qui se passe quand il est vraiment énorme. Cela vous donne une idée de la direction générale d’une fonction, généralement en tant que verticale asymptote. Par exemple - vous le savez par la suite, devient vraiment très grand. Un seul "x" supplémentaire (un million contre un million et un) rend les choses beaucoup plus grandes. Il existe plusieurs moyens de tester le comportement final, notamment: - Branchez 2-4 grandes valeurs de x, demi-négatif et demi-positif et tracez les points.
- Que se passe-t-il si vous branchez "l'infini" pour une variable? La fonction devient-elle infiniment plus grande ou plus petite?
- Si les degrés sont les mêmes dans une fraction, comme , divisez simplement les deux premiers coefficients ( pour obtenir votre asymptote de fin (-.5).[6]
- Si les degrés sont différents dans une fraction, vous devez diviser l’équation du numérateur par l’équation en dénominateur de la division polynomiale longue.
-
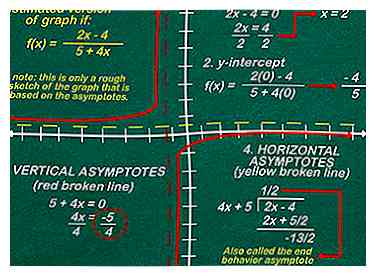 6 Connectez les points, en évitant les asymptotiques et en suivant le comportement final pour représenter graphiquement une estimation de la fonction. Une fois que vous avez 5-6 points, des asymptotes et une idée générale du comportement final, branchez-le pour obtenir une version estimée du graphique.
6 Connectez les points, en évitant les asymptotiques et en suivant le comportement final pour représenter graphiquement une estimation de la fonction. Une fois que vous avez 5-6 points, des asymptotes et une idée générale du comportement final, branchez-le pour obtenir une version estimée du graphique. -
 7 Obtenez des graphiques parfaits en utilisant une calculatrice graphique. Les calculatrices graphiques sont des ordinateurs de poche puissants qui peuvent donner des graphiques exacts pour toute équation. Ils vous permettent de rechercher des points exacts, de trouver des lignes de pente et de visualiser facilement des équations difficiles. Entrez simplement l'équation exacte dans la section graphique (généralement un bouton intitulé "F (x) =") et cliquez sur le graphique pour voir votre fonction au travail.
7 Obtenez des graphiques parfaits en utilisant une calculatrice graphique. Les calculatrices graphiques sont des ordinateurs de poche puissants qui peuvent donner des graphiques exacts pour toute équation. Ils vous permettent de rechercher des points exacts, de trouver des lignes de pente et de visualiser facilement des équations difficiles. Entrez simplement l'équation exacte dans la section graphique (généralement un bouton intitulé "F (x) =") et cliquez sur le graphique pour voir votre fonction au travail.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Reconnaître les fonctions linéaires comme des lignes simples et faciles à représenter, comme
1 Reconnaître les fonctions linéaires comme des lignes simples et faciles à représenter, comme  2 Utilisez la constante pour marquer votre ordonnée à l'origine. L'ordonnée à l'origine est l'endroit où la fonction croise l'axe des y sur votre graphique. En d'autres termes, c'est le point où
2 Utilisez la constante pour marquer votre ordonnée à l'origine. L'ordonnée à l'origine est l'endroit où la fonction croise l'axe des y sur votre graphique. En d'autres termes, c'est le point où  3 Trouvez la pente de votre ligne avec le numéro juste avant la variable. Dans votre exemple,
3 Trouvez la pente de votre ligne avec le numéro juste avant la variable. Dans votre exemple,  4 Casser la pente en une fraction. La pente concerne la raideur et l'inclinaison est simplement la différence entre le mouvement de haut en bas et le mouvement à gauche et à droite. La pente est une fraction de montée sur course Combien la ligne "monte" avant de "courir" (va sur le côté)? Pour l'exemple, la pente de "2" pourrait être lue comme
4 Casser la pente en une fraction. La pente concerne la raideur et l'inclinaison est simplement la différence entre le mouvement de haut en bas et le mouvement à gauche et à droite. La pente est une fraction de montée sur course Combien la ligne "monte" avant de "courir" (va sur le côté)? Pour l'exemple, la pente de "2" pourrait être lue comme  5 À partir de votre ordonnée à l'origine, suivez votre "montée" et votre "exécution" pour représenter graphiquement plus de points. Une fois que vous connaissez votre pente, utilisez-la pour tracer votre fonction linéaire. Commencez par votre ordonnée à l'origine, ici (0,5), puis déplacez-vous vers le haut 2, puis 1. Marquez également ce point (1,7). Trouvez 1-2 points supplémentaires pour créer un contour de votre ligne.
5 À partir de votre ordonnée à l'origine, suivez votre "montée" et votre "exécution" pour représenter graphiquement plus de points. Une fois que vous connaissez votre pente, utilisez-la pour tracer votre fonction linéaire. Commencez par votre ordonnée à l'origine, ici (0,5), puis déplacez-vous vers le haut 2, puis 1. Marquez également ce point (1,7). Trouvez 1-2 points supplémentaires pour créer un contour de votre ligne.  6 Utilisez une règle pour connecter vos points et tracer votre fonction linéaire. Pour éviter les erreurs ou les graphiques approximatifs, trouvez et connectez au moins trois points distincts, bien que deux le fassent à la rigueur. C'est le graphique de votre équation linéaire!
6 Utilisez une règle pour connecter vos points et tracer votre fonction linéaire. Pour éviter les erreurs ou les graphiques approximatifs, trouvez et connectez au moins trois points distincts, bien que deux le fassent à la rigueur. C'est le graphique de votre équation linéaire!  1 Déterminez la fonction. Obtenir la fonction de la forme comme F(X), où y représenterait la gamme, X représenterait le domaine, et F représenterait la fonction. Par exemple, nous utiliserons y = x + 2, où F(X) = x + 2.
1 Déterminez la fonction. Obtenir la fonction de la forme comme F(X), où y représenterait la gamme, X représenterait le domaine, et F représenterait la fonction. Par exemple, nous utiliserons y = x + 2, où F(X) = x + 2.  2 Tracez deux lignes dans une forme + sur un morceau de papier. La ligne horizontale est votre X axe. La ligne verticale est votre y axe.
2 Tracez deux lignes dans une forme + sur un morceau de papier. La ligne horizontale est votre X axe. La ligne verticale est votre y axe.  3 Numérotez votre graphique. Marquer les deux X l'axe et le y axe avec des nombres équidistants. Pour le X Sur l'axe, les nombres sont positifs à droite et négatifs à gauche. Pour le y Dans l'axe, les nombres sont positifs sur le côté supérieur et négatifs sur le côté inférieur.
3 Numérotez votre graphique. Marquer les deux X l'axe et le y axe avec des nombres équidistants. Pour le X Sur l'axe, les nombres sont positifs à droite et négatifs à gauche. Pour le y Dans l'axe, les nombres sont positifs sur le côté supérieur et négatifs sur le côté inférieur.  4 Calculer un y valeur pour 2-3 X valeurs. Prenez votre fonction F(X) = x + 2. Calculer quelques valeurs pour y en mettant les valeurs correspondantes pour X visible sur l'axe dans la fonction. Pour des équations plus complexes, vous pouvez simplifier la fonction en isolant une variable en premier.
4 Calculer un y valeur pour 2-3 X valeurs. Prenez votre fonction F(X) = x + 2. Calculer quelques valeurs pour y en mettant les valeurs correspondantes pour X visible sur l'axe dans la fonction. Pour des équations plus complexes, vous pouvez simplifier la fonction en isolant une variable en premier.  5 Dessine le point graphique pour chaque paire. Esquissez simplement des lignes imaginaires verticalement pour chaque X valeur d'axe et horizontalement pour chaque y valeur de l'axe. Le point d'intersection de ces lignes est un point graphique.
5 Dessine le point graphique pour chaque paire. Esquissez simplement des lignes imaginaires verticalement pour chaque X valeur d'axe et horizontalement pour chaque y valeur de l'axe. Le point d'intersection de ces lignes est un point graphique.  6 Supprimez les lignes imaginaires. Une fois que vous avez dessiné tous les points du graphique, vous pouvez effacer les lignes imaginaires. Note: le graphe de f (x) = x serait une ligne parallèle à celle passant par l'origine (0,0), mais f (x) = x + 2 est décalé de deux unités (le long de l'axe y) sur la grille en raison du +2 dans l'équation.[2]
6 Supprimez les lignes imaginaires. Une fois que vous avez dessiné tous les points du graphique, vous pouvez effacer les lignes imaginaires. Note: le graphe de f (x) = x serait une ligne parallèle à celle passant par l'origine (0,0), mais f (x) = x + 2 est décalé de deux unités (le long de l'axe y) sur la grille en raison du +2 dans l'équation.[2]  1 Comprendre comment représenter graphiquement les types d'équations communes. Il existe autant de stratégies graphiques différentes que de types de fonctions, beaucoup trop nombreuses pour les couvrir complètement. Si vous éprouvez des difficultés et que les estimations ne marchent pas, consultez les articles sur:
1 Comprendre comment représenter graphiquement les types d'équations communes. Il existe autant de stratégies graphiques différentes que de types de fonctions, beaucoup trop nombreuses pour les couvrir complètement. Si vous éprouvez des difficultés et que les estimations ne marchent pas, consultez les articles sur:  2 Trouvez les zéros en premier. Les zéros, également appelés x-intercepts, sont les points où le graphique traverse la ligne horizontale du graphique. Bien que tous les graphiques n'aient même pas de zéros, la plupart le font, et c'est la première étape à franchir pour que tout soit sur la bonne voie. Trouver des zéros, simplement la fonction entière à zéro et résoudre. Par exemple:
2 Trouvez les zéros en premier. Les zéros, également appelés x-intercepts, sont les points où le graphique traverse la ligne horizontale du graphique. Bien que tous les graphiques n'aient même pas de zéros, la plupart le font, et c'est la première étape à franchir pour que tout soit sur la bonne voie. Trouver des zéros, simplement la fonction entière à zéro et résoudre. Par exemple:  3 Trouvez et marquez les asymptotes horizontales ou les endroits où la fonction est impossible, avec une ligne pointillée. Ce sont généralement des points où le graphique n'existe pas, comme lorsque vous divisez par zéro. Si votre équation a une variable dans une fraction, comme
3 Trouvez et marquez les asymptotes horizontales ou les endroits où la fonction est impossible, avec une ligne pointillée. Ce sont généralement des points où le graphique n'existe pas, comme lorsque vous divisez par zéro. Si votre équation a une variable dans une fraction, comme  4 Branchez et tracez plusieurs points. Choisissez simplement quelques valeurs pour x et résolvez la fonction. Ensuite, tracez les points sur votre graphique. Plus le graphique est compliqué, plus vous avez besoin de points. En général, -1, 0 et 1 sont les points les plus faciles à obtenir, mais vous aurez besoin de 2 ou 3 de chaque côté du zéro pour obtenir un bon graphique.[5]
4 Branchez et tracez plusieurs points. Choisissez simplement quelques valeurs pour x et résolvez la fonction. Ensuite, tracez les points sur votre graphique. Plus le graphique est compliqué, plus vous avez besoin de points. En général, -1, 0 et 1 sont les points les plus faciles à obtenir, mais vous aurez besoin de 2 ou 3 de chaque côté du zéro pour obtenir un bon graphique.[5]  5 Mappez le comportement final de la fonction pour voir ce qui se passe quand il est vraiment énorme. Cela vous donne une idée de la direction générale d’une fonction, généralement en tant que verticale asymptote. Par exemple - vous le savez par la suite,
5 Mappez le comportement final de la fonction pour voir ce qui se passe quand il est vraiment énorme. Cela vous donne une idée de la direction générale d’une fonction, généralement en tant que verticale asymptote. Par exemple - vous le savez par la suite,  6 Connectez les points, en évitant les asymptotiques et en suivant le comportement final pour représenter graphiquement une estimation de la fonction. Une fois que vous avez 5-6 points, des asymptotes et une idée générale du comportement final, branchez-le pour obtenir une version estimée du graphique.
6 Connectez les points, en évitant les asymptotiques et en suivant le comportement final pour représenter graphiquement une estimation de la fonction. Une fois que vous avez 5-6 points, des asymptotes et une idée générale du comportement final, branchez-le pour obtenir une version estimée du graphique.  7 Obtenez des graphiques parfaits en utilisant une calculatrice graphique. Les calculatrices graphiques sont des ordinateurs de poche puissants qui peuvent donner des graphiques exacts pour toute équation. Ils vous permettent de rechercher des points exacts, de trouver des lignes de pente et de visualiser facilement des équations difficiles. Entrez simplement l'équation exacte dans la section graphique (généralement un bouton intitulé "F (x) =") et cliquez sur le graphique pour voir votre fonction au travail.
7 Obtenez des graphiques parfaits en utilisant une calculatrice graphique. Les calculatrices graphiques sont des ordinateurs de poche puissants qui peuvent donner des graphiques exacts pour toute équation. Ils vous permettent de rechercher des points exacts, de trouver des lignes de pente et de visualiser facilement des équations difficiles. Entrez simplement l'équation exacte dans la section graphique (généralement un bouton intitulé "F (x) =") et cliquez sur le graphique pour voir votre fonction au travail.