Comment représenter graphiquement les inégalités

Vous pouvez représenter graphiquement une inégalité linéaire ou quadratique de la même manière que vous grapheriez une équation. La différence est que, comme une inégalité montre un ensemble de valeurs supérieur ou inférieur à, votre graphique affichera plus qu'un simple point sur une droite numérique ou une ligne sur un plan de coordonnées. En utilisant l'algèbre et en évaluant le signe d'inégalité, vous pouvez déterminer quelles valeurs sont incluses dans la solution d'une inégalité.

Méthode One of Three:
Représentation graphique d'une inégalité linéaire sur une droite numérique

1. 1 Résoudre pour la variable. Pour résoudre l'inégalité, isolez la variable en utilisant les mêmes méthodes algébriques que vous utiliseriez pour résoudre une équation.^[1] Rappelez-vous que lorsque vous multipliez ou divisez par un nombre négatif, vous devez retourner le signe d'inégalité.
   • Par exemple, si vous résolvez l'inégalité $\ displaystyle 3y + 9> 12$, isoler la variable en soustrayant 9 de chaque côté de l’inégalité, puis en divisant par 3:
     $\ displaystyle 3y + 9> 12$
     $\ displaystyle 3y + 9-9> 12-9$
     $\ displaystyle 3y> 3$
     $\ displaystyle \ frac 3y 3> \ frac 3 3$
     $\ displaystyle y> 1$
   • Votre inégalité ne devrait avoir qu'une seule variable. Si votre inégalité a deux variables, il est préférable de la représenter graphiquement sur un plan de coordonnées en utilisant une autre méthode.
2. 2 Tracez une droite numérique. Incluez la valeur relative sur votre droite numérique (la valeur que vous avez trouvée inférieure, supérieure ou égale à). Faites la ligne de chiffres aussi longue ou courte que nécessaire.
   • Par exemple, si vous avez trouvé que $\ displaystyle y> 1$, assurez-vous d'inclure un point pour 1 sur la droite numérique.
3. 3 Tracez un cercle indiquant la valeur relative. Si la valeur est inférieure à ($\ displaystyle <$) ou supérieur à ($\ displaystyle>$) ce nombre, le cercle doit être ouvert, car la solution n'inclut pas la valeur. Si la valeur est inférieure ou égale à ($\ displaystyle \ leq$), ou supérieur ou égal à ($\ displaystyle \ geq$), le cercle doit être rempli, car la solution inclut la valeur.^[2]
   • Par exemple, si $\ displaystyle y> 1$, vous tracez un cercle à 1 sur la droite numérique. Vous ne remplissez pas le cercle, car 1 n'est pas inclus dans la solution.
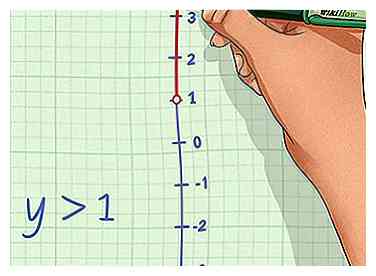4. 4 Tracez une flèche indiquant les valeurs incluses. Si la variable est supérieure à la valeur relative, votre flèche doit pointer vers la droite, car la solution inclut des valeurs supérieures à ce nombre. Si la variable est inférieure à la valeur relative, votre flèche doit pointer vers la gauche, car la solution inclut des valeurs inférieures à ce nombre.^[3]
   • Par exemple, pour la solution $\ displaystyle y> 1$, vous dessinez une flèche pointant vers la droite, car la solution inclut des valeurs supérieures à 1.

Méthode deux sur trois:
Représentation graphique d'une inégalité linéaire dans un plan de coordonnées

1. 1 Résoudre pour $\ displaystyle y$. Vous voulez trouver l’équation de la ligne, pour ce faire vous devez isoler le $\ displaystyle y$ variable sur le côté gauche de l'équation en utilisant l'algèbre.^[4] Le côté droit de l’équation devrait avoir le $\ displaystyle x$ variable, et probablement, une constante.
   • Par exemple, pour l'inégalité $\ displaystyle 3y + 9> 9x$, vous isoleriez la variable y en soustrayant 9 des deux côtés, puis en divisant par 3:
     $\ displaystyle 3y + 9> 9x$
     $\ displaystyle 3y + 9-9> 9x-9$
     $\ displaystyle 3y> 9x-9$
     $\ displaystyle \ frac 3y 3> \ frac 9x-9 3$
     $\ displaystyle y> 3x-3$
2. 2 Graphique la ligne sur un plan de coordonnées. Pour ce faire, transformez l'inégalité en une équation et créez un graphique comme vous le feriez pour n'importe quelle équation d'une ligne.^[5] Tracez l'ordonnée à l'origine, puis utilisez la pente pour tracer les autres points de la ligne.
   • Par exemple, si l'inégalité est $\ displaystyle y> 3x-3$, vous grapheriez la ligne $\ displaystyle y = 3x-3$. L'ordonnée à l'origine (le point où la ligne traverse l'axe des y) est -3 et la pente est égale à 3, ou $\ displaystyle \ frac 3 1$. Donc, vous tireriez un point à $\ displaystyle (0, -3)$. Le point au-dessus de l'ordonnée à l'origine est $\ displaystyle (1,0)$. Le point en dessous de l'ordonnée à l'origine est $\ displaystyle (-1, -6)$.
3. 3 Dessiner la ligne. Si l'inégalité est inférieure à ($\ displaystyle <$) ou supérieur à ($\ displaystyle>$), la ligne doit être tiretée, car la solution n'inclut pas de valeurs égales à la ligne. Si la valeur est inférieure ou égale à ($\ displaystyle \ leq$), ou supérieur ou égal à ($\ displaystyle \ geq$), la ligne doit être solide, car la solution inclut des valeurs égales à la ligne.^[6]
   • Par exemple, puisque l'inégalité est $\ displaystyle y> 3x-3$, la ligne doit être tiretée, car les valeurs n'incluent pas de points sur la ligne.
4. 4 Ombre dans la zone appropriée. Si l'inégalité montre $\ displaystyle y> mx + b$ vous devriez faire de l'ombre dans la zone au-dessus de la ligne. Si l'inégalité montre $\ displaystyle y<>$, vous devez ombrer la zone en dessous de la ligne.^[7]
   • Par exemple, pour l'inégalité $\ displaystyle y> 3x-3$ vous feriez de l'ombre au-dessus de la ligne.

Méthode trois sur trois:
Représentation graphique d'une inégalité quadratique sur un plan de coordonnées

1. 1 Déterminez si vous avez une inégalité quadratique. Une inégalité quadratique prend la forme de $\ displaystyle ax ^ 2 + bx + c$.^[8] Parfois, il peut ne pas y avoir de $\ displaystyle x$ terme ou une constante, mais il devrait toujours y avoir un $\ displaystyle x ^ 2$ terme d'un côté de l'inégalité, et un isolé $\ displaystyle y$ variable de l'autre côté.
   • Par exemple, vous pourriez avoir besoin de représenter graphiquement l'inégalité $\ displaystyle y<>$.
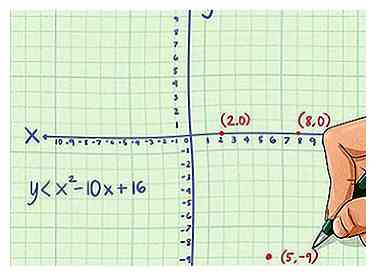2. 2 Graphique la ligne sur un plan de coordonnées. Pour ce faire, transformez l'inégalité en une équation et tracez la ligne comme vous le feriez normalement. Comme vous avez une équation quadratique, la ligne sera une parabole.^[9]
   • Par exemple, pour l'inégalité $\ displaystyle y<>$, vous grapheriez la ligne $\ displaystyle y = x ^ 2 -10x + 16$. Le sommet est au point $\ displaystyle (5, -9)$, et la parabole traverse l'axe des x aux points $\ displaystyle (2,0)$ et $\ displaystyle (8,0)$.
3. 3 Dessine la parabole. Dessine la parabole avec une ligne pointillée si l'inégalité est inférieure à ($\ displaystyle <$) ou supérieur à ($\ displaystyle>$). Si la valeur est inférieure ou égale à ($\ displaystyle \ leq$), ou supérieur ou égal à ($\ displaystyle \ geq$), vous devez dessiner la parabole avec un trait plein, car la solution comprend des valeurs égales à la ligne.
   • Par exemple, pour l'inégalité $\ displaystyle y<>$, vous dessinez la parabole avec une ligne pointillée.
4. 4 Trouvez des points de test. Pour déterminer la zone à ombrer, vous devez choisir des points à l'intérieur de la parabole et à l'extérieur de la parabole.
   • Par exemple, le graphique de l'inégalité $\ displaystyle y<>$ montre que le point $\ displaystyle (0,0)$ est en dehors de la parabole. Ce serait un bon point pour tester la solution.
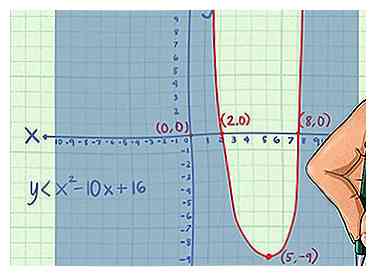5. 5 Ombrez la zone appropriée. Pour déterminer la zone à ombrer, branchez les valeurs de $\ displaystyle x$ et $\ displaystyle y$ de vos points de test dans l'inégalité d'origine. Le point qui produit une inégalité réelle indique quelle zone du graphique doit être ombrée.^[10]
   • Par exemple, brancher les valeurs de $\ displaystyle x$ et $\ displaystyle y$ du point $\ displaystyle (0,0)$ dans l'inégalité d'origine, vous obtenez:
     $\ displaystyle y<>$
     $\ displaystyle 0 <0 ^ 2 -0x + 16$
     $\ displaystyle 0 <16$
     Comme cela est vrai, vous nuanceriez la zone du graphique où le point $\ displaystyle (0,0)$ est trouvé. Dans ce cas, c'est en dehors de la parabole, pas à l'intérieur de celle-ci.