Les binômes sont de petites expressions mathématiques constituées d'un terme variable (x, a, 3x, 4t, 1090y) ajouté ou soustrait par un terme constant (1, 3, 110, etc.). Binômes toujours contiennent seulement deux termes, mais ils sont les blocs de construction de beaucoup plus grandes et plus complexes équations appelées polynômes, ce qui les rend extrêmement important de bien apprendre. Cette leçon couvrira plusieurs types de multiplication binomiale, mais ils peuvent tous être appris séparément.
Méthode One of Three:
Multiplication de deux binômes
-
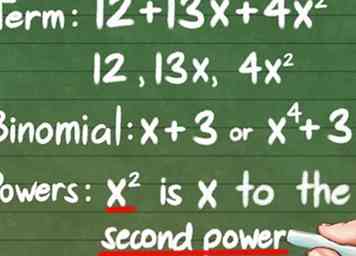 1 Comprendre le vocabulaire mathématique et les types de questions. Il sera impossible de résoudre les questions lors de votre prochain test si vous ne savez pas ce qu’elles demandent. Heureusement, la terminologie n'est pas incroyablement difficile:
1 Comprendre le vocabulaire mathématique et les types de questions. Il sera impossible de résoudre les questions lors de votre prochain test si vous ne savez pas ce qu’elles demandent. Heureusement, la terminologie n'est pas incroyablement difficile: - Termes: Un terme est simplement une partie de l'équation ajoutée ou soustraite. Cela peut être une constante, une variable ou les deux. Par exemple, en 12 + 13x + 4x2, les termes sont 12, 13x, et 4x2.
- Binôme: Ceci est juste une manière compliquée de dire "une expression avec deux termes", comme x + 3 ou X4 - 3x.
- Pouvoirs: cela fait référence à un exposant sur un terme. Par exemple, on pourrait dire que x2 est "x à la deuxième puissance."
- Pour toute question vous demandant de « trouver les termes de deux binômes (x + 3) (x + 2) », « trouver le produit de deux binômes » ou « compléter les deux binômes » vous demande de multiplier les binômes.
-
 2 Apprenez l’acronyme FOIL pour vous rappeler l’ordre de multiplication binomiale. FOIL est un guide simple pour multiplier deux binômes. FOIL signifie la commande dont vous avez besoin pour multiplier les parties des binômes: F pour Premier, O est pour Extérieur, Je suis pour Interne, et L est pour Dernier. Les noms font référence à l'ordre dans lequel les termes sont écrits. Disons que nous multiplions les binômes (x + 2) et (x + 5). Les termes seraient:
2 Apprenez l’acronyme FOIL pour vous rappeler l’ordre de multiplication binomiale. FOIL est un guide simple pour multiplier deux binômes. FOIL signifie la commande dont vous avez besoin pour multiplier les parties des binômes: F pour Premier, O est pour Extérieur, Je suis pour Interne, et L est pour Dernier. Les noms font référence à l'ordre dans lequel les termes sont écrits. Disons que nous multiplions les binômes (x + 2) et (x + 5). Les termes seraient: - Premier: x & x
- Extérieur: x et 5
- Interne: 2 & x
- Dernier: 2 & 5
-
 3 Multipliez la première partie de chaque parenthèse. C'est le "F" de FOIL. Dans notre exemple, (x + 2) (x + 5), les premiers termes sont "x" et "x". Multipliez-les ensemble et notez la réponse: "x2."
3 Multipliez la première partie de chaque parenthèse. C'est le "F" de FOIL. Dans notre exemple, (x + 2) (x + 5), les premiers termes sont "x" et "x". Multipliez-les ensemble et notez la réponse: "x2." - Premier mandat: x * x = x2
-
 4 Multipliez les parties OUTER dans chaque parenthèse. Ce sont deux «extrémités» extérieures à notre problème. Donc, dans notre exemple (x + 2) (x + 5), ils seraient "x" et "5." Ensemble ils font "5x"
4 Multipliez les parties OUTER dans chaque parenthèse. Ce sont deux «extrémités» extérieures à notre problème. Donc, dans notre exemple (x + 2) (x + 5), ils seraient "x" et "5." Ensemble ils font "5x" - Terme externe: x * 5 = 5x
-
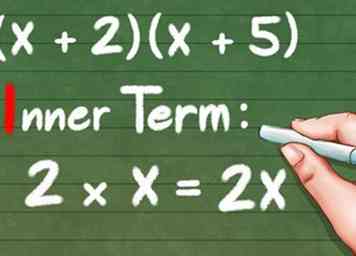 5 Multipliez les parties INNER dans chaque parenthèse. Les deux nombres les plus proches du centre seront votre terme interne. Pour (x + 2) (x + 5), cela signifie que vous multipliez "2" et "x" pour obtenir "2x".
5 Multipliez les parties INNER dans chaque parenthèse. Les deux nombres les plus proches du centre seront votre terme interne. Pour (x + 2) (x + 5), cela signifie que vous multipliez "2" et "x" pour obtenir "2x". - Terme interne: 2 * x = 2x
-
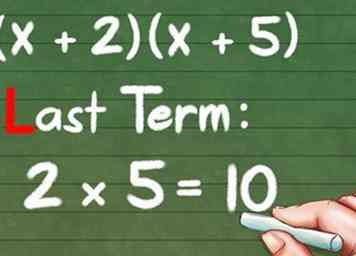 6 Multipliez les dernières parties de chaque parenthèse. Cela fait ne pas signifie les deux derniers chiffres, mais plutôt le dernier nombre entre parenthèses. Donc, pour (x + 2) (x + 5), nous multiplions le "2" et le "5" pour obtenir "10."
6 Multipliez les dernières parties de chaque parenthèse. Cela fait ne pas signifie les deux derniers chiffres, mais plutôt le dernier nombre entre parenthèses. Donc, pour (x + 2) (x + 5), nous multiplions le "2" et le "5" pour obtenir "10." - Dernier terme: 2 * 5 = 10
-
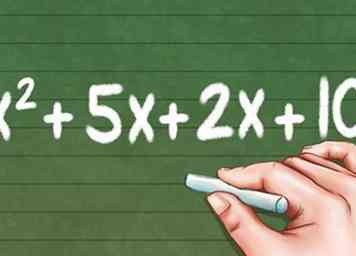 7 Ajoutez tous les nouveaux termes ensemble. Combinez les termes en les ajoutant ensemble pour créer une nouvelle expression plus grande. De notre exemple précédent, nous obtenons l'équation:
7 Ajoutez tous les nouveaux termes ensemble. Combinez les termes en les ajoutant ensemble pour créer une nouvelle expression plus grande. De notre exemple précédent, nous obtenons l'équation: - X2 + 5x + 2x + 10
-
 8 Simplifiez les termes similaires. Les termes similaires sont des parties de l'équation qui ont la même variable et le même pouvoir. Dans notre exemple, les termes 2x et 5x partagent tous deux un x et peuvent être ajoutés ensemble. Aucun autre terme ne se ressemble, alors ils restent.
8 Simplifiez les termes similaires. Les termes similaires sont des parties de l'équation qui ont la même variable et le même pouvoir. Dans notre exemple, les termes 2x et 5x partagent tous deux un x et peuvent être ajoutés ensemble. Aucun autre terme ne se ressemble, alors ils restent. - Réponse finale: (x + 2) (x + 5) = X2 + 7x + 10
- Remarque avancée: Pour apprendre comment fonctionnent les termes, rappelez-vous les bases de la multiplication. 3 * 5, par exemple, signifie que vous ajoutez trois fois cinq pour obtenir 15 (5 + 5 + 5). Dans notre équation, nous avons 5 * x (x + x + x + x + x) et 2 * x (x + x). Si nous ajoutons tous les "x" dans l'équation, nous obtenons sept "x" ou 7x.
-
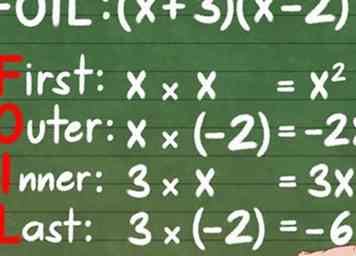 9 Rappelez-vous que les nombres soustraits sont négatifs. Lorsqu'un nombre est soustrait, cela revient à ajouter un nombre négatif. Si vous oubliez de garder le signe moins tout au long de vos calculs, vous vous retrouverez avec la mauvaise réponse. Prenons l'exemple (x + 3) (x-2):
9 Rappelez-vous que les nombres soustraits sont négatifs. Lorsqu'un nombre est soustrait, cela revient à ajouter un nombre négatif. Si vous oubliez de garder le signe moins tout au long de vos calculs, vous vous retrouverez avec la mauvaise réponse. Prenons l'exemple (x + 3) (x-2): - Premier: x * x = x2
- Extérieur: x * -2 = -2x
- Interne: 3 * x = 3x
- Dernier: 3 * -2 = -6
- Ajouter tous les termes ensemble: X2 - 2x + 3x - 6
- Simplifiez la réponse finale: X2 + x - 6
Méthode deux sur trois:
Multiplier plus de deux binômes
-
 1 Multipliez les deux premiers binômes en ignorant temporairement le troisième. Prenons l'exemple (x + 4) (x + 1) (x + 3). Nous devons multiplier les binômes un par un, donc multipliez les deux par FOIL ou par distribution de termes. Multiplier les deux premiers (x + 4) et (x + 1) par FOIL ressemblerait à ceci:
1 Multipliez les deux premiers binômes en ignorant temporairement le troisième. Prenons l'exemple (x + 4) (x + 1) (x + 3). Nous devons multiplier les binômes un par un, donc multipliez les deux par FOIL ou par distribution de termes. Multiplier les deux premiers (x + 4) et (x + 1) par FOIL ressemblerait à ceci: - Premier: x * x = x2
- Extérieur: 1 * x = x
- Interne: 4 * x = 4x
- Dernier: 1*4 = 4
- Combinez les termes: X2 + x + 4x + 4
- (x + 4) (x + 1) = X2 + 5x +4
-
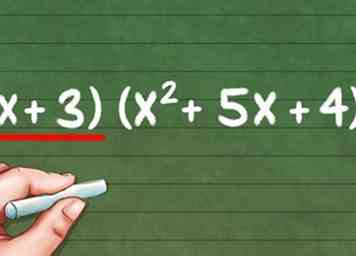 2 Combinez le binôme restant avec votre nouvelle équation. Maintenant que cette partie de l'équation a été multipliée, vous pouvez gérer le binôme restant. Dans l'exemple, (x + 4) (x + 1) (x + 3), le terme de surplus est (x + 3). Remettez-le avec la nouvelle équation, vous donnant: (x + 3) (x2 + 5x + 4).
2 Combinez le binôme restant avec votre nouvelle équation. Maintenant que cette partie de l'équation a été multipliée, vous pouvez gérer le binôme restant. Dans l'exemple, (x + 4) (x + 1) (x + 3), le terme de surplus est (x + 3). Remettez-le avec la nouvelle équation, vous donnant: (x + 3) (x2 + 5x + 4). -
 3 Multipliez le premier nombre du binôme par les trois nombres entre parenthèses. C'est la distribution des termes. Donc, pour l'équation (x + 3) (x2 + 5x + 4), vous devez multiplier le premier x par les trois parties de la deuxième parenthèse, "x2, "" 5x "et" 4. "
3 Multipliez le premier nombre du binôme par les trois nombres entre parenthèses. C'est la distribution des termes. Donc, pour l'équation (x + 3) (x2 + 5x + 4), vous devez multiplier le premier x par les trois parties de la deuxième parenthèse, "x2, "" 5x "et" 4. " - (x * x2) + (x * 5x) + (x * 4) = X3 + 5x2 + 4x
- Ecrivez cette réponse et enregistrez-la pour plus tard.
-
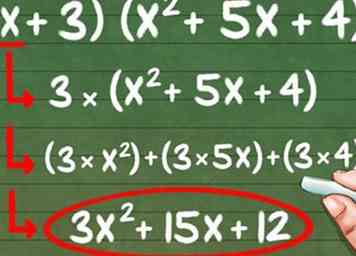 4 Multipliez le deuxième nombre dans le binôme par les trois nombres entre parenthèses. Prenez l'équation (x + 3) (x2 + 5x + 4). Maintenant, multipliez la deuxième partie du binôme par les trois parties entre parenthèses, "x2, "" 5x "et" 4. "
4 Multipliez le deuxième nombre dans le binôme par les trois nombres entre parenthèses. Prenez l'équation (x + 3) (x2 + 5x + 4). Maintenant, multipliez la deuxième partie du binôme par les trois parties entre parenthèses, "x2, "" 5x "et" 4. " - (3 * x2) + (3 * 5x) + (3 * 4) = 3x2 + 15x + 12
- Ecrivez cette réponse à côté de la première réponse.
-
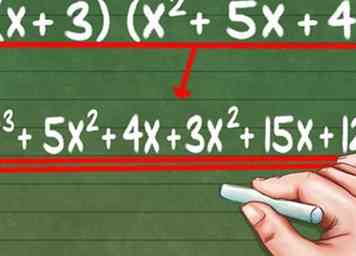 5 Additionnez les deux réponses de la multiplication. Vous devez combiner les réponses des deux étapes précédentes, car elles constituent les deux parties de votre réponse finale.
5 Additionnez les deux réponses de la multiplication. Vous devez combiner les réponses des deux étapes précédentes, car elles constituent les deux parties de votre réponse finale. - X3 + 5x2 + 4x + 3x2 + 15x + 12
-
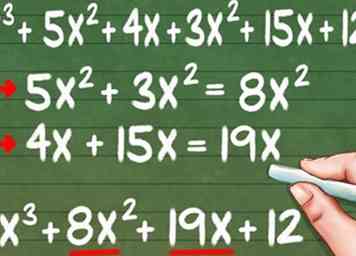 6 Simplifiez l'équation pour obtenir votre réponse finale. Tous les termes "similaires", termes qui partagent la même variable et la même puissance (comme 5x2 et 3x2), peuvent être ajoutés pour rendre votre réponse plus simple.
6 Simplifiez l'équation pour obtenir votre réponse finale. Tous les termes "similaires", termes qui partagent la même variable et la même puissance (comme 5x2 et 3x2), peuvent être ajoutés pour rendre votre réponse plus simple. - 5x2 et 3x2 devenir 8x2
- 4x et 15x deviennent 19x
- (x + 4) (x + 1) (x + 3) = X3 + 8x2 + 19x + 12
-
 7 Toujours utiliser la distribution pour résoudre les problèmes de multiplication plus importants. Comme vous pouvez utiliser la distribution de termes pour multiplier des équations de n'importe quelle longueur, vous disposez désormais des outils nécessaires pour résoudre des problèmes plus importants, tels que (x + 1) (x + 2) (x + 3). Multipliez deux binômes en utilisant soit la distribution des termes ou FOIL, puis utilisez la distribution des termes pour multiplier le binôme final aux deux premiers. Dans l'exemple suivant, nous FOIL (x + 1) (x + 2), puis distribuons les termes avec (x + 3) pour obtenir la réponse finale:
7 Toujours utiliser la distribution pour résoudre les problèmes de multiplication plus importants. Comme vous pouvez utiliser la distribution de termes pour multiplier des équations de n'importe quelle longueur, vous disposez désormais des outils nécessaires pour résoudre des problèmes plus importants, tels que (x + 1) (x + 2) (x + 3). Multipliez deux binômes en utilisant soit la distribution des termes ou FOIL, puis utilisez la distribution des termes pour multiplier le binôme final aux deux premiers. Dans l'exemple suivant, nous FOIL (x + 1) (x + 2), puis distribuons les termes avec (x + 3) pour obtenir la réponse finale: - (x + 1) (x + 2) (x + 3) = (x + 1) (x + 2) * (x + 3)
- (x + 1) (x + 2) = x2 + 3x + 2
- (x + 1) (x + 2) (x + 3) = (x2 + 3: + 2) * (x + 3)
- (X2 + 3x + 2) * (x + 3) = x3 + 3x2 + 2x + 3x2 + 9x + 6
- Simplifiez la réponse finale: X3 + 6x2 + 11x + 6
Méthode trois sur trois:
Quadrillage binôme
-
 1 Savoir mettre en place "des formules générales."Les formules générales vous permettent de brancher simplement vos chiffres au lieu de calculer FOIL à chaque fois. Des binômes qui sont portés à la deuxième puissance, comme (x + 2)2, ou le troisième pouvoir, comme (4y + 12)3, peut être facilement adapté à une formule préexistante, ce qui rend la résolution rapide et facile. Pour trouver la formule générale, nous remplaçons tous les nombres par des variables. Ensuite, à la fin, nous pouvons relancer nos chiffres pour obtenir notre réponse. Commencez avec l'équation (a + b)2, où:
1 Savoir mettre en place "des formules générales."Les formules générales vous permettent de brancher simplement vos chiffres au lieu de calculer FOIL à chaque fois. Des binômes qui sont portés à la deuxième puissance, comme (x + 2)2, ou le troisième pouvoir, comme (4y + 12)3, peut être facilement adapté à une formule préexistante, ce qui rend la résolution rapide et facile. Pour trouver la formule générale, nous remplaçons tous les nombres par des variables. Ensuite, à la fin, nous pouvons relancer nos chiffres pour obtenir notre réponse. Commencez avec l'équation (a + b)2, où: - une représente le terme variable (c.-à-d. 4 ans - 1, 2x2 + 3, etc.) S'il n'y a pas de nombre, alors a = 1, puisque 1 * x = x.
- b représente la constante ajoutée ou soustraite (c.-à-d. x + 10, t - 12).
-
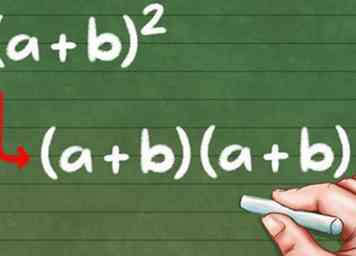 2 Sachez que les binômes carrés peuvent être réécrits. (a + b)2 peut sembler plus compliqué que notre exemple précédent, mais rappelez-vous que la quadrature d'un nombre ne fait que le multiplier par lui-même. Ainsi, nous pouvons réécrire l’équation pour la rendre plus familière:
2 Sachez que les binômes carrés peuvent être réécrits. (a + b)2 peut sembler plus compliqué que notre exemple précédent, mais rappelez-vous que la quadrature d'un nombre ne fait que le multiplier par lui-même. Ainsi, nous pouvons réécrire l’équation pour la rendre plus familière: - (a + b)2 = (a + b) (a + b)
-
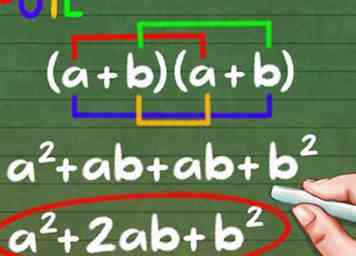 3 Utilisez FOIL pour résoudre la nouvelle équation. Si nous utilisons foil sur cette équation, nous aurons une formule générale qui ressemble à la solution à toute multiplication binomiale. Rappelez-vous que dans la multiplication, l'ordre que vous multipliez n'a pas d'importance
3 Utilisez FOIL pour résoudre la nouvelle équation. Si nous utilisons foil sur cette équation, nous aurons une formule générale qui ressemble à la solution à toute multiplication binomiale. Rappelez-vous que dans la multiplication, l'ordre que vous multipliez n'a pas d'importance - Réécrire comme (a + b) (a + b).
- Premier: a * a = a2
- Interne: b * a = ba
- Extérieur: a * b = ab
- Dernier: b * b = b2.
- Ajouter les nouveaux termes: une2 + ba + ab + b2
- Combinez comme termes: une2 + 2ab + b2
- Remarque avancée: Les exposants et les radicaux sont considérés comme des opérations hyper 3, alors que la multiplication et la division sont hyper 2. Cela signifie que les propriétés de multiplication et de division ne fonctionnent pas pour les exposants. (a + b)2 n'est pas égal à un2 + b2. C'est une erreur très courante chez les gens.
-
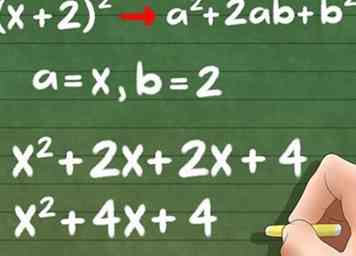 4 Utilisez l'équation générale a2 + 2ab + b2 pour résoudre vos problèmes. Prenons l'équation (x + 2)2. Au lieu de refaire le FOIL, nous pouvons insérer le premier terme pour "a" et le second terme pour "b",
4 Utilisez l'équation générale a2 + 2ab + b2 pour résoudre vos problèmes. Prenons l'équation (x + 2)2. Au lieu de refaire le FOIL, nous pouvons insérer le premier terme pour "a" et le second terme pour "b", - Équation générale: a2 + 2ab + b2
- a = x, b = 2
- X2 + (2 * x * 2) + 22
- Réponse finale: X2 + 4x + 4.
- Vous pouvez toujours vérifier votre travail en effectuant FOIL sur l'équation d'origine, (x + 2) (x + 2). Vous obtiendrez la même réponse à chaque fois si cela est fait correctement.
- Si un terme est soustrait, vous devez toujours le garder négatif dans l’équation générale.
-
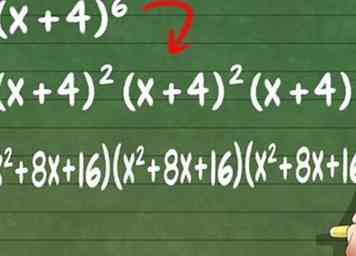 5 N'oubliez pas d'insérer le terme entier dans l'équation générale. Vu le binôme (2x + 3)2, vous devez vous rappeler que a = 2x, pas simplement a = 2. Lorsque vous avez des termes complexes, vous devez vous rappeler que les 2 et les x sont au carré.
5 N'oubliez pas d'insérer le terme entier dans l'équation générale. Vu le binôme (2x + 3)2, vous devez vous rappeler que a = 2x, pas simplement a = 2. Lorsque vous avez des termes complexes, vous devez vous rappeler que les 2 et les x sont au carré. - Équation générale: a2 + 2ab + b2
- Substitut pour a et b: (2x)2 + 2 (2x) (3) + 32
- Carré chaque terme: (22)(X2) + 14x + 32
- Simplifiez la réponse finale: 4x2 + 14x + 9
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
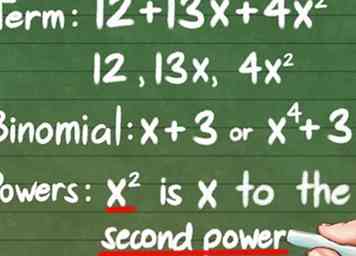 1 Comprendre le vocabulaire mathématique et les types de questions. Il sera impossible de résoudre les questions lors de votre prochain test si vous ne savez pas ce qu’elles demandent. Heureusement, la terminologie n'est pas incroyablement difficile:
1 Comprendre le vocabulaire mathématique et les types de questions. Il sera impossible de résoudre les questions lors de votre prochain test si vous ne savez pas ce qu’elles demandent. Heureusement, la terminologie n'est pas incroyablement difficile:  2 Apprenez l’acronyme FOIL pour vous rappeler l’ordre de multiplication binomiale. FOIL est un guide simple pour multiplier deux binômes. FOIL signifie la commande dont vous avez besoin pour multiplier les parties des binômes: F pour Premier, O est pour Extérieur, Je suis pour Interne, et L est pour Dernier. Les noms font référence à l'ordre dans lequel les termes sont écrits. Disons que nous multiplions les binômes (x + 2) et (x + 5). Les termes seraient:
2 Apprenez l’acronyme FOIL pour vous rappeler l’ordre de multiplication binomiale. FOIL est un guide simple pour multiplier deux binômes. FOIL signifie la commande dont vous avez besoin pour multiplier les parties des binômes: F pour Premier, O est pour Extérieur, Je suis pour Interne, et L est pour Dernier. Les noms font référence à l'ordre dans lequel les termes sont écrits. Disons que nous multiplions les binômes (x + 2) et (x + 5). Les termes seraient:  3 Multipliez la première partie de chaque parenthèse. C'est le "F" de FOIL. Dans notre exemple, (x + 2) (x + 5), les premiers termes sont "x" et "x". Multipliez-les ensemble et notez la réponse: "x2."
3 Multipliez la première partie de chaque parenthèse. C'est le "F" de FOIL. Dans notre exemple, (x + 2) (x + 5), les premiers termes sont "x" et "x". Multipliez-les ensemble et notez la réponse: "x2."  4 Multipliez les parties OUTER dans chaque parenthèse. Ce sont deux «extrémités» extérieures à notre problème. Donc, dans notre exemple (x + 2) (x + 5), ils seraient "x" et "5." Ensemble ils font "5x"
4 Multipliez les parties OUTER dans chaque parenthèse. Ce sont deux «extrémités» extérieures à notre problème. Donc, dans notre exemple (x + 2) (x + 5), ils seraient "x" et "5." Ensemble ils font "5x" 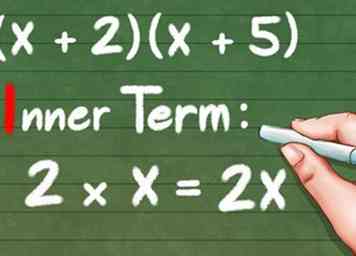 5 Multipliez les parties INNER dans chaque parenthèse. Les deux nombres les plus proches du centre seront votre terme interne. Pour (x + 2) (x + 5), cela signifie que vous multipliez "2" et "x" pour obtenir "2x".
5 Multipliez les parties INNER dans chaque parenthèse. Les deux nombres les plus proches du centre seront votre terme interne. Pour (x + 2) (x + 5), cela signifie que vous multipliez "2" et "x" pour obtenir "2x". 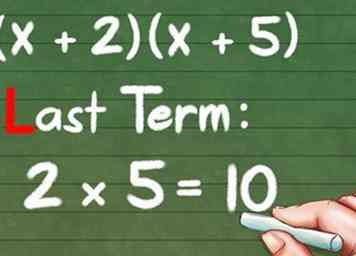 6 Multipliez les dernières parties de chaque parenthèse. Cela fait ne pas signifie les deux derniers chiffres, mais plutôt le dernier nombre entre parenthèses. Donc, pour (x + 2) (x + 5), nous multiplions le "2" et le "5" pour obtenir "10."
6 Multipliez les dernières parties de chaque parenthèse. Cela fait ne pas signifie les deux derniers chiffres, mais plutôt le dernier nombre entre parenthèses. Donc, pour (x + 2) (x + 5), nous multiplions le "2" et le "5" pour obtenir "10." 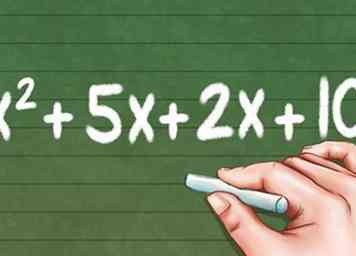 7 Ajoutez tous les nouveaux termes ensemble. Combinez les termes en les ajoutant ensemble pour créer une nouvelle expression plus grande. De notre exemple précédent, nous obtenons l'équation:
7 Ajoutez tous les nouveaux termes ensemble. Combinez les termes en les ajoutant ensemble pour créer une nouvelle expression plus grande. De notre exemple précédent, nous obtenons l'équation:  8 Simplifiez les termes similaires. Les termes similaires sont des parties de l'équation qui ont la même variable et le même pouvoir. Dans notre exemple, les termes 2x et 5x partagent tous deux un x et peuvent être ajoutés ensemble. Aucun autre terme ne se ressemble, alors ils restent.
8 Simplifiez les termes similaires. Les termes similaires sont des parties de l'équation qui ont la même variable et le même pouvoir. Dans notre exemple, les termes 2x et 5x partagent tous deux un x et peuvent être ajoutés ensemble. Aucun autre terme ne se ressemble, alors ils restent. 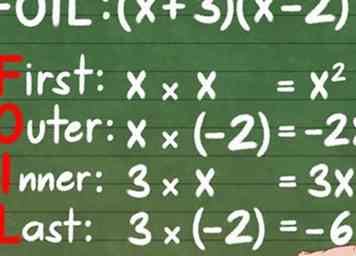 9 Rappelez-vous que les nombres soustraits sont négatifs. Lorsqu'un nombre est soustrait, cela revient à ajouter un nombre négatif. Si vous oubliez de garder le signe moins tout au long de vos calculs, vous vous retrouverez avec la mauvaise réponse. Prenons l'exemple (x + 3) (x-2):
9 Rappelez-vous que les nombres soustraits sont négatifs. Lorsqu'un nombre est soustrait, cela revient à ajouter un nombre négatif. Si vous oubliez de garder le signe moins tout au long de vos calculs, vous vous retrouverez avec la mauvaise réponse. Prenons l'exemple (x + 3) (x-2):  1 Multipliez les deux premiers binômes en ignorant temporairement le troisième. Prenons l'exemple (x + 4) (x + 1) (x + 3). Nous devons multiplier les binômes un par un, donc multipliez les deux par FOIL ou par distribution de termes. Multiplier les deux premiers (x + 4) et (x + 1) par FOIL ressemblerait à ceci:
1 Multipliez les deux premiers binômes en ignorant temporairement le troisième. Prenons l'exemple (x + 4) (x + 1) (x + 3). Nous devons multiplier les binômes un par un, donc multipliez les deux par FOIL ou par distribution de termes. Multiplier les deux premiers (x + 4) et (x + 1) par FOIL ressemblerait à ceci: 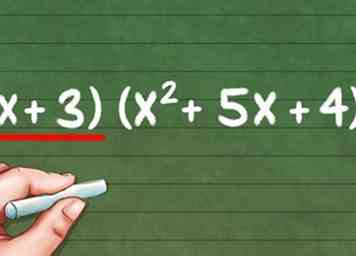 2 Combinez le binôme restant avec votre nouvelle équation. Maintenant que cette partie de l'équation a été multipliée, vous pouvez gérer le binôme restant. Dans l'exemple, (x + 4) (x + 1) (x + 3), le terme de surplus est (x + 3). Remettez-le avec la nouvelle équation, vous donnant: (x + 3) (x2 + 5x + 4).
2 Combinez le binôme restant avec votre nouvelle équation. Maintenant que cette partie de l'équation a été multipliée, vous pouvez gérer le binôme restant. Dans l'exemple, (x + 4) (x + 1) (x + 3), le terme de surplus est (x + 3). Remettez-le avec la nouvelle équation, vous donnant: (x + 3) (x2 + 5x + 4).  3 Multipliez le premier nombre du binôme par les trois nombres entre parenthèses. C'est la distribution des termes. Donc, pour l'équation (x + 3) (x2 + 5x + 4), vous devez multiplier le premier x par les trois parties de la deuxième parenthèse, "x2, "" 5x "et" 4. "
3 Multipliez le premier nombre du binôme par les trois nombres entre parenthèses. C'est la distribution des termes. Donc, pour l'équation (x + 3) (x2 + 5x + 4), vous devez multiplier le premier x par les trois parties de la deuxième parenthèse, "x2, "" 5x "et" 4. " 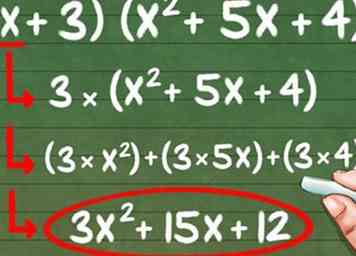 4 Multipliez le deuxième nombre dans le binôme par les trois nombres entre parenthèses. Prenez l'équation (x + 3) (x2 + 5x + 4). Maintenant, multipliez la deuxième partie du binôme par les trois parties entre parenthèses, "x2, "" 5x "et" 4. "
4 Multipliez le deuxième nombre dans le binôme par les trois nombres entre parenthèses. Prenez l'équation (x + 3) (x2 + 5x + 4). Maintenant, multipliez la deuxième partie du binôme par les trois parties entre parenthèses, "x2, "" 5x "et" 4. " 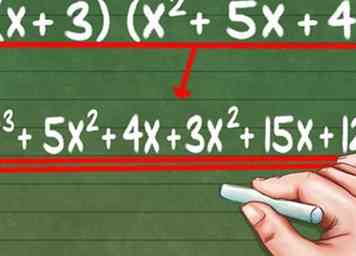 5 Additionnez les deux réponses de la multiplication. Vous devez combiner les réponses des deux étapes précédentes, car elles constituent les deux parties de votre réponse finale.
5 Additionnez les deux réponses de la multiplication. Vous devez combiner les réponses des deux étapes précédentes, car elles constituent les deux parties de votre réponse finale. 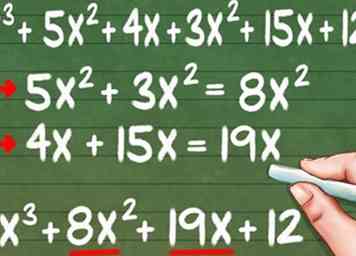 6 Simplifiez l'équation pour obtenir votre réponse finale. Tous les termes "similaires", termes qui partagent la même variable et la même puissance (comme 5x2 et 3x2), peuvent être ajoutés pour rendre votre réponse plus simple.
6 Simplifiez l'équation pour obtenir votre réponse finale. Tous les termes "similaires", termes qui partagent la même variable et la même puissance (comme 5x2 et 3x2), peuvent être ajoutés pour rendre votre réponse plus simple.  7 Toujours utiliser la distribution pour résoudre les problèmes de multiplication plus importants. Comme vous pouvez utiliser la distribution de termes pour multiplier des équations de n'importe quelle longueur, vous disposez désormais des outils nécessaires pour résoudre des problèmes plus importants, tels que (x + 1) (x + 2) (x + 3). Multipliez deux binômes en utilisant soit la distribution des termes ou FOIL, puis utilisez la distribution des termes pour multiplier le binôme final aux deux premiers. Dans l'exemple suivant, nous FOIL (x + 1) (x + 2), puis distribuons les termes avec (x + 3) pour obtenir la réponse finale:
7 Toujours utiliser la distribution pour résoudre les problèmes de multiplication plus importants. Comme vous pouvez utiliser la distribution de termes pour multiplier des équations de n'importe quelle longueur, vous disposez désormais des outils nécessaires pour résoudre des problèmes plus importants, tels que (x + 1) (x + 2) (x + 3). Multipliez deux binômes en utilisant soit la distribution des termes ou FOIL, puis utilisez la distribution des termes pour multiplier le binôme final aux deux premiers. Dans l'exemple suivant, nous FOIL (x + 1) (x + 2), puis distribuons les termes avec (x + 3) pour obtenir la réponse finale:  1 Savoir mettre en place "des formules générales."Les formules générales vous permettent de brancher simplement vos chiffres au lieu de calculer FOIL à chaque fois. Des binômes qui sont portés à la deuxième puissance, comme (x + 2)2, ou le troisième pouvoir, comme (4y + 12)3, peut être facilement adapté à une formule préexistante, ce qui rend la résolution rapide et facile. Pour trouver la formule générale, nous remplaçons tous les nombres par des variables. Ensuite, à la fin, nous pouvons relancer nos chiffres pour obtenir notre réponse. Commencez avec l'équation (a + b)2, où:
1 Savoir mettre en place "des formules générales."Les formules générales vous permettent de brancher simplement vos chiffres au lieu de calculer FOIL à chaque fois. Des binômes qui sont portés à la deuxième puissance, comme (x + 2)2, ou le troisième pouvoir, comme (4y + 12)3, peut être facilement adapté à une formule préexistante, ce qui rend la résolution rapide et facile. Pour trouver la formule générale, nous remplaçons tous les nombres par des variables. Ensuite, à la fin, nous pouvons relancer nos chiffres pour obtenir notre réponse. Commencez avec l'équation (a + b)2, où: 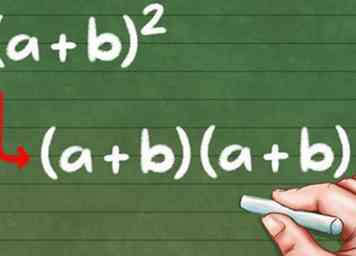 2 Sachez que les binômes carrés peuvent être réécrits. (a + b)2 peut sembler plus compliqué que notre exemple précédent, mais rappelez-vous que la quadrature d'un nombre ne fait que le multiplier par lui-même. Ainsi, nous pouvons réécrire l’équation pour la rendre plus familière:
2 Sachez que les binômes carrés peuvent être réécrits. (a + b)2 peut sembler plus compliqué que notre exemple précédent, mais rappelez-vous que la quadrature d'un nombre ne fait que le multiplier par lui-même. Ainsi, nous pouvons réécrire l’équation pour la rendre plus familière: 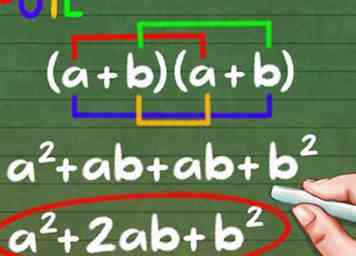 3 Utilisez FOIL pour résoudre la nouvelle équation. Si nous utilisons foil sur cette équation, nous aurons une formule générale qui ressemble à la solution à toute multiplication binomiale. Rappelez-vous que dans la multiplication, l'ordre que vous multipliez n'a pas d'importance
3 Utilisez FOIL pour résoudre la nouvelle équation. Si nous utilisons foil sur cette équation, nous aurons une formule générale qui ressemble à la solution à toute multiplication binomiale. Rappelez-vous que dans la multiplication, l'ordre que vous multipliez n'a pas d'importance 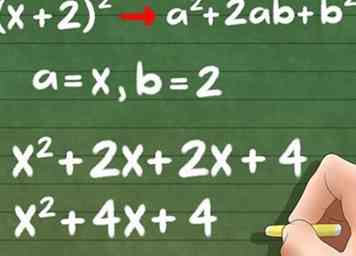 4 Utilisez l'équation générale a2 + 2ab + b2 pour résoudre vos problèmes. Prenons l'équation (x + 2)2. Au lieu de refaire le FOIL, nous pouvons insérer le premier terme pour "a" et le second terme pour "b",
4 Utilisez l'équation générale a2 + 2ab + b2 pour résoudre vos problèmes. Prenons l'équation (x + 2)2. Au lieu de refaire le FOIL, nous pouvons insérer le premier terme pour "a" et le second terme pour "b", 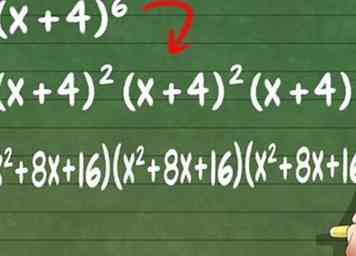 5 N'oubliez pas d'insérer le terme entier dans l'équation générale. Vu le binôme (2x + 3)2, vous devez vous rappeler que a = 2x, pas simplement a = 2. Lorsque vous avez des termes complexes, vous devez vous rappeler que les 2 et les x sont au carré.
5 N'oubliez pas d'insérer le terme entier dans l'équation générale. Vu le binôme (2x + 3)2, vous devez vous rappeler que a = 2x, pas simplement a = 2. Lorsque vous avez des termes complexes, vous devez vous rappeler que les 2 et les x sont au carré.