Une séquence arithmétique est une liste de nombres qui diffèrent d’une quantité à l’autre. Par exemple, la liste des nombres pairs, … Est une séquence arithmétique, car la différence entre un nombre dans la liste et la suivante est toujours 2. Si vous savez que vous travaillez avec une séquence arithmétique, vous pouvez être invité à trouver le terme suivant dans une liste donnée. Vous pouvez également être invité à combler une lacune où un terme est manquant. Enfin, vous voudrez peut-être savoir, par exemple, le 100ème terme, sans pour autant écrire les 100 termes. Quelques étapes simples peuvent vous aider à faire l'une de ces actions.
Méthode One of Four:
Recherche du terme suivant dans une séquence arithmétique
-
 1 Trouvez la différence commune pour la séquence. Lorsqu'on vous présente une liste de numéros, on peut vous dire que la liste est une séquence arithmétique ou que vous devez vous en rendre compte. La première étape est la même dans les deux cas. Sélectionnez les deux premiers termes consécutifs dans la liste. Soustrayez le premier terme du deuxième terme. Le résultat est la différence commune de votre séquence.[1]
1 Trouvez la différence commune pour la séquence. Lorsqu'on vous présente une liste de numéros, on peut vous dire que la liste est une séquence arithmétique ou que vous devez vous en rendre compte. La première étape est la même dans les deux cas. Sélectionnez les deux premiers termes consécutifs dans la liste. Soustrayez le premier terme du deuxième terme. Le résultat est la différence commune de votre séquence.[1] - Par exemple, supposons que vous ayez la liste … Soustraire pour trouver la différence commune de 3.
- Supposons que vous ayez une liste de termes qui diminue, tels que …. Vous soustrayez toujours le premier terme de la seconde pour trouver la différence. Dans ce cas, cela vous donne . Le résultat négatif signifie que votre liste diminue à mesure que vous lisez de gauche à droite. Vous devriez toujours vérifier que le signe de la différence correspond à la direction dans laquelle les chiffres semblent aller.
-
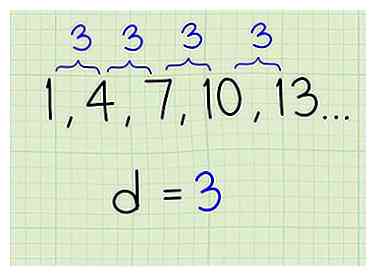 2 Vérifiez que la différence commune est cohérente. Trouver la différence commune pour les deux premiers termes ne garantit pas que votre liste est une séquence arithmétique. Vous devez vous assurer que la différence est cohérente pour toute la liste. Vérifiez la différence en soustrayant deux termes consécutifs différents dans la liste. Si le résultat est cohérent pour une ou deux autres paires de termes, alors vous avez probablement une séquence arithmétique.
2 Vérifiez que la différence commune est cohérente. Trouver la différence commune pour les deux premiers termes ne garantit pas que votre liste est une séquence arithmétique. Vous devez vous assurer que la différence est cohérente pour toute la liste. Vérifiez la différence en soustrayant deux termes consécutifs différents dans la liste. Si le résultat est cohérent pour une ou deux autres paires de termes, alors vous avez probablement une séquence arithmétique. - Travailler avec le même exemple, … Choisissez les deuxième et troisième termes de la liste. Soustraire et vous constatez que la différence est toujours 3. Pour confirmer, cochez un autre exemple et soustrayez , et vous trouvez que la différence est toujours 3. Vous pouvez être sûr que vous travaillez avec une séquence arithmétique.
- Il est possible qu'une liste de nombres apparaisse comme une séquence arithmétique basée sur les premiers termes, mais échoue ensuite. Par exemple, considérons la liste …. La différence entre les premier et deuxième termes est 1, et la différence entre les deuxième et troisième termes est également 1. Cependant, la différence entre les troisième et quatrième termes est 3. Comme la différence n'est pas commune à la liste entière, alors cette différence n'est pas une séquence arithmétique.
-
 3 Ajouter la différence commune au dernier terme donné. Il est facile de trouver le terme suivant d'une séquence arithmétique après avoir compris la différence commune. Ajoutez simplement la différence commune au dernier terme de la liste et vous obtiendrez le numéro suivant.
3 Ajouter la différence commune au dernier terme donné. Il est facile de trouver le terme suivant d'une séquence arithmétique après avoir compris la différence commune. Ajoutez simplement la différence commune au dernier terme de la liste et vous obtiendrez le numéro suivant. - Par exemple, dans l'exemple de …, Pour trouver le numéro suivant dans la liste, ajoutez la différence commune de 3 au dernier terme donné. Ajouter donne 16, qui est le prochain terme. Vous pouvez continuer à ajouter 3 pour faire votre liste aussi longtemps que vous le souhaitez. Par exemple, la liste serait …. Vous pouvez le faire aussi longtemps que vous le souhaitez.
Méthode deux sur quatre:
Trouver un terme interne manquant
-
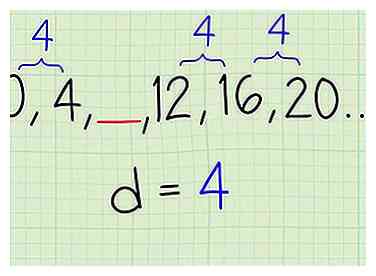 1 Vérifiez que vous commencez par une séquence arithmétique. Dans certains cas, vous pouvez avoir une liste de numéros avec un terme manquant au milieu. Commencez comme précédemment en vérifiant que votre liste est une séquence arithmétique. Sélectionnez deux termes consécutifs et trouvez la différence entre eux. Ensuite, vérifiez cela contre deux autres termes consécutifs dans la liste. Si les différences sont les mêmes, vous pouvez supposer que vous travaillez avec une séquence arithmétique et continuer.
1 Vérifiez que vous commencez par une séquence arithmétique. Dans certains cas, vous pouvez avoir une liste de numéros avec un terme manquant au milieu. Commencez comme précédemment en vérifiant que votre liste est une séquence arithmétique. Sélectionnez deux termes consécutifs et trouvez la différence entre eux. Ensuite, vérifiez cela contre deux autres termes consécutifs dans la liste. Si les différences sont les mêmes, vous pouvez supposer que vous travaillez avec une séquence arithmétique et continuer. - Par exemple, supposons que vous ayez la liste ,___,…. Commencez par soustraire pour trouver une différence de 4. Cochez ceci contre deux autres termes consécutifs, tels que . La différence est de nouveau 4. Vous pouvez continuer.
-
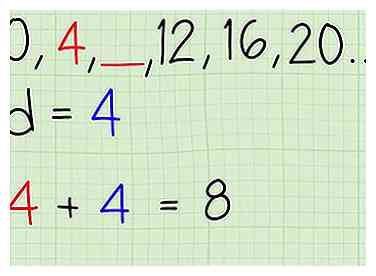 2 Ajoutez la différence commune au terme avant l'espace. Cela revient à ajouter un terme à la fin d'une séquence. Trouvez le terme qui précède immédiatement l'espace dans votre séquence. C'est le dernier numéro que vous connaissez. Ajoutez votre différence commune à ce terme, pour trouver le nombre qui devrait remplir l'espace.
2 Ajoutez la différence commune au terme avant l'espace. Cela revient à ajouter un terme à la fin d'une séquence. Trouvez le terme qui précède immédiatement l'espace dans votre séquence. C'est le dernier numéro que vous connaissez. Ajoutez votre différence commune à ce terme, pour trouver le nombre qui devrait remplir l'espace. - Dans notre exemple de travail, ,____,…, Le terme qui précède l’espace est 4, et notre différence commune pour cette liste est aussi 4. Alors ajoutez pour obtenir 8, qui devrait être le nombre dans l'espace vide.
-
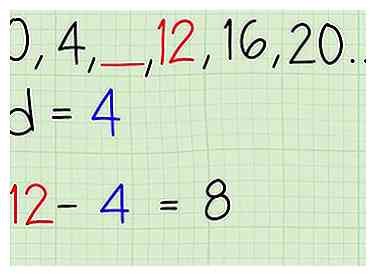 3 Soustrayez la différence commune du terme qui suit l'espace. Pour être sûr d'avoir la bonne réponse, vérifiez dans l'autre sens. Une séquence arithmétique devrait être cohérente dans les deux sens.Si vous vous déplacez de gauche à droite et ajoutez 4, puis allez dans la direction opposée, de droite à gauche, vous feriez le contraire et soustrayez 4.
3 Soustrayez la différence commune du terme qui suit l'espace. Pour être sûr d'avoir la bonne réponse, vérifiez dans l'autre sens. Une séquence arithmétique devrait être cohérente dans les deux sens.Si vous vous déplacez de gauche à droite et ajoutez 4, puis allez dans la direction opposée, de droite à gauche, vous feriez le contraire et soustrayez 4. - Dans l'exemple de travail, ,___,…, Le terme qui suit immédiatement l’espace est 12. Soustrayez la différence commune de 4 de ce terme pour trouver . Le résultat de 8 devrait remplir l'espace vide.
-
 4 Comparez vos résultats. Les deux résultats que vous obtenez, en additionnant depuis le bas ou en les soustrayant, doivent correspondre. Si c'est le cas, vous avez trouvé la valeur du terme manquant. Si ce n'est pas le cas, vous devez vérifier votre travail. Vous ne pouvez pas avoir une véritable séquence arithmétique.
4 Comparez vos résultats. Les deux résultats que vous obtenez, en additionnant depuis le bas ou en les soustrayant, doivent correspondre. Si c'est le cas, vous avez trouvé la valeur du terme manquant. Si ce n'est pas le cas, vous devez vérifier votre travail. Vous ne pouvez pas avoir une véritable séquence arithmétique. - Dans l'exemple de travail, les deux résultats de et les deux ont donné la solution de 8. Par conséquent, le terme manquant dans cette séquence arithmétique est 8. La séquence complète est … .
Méthode trois sur quatre:
Trouver le nième terme d'une séquence arithmétique
-
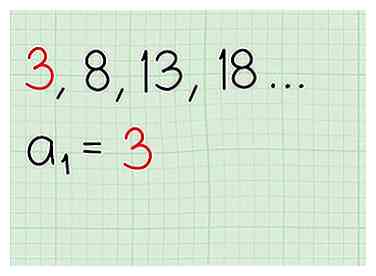 1 Identifier le premier terme de la séquence. Toutes les séquences ne commencent pas par les chiffres 0 ou 1. Regardez la liste des nombres que vous avez et trouvez le premier terme. Ceci est votre point de départ, qui peut être désigné en utilisant des variables en tant que (1).
1 Identifier le premier terme de la séquence. Toutes les séquences ne commencent pas par les chiffres 0 ou 1. Regardez la liste des nombres que vous avez et trouvez le premier terme. Ceci est votre point de départ, qui peut être désigné en utilisant des variables en tant que (1). - En travaillant avec des séquences arithmétiques, il est courant d'utiliser la variable a (1) pour désigner le premier terme d'une séquence. Vous pouvez bien sûr choisir une variable qui vous plait et les résultats doivent être les mêmes.
- Par exemple, compte tenu de la séquence …, Le premier terme est , qui peut être désigné algébriquement en tant que (1).
-
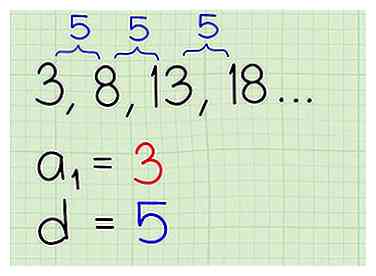 2 Définissez votre différence commune comme d. Trouvez la différence commune pour la séquence comme avant. Dans cet exemple de travail, la différence commune est , qui est 5. Vérifier avec d'autres termes dans la séquence fournit le même résultat. Nous noterons cette différence commune avec la variable algébrique d.
2 Définissez votre différence commune comme d. Trouvez la différence commune pour la séquence comme avant. Dans cet exemple de travail, la différence commune est , qui est 5. Vérifier avec d'autres termes dans la séquence fournit le même résultat. Nous noterons cette différence commune avec la variable algébrique d. -
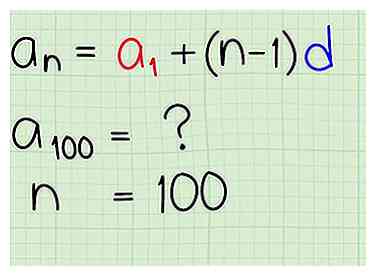 3 Utilisez la formule explicite. Une formule explicite est une équation algébrique que vous pouvez utiliser pour trouver n'importe quel terme d'une séquence arithmétique sans avoir à écrire la liste complète. La formule explicite d'une séquence algébrique est .
3 Utilisez la formule explicite. Une formule explicite est une équation algébrique que vous pouvez utiliser pour trouver n'importe quel terme d'une séquence arithmétique sans avoir à écrire la liste complète. La formule explicite d'une séquence algébrique est . - Le terme a (n) peut être lu comme «le nième terme de a», où n représente le nombre dans la liste que vous voulez trouver et a (n) la valeur réelle de ce nombre. Par exemple, si on vous demande de trouver le 100ème élément dans une séquence arithmétique, alors n sera 100. Notez que n est 100, dans cet exemple, mais qu'un (n) sera la valeur du 100ème terme, pas le nombre 100 lui-même.
-
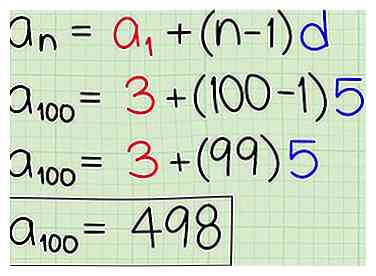 4 Remplissez vos informations pour résoudre le problème. En utilisant la formule explicite de votre séquence, remplissez les informations que vous connaissez pour trouver le terme dont vous avez besoin.
4 Remplissez vos informations pour résoudre le problème. En utilisant la formule explicite de votre séquence, remplissez les informations que vous connaissez pour trouver le terme dont vous avez besoin. - Par exemple, dans l'exemple de travail …, Nous savons qu'un (1) est le premier terme 3 et la différence commune d est 5. Supposons qu'on vous demande de trouver le 100ème terme dans cette séquence. Alors n = 100 et (n-1) = 99. La formule explicite complète, avec les données renseignées, est alors . Cela simplifie à 498, qui est le 100ème terme de cette séquence.
Méthode quatre sur quatre:
Utilisation de la formule explicite pour trouver des informations supplémentaires
-
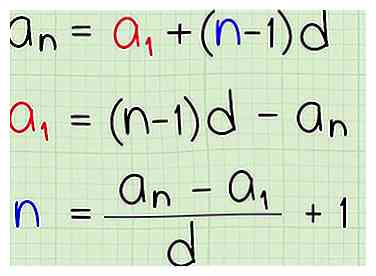 1 Réorganiser la formule explicite pour résoudre d'autres variables. En utilisant la formule explicite et une algèbre de base, vous pouvez trouver plusieurs informations sur une séquence arithmétique. Dans sa forme originale, , la formule explicite est conçue pour résoudre pour unn et vous donner le nième terme d'une séquence. Cependant, vous pouvez manipuler algébriquement cette formule et résoudre toutes les variables.
1 Réorganiser la formule explicite pour résoudre d'autres variables. En utilisant la formule explicite et une algèbre de base, vous pouvez trouver plusieurs informations sur une séquence arithmétique. Dans sa forme originale, , la formule explicite est conçue pour résoudre pour unn et vous donner le nième terme d'une séquence. Cependant, vous pouvez manipuler algébriquement cette formule et résoudre toutes les variables. - Par exemple, supposons que vous ayez la fin d'une liste de nombres, mais vous devez connaître le début de la séquence. Vous pouvez réorganiser la formule pour vous donner
- Si vous connaissez le point de départ d'une séquence arithmétique et son point de fin, mais que vous devez connaître le nombre de termes dans la liste, vous pouvez réorganiser la formule explicite pour résoudre n. Ce serait .
- Si vous avez besoin de revoir les règles de base de l'algèbre pour créer ce résultat, consultez Do Algebra ou Simplify Algebraic Expressions.
-
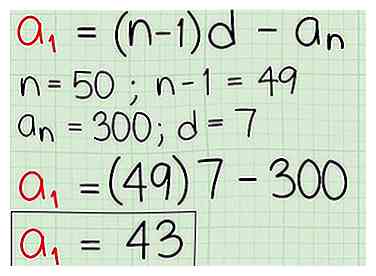 2 Trouvez le premier terme d'une séquence. Vous savez peut-être que le 50ème terme d'une séquence arithmétique est 300, et vous savez que les termes ont augmenté de 7 (la «différence commune»), mais vous voulez savoir quel était le premier terme de la séquence. Utilisez la formule explicite révisée qui permet à a1 de trouver votre réponse.
2 Trouvez le premier terme d'une séquence. Vous savez peut-être que le 50ème terme d'une séquence arithmétique est 300, et vous savez que les termes ont augmenté de 7 (la «différence commune»), mais vous voulez savoir quel était le premier terme de la séquence. Utilisez la formule explicite révisée qui permet à a1 de trouver votre réponse. - Utiliser l'équation et remplissez les informations que vous connaissez. Puisque vous savez que le 50ème terme est 300, alors n = 50, n-1 = 49 et a (n) = 300. On vous dit également que la différence commune, d, est 7. Par conséquent, la formule devient . Cela fonctionne à . La séquence que vous avez commencée à 43 et comptée par 7. Par conséquent, cela ressemble à 43,50,57,64,71,78… 293,300.
-
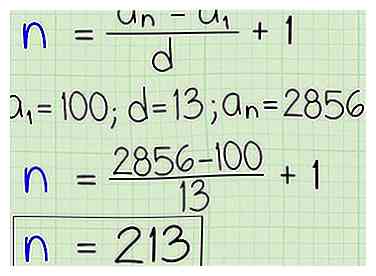 3 Trouvez la longueur d'une séquence. Supposons que vous sachiez tout sur le début et la fin d'une séquence arithmétique, mais vous devez savoir combien de temps cela dure. Utiliser la formule révisée .
3 Trouvez la longueur d'une séquence. Supposons que vous sachiez tout sur le début et la fin d'une séquence arithmétique, mais vous devez savoir combien de temps cela dure. Utiliser la formule révisée . - Supposons que vous sachiez qu'une séquence arithmétique donnée commence à 100 et augmente de 13. On vous dit également que le dernier terme est de 2 856. Pour trouver la longueur de la séquence, utilisez les termes a1 = 100, d = 13 et a (n) = 2856. Insérer ces termes dans la formule pour donner . Si vous travaillez cela, vous obtenez , qui est égal à 212 + 1, qui est 213. Il y a 213 termes dans cette séquence.
- Cette séquence d'échantillonnage ressemblerait à 100, 113, 126, 139… 2843, 2856.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Trouvez la différence commune pour la séquence. Lorsqu'on vous présente une liste de numéros, on peut vous dire que la liste est une séquence arithmétique ou que vous devez vous en rendre compte. La première étape est la même dans les deux cas. Sélectionnez les deux premiers termes consécutifs dans la liste. Soustrayez le premier terme du deuxième terme. Le résultat est la différence commune de votre séquence.[1]
1 Trouvez la différence commune pour la séquence. Lorsqu'on vous présente une liste de numéros, on peut vous dire que la liste est une séquence arithmétique ou que vous devez vous en rendre compte. La première étape est la même dans les deux cas. Sélectionnez les deux premiers termes consécutifs dans la liste. Soustrayez le premier terme du deuxième terme. Le résultat est la différence commune de votre séquence.[1] 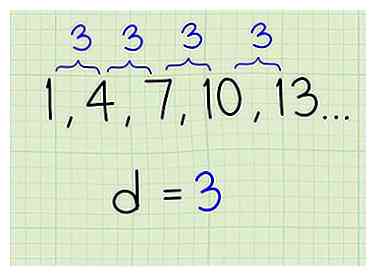 2 Vérifiez que la différence commune est cohérente. Trouver la différence commune pour les deux premiers termes ne garantit pas que votre liste est une séquence arithmétique. Vous devez vous assurer que la différence est cohérente pour toute la liste. Vérifiez la différence en soustrayant deux termes consécutifs différents dans la liste. Si le résultat est cohérent pour une ou deux autres paires de termes, alors vous avez probablement une séquence arithmétique.
2 Vérifiez que la différence commune est cohérente. Trouver la différence commune pour les deux premiers termes ne garantit pas que votre liste est une séquence arithmétique. Vous devez vous assurer que la différence est cohérente pour toute la liste. Vérifiez la différence en soustrayant deux termes consécutifs différents dans la liste. Si le résultat est cohérent pour une ou deux autres paires de termes, alors vous avez probablement une séquence arithmétique.  3 Ajouter la différence commune au dernier terme donné. Il est facile de trouver le terme suivant d'une séquence arithmétique après avoir compris la différence commune. Ajoutez simplement la différence commune au dernier terme de la liste et vous obtiendrez le numéro suivant.
3 Ajouter la différence commune au dernier terme donné. Il est facile de trouver le terme suivant d'une séquence arithmétique après avoir compris la différence commune. Ajoutez simplement la différence commune au dernier terme de la liste et vous obtiendrez le numéro suivant. 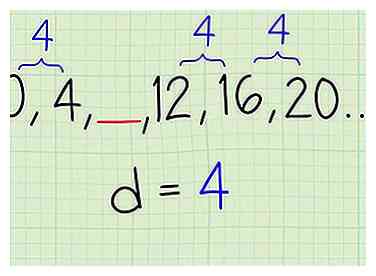 1 Vérifiez que vous commencez par une séquence arithmétique. Dans certains cas, vous pouvez avoir une liste de numéros avec un terme manquant au milieu. Commencez comme précédemment en vérifiant que votre liste est une séquence arithmétique. Sélectionnez deux termes consécutifs et trouvez la différence entre eux. Ensuite, vérifiez cela contre deux autres termes consécutifs dans la liste. Si les différences sont les mêmes, vous pouvez supposer que vous travaillez avec une séquence arithmétique et continuer.
1 Vérifiez que vous commencez par une séquence arithmétique. Dans certains cas, vous pouvez avoir une liste de numéros avec un terme manquant au milieu. Commencez comme précédemment en vérifiant que votre liste est une séquence arithmétique. Sélectionnez deux termes consécutifs et trouvez la différence entre eux. Ensuite, vérifiez cela contre deux autres termes consécutifs dans la liste. Si les différences sont les mêmes, vous pouvez supposer que vous travaillez avec une séquence arithmétique et continuer. 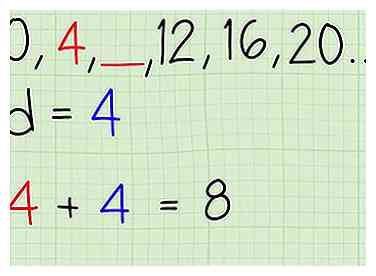 2 Ajoutez la différence commune au terme avant l'espace. Cela revient à ajouter un terme à la fin d'une séquence. Trouvez le terme qui précède immédiatement l'espace dans votre séquence. C'est le dernier numéro que vous connaissez. Ajoutez votre différence commune à ce terme, pour trouver le nombre qui devrait remplir l'espace.
2 Ajoutez la différence commune au terme avant l'espace. Cela revient à ajouter un terme à la fin d'une séquence. Trouvez le terme qui précède immédiatement l'espace dans votre séquence. C'est le dernier numéro que vous connaissez. Ajoutez votre différence commune à ce terme, pour trouver le nombre qui devrait remplir l'espace. 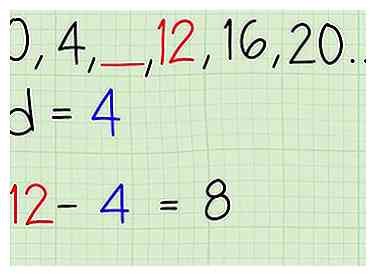 3 Soustrayez la différence commune du terme qui suit l'espace. Pour être sûr d'avoir la bonne réponse, vérifiez dans l'autre sens. Une séquence arithmétique devrait être cohérente dans les deux sens.Si vous vous déplacez de gauche à droite et ajoutez 4, puis allez dans la direction opposée, de droite à gauche, vous feriez le contraire et soustrayez 4.
3 Soustrayez la différence commune du terme qui suit l'espace. Pour être sûr d'avoir la bonne réponse, vérifiez dans l'autre sens. Une séquence arithmétique devrait être cohérente dans les deux sens.Si vous vous déplacez de gauche à droite et ajoutez 4, puis allez dans la direction opposée, de droite à gauche, vous feriez le contraire et soustrayez 4.  4 Comparez vos résultats. Les deux résultats que vous obtenez, en additionnant depuis le bas ou en les soustrayant, doivent correspondre. Si c'est le cas, vous avez trouvé la valeur du terme manquant. Si ce n'est pas le cas, vous devez vérifier votre travail. Vous ne pouvez pas avoir une véritable séquence arithmétique.
4 Comparez vos résultats. Les deux résultats que vous obtenez, en additionnant depuis le bas ou en les soustrayant, doivent correspondre. Si c'est le cas, vous avez trouvé la valeur du terme manquant. Si ce n'est pas le cas, vous devez vérifier votre travail. Vous ne pouvez pas avoir une véritable séquence arithmétique. 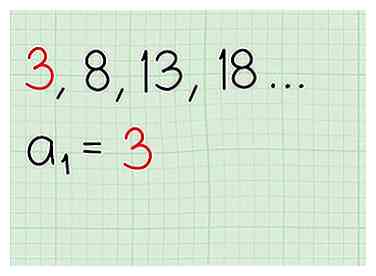 1 Identifier le premier terme de la séquence. Toutes les séquences ne commencent pas par les chiffres 0 ou 1. Regardez la liste des nombres que vous avez et trouvez le premier terme. Ceci est votre point de départ, qui peut être désigné en utilisant des variables en tant que (1).
1 Identifier le premier terme de la séquence. Toutes les séquences ne commencent pas par les chiffres 0 ou 1. Regardez la liste des nombres que vous avez et trouvez le premier terme. Ceci est votre point de départ, qui peut être désigné en utilisant des variables en tant que (1). 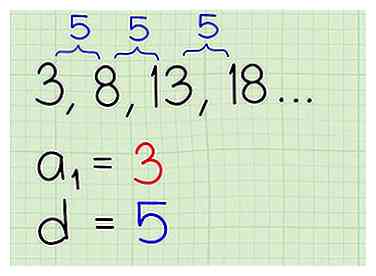 2 Définissez votre différence commune comme d. Trouvez la différence commune pour la séquence comme avant. Dans cet exemple de travail, la différence commune est
2 Définissez votre différence commune comme d. Trouvez la différence commune pour la séquence comme avant. Dans cet exemple de travail, la différence commune est 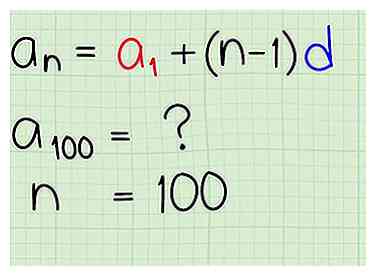 3 Utilisez la formule explicite. Une formule explicite est une équation algébrique que vous pouvez utiliser pour trouver n'importe quel terme d'une séquence arithmétique sans avoir à écrire la liste complète. La formule explicite d'une séquence algébrique est
3 Utilisez la formule explicite. Une formule explicite est une équation algébrique que vous pouvez utiliser pour trouver n'importe quel terme d'une séquence arithmétique sans avoir à écrire la liste complète. La formule explicite d'une séquence algébrique est 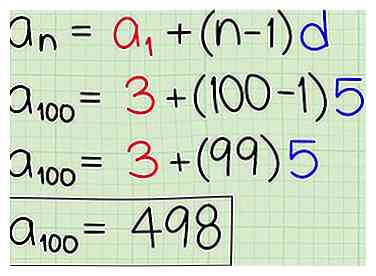 4 Remplissez vos informations pour résoudre le problème. En utilisant la formule explicite de votre séquence, remplissez les informations que vous connaissez pour trouver le terme dont vous avez besoin.
4 Remplissez vos informations pour résoudre le problème. En utilisant la formule explicite de votre séquence, remplissez les informations que vous connaissez pour trouver le terme dont vous avez besoin. 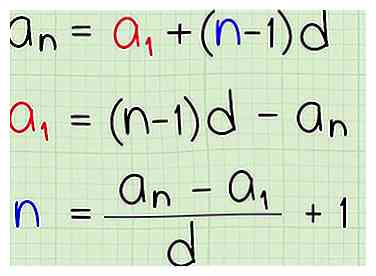 1 Réorganiser la formule explicite pour résoudre d'autres variables. En utilisant la formule explicite et une algèbre de base, vous pouvez trouver plusieurs informations sur une séquence arithmétique. Dans sa forme originale,
1 Réorganiser la formule explicite pour résoudre d'autres variables. En utilisant la formule explicite et une algèbre de base, vous pouvez trouver plusieurs informations sur une séquence arithmétique. Dans sa forme originale, 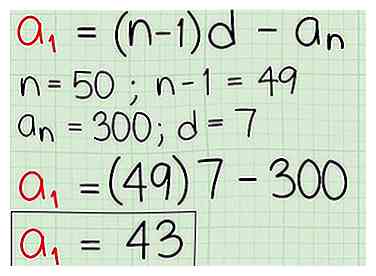 2 Trouvez le premier terme d'une séquence. Vous savez peut-être que le 50ème terme d'une séquence arithmétique est 300, et vous savez que les termes ont augmenté de 7 (la «différence commune»), mais vous voulez savoir quel était le premier terme de la séquence. Utilisez la formule explicite révisée qui permet à a1 de trouver votre réponse.
2 Trouvez le premier terme d'une séquence. Vous savez peut-être que le 50ème terme d'une séquence arithmétique est 300, et vous savez que les termes ont augmenté de 7 (la «différence commune»), mais vous voulez savoir quel était le premier terme de la séquence. Utilisez la formule explicite révisée qui permet à a1 de trouver votre réponse. 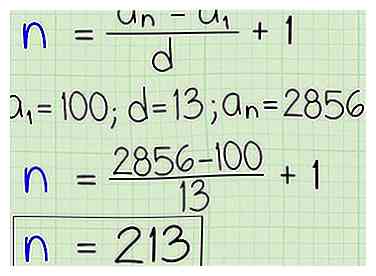 3 Trouvez la longueur d'une séquence. Supposons que vous sachiez tout sur le début et la fin d'une séquence arithmétique, mais vous devez savoir combien de temps cela dure. Utiliser la formule révisée
3 Trouvez la longueur d'une séquence. Supposons que vous sachiez tout sur le début et la fin d'une séquence arithmétique, mais vous devez savoir combien de temps cela dure. Utiliser la formule révisée