Ceci est un article sur la façon de factoriser un 3rd polynôme de degré. Nous explorerons comment factoriser en utilisant le regroupement ainsi que l'utilisation des facteurs du terme libre.
Première partie de deux:
Affacturage en groupant
-
 1 Groupez le polynôme en deux sections. En regroupant le polynôme en deux sections, vous pourrez attaquer chaque section individuellement.
1 Groupez le polynôme en deux sections. En regroupant le polynôme en deux sections, vous pourrez attaquer chaque section individuellement. - Disons que nous travaillons avec le polynôme x3 + 3x2 - 6x - 18 = 0. Regroupons-le dans (x3 + 3x2) et (- 6x - 18)
-
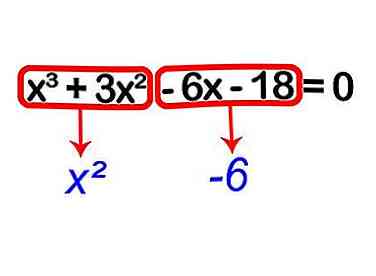 2 Trouvez ce qui est commun dans chaque section.
2 Trouvez ce qui est commun dans chaque section. - En regardant (x3 + 3x2), on peut voir que x2 est commun.
- En regardant (- 6x - 18), nous pouvons voir que -6 est commun.
-
 3 Facteur les points communs des deux termes.
3 Facteur les points communs des deux termes. - Affacturage x2 de la première section, nous obtenons x2(x + 3).
- En tenant compte de -6 de la deuxième section, vous obtiendrez -6 (x + 3).
-
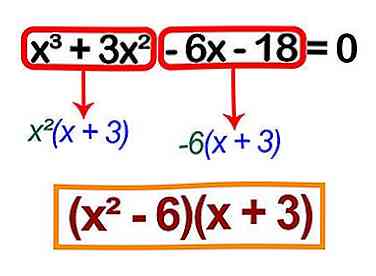 4 Si chacun des deux termes contient le même facteur, vous pouvez combiner les facteurs ensemble.
4 Si chacun des deux termes contient le même facteur, vous pouvez combiner les facteurs ensemble. - Cela vous donne (x + 3) (x2 - 6).
-
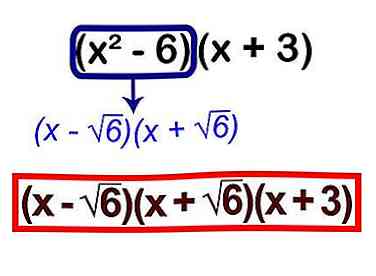 5 Trouvez la solution en regardant les racines. Si vous avez un x2 dans vos racines, rappelez-vous que tous les deux les nombres négatifs et positifs remplissent cette équation.
5 Trouvez la solution en regardant les racines. Si vous avez un x2 dans vos racines, rappelez-vous que tous les deux les nombres négatifs et positifs remplissent cette équation. - Les solutions sont -3, √6 et -√6.
Deuxième partie de deux:
Factoring en utilisant le terme libre
-
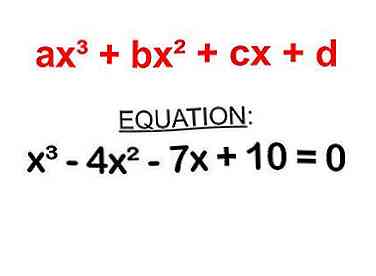 1 Réorganiser l'expression pour qu'elle soit sous la forme de aX3+ bX2+ cX + d.
1 Réorganiser l'expression pour qu'elle soit sous la forme de aX3+ bX2+ cX + d. - Disons que vous travaillez avec l'équation: x3 - 4x2 - 7x + 10 = 0
-
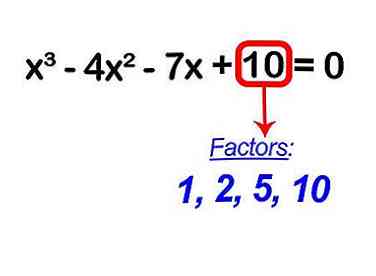 2 Trouve tous les facteurs de "d". La constante "d" sera le nombre qui n'a pas de variables, telles que "x", à côté de lui.
2 Trouve tous les facteurs de "d". La constante "d" sera le nombre qui n'a pas de variables, telles que "x", à côté de lui. - Les facteurs sont les nombres que vous pouvez multiplier ensemble pour obtenir un autre numéro. Dans votre cas, les facteurs 10 ou d sont: 1, 2, 5 et 10.
-
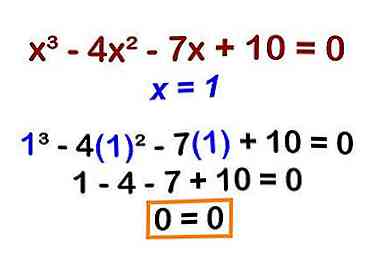 3 Trouvez un facteur qui fait que le polynôme est égal à zéro. Nous voulons déterminer quel facteur rend le polynôme égal à zéro lorsque nous substituons le facteur pour chaque "x" de l'équation.
3 Trouvez un facteur qui fait que le polynôme est égal à zéro. Nous voulons déterminer quel facteur rend le polynôme égal à zéro lorsque nous substituons le facteur pour chaque "x" de l'équation. - Commencez par utiliser votre premier facteur, 1. Remplacez "1" pour chaque "x" de l'équation:
(1)3 - 4(1)2 - 7(1) + 10 = 0 - Cela vous donne: 1 - 4 - 7 + 10 = 0.
- Parce que 0 = 0 est une déclaration vraie, vous savez que x = 1 est une solution.
- Commencez par utiliser votre premier facteur, 1. Remplacez "1" pour chaque "x" de l'équation:
-
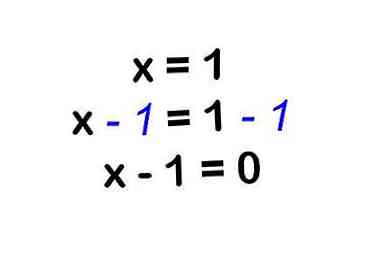 4 Faites un peu de réarrangement. Si x = 1, vous pouvez réorganiser l'instruction pour qu'elle soit un peu différente sans changer ce que cela signifie.
4 Faites un peu de réarrangement. Si x = 1, vous pouvez réorganiser l'instruction pour qu'elle soit un peu différente sans changer ce que cela signifie. - "x = 1" est la même chose que "x - 1 = 0" ou "(x - 1)". Vous venez de soustraire un "1" de chaque côté de l'équation.
-
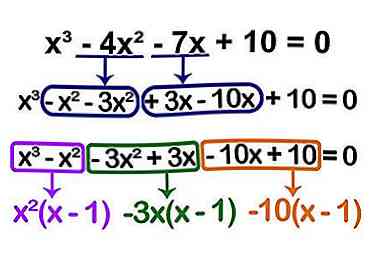 5 Facteur votre racine du reste de l'équation. "(x - 1)" est notre racine. Voyez si vous pouvez le factoriser du reste de l'équation. Prenez-le un polynôme à la fois.
5 Facteur votre racine du reste de l'équation. "(x - 1)" est notre racine. Voyez si vous pouvez le factoriser du reste de l'équation. Prenez-le un polynôme à la fois. - Pouvez-vous factoriser (x - 1) sur les x3? Non tu ne peux pas. Mais vous pouvez emprunter un -x2 à partir de la deuxième variable; alors le facteur: x2(x - 1) = x3 - X2.
- Pouvez-vous prendre en compte (x - 1) ce qui reste de votre deuxième variable? Non, encore une fois, tu ne peux pas. Vous devez emprunter un autre petit bout de la troisième variable. Vous devez emprunter un 3x de -7x. Cela vous donne -3x (x - 1) = -3x2 + 3x.
- Comme vous avez pris un 3x de -7x, notre troisième variable est maintenant -10x et notre constante est 10. Pouvez-vous prendre cela en compte? Vous pouvez! -10 (x - 1) = -10x + 10.
- Ce que vous avez fait a été de réorganiser les variables pour pouvoir éliminer un (x - 1) de l'équation entière. Votre équation réarrangée ressemble à ceci: x3 - X2 - 3x2 + 3x - 10x + 10 = 0, mais c'est toujours la même chose que x3 - 4x2 - 7x + 10 = 0.
-
 6 Continuer à substituer par les facteurs du terme libre. Regardez les chiffres que vous avez pris en compte en utilisant le (x - 1) à l’étape 5:
6 Continuer à substituer par les facteurs du terme libre. Regardez les chiffres que vous avez pris en compte en utilisant le (x - 1) à l’étape 5: - X2(x - 1) - 3x (x - 1) - 10 (x - 1) = 0. Vous pouvez réorganiser ceci pour être plus facile à factoriser une fois de plus: (x - 1) (x2 - 3x - 10) = 0.
- Vous essayez seulement de prendre en compte (x2 - 3x - 10) ici. Cela revient à (x + 2) (x - 5).
-
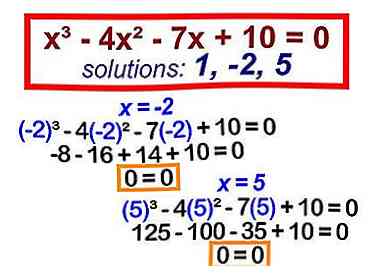 7 Vos solutions seront les racines pondérées. Vous pouvez vérifier si vos solutions fonctionnent réellement en branchant chacune d'elles, individuellement, dans l'équation d'origine.
7 Vos solutions seront les racines pondérées. Vous pouvez vérifier si vos solutions fonctionnent réellement en branchant chacune d'elles, individuellement, dans l'équation d'origine. - (x - 1) (x + 2) (x - 5) = 0 Cela vous donne des solutions de 1, -2 et 5.
- Branchez -2 dans l'équation: (-2)3 - 4(-2)2 - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0.
- Branchez 5 dans l'équation: (5)3 - 4(5)2 - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Groupez le polynôme en deux sections. En regroupant le polynôme en deux sections, vous pourrez attaquer chaque section individuellement.
1 Groupez le polynôme en deux sections. En regroupant le polynôme en deux sections, vous pourrez attaquer chaque section individuellement. 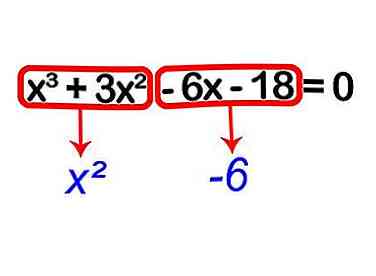 2 Trouvez ce qui est commun dans chaque section.
2 Trouvez ce qui est commun dans chaque section.  3 Facteur les points communs des deux termes.
3 Facteur les points communs des deux termes. 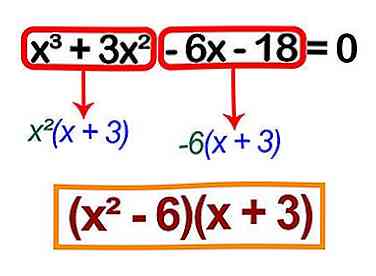 4 Si chacun des deux termes contient le même facteur, vous pouvez combiner les facteurs ensemble.
4 Si chacun des deux termes contient le même facteur, vous pouvez combiner les facteurs ensemble. 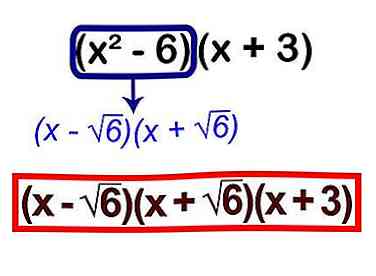 5 Trouvez la solution en regardant les racines. Si vous avez un x2 dans vos racines, rappelez-vous que tous les deux les nombres négatifs et positifs remplissent cette équation.
5 Trouvez la solution en regardant les racines. Si vous avez un x2 dans vos racines, rappelez-vous que tous les deux les nombres négatifs et positifs remplissent cette équation. 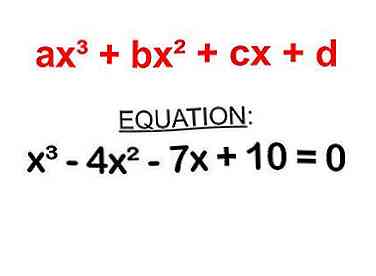 1 Réorganiser l'expression pour qu'elle soit sous la forme de aX3+ bX2+ cX + d.
1 Réorganiser l'expression pour qu'elle soit sous la forme de aX3+ bX2+ cX + d. 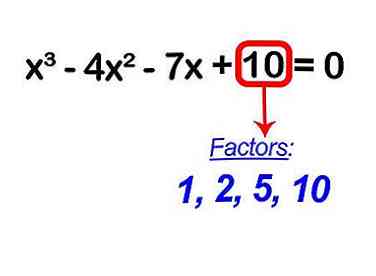 2 Trouve tous les facteurs de "d". La constante "d" sera le nombre qui n'a pas de variables, telles que "x", à côté de lui.
2 Trouve tous les facteurs de "d". La constante "d" sera le nombre qui n'a pas de variables, telles que "x", à côté de lui. 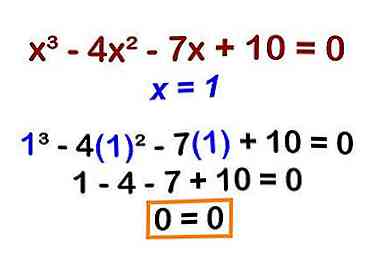 3 Trouvez un facteur qui fait que le polynôme est égal à zéro. Nous voulons déterminer quel facteur rend le polynôme égal à zéro lorsque nous substituons le facteur pour chaque "x" de l'équation.
3 Trouvez un facteur qui fait que le polynôme est égal à zéro. Nous voulons déterminer quel facteur rend le polynôme égal à zéro lorsque nous substituons le facteur pour chaque "x" de l'équation. 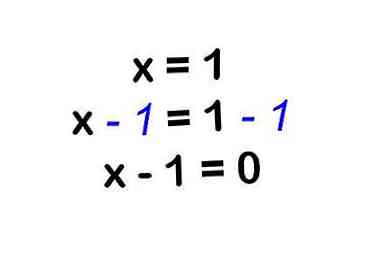 4 Faites un peu de réarrangement. Si x = 1, vous pouvez réorganiser l'instruction pour qu'elle soit un peu différente sans changer ce que cela signifie.
4 Faites un peu de réarrangement. Si x = 1, vous pouvez réorganiser l'instruction pour qu'elle soit un peu différente sans changer ce que cela signifie. 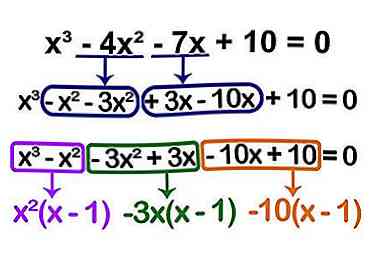 5 Facteur votre racine du reste de l'équation. "(x - 1)" est notre racine. Voyez si vous pouvez le factoriser du reste de l'équation. Prenez-le un polynôme à la fois.
5 Facteur votre racine du reste de l'équation. "(x - 1)" est notre racine. Voyez si vous pouvez le factoriser du reste de l'équation. Prenez-le un polynôme à la fois.  6 Continuer à substituer par les facteurs du terme libre. Regardez les chiffres que vous avez pris en compte en utilisant le (x - 1) à l’étape 5:
6 Continuer à substituer par les facteurs du terme libre. Regardez les chiffres que vous avez pris en compte en utilisant le (x - 1) à l’étape 5: 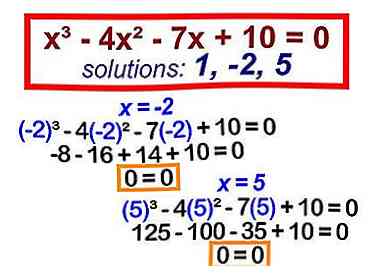 7 Vos solutions seront les racines pondérées. Vous pouvez vérifier si vos solutions fonctionnent réellement en branchant chacune d'elles, individuellement, dans l'équation d'origine.
7 Vos solutions seront les racines pondérées. Vous pouvez vérifier si vos solutions fonctionnent réellement en branchant chacune d'elles, individuellement, dans l'équation d'origine.