En algèbre, les binômes sont des expressions à deux termes reliées par un signe plus ou un signe moins, comme . Le premier terme inclut toujours une variable, tandis que le second terme peut ou non. Affecter un binôme signifie trouver des termes plus simples qui, multipliés ensemble, produisent cette expression binomiale, ce qui vous aide à le résoudre ou à le simplifier pour un travail ultérieur.
Première partie de trois:
Binomials d'affacturage
-
 1 Passez en revue les bases de l'affacturage. L'affacturage est lorsque vous divisez un grand nombre en parties divisibles les plus simples. Chacune de ces parties est appelée "facteur". Ainsi, par exemple, le nombre 6 peut être divisé par quatre nombres différents: 1, 2, 3 et 6. Ainsi, les facteurs 6 sont 1, 2, 3 et 6.
1 Passez en revue les bases de l'affacturage. L'affacturage est lorsque vous divisez un grand nombre en parties divisibles les plus simples. Chacune de ces parties est appelée "facteur". Ainsi, par exemple, le nombre 6 peut être divisé par quatre nombres différents: 1, 2, 3 et 6. Ainsi, les facteurs 6 sont 1, 2, 3 et 6. - Les facteurs de 32 sont 1, 2, 4, 8, 16 et 32
- "1" et le nombre que vous factorisez sont toujours des facteurs. Ainsi, les facteurs d'un petit nombre, comme 3, seraient simplement 1 et 3.
- Les facteurs ne sont que les nombres parfaitement divisibles ou les nombres "entiers". Vous pourriez diviser 32 par 3.564, ou 21.4952, mais cela ne conduira pas à un facteur, juste une autre décimale.
-
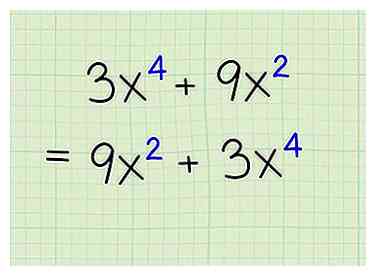 2 Placez les termes du binôme afin de les rendre plus lisibles. Un binôme est simplement l'addition ou la soustraction de deux nombres, dont l'un au moins contient une variable. Parfois, ces variables ont des exposants, comme ou . Lors de la première factorisation de binômes, cela peut aider à réorganiser les équations avec des termes variables ascendants, ce qui signifie que le plus grand exposant est le dernier. Par exemple:
2 Placez les termes du binôme afin de les rendre plus lisibles. Un binôme est simplement l'addition ou la soustraction de deux nombres, dont l'un au moins contient une variable. Parfois, ces variables ont des exposants, comme ou . Lors de la première factorisation de binômes, cela peut aider à réorganiser les équations avec des termes variables ascendants, ce qui signifie que le plus grand exposant est le dernier. Par exemple: - →
- →
- →
- Notez comment le signe négatif reste devant le 2. Si un terme est soustrait, gardez juste le négatif devant lui.
-
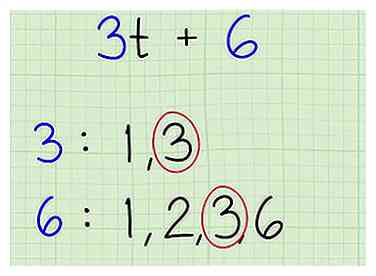 3 Trouvez le plus grand facteur commun aux deux termes. Cela signifie que vous trouvez le plus grand nombre possible que les deux parties du binôme soient divisibles par. Si vous éprouvez des difficultés, intégrez simplement les deux chiffres, puis voyez quel est le nombre le plus élevé correspondant. Par exemple:
3 Trouvez le plus grand facteur commun aux deux termes. Cela signifie que vous trouvez le plus grand nombre possible que les deux parties du binôme soient divisibles par. Si vous éprouvez des difficultés, intégrez simplement les deux chiffres, puis voyez quel est le nombre le plus élevé correspondant. Par exemple: - Problème de pratique:.
- Facteurs de 3: 1, 3
- Facteurs de 6: 1, 2, 3, 6.
- Le plus grand facteur commun est 3.
- Problème de pratique:.
-
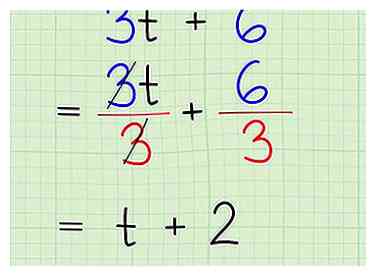 4 Diviser le plus grand facteur commun de chaque terme. Une fois que vous connaissez votre facteur commun, vous devez le supprimer de chaque terme. Notez, cependant, que vous ne faites que briser les termes, transformant chaque terme en un petit problème de division. Si vous l'avez bien fait, les deux équations partageront votre facteur:
4 Diviser le plus grand facteur commun de chaque terme. Une fois que vous connaissez votre facteur commun, vous devez le supprimer de chaque terme. Notez, cependant, que vous ne faites que briser les termes, transformant chaque terme en un petit problème de division. Si vous l'avez bien fait, les deux équations partageront votre facteur: - Problème de pratique:.
- Trouver le plus grand facteur commun: 3
- Supprimer le facteur des deux termes:
-
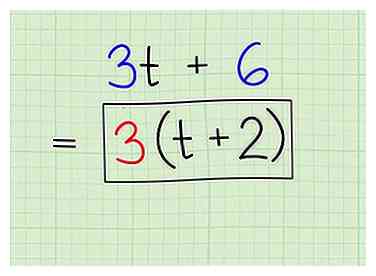 5 Multipliez votre facteur par l'expression résultante pour terminer. Dans le dernier problème, vous avez retiré un 3 pour obtenir . Mais vous ne vous débarrassiez pas uniquement des trois, simplement en les simplifiant. Vous ne pouvez pas simplement effacer les chiffres sans les remettre! Multipliez votre facteur par l'expression pour finir enfin. Par exemple:
5 Multipliez votre facteur par l'expression résultante pour terminer. Dans le dernier problème, vous avez retiré un 3 pour obtenir . Mais vous ne vous débarrassiez pas uniquement des trois, simplement en les simplifiant. Vous ne pouvez pas simplement effacer les chiffres sans les remettre! Multipliez votre facteur par l'expression pour finir enfin. Par exemple: - Problème de pratique:
- Trouver le plus grand facteur commun: 3
- Supprimer le facteur des deux termes:
- Facteur multiple par nouvelle expression:
- Réponse factorielle finale:
-
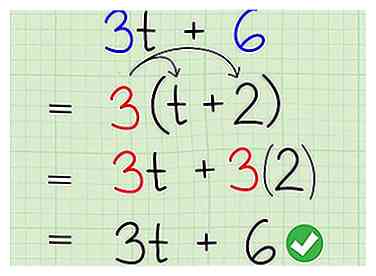 6 Vérifiez votre travail en le multipliant par l’équation originale. Si vous avez tout fait correctement, vérifier que vous avez bien compris devrait être facile. Multipliez simplement votre facteur par les deux parties individuelles de la parenthèse. Si elle correspond au binôme original, non construit, vous avez tout fait correctement. Du début à la fin, résolvez l'expression s'entraîner:
6 Vérifiez votre travail en le multipliant par l’équation originale. Si vous avez tout fait correctement, vérifier que vous avez bien compris devrait être facile. Multipliez simplement votre facteur par les deux parties individuelles de la parenthèse. Si elle correspond au binôme original, non construit, vous avez tout fait correctement. Du début à la fin, résolvez l'expression s'entraîner: - Réorganiser les termes:
- Trouver le plus grand dénominateur commun:
- Supprimer le facteur des deux termes:
- Facteur multiple par nouvelle expression:
- Vérifier la réponse:
Deuxième partie de trois:
Affacturage des binômes pour résoudre des équations
-
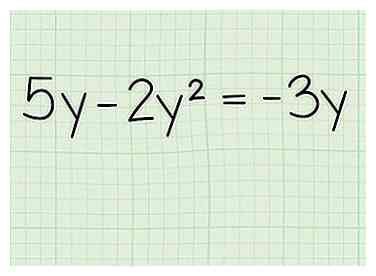 1 Utilisez le factoring pour simplifier les équations et les rendre plus faciles à résoudre. Lors de la résolution d'une équation avec des binômes, en particulier des binômes complexes, il peut sembler impossible de tout faire correspondre. Par exemple, essayez de résoudre . Une façon de le résoudre, en particulier avec les exposants, est de prendre en compte en premier.
1 Utilisez le factoring pour simplifier les équations et les rendre plus faciles à résoudre. Lors de la résolution d'une équation avec des binômes, en particulier des binômes complexes, il peut sembler impossible de tout faire correspondre. Par exemple, essayez de résoudre . Une façon de le résoudre, en particulier avec les exposants, est de prendre en compte en premier. - Problème de pratique:
- Rappelez-vous que les binômes ne doivent avoir que deux termes. S'il y a plus de deux termes, vous pouvez apprendre à résoudre des polynômes à la place.
-
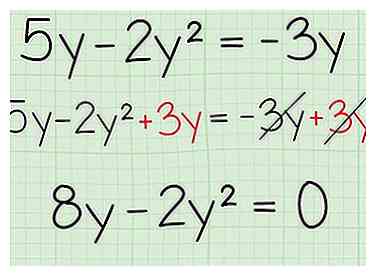 2 Ajoutez et soustrayez pour qu'un côté de l'équation soit égal à zéro. Toute cette stratégie repose sur l'un des faits les plus fondamentaux des mathématiques: tout ce qui est multiplié par zéro doit être égal à zéro. Donc, si votre équation est égale à zéro, alors l'un de vos termes pondérés doit être égal à zéro! Pour commencer, ajouter et soustraire un côté est égal à zéro.
2 Ajoutez et soustrayez pour qu'un côté de l'équation soit égal à zéro. Toute cette stratégie repose sur l'un des faits les plus fondamentaux des mathématiques: tout ce qui est multiplié par zéro doit être égal à zéro. Donc, si votre équation est égale à zéro, alors l'un de vos termes pondérés doit être égal à zéro! Pour commencer, ajouter et soustraire un côté est égal à zéro. - Problème de pratique:
- Mettre à zéro:
-
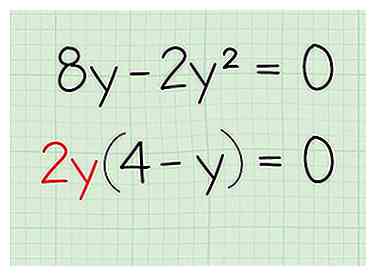 3 Factorise le côté non nul comme si c'était normal. À ce stade, vous pouvez prétendre que l'autre côté n'existe pas pour une étape. Trouvez simplement le meilleur facteur commun, divisez-le et créez votre expression factorisée.
3 Factorise le côté non nul comme si c'était normal. À ce stade, vous pouvez prétendre que l'autre côté n'existe pas pour une étape. Trouvez simplement le meilleur facteur commun, divisez-le et créez votre expression factorisée. - Problème de pratique:
- Mettre à zéro:
- Facteur:
-
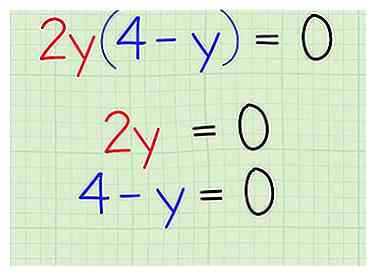 4 Définissez les deux à l'intérieur et à l'extérieur de la parenthèse comme étant égal à zéro. Dans le problème de pratique, vous multipliez 2 ans par 4 ans, et il doit être égal à zéro. Comme tout ce qui est multiplié par zéro est égal à zéro, cela signifie que 2y ou 4 - y doit être 0. Créez deux équations distinctes pour déterminer ce que doit être pour chaque côté égal à zéro.
4 Définissez les deux à l'intérieur et à l'extérieur de la parenthèse comme étant égal à zéro. Dans le problème de pratique, vous multipliez 2 ans par 4 ans, et il doit être égal à zéro. Comme tout ce qui est multiplié par zéro est égal à zéro, cela signifie que 2y ou 4 - y doit être 0. Créez deux équations distinctes pour déterminer ce que doit être pour chaque côté égal à zéro. - Problème de pratique:
- Mettre à zéro:
- Facteur:
- Définissez les deux parties sur 0:
-
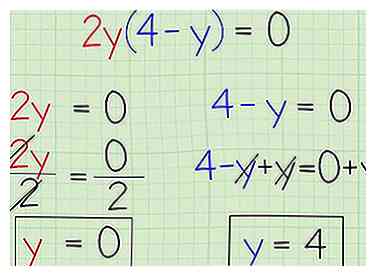 5 Résolvez les deux équations à zéro pour obtenir votre ou vos réponses finales. Vous pourriez avoir une réponse, ou plus d'une. N'oubliez pas qu'un seul côté doit être égal à zéro, vous pouvez donc obtenir quelques valeurs différentes de y qui résolvent la même équation. Pour le problème de la fin de la pratique:
5 Résolvez les deux équations à zéro pour obtenir votre ou vos réponses finales. Vous pourriez avoir une réponse, ou plus d'une. N'oubliez pas qu'un seul côté doit être égal à zéro, vous pouvez donc obtenir quelques valeurs différentes de y qui résolvent la même équation. Pour le problème de la fin de la pratique: -
- y = 0
-
- y = 4
-
-
 6 Rebranchez vos réponses pour vous assurer qu'elles fonctionnent. Si vous avez les bonnes valeurs pour y, vous devriez pouvoir les utiliser pour résoudre l'équation. Il est simple d’essayer chaque valeur de y à la place de la variable, comme indiqué. Puisque la réponse était y = 0 et y = 4:
6 Rebranchez vos réponses pour vous assurer qu'elles fonctionnent. Si vous avez les bonnes valeurs pour y, vous devriez pouvoir les utiliser pour résoudre l'équation. Il est simple d’essayer chaque valeur de y à la place de la variable, comme indiqué. Puisque la réponse était y = 0 et y = 4: -
- Cette réponse est correcte
-
- Cette réponse est également correcte.
-
Troisième partie de trois:
Gestion des problèmes plus complexes
-
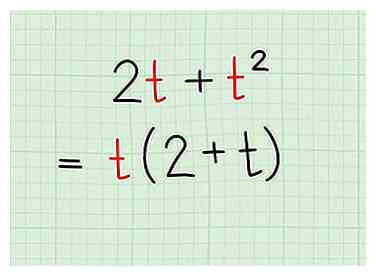 1 Rappelez-vous que les variables comptent également comme facteurs, même avec les exposants. Rappelez-vous que l'affacturage consiste à déterminer quels nombres peuvent être répartis dans l'ensemble. L'expression est une autre façon de dire . Cela signifie que vous pouvez factoriser chaque x si l'autre terme en a un aussi. Traiter les variables non différentes d'un nombre normal. Par exemple:
1 Rappelez-vous que les variables comptent également comme facteurs, même avec les exposants. Rappelez-vous que l'affacturage consiste à déterminer quels nombres peuvent être répartis dans l'ensemble. L'expression est une autre façon de dire . Cela signifie que vous pouvez factoriser chaque x si l'autre terme en a un aussi. Traiter les variables non différentes d'un nombre normal. Par exemple: - peut être prise en compte, car les deux termes contiennent un t. Votre réponse finale serait
- Vous pouvez même extraire plusieurs variables à la fois. Par exemple, dans les deux termes contiennent les mêmes . Vous pouvez prendre en compte
-
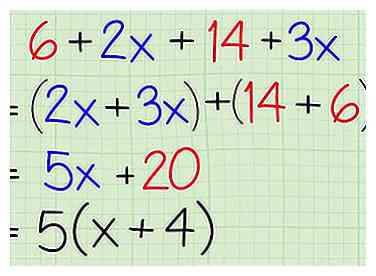 2 Reconnaître les binômes non simplifiés en combinant des termes similaires. Prenez, par exemple, l'expression . Cela peut sembler avoir quatre termes, mais regardez bien et vous réaliserez qu'il n'y en a que deux. Vous pouvez ajouter des termes similaires, et puisque les 6 et 14 n'ont pas de variable, et que les 2x et 3x partagent la même variable, ils peuvent tous deux être combinés. L’affacturage est alors facile:
2 Reconnaître les binômes non simplifiés en combinant des termes similaires. Prenez, par exemple, l'expression . Cela peut sembler avoir quatre termes, mais regardez bien et vous réaliserez qu'il n'y en a que deux. Vous pouvez ajouter des termes similaires, et puisque les 6 et 14 n'ont pas de variable, et que les 2x et 3x partagent la même variable, ils peuvent tous deux être combinés. L’affacturage est alors facile: - Problème d'origine:
- Réorganiser les termes:
- Combinez comme termes:
- Trouver le plus grand facteur commun:
- Facteur:
-
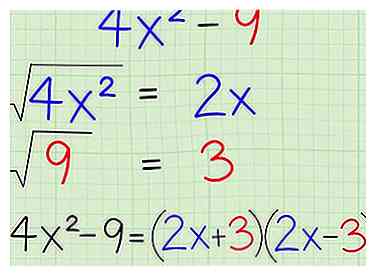 3 Reconnaître la différence particulière des carrés parfaits."Un carré parfait est un nombre dont la racine carrée est un nombre entier, comme , , ou même Si votre binôme est un problème de soustraction avec deux carrés parfaits, comme , vous pouvez simplement les brancher dans cette formule:
3 Reconnaître la différence particulière des carrés parfaits."Un carré parfait est un nombre dont la racine carrée est un nombre entier, comme , , ou même Si votre binôme est un problème de soustraction avec deux carrés parfaits, comme , vous pouvez simplement les brancher dans cette formule: - Différence de formule des carrés parfaits:
- Problème de pratique:
- Trouvez des racines carrées:
- Branchez les carrés dans la formule: [1]
-
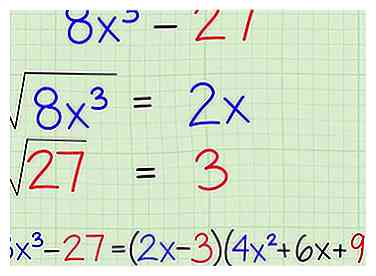 4 Apprenez à décomposer la "différence de cubes parfaits"."Tout comme les carrés parfaits, il s’agit d’une formule simple pour laquelle deux termes cubes sont soustraits. Par exemple, . Tout comme avant, vous trouvez simplement la racine cubique de chacun, en les branchant dans une formule:
4 Apprenez à décomposer la "différence de cubes parfaits"."Tout comme les carrés parfaits, il s’agit d’une formule simple pour laquelle deux termes cubes sont soustraits. Par exemple, . Tout comme avant, vous trouvez simplement la racine cubique de chacun, en les branchant dans une formule: - Différence de formule de cubes parfaits:
- Problème de pratique:
- Trouver des racines en cubes:
- Branchez les cubes dans la formule: [2]
-
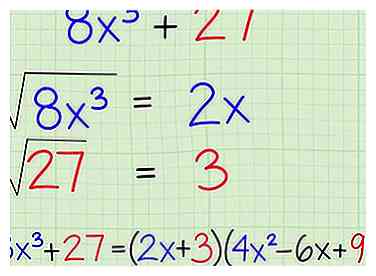 5 Sachez que la somme des cubes parfaits tient aussi dans une formule. Contrairement à la différence des carrés parfaits, vous pouvez facilement trouver des cubes ajoutés, comme , avec une formule simple C'est presque le même que ci-dessus, avec quelques avantages et inconvénients. La formule est aussi simple que les deux autres et il suffit de reconnaître les deux cubes du problème pour l’utiliser:
5 Sachez que la somme des cubes parfaits tient aussi dans une formule. Contrairement à la différence des carrés parfaits, vous pouvez facilement trouver des cubes ajoutés, comme , avec une formule simple C'est presque le même que ci-dessus, avec quelques avantages et inconvénients. La formule est aussi simple que les deux autres et il suffit de reconnaître les deux cubes du problème pour l’utiliser: - Somme de la formule parfaite des cubes:
- Problème de pratique:
- Trouver des racines en cubes:
- Branchez les cubes dans la formule: [3]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Passez en revue les bases de l'affacturage. L'affacturage est lorsque vous divisez un grand nombre en parties divisibles les plus simples. Chacune de ces parties est appelée "facteur". Ainsi, par exemple, le nombre 6 peut être divisé par quatre nombres différents: 1, 2, 3 et 6. Ainsi, les facteurs 6 sont 1, 2, 3 et 6.
1 Passez en revue les bases de l'affacturage. L'affacturage est lorsque vous divisez un grand nombre en parties divisibles les plus simples. Chacune de ces parties est appelée "facteur". Ainsi, par exemple, le nombre 6 peut être divisé par quatre nombres différents: 1, 2, 3 et 6. Ainsi, les facteurs 6 sont 1, 2, 3 et 6. 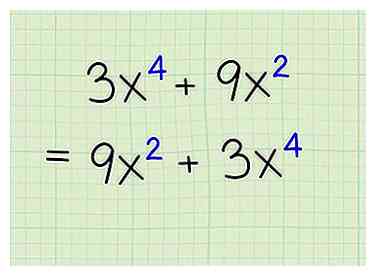 2 Placez les termes du binôme afin de les rendre plus lisibles. Un binôme est simplement l'addition ou la soustraction de deux nombres, dont l'un au moins contient une variable. Parfois, ces variables ont des exposants, comme
2 Placez les termes du binôme afin de les rendre plus lisibles. Un binôme est simplement l'addition ou la soustraction de deux nombres, dont l'un au moins contient une variable. Parfois, ces variables ont des exposants, comme 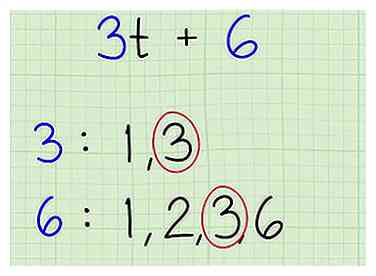 3 Trouvez le plus grand facteur commun aux deux termes. Cela signifie que vous trouvez le plus grand nombre possible que les deux parties du binôme soient divisibles par. Si vous éprouvez des difficultés, intégrez simplement les deux chiffres, puis voyez quel est le nombre le plus élevé correspondant. Par exemple:
3 Trouvez le plus grand facteur commun aux deux termes. Cela signifie que vous trouvez le plus grand nombre possible que les deux parties du binôme soient divisibles par. Si vous éprouvez des difficultés, intégrez simplement les deux chiffres, puis voyez quel est le nombre le plus élevé correspondant. Par exemple: 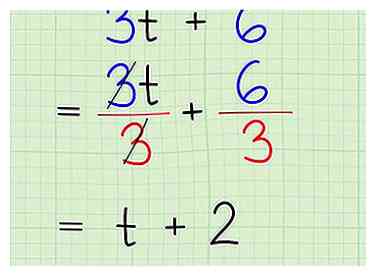 4 Diviser le plus grand facteur commun de chaque terme. Une fois que vous connaissez votre facteur commun, vous devez le supprimer de chaque terme. Notez, cependant, que vous ne faites que briser les termes, transformant chaque terme en un petit problème de division. Si vous l'avez bien fait, les deux équations partageront votre facteur:
4 Diviser le plus grand facteur commun de chaque terme. Une fois que vous connaissez votre facteur commun, vous devez le supprimer de chaque terme. Notez, cependant, que vous ne faites que briser les termes, transformant chaque terme en un petit problème de division. Si vous l'avez bien fait, les deux équations partageront votre facteur: 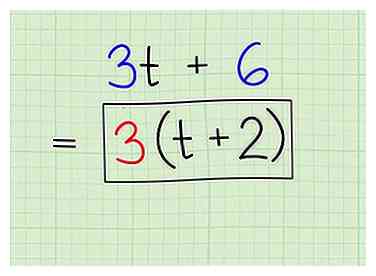 5 Multipliez votre facteur par l'expression résultante pour terminer. Dans le dernier problème, vous avez retiré un 3 pour obtenir
5 Multipliez votre facteur par l'expression résultante pour terminer. Dans le dernier problème, vous avez retiré un 3 pour obtenir 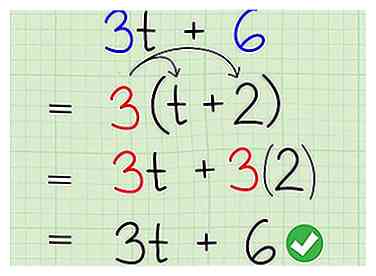 6 Vérifiez votre travail en le multipliant par l’équation originale. Si vous avez tout fait correctement, vérifier que vous avez bien compris devrait être facile. Multipliez simplement votre facteur par les deux parties individuelles de la parenthèse. Si elle correspond au binôme original, non construit, vous avez tout fait correctement. Du début à la fin, résolvez l'expression
6 Vérifiez votre travail en le multipliant par l’équation originale. Si vous avez tout fait correctement, vérifier que vous avez bien compris devrait être facile. Multipliez simplement votre facteur par les deux parties individuelles de la parenthèse. Si elle correspond au binôme original, non construit, vous avez tout fait correctement. Du début à la fin, résolvez l'expression 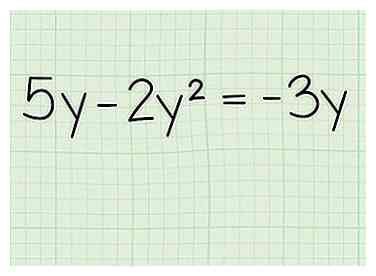 1 Utilisez le factoring pour simplifier les équations et les rendre plus faciles à résoudre. Lors de la résolution d'une équation avec des binômes, en particulier des binômes complexes, il peut sembler impossible de tout faire correspondre. Par exemple, essayez de résoudre
1 Utilisez le factoring pour simplifier les équations et les rendre plus faciles à résoudre. Lors de la résolution d'une équation avec des binômes, en particulier des binômes complexes, il peut sembler impossible de tout faire correspondre. Par exemple, essayez de résoudre 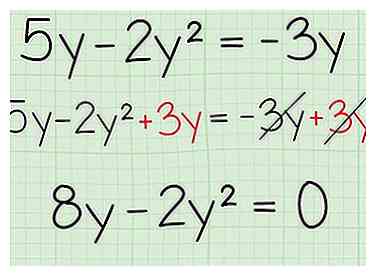 2 Ajoutez et soustrayez pour qu'un côté de l'équation soit égal à zéro. Toute cette stratégie repose sur l'un des faits les plus fondamentaux des mathématiques: tout ce qui est multiplié par zéro doit être égal à zéro. Donc, si votre équation est égale à zéro, alors l'un de vos termes pondérés doit être égal à zéro! Pour commencer, ajouter et soustraire un côté est égal à zéro.
2 Ajoutez et soustrayez pour qu'un côté de l'équation soit égal à zéro. Toute cette stratégie repose sur l'un des faits les plus fondamentaux des mathématiques: tout ce qui est multiplié par zéro doit être égal à zéro. Donc, si votre équation est égale à zéro, alors l'un de vos termes pondérés doit être égal à zéro! Pour commencer, ajouter et soustraire un côté est égal à zéro. 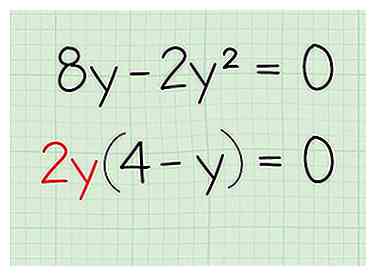 3 Factorise le côté non nul comme si c'était normal. À ce stade, vous pouvez prétendre que l'autre côté n'existe pas pour une étape. Trouvez simplement le meilleur facteur commun, divisez-le et créez votre expression factorisée.
3 Factorise le côté non nul comme si c'était normal. À ce stade, vous pouvez prétendre que l'autre côté n'existe pas pour une étape. Trouvez simplement le meilleur facteur commun, divisez-le et créez votre expression factorisée. 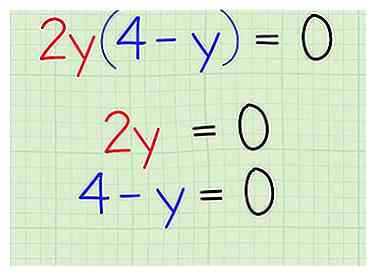 4 Définissez les deux à l'intérieur et à l'extérieur de la parenthèse comme étant égal à zéro. Dans le problème de pratique, vous multipliez 2 ans par 4 ans, et il doit être égal à zéro. Comme tout ce qui est multiplié par zéro est égal à zéro, cela signifie que 2y ou 4 - y doit être 0. Créez deux équations distinctes pour déterminer ce que doit être pour chaque côté égal à zéro.
4 Définissez les deux à l'intérieur et à l'extérieur de la parenthèse comme étant égal à zéro. Dans le problème de pratique, vous multipliez 2 ans par 4 ans, et il doit être égal à zéro. Comme tout ce qui est multiplié par zéro est égal à zéro, cela signifie que 2y ou 4 - y doit être 0. Créez deux équations distinctes pour déterminer ce que doit être pour chaque côté égal à zéro. 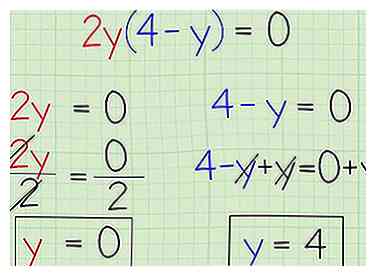 5 Résolvez les deux équations à zéro pour obtenir votre ou vos réponses finales. Vous pourriez avoir une réponse, ou plus d'une. N'oubliez pas qu'un seul côté doit être égal à zéro, vous pouvez donc obtenir quelques valeurs différentes de y qui résolvent la même équation. Pour le problème de la fin de la pratique:
5 Résolvez les deux équations à zéro pour obtenir votre ou vos réponses finales. Vous pourriez avoir une réponse, ou plus d'une. N'oubliez pas qu'un seul côté doit être égal à zéro, vous pouvez donc obtenir quelques valeurs différentes de y qui résolvent la même équation. Pour le problème de la fin de la pratique:  6 Rebranchez vos réponses pour vous assurer qu'elles fonctionnent. Si vous avez les bonnes valeurs pour y, vous devriez pouvoir les utiliser pour résoudre l'équation. Il est simple d’essayer chaque valeur de y à la place de la variable, comme indiqué. Puisque la réponse était y = 0 et y = 4:
6 Rebranchez vos réponses pour vous assurer qu'elles fonctionnent. Si vous avez les bonnes valeurs pour y, vous devriez pouvoir les utiliser pour résoudre l'équation. Il est simple d’essayer chaque valeur de y à la place de la variable, comme indiqué. Puisque la réponse était y = 0 et y = 4: 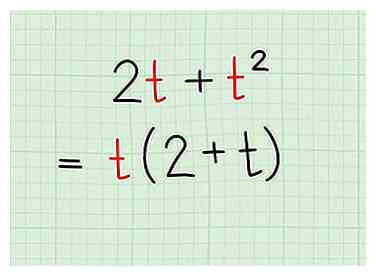 1 Rappelez-vous que les variables comptent également comme facteurs, même avec les exposants. Rappelez-vous que l'affacturage consiste à déterminer quels nombres peuvent être répartis dans l'ensemble. L'expression
1 Rappelez-vous que les variables comptent également comme facteurs, même avec les exposants. Rappelez-vous que l'affacturage consiste à déterminer quels nombres peuvent être répartis dans l'ensemble. L'expression 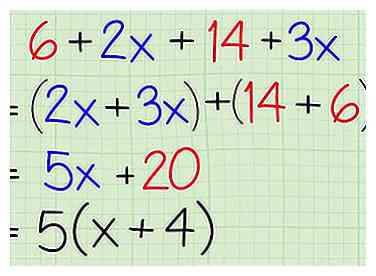 2 Reconnaître les binômes non simplifiés en combinant des termes similaires. Prenez, par exemple, l'expression
2 Reconnaître les binômes non simplifiés en combinant des termes similaires. Prenez, par exemple, l'expression 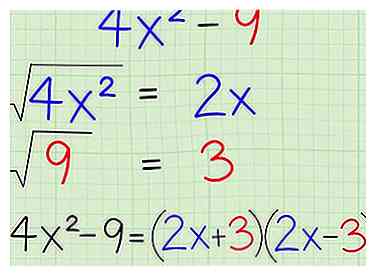 3 Reconnaître la différence particulière des carrés parfaits."Un carré parfait est un nombre dont la racine carrée est un nombre entier, comme
3 Reconnaître la différence particulière des carrés parfaits."Un carré parfait est un nombre dont la racine carrée est un nombre entier, comme 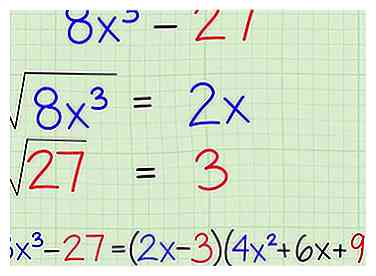 4 Apprenez à décomposer la "différence de cubes parfaits"."Tout comme les carrés parfaits, il s’agit d’une formule simple pour laquelle deux termes cubes sont soustraits. Par exemple,
4 Apprenez à décomposer la "différence de cubes parfaits"."Tout comme les carrés parfaits, il s’agit d’une formule simple pour laquelle deux termes cubes sont soustraits. Par exemple, 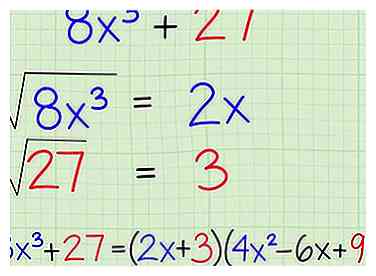 5 Sachez que la somme des cubes parfaits tient aussi dans une formule. Contrairement à la différence des carrés parfaits, vous pouvez facilement trouver des cubes ajoutés, comme
5 Sachez que la somme des cubes parfaits tient aussi dans une formule. Contrairement à la différence des carrés parfaits, vous pouvez facilement trouver des cubes ajoutés, comme