Le graphique d'un polynôme ou d'une fonction révèle de nombreuses caractéristiques qui ne seraient pas claires sans une représentation visuelle. L'une de ces caractéristiques est l'axe de symétrie: une ligne verticale sur un graphique qui divise le graphique en deux images miroir symétriques. Trouver l'axe de symétrie pour un polynôme donné est assez simple. Il existe deux méthodes de base.
Méthode One of Two:
Trouver l'axe de la symétrie pour les polynômes de degré 2
-
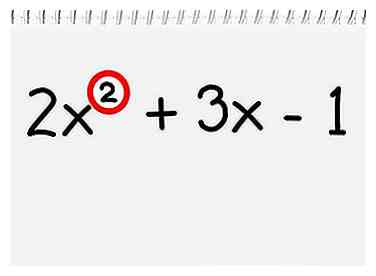 1 Vérifiez le degré de votre polynôme. Le degré (ou «ordre») d'un polynôme est simplement la plus grande valeur d'exposant dans l'expression. Si le degré de votre polynôme est 2 (il n'y a pas d'exposant supérieur à x2), vous pouvez trouver l’axe de symétrie en utilisant cette méthode. Si le degré du polynôme est supérieur à 2, utilisez la méthode 2.
1 Vérifiez le degré de votre polynôme. Le degré (ou «ordre») d'un polynôme est simplement la plus grande valeur d'exposant dans l'expression. Si le degré de votre polynôme est 2 (il n'y a pas d'exposant supérieur à x2), vous pouvez trouver l’axe de symétrie en utilisant cette méthode. Si le degré du polynôme est supérieur à 2, utilisez la méthode 2. - Pour illustrer, prenons, à titre d'exemple, le polynôme 2x2 + 3x - 1. Le présent exposant le plus élevé est le x2, donc c'est un polynôme de second ordre, et vous pouvez utiliser cette première méthode pour trouver l'axe de symétrie.
-
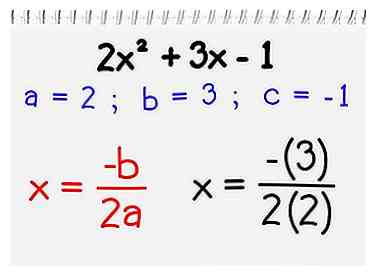 2 Branchez vos numéros dans la formule de l'axe de symétrie. Calculer l'axe de symétrie pour un polynôme de second ordre dans la forme ax2 + bx + c (une parabole), utilisez la formule de base x = -b / 2a.
2 Branchez vos numéros dans la formule de l'axe de symétrie. Calculer l'axe de symétrie pour un polynôme de second ordre dans la forme ax2 + bx + c (une parabole), utilisez la formule de base x = -b / 2a. - Dans l'exemple ci-dessus, a = 2 b = 3 et c = -1. Insérez ces valeurs dans votre formule et vous obtiendrez:
x = -3 / 2 (2) = -3/4.
- Dans l'exemple ci-dessus, a = 2 b = 3 et c = -1. Insérez ces valeurs dans votre formule et vous obtiendrez:
-
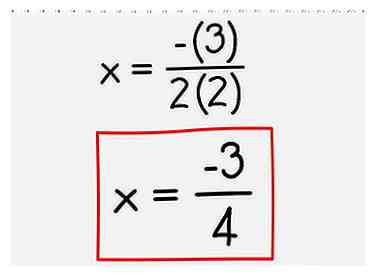 3 Notez l'équation de l'axe de symétrie. La valeur que vous avez calculée avec votre formule d'axe de symétrie est l'interception x de l'axe de symétrie.
3 Notez l'équation de l'axe de symétrie. La valeur que vous avez calculée avec votre formule d'axe de symétrie est l'interception x de l'axe de symétrie. - Dans l'exemple ci-dessus, l'axe de symétrie est -3/4.
Méthode deux sur deux:
Trouver graphiquement l'axe de la symétrie
-
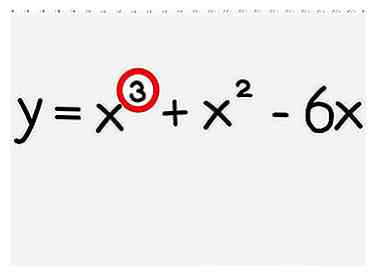 1 Vérifiez le degré de votre polynôme. Le degré (ou «ordre») d'un polynôme est simplement la plus grande valeur d'exposant dans l'expression. Si le degré de votre polynôme est 2 (il n'y a pas d'exposant plus grand que x2), vous pouvez trouver l’axe de symétrie en utilisant la méthode de la formule ci-dessus. Si le degré du polynôme est supérieur à 2, utilisez cette méthode graphique.
1 Vérifiez le degré de votre polynôme. Le degré (ou «ordre») d'un polynôme est simplement la plus grande valeur d'exposant dans l'expression. Si le degré de votre polynôme est 2 (il n'y a pas d'exposant plus grand que x2), vous pouvez trouver l’axe de symétrie en utilisant la méthode de la formule ci-dessus. Si le degré du polynôme est supérieur à 2, utilisez cette méthode graphique. -
 2 Dessine les axes x et y. Faites deux lignes sous la forme d'un signe plus. La ligne horizontale est votre axe des x; la ligne verticale est votre axe y.
2 Dessine les axes x et y. Faites deux lignes sous la forme d'un signe plus. La ligne horizontale est votre axe des x; la ligne verticale est votre axe y. -
 3 Numérotez votre graphique. Marquez les deux axes avec des nombres à intervalles égaux. L'espacement doit être uniforme sur les deux axes.
3 Numérotez votre graphique. Marquez les deux axes avec des nombres à intervalles égaux. L'espacement doit être uniforme sur les deux axes. -
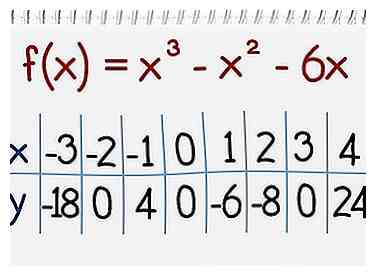 4 Calculez y = f (x) pour chaque x. Prenez votre polynôme ou fonction et calculez les valeurs de f (x) en y mettant toutes les valeurs de x.
4 Calculez y = f (x) pour chaque x. Prenez votre polynôme ou fonction et calculez les valeurs de f (x) en y mettant toutes les valeurs de x. -
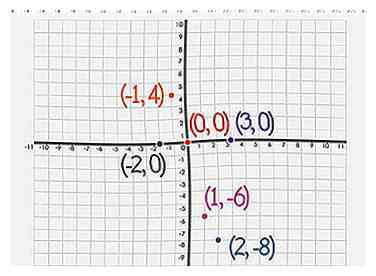 5 Faites un point graphique pour chaque paire. Vous avez maintenant des paires de y = f (x) pour chaque x sur l'axe. Pour chaque paire (x, y), créez un point sur le graphique - verticalement sur l’axe des x et horizontalement sur l’axe des y.
5 Faites un point graphique pour chaque paire. Vous avez maintenant des paires de y = f (x) pour chaque x sur l'axe. Pour chaque paire (x, y), créez un point sur le graphique - verticalement sur l’axe des x et horizontalement sur l’axe des y. -
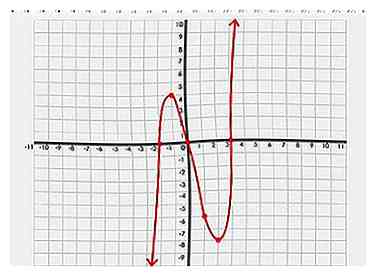 6 Dessine le graphe du polynôme. Une fois que vous avez marqué tous les points du graphique, vous pouvez relier vos points en douceur pour révéler un graphique continu de votre polynôme.
6 Dessine le graphe du polynôme. Une fois que vous avez marqué tous les points du graphique, vous pouvez relier vos points en douceur pour révéler un graphique continu de votre polynôme. -
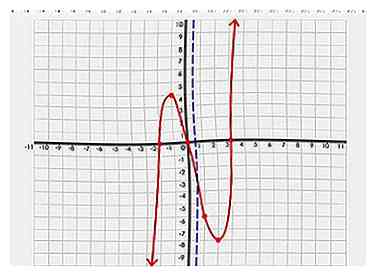 7 Recherchez l'axe de symétrie. Inspectez soigneusement votre graphique. Recherchez un point sur l'axe de telle sorte que, lorsqu'une ligne le traverse, le graphique se divise en deux moitiés égales et en miroir.
7 Recherchez l'axe de symétrie. Inspectez soigneusement votre graphique. Recherchez un point sur l'axe de telle sorte que, lorsqu'une ligne le traverse, le graphique se divise en deux moitiés égales et en miroir. -
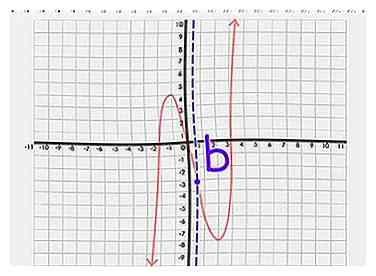 8 Notez l'axe de symétrie. Si vous pouvez trouver un point - appelez-le «b» - sur l'axe des x qui divise le graphique en deux moitiés en miroir, alors ce point, b, est votre axe de symétrie.
8 Notez l'axe de symétrie. Si vous pouvez trouver un point - appelez-le «b» - sur l'axe des x qui divise le graphique en deux moitiés en miroir, alors ce point, b, est votre axe de symétrie.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
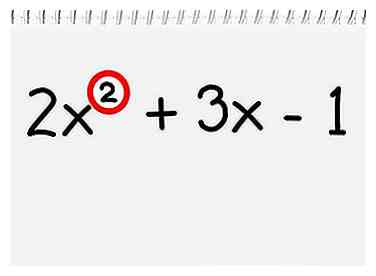 1 Vérifiez le degré de votre polynôme. Le degré (ou «ordre») d'un polynôme est simplement la plus grande valeur d'exposant dans l'expression. Si le degré de votre polynôme est 2 (il n'y a pas d'exposant supérieur à x2), vous pouvez trouver l’axe de symétrie en utilisant cette méthode. Si le degré du polynôme est supérieur à 2, utilisez la méthode 2.
1 Vérifiez le degré de votre polynôme. Le degré (ou «ordre») d'un polynôme est simplement la plus grande valeur d'exposant dans l'expression. Si le degré de votre polynôme est 2 (il n'y a pas d'exposant supérieur à x2), vous pouvez trouver l’axe de symétrie en utilisant cette méthode. Si le degré du polynôme est supérieur à 2, utilisez la méthode 2. 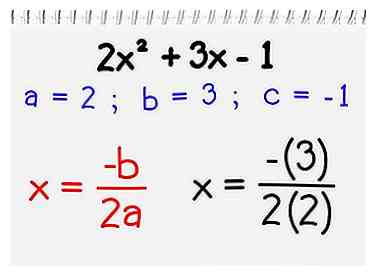 2 Branchez vos numéros dans la formule de l'axe de symétrie. Calculer l'axe de symétrie pour un polynôme de second ordre dans la forme ax2 + bx + c (une parabole), utilisez la formule de base x = -b / 2a.
2 Branchez vos numéros dans la formule de l'axe de symétrie. Calculer l'axe de symétrie pour un polynôme de second ordre dans la forme ax2 + bx + c (une parabole), utilisez la formule de base x = -b / 2a. 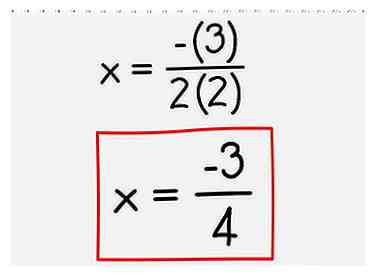 3 Notez l'équation de l'axe de symétrie. La valeur que vous avez calculée avec votre formule d'axe de symétrie est l'interception x de l'axe de symétrie.
3 Notez l'équation de l'axe de symétrie. La valeur que vous avez calculée avec votre formule d'axe de symétrie est l'interception x de l'axe de symétrie. 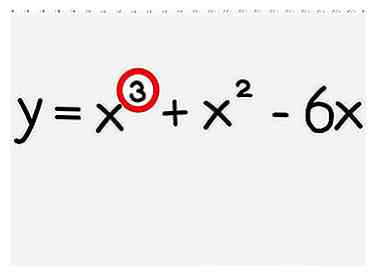 1 Vérifiez le degré de votre polynôme. Le degré (ou «ordre») d'un polynôme est simplement la plus grande valeur d'exposant dans l'expression. Si le degré de votre polynôme est 2 (il n'y a pas d'exposant plus grand que x2), vous pouvez trouver l’axe de symétrie en utilisant la méthode de la formule ci-dessus. Si le degré du polynôme est supérieur à 2, utilisez cette méthode graphique.
1 Vérifiez le degré de votre polynôme. Le degré (ou «ordre») d'un polynôme est simplement la plus grande valeur d'exposant dans l'expression. Si le degré de votre polynôme est 2 (il n'y a pas d'exposant plus grand que x2), vous pouvez trouver l’axe de symétrie en utilisant la méthode de la formule ci-dessus. Si le degré du polynôme est supérieur à 2, utilisez cette méthode graphique.  2 Dessine les axes x et y. Faites deux lignes sous la forme d'un signe plus. La ligne horizontale est votre axe des x; la ligne verticale est votre axe y.
2 Dessine les axes x et y. Faites deux lignes sous la forme d'un signe plus. La ligne horizontale est votre axe des x; la ligne verticale est votre axe y.  3 Numérotez votre graphique. Marquez les deux axes avec des nombres à intervalles égaux. L'espacement doit être uniforme sur les deux axes.
3 Numérotez votre graphique. Marquez les deux axes avec des nombres à intervalles égaux. L'espacement doit être uniforme sur les deux axes. 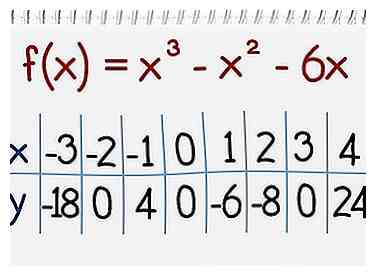 4 Calculez y = f (x) pour chaque x. Prenez votre polynôme ou fonction et calculez les valeurs de f (x) en y mettant toutes les valeurs de x.
4 Calculez y = f (x) pour chaque x. Prenez votre polynôme ou fonction et calculez les valeurs de f (x) en y mettant toutes les valeurs de x.  5 Faites un point graphique pour chaque paire. Vous avez maintenant des paires de y = f (x) pour chaque x sur l'axe. Pour chaque paire (x, y), créez un point sur le graphique - verticalement sur l’axe des x et horizontalement sur l’axe des y.
5 Faites un point graphique pour chaque paire. Vous avez maintenant des paires de y = f (x) pour chaque x sur l'axe. Pour chaque paire (x, y), créez un point sur le graphique - verticalement sur l’axe des x et horizontalement sur l’axe des y.  6 Dessine le graphe du polynôme. Une fois que vous avez marqué tous les points du graphique, vous pouvez relier vos points en douceur pour révéler un graphique continu de votre polynôme.
6 Dessine le graphe du polynôme. Une fois que vous avez marqué tous les points du graphique, vous pouvez relier vos points en douceur pour révéler un graphique continu de votre polynôme.  7 Recherchez l'axe de symétrie. Inspectez soigneusement votre graphique. Recherchez un point sur l'axe de telle sorte que, lorsqu'une ligne le traverse, le graphique se divise en deux moitiés égales et en miroir.
7 Recherchez l'axe de symétrie. Inspectez soigneusement votre graphique. Recherchez un point sur l'axe de telle sorte que, lorsqu'une ligne le traverse, le graphique se divise en deux moitiés égales et en miroir.  8 Notez l'axe de symétrie. Si vous pouvez trouver un point - appelez-le «b» - sur l'axe des x qui divise le graphique en deux moitiés en miroir, alors ce point, b, est votre axe de symétrie.
8 Notez l'axe de symétrie. Si vous pouvez trouver un point - appelez-le «b» - sur l'axe des x qui divise le graphique en deux moitiés en miroir, alors ce point, b, est votre axe de symétrie.