Polynôme signifie "beaucoup de termes" et peut faire référence à une variété d'expressions pouvant inclure des constantes, des variables et des exposants. Par exemple, x - 2 est un polynôme; c'est ainsi 25. Pour trouver le degré d'un polynôme, il suffit de trouver le plus grand exposant du polynôme.[1] Si vous souhaitez trouver le degré d'un polynôme dans diverses situations, suivez ces étapes.
Première partie de trois:
Polynômes avec une variable ou moins
-
 1 Combinez comme termes. Combinez tous les termes similaires dans l'expression afin de pouvoir la simplifier, s'ils ne sont pas déjà combinés. Disons que vous travaillez avec l'expression suivante: 3x2 - 3x4 - 5 + 2x + 2x2 - X. Il suffit de combiner tous les x2, x et termes constants de l'expression pour obtenir 5x2 - 3x4 - 5 + x.
1 Combinez comme termes. Combinez tous les termes similaires dans l'expression afin de pouvoir la simplifier, s'ils ne sont pas déjà combinés. Disons que vous travaillez avec l'expression suivante: 3x2 - 3x4 - 5 + 2x + 2x2 - X. Il suffit de combiner tous les x2, x et termes constants de l'expression pour obtenir 5x2 - 3x4 - 5 + x. -
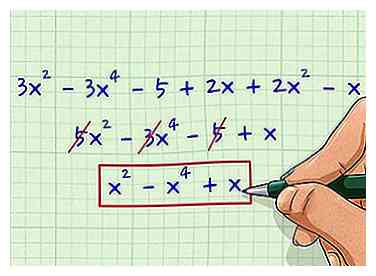 2 Supprimez toutes les constantes et tous les coefficients. Les termes constants sont tous les termes qui ne sont pas attachés à une variable, tels que 3 ou 5. Les coefficients sont les termes qui sont attaché à la variable. Lorsque vous recherchez le degré d'un polynôme, vous pouvez soit ignorer ces termes, soit les supprimer. Par exemple, le coefficient du terme 5x2 serait 5. Le degré est indépendant des coefficients, donc vous n'en avez pas besoin.
2 Supprimez toutes les constantes et tous les coefficients. Les termes constants sont tous les termes qui ne sont pas attachés à une variable, tels que 3 ou 5. Les coefficients sont les termes qui sont attaché à la variable. Lorsque vous recherchez le degré d'un polynôme, vous pouvez soit ignorer ces termes, soit les supprimer. Par exemple, le coefficient du terme 5x2 serait 5. Le degré est indépendant des coefficients, donc vous n'en avez pas besoin. - Travailler avec l'équation 5x2 - 3x4 - 5 + x, vous perdriez les constantes et les coefficients pour obtenir x2 - X4 + x.
-
 3 Mettez les termes dans l'ordre décroissant de leurs exposants. Cela s'appelle aussi mettre le polynôme dans forme standard.[2]. Le terme avec l'exposant le plus élevé devrait être le premier et le terme avec l'exposant le plus bas devrait être le dernier. Cela vous aidera à voir quel terme a l'exposant ayant la plus grande valeur. Dans l'exemple précédent, vous seriez laissé avec
3 Mettez les termes dans l'ordre décroissant de leurs exposants. Cela s'appelle aussi mettre le polynôme dans forme standard.[2]. Le terme avec l'exposant le plus élevé devrait être le premier et le terme avec l'exposant le plus bas devrait être le dernier. Cela vous aidera à voir quel terme a l'exposant ayant la plus grande valeur. Dans l'exemple précédent, vous seriez laissé avec
-X4 + x2 + x. -
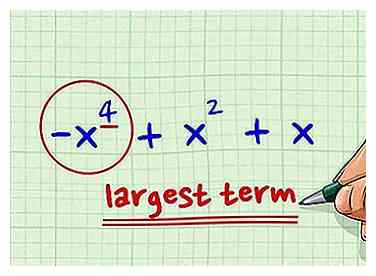 4 Trouvez le pouvoir du plus grand terme. Le pouvoir est simplement le nombre dans l'exposant. Dans l'exemple, -x4 + x2 + x, la puissance du premier terme est 4. Comme vous avez arrangé le polynôme pour placer l'exposant le plus grand en premier, ce sera là que vous trouverez le plus grand terme.
4 Trouvez le pouvoir du plus grand terme. Le pouvoir est simplement le nombre dans l'exposant. Dans l'exemple, -x4 + x2 + x, la puissance du premier terme est 4. Comme vous avez arrangé le polynôme pour placer l'exposant le plus grand en premier, ce sera là que vous trouverez le plus grand terme. -
 5 Identifiez ce nombre comme le degré du polynôme. Vous pouvez simplement écrire le degré du polynôme = 4, ou vous pouvez écrire la réponse sous une forme plus appropriée: deg (3x2 - 3x4 - 5 + 2x + 2x2 - x) = 3. Vous avez tous terminé.[3]
5 Identifiez ce nombre comme le degré du polynôme. Vous pouvez simplement écrire le degré du polynôme = 4, ou vous pouvez écrire la réponse sous une forme plus appropriée: deg (3x2 - 3x4 - 5 + 2x + 2x2 - x) = 3. Vous avez tous terminé.[3] -
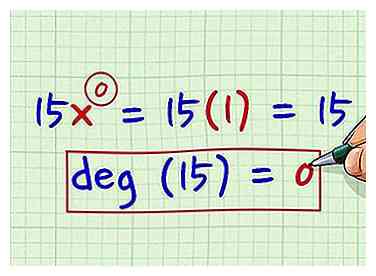 6 Sachez que le degré d'une constante est zéro. Si votre polynôme n'est qu'une constante, telle que 15 ou 55, alors le degré de ce polynôme est vraiment nul. Vous pouvez penser que le terme constant est attaché à une variable au degré 0, ce qui est vraiment 1. Par exemple, si vous avez la constante 15, vous pouvez la considérer comme 15x0, ce qui est vraiment 15 x 1 ou 15. Cela prouve que le degré d'une constante est 0.
6 Sachez que le degré d'une constante est zéro. Si votre polynôme n'est qu'une constante, telle que 15 ou 55, alors le degré de ce polynôme est vraiment nul. Vous pouvez penser que le terme constant est attaché à une variable au degré 0, ce qui est vraiment 1. Par exemple, si vous avez la constante 15, vous pouvez la considérer comme 15x0, ce qui est vraiment 15 x 1 ou 15. Cela prouve que le degré d'une constante est 0.
Deuxième partie de trois:
Polynômes à variables multiples
-
 1 Ecrivez l'expression. Trouver le degré d'un polynôme à variables multiples n'est qu'un peu plus compliqué que de trouver le degré d'un polynôme à une variable. Disons que vous travaillez avec l'expression suivante:
1 Ecrivez l'expression. Trouver le degré d'un polynôme à variables multiples n'est qu'un peu plus compliqué que de trouver le degré d'un polynôme à une variable. Disons que vous travaillez avec l'expression suivante: - X5y3z + 2xy3 + 4x2yz2
-
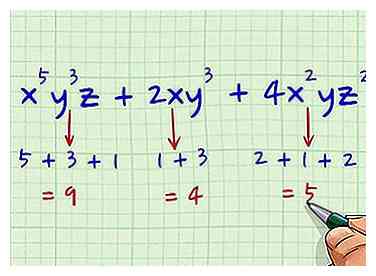 2 Ajoutez le degré de variables dans chaque terme. Additionnez simplement les degrés des variables dans chacun des termes; cela n'a pas d'importance qu'ils soient des variables différentes. Rappelez-vous que le degré d'une variable sans degré écrit, tel que x ou y, est juste un. Voici comment vous le faites pour les trois termes:[4]
2 Ajoutez le degré de variables dans chaque terme. Additionnez simplement les degrés des variables dans chacun des termes; cela n'a pas d'importance qu'ils soient des variables différentes. Rappelez-vous que le degré d'une variable sans degré écrit, tel que x ou y, est juste un. Voici comment vous le faites pour les trois termes:[4] - X5y3z = 5 + 3 + 1 = 9
- 2xy3 = 1 + 3 = 4
- 4x2yz2 = 2 + 1 + 2 = 5
-
 3 Identifiez le plus grand degré de ces termes. Le plus grand degré de ces trois termes est 9, la valeur des valeurs de degré ajoutées au premier terme.
3 Identifiez le plus grand degré de ces termes. Le plus grand degré de ces trois termes est 9, la valeur des valeurs de degré ajoutées au premier terme. -
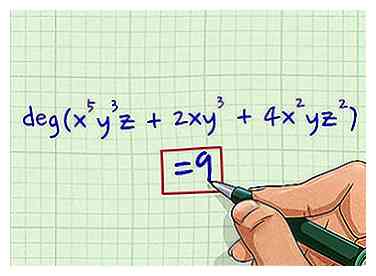 4 Identifiez ce nombre comme le degré du polynôme. 9 est le degré de l'ensemble du polynôme. Vous pouvez écrire la réponse finale comme ceci: deg (x5y3z + 2xy3 + 4x2yz2) = 9.
4 Identifiez ce nombre comme le degré du polynôme. 9 est le degré de l'ensemble du polynôme. Vous pouvez écrire la réponse finale comme ceci: deg (x5y3z + 2xy3 + 4x2yz2) = 9.
Troisième partie de trois:
Expressions rationnelles
-
 1 Notez l'expression. Disons que vous travaillez avec l'expression suivante: (x2 + 1) / (6x -2).[5]
1 Notez l'expression. Disons que vous travaillez avec l'expression suivante: (x2 + 1) / (6x -2).[5] -
 2 Élimine tous les coefficients et constantes. Vous n'aurez pas besoin des coefficients ou des termes constants pour trouver le degré d'un polynôme avec des fractions. Donc, éliminez le 1 du numérateur et le 6 et le 2 du dénominateur. Vous êtes parti avec x2/X.
2 Élimine tous les coefficients et constantes. Vous n'aurez pas besoin des coefficients ou des termes constants pour trouver le degré d'un polynôme avec des fractions. Donc, éliminez le 1 du numérateur et le 6 et le 2 du dénominateur. Vous êtes parti avec x2/X. -
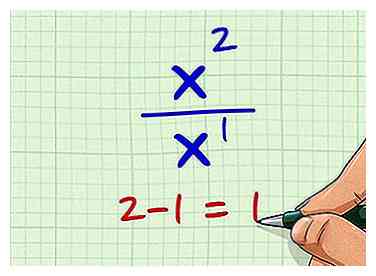 3 Soustrayez le degré de la variable dans le dénominateur du degré de la variable dans le numérateur. Le degré de la variable dans le numérateur est 2 et le degré de la variable dans le dénominateur est 1. Donc, soustrayez 1 de 2. 2-1 = 1.
3 Soustrayez le degré de la variable dans le dénominateur du degré de la variable dans le numérateur. Le degré de la variable dans le numérateur est 2 et le degré de la variable dans le dénominateur est 1. Donc, soustrayez 1 de 2. 2-1 = 1. -
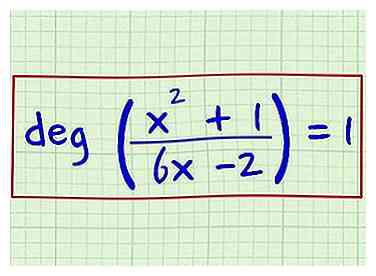 4 Ecrivez le résultat comme votre réponse. Le degré de cette expression rationnelle est 1. Vous pouvez l'écrire comme ceci: deg [(x2 + 1) / (6x -2)] = 1.
4 Ecrivez le résultat comme votre réponse. Le degré de cette expression rationnelle est 1. Vous pouvez l'écrire comme ceci: deg [(x2 + 1) / (6x -2)] = 1.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Combinez comme termes. Combinez tous les termes similaires dans l'expression afin de pouvoir la simplifier, s'ils ne sont pas déjà combinés. Disons que vous travaillez avec l'expression suivante: 3x2 - 3x4 - 5 + 2x + 2x2 - X. Il suffit de combiner tous les x2, x et termes constants de l'expression pour obtenir 5x2 - 3x4 - 5 + x.
1 Combinez comme termes. Combinez tous les termes similaires dans l'expression afin de pouvoir la simplifier, s'ils ne sont pas déjà combinés. Disons que vous travaillez avec l'expression suivante: 3x2 - 3x4 - 5 + 2x + 2x2 - X. Il suffit de combiner tous les x2, x et termes constants de l'expression pour obtenir 5x2 - 3x4 - 5 + x. 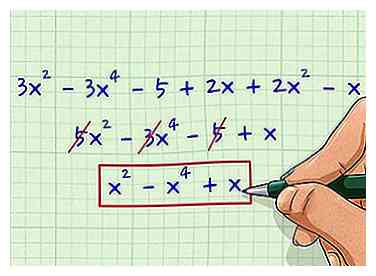 2 Supprimez toutes les constantes et tous les coefficients. Les termes constants sont tous les termes qui ne sont pas attachés à une variable, tels que 3 ou 5. Les coefficients sont les termes qui sont attaché à la variable. Lorsque vous recherchez le degré d'un polynôme, vous pouvez soit ignorer ces termes, soit les supprimer. Par exemple, le coefficient du terme 5x2 serait 5. Le degré est indépendant des coefficients, donc vous n'en avez pas besoin.
2 Supprimez toutes les constantes et tous les coefficients. Les termes constants sont tous les termes qui ne sont pas attachés à une variable, tels que 3 ou 5. Les coefficients sont les termes qui sont attaché à la variable. Lorsque vous recherchez le degré d'un polynôme, vous pouvez soit ignorer ces termes, soit les supprimer. Par exemple, le coefficient du terme 5x2 serait 5. Le degré est indépendant des coefficients, donc vous n'en avez pas besoin.  3 Mettez les termes dans l'ordre décroissant de leurs exposants. Cela s'appelle aussi mettre le polynôme dans forme standard.[2]. Le terme avec l'exposant le plus élevé devrait être le premier et le terme avec l'exposant le plus bas devrait être le dernier. Cela vous aidera à voir quel terme a l'exposant ayant la plus grande valeur. Dans l'exemple précédent, vous seriez laissé avec
3 Mettez les termes dans l'ordre décroissant de leurs exposants. Cela s'appelle aussi mettre le polynôme dans forme standard.[2]. Le terme avec l'exposant le plus élevé devrait être le premier et le terme avec l'exposant le plus bas devrait être le dernier. Cela vous aidera à voir quel terme a l'exposant ayant la plus grande valeur. Dans l'exemple précédent, vous seriez laissé avec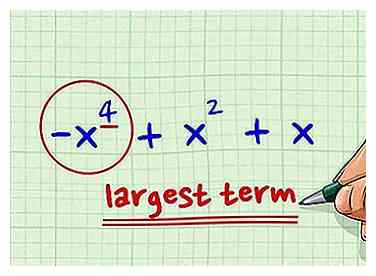 4 Trouvez le pouvoir du plus grand terme. Le pouvoir est simplement le nombre dans l'exposant. Dans l'exemple, -x4 + x2 + x, la puissance du premier terme est 4. Comme vous avez arrangé le polynôme pour placer l'exposant le plus grand en premier, ce sera là que vous trouverez le plus grand terme.
4 Trouvez le pouvoir du plus grand terme. Le pouvoir est simplement le nombre dans l'exposant. Dans l'exemple, -x4 + x2 + x, la puissance du premier terme est 4. Comme vous avez arrangé le polynôme pour placer l'exposant le plus grand en premier, ce sera là que vous trouverez le plus grand terme.  5 Identifiez ce nombre comme le degré du polynôme. Vous pouvez simplement écrire le degré du polynôme = 4, ou vous pouvez écrire la réponse sous une forme plus appropriée: deg (3x2 - 3x4 - 5 + 2x + 2x2 - x) = 3. Vous avez tous terminé.[3]
5 Identifiez ce nombre comme le degré du polynôme. Vous pouvez simplement écrire le degré du polynôme = 4, ou vous pouvez écrire la réponse sous une forme plus appropriée: deg (3x2 - 3x4 - 5 + 2x + 2x2 - x) = 3. Vous avez tous terminé.[3] 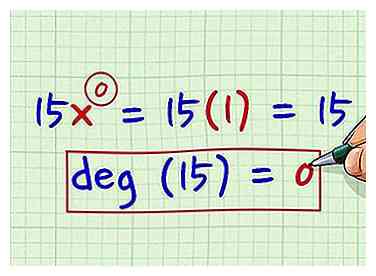 6 Sachez que le degré d'une constante est zéro. Si votre polynôme n'est qu'une constante, telle que 15 ou 55, alors le degré de ce polynôme est vraiment nul. Vous pouvez penser que le terme constant est attaché à une variable au degré 0, ce qui est vraiment 1. Par exemple, si vous avez la constante 15, vous pouvez la considérer comme 15x0, ce qui est vraiment 15 x 1 ou 15. Cela prouve que le degré d'une constante est 0.
6 Sachez que le degré d'une constante est zéro. Si votre polynôme n'est qu'une constante, telle que 15 ou 55, alors le degré de ce polynôme est vraiment nul. Vous pouvez penser que le terme constant est attaché à une variable au degré 0, ce qui est vraiment 1. Par exemple, si vous avez la constante 15, vous pouvez la considérer comme 15x0, ce qui est vraiment 15 x 1 ou 15. Cela prouve que le degré d'une constante est 0.  1 Ecrivez l'expression. Trouver le degré d'un polynôme à variables multiples n'est qu'un peu plus compliqué que de trouver le degré d'un polynôme à une variable. Disons que vous travaillez avec l'expression suivante:
1 Ecrivez l'expression. Trouver le degré d'un polynôme à variables multiples n'est qu'un peu plus compliqué que de trouver le degré d'un polynôme à une variable. Disons que vous travaillez avec l'expression suivante: 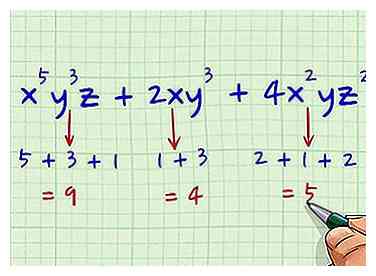 2 Ajoutez le degré de variables dans chaque terme. Additionnez simplement les degrés des variables dans chacun des termes; cela n'a pas d'importance qu'ils soient des variables différentes. Rappelez-vous que le degré d'une variable sans degré écrit, tel que x ou y, est juste un. Voici comment vous le faites pour les trois termes:[4]
2 Ajoutez le degré de variables dans chaque terme. Additionnez simplement les degrés des variables dans chacun des termes; cela n'a pas d'importance qu'ils soient des variables différentes. Rappelez-vous que le degré d'une variable sans degré écrit, tel que x ou y, est juste un. Voici comment vous le faites pour les trois termes:[4]  3 Identifiez le plus grand degré de ces termes. Le plus grand degré de ces trois termes est 9, la valeur des valeurs de degré ajoutées au premier terme.
3 Identifiez le plus grand degré de ces termes. Le plus grand degré de ces trois termes est 9, la valeur des valeurs de degré ajoutées au premier terme. 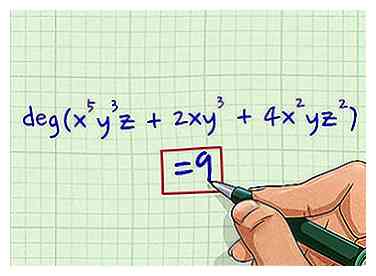 4 Identifiez ce nombre comme le degré du polynôme. 9 est le degré de l'ensemble du polynôme. Vous pouvez écrire la réponse finale comme ceci: deg (x5y3z + 2xy3 + 4x2yz2) = 9.
4 Identifiez ce nombre comme le degré du polynôme. 9 est le degré de l'ensemble du polynôme. Vous pouvez écrire la réponse finale comme ceci: deg (x5y3z + 2xy3 + 4x2yz2) = 9.  1 Notez l'expression. Disons que vous travaillez avec l'expression suivante: (x2 + 1) / (6x -2).[5]
1 Notez l'expression. Disons que vous travaillez avec l'expression suivante: (x2 + 1) / (6x -2).[5]  2 Élimine tous les coefficients et constantes. Vous n'aurez pas besoin des coefficients ou des termes constants pour trouver le degré d'un polynôme avec des fractions. Donc, éliminez le 1 du numérateur et le 6 et le 2 du dénominateur. Vous êtes parti avec x2/X.
2 Élimine tous les coefficients et constantes. Vous n'aurez pas besoin des coefficients ou des termes constants pour trouver le degré d'un polynôme avec des fractions. Donc, éliminez le 1 du numérateur et le 6 et le 2 du dénominateur. Vous êtes parti avec x2/X. 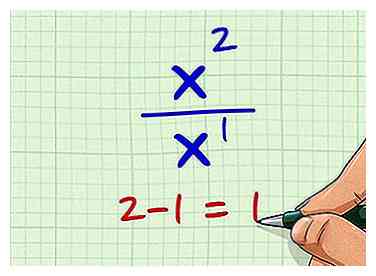 3 Soustrayez le degré de la variable dans le dénominateur du degré de la variable dans le numérateur. Le degré de la variable dans le numérateur est 2 et le degré de la variable dans le dénominateur est 1. Donc, soustrayez 1 de 2. 2-1 = 1.
3 Soustrayez le degré de la variable dans le dénominateur du degré de la variable dans le numérateur. Le degré de la variable dans le numérateur est 2 et le degré de la variable dans le dénominateur est 1. Donc, soustrayez 1 de 2. 2-1 = 1. 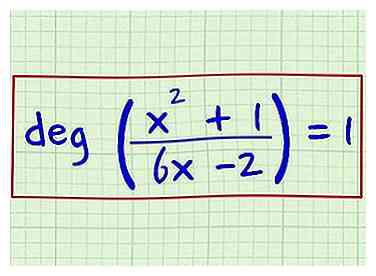 4 Ecrivez le résultat comme votre réponse. Le degré de cette expression rationnelle est 1. Vous pouvez l'écrire comme ceci: deg [(x2 + 1) / (6x -2)] = 1.
4 Ecrivez le résultat comme votre réponse. Le degré de cette expression rationnelle est 1. Vous pouvez l'écrire comme ceci: deg [(x2 + 1) / (6x -2)] = 1.