L'algèbre est une branche des mathématiques qui étudie les nombres en représentant des quantités inconnues avec des variables de lettre, ainsi que les opérations mathématiques qui leur sont appliquées. C'est la porte d'entrée des étudiants vers les mathématiques supérieures et c'est trop souvent une pierre d'achoppement pour eux, pas seulement en termes de scolarité, mais aussi en termes de capacité à entrer dans une bonne université et à étudier pour la carrière souhaitée. L'importance et les pressions de l'algèbre et des mathématiques en général motivent de nombreux parents à chercher des moyens d'aider leurs enfants à se préparer à l'algèbre, sans toujours comprendre les compétences que leurs enfants devraient maîtriser pour être prêts à l'algèbre.
Méthode One of Two:
Détermination de la préparation de votre enfant pour l'algèbre
-
 1 Considérez l'âge de votre enfant. Certains chercheurs en éducation, tels que le Dr Herman Epstein, pensent que le cerveau humain connaît des périodes de développement rapide et des périodes de développement limité, l’une d’entre elles coïncidant avec une poussée de croissance physique entre 14 et 17 ans.
1 Considérez l'âge de votre enfant. Certains chercheurs en éducation, tels que le Dr Herman Epstein, pensent que le cerveau humain connaît des périodes de développement rapide et des périodes de développement limité, l’une d’entre elles coïncidant avec une poussée de croissance physique entre 14 et 17 ans. -
 2 Considérez le niveau de maturité de votre enfant. Votre enfant devrait montrer des compétences générales en résolution de problèmes, être capable de tirer des conclusions du raisonnement logique et être capable d'organiser des projets.
2 Considérez le niveau de maturité de votre enfant. Votre enfant devrait montrer des compétences générales en résolution de problèmes, être capable de tirer des conclusions du raisonnement logique et être capable d'organiser des projets. -
 3 Soyez conscient du programme de mathématiques dans le district scolaire de votre enfant. Historiquement dans les écoles américaines, l'algèbre a été introduite en 9ème ou 10ème année. En raison des pressions politiques résultant en partie de la loi No Child Left Behind, de nombreux districts scolaires ont officiellement introduit l'algèbre en 8e année, avec des concepts préliminaires enseignés en 7e année.
3 Soyez conscient du programme de mathématiques dans le district scolaire de votre enfant. Historiquement dans les écoles américaines, l'algèbre a été introduite en 9ème ou 10ème année. En raison des pressions politiques résultant en partie de la loi No Child Left Behind, de nombreux districts scolaires ont officiellement introduit l'algèbre en 8e année, avec des concepts préliminaires enseignés en 7e année. - Si vous scolarisez votre enfant à la maison, examinez les programmes de plusieurs districts de votre région immédiate pour savoir à quel moment il pourrait être approprié de préparer votre enfant à l’algèbre.
-
 4 Évaluez l'état de préparation de votre enfant pour l'algèbre. Vous pouvez le faire de 1 à 2 façons:
4 Évaluez l'état de préparation de votre enfant pour l'algèbre. Vous pouvez le faire de 1 à 2 façons: - Grâce à un test formel d'algèbre. De nombreux districts scolaires proposent des tests de préparation à l’algèbre afin de placer les élèves dans des filières d’études pour leurs études secondaires. Ces tests sont généralement offerts pendant les années de collège d'un élève. Des organisations telles que College Preparatory Mathematics et Sylvan Learning proposent des tests de préparation à l'algèbre en ligne ou téléchargeables.
- En examinant régulièrement les devoirs de mathématiques de votre enfant. Utilisez les informations présentées sous "Prérequis pour l'algèbre" et comprenez le programme de votre district scolaire pour suivre les progrès de votre enfant dans le développement des compétences préliminaires à l'apprentissage de l'algèbre.
-
 5 Présentez des concepts algébriques à votre enfant. Bon nombre des concepts enseignés en algèbre peuvent être présentés aux enfants plus jeunes s'ils sont effectués d'une manière adaptée à leur âge. Par exemple, vous pouvez introduire le concept de variables en demandant à votre enfant quel nombre ajouté à 6 fait 10.
5 Présentez des concepts algébriques à votre enfant. Bon nombre des concepts enseignés en algèbre peuvent être présentés aux enfants plus jeunes s'ils sont effectués d'une manière adaptée à leur âge. Par exemple, vous pouvez introduire le concept de variables en demandant à votre enfant quel nombre ajouté à 6 fait 10.
Méthode deux sur deux:
Prérequis pour l'algèbre
-
 1 Comprendre et écrire différentes formes numériques. Votre enfant devrait pouvoir lire, écrire, comparer et convertir les formulaires suivants:
1 Comprendre et écrire différentes formes numériques. Votre enfant devrait pouvoir lire, écrire, comparer et convertir les formulaires suivants: - Entiers. Les nombres entiers incluent les nombres de comptage (1, 2, 3, etc., qui sont des entiers positifs), les nombres entiers (0, 1, 2, 3, etc.) et leurs contreparties de valeur négative (inverses additifs, -1, -2, -3, etc.).
- Fractions. Les fractions sont écrites sous la forme d'un nombre (le numérateur) par rapport à un autre (le dénominateur), séparées par une ligne, telle que 1/2. Votre enfant devrait comprendre et identifier les fractions appropriées (qui ont un numérateur plus petit que le dénominateur, tel que 2/3), des fractions impropres (qui ont un numérateur aussi grand ou plus grand que le dénominateur, tel que 3/2), et des nombres mixtes (qui combinent un entier avec une fraction, tel que 1 1/2).
- Décimales. Les décimales sont un autre moyen d'exprimer des valeurs fractionnaires en utilisant un point décimal au lieu d'une barre de fraction. Votre enfant devrait être capable de comprendre la valeur de la décimale (celle-ci étant supérieure à 0,05 car 5 dixièmes est supérieure à 5 centièmes) et être capable de convertir les décimales en fractions et inversement.
- Pourcentages Les pourcentages sont une expression de valeurs numériques sous forme de parties de 100 ("%"). Votre enfant devrait être capable de convertir des pourcentages et des valeurs décimales pour le même numéro.
- Exposants. Les exposants sont des nombres en exposant (augmentés) utilisés pour représenter combien de fois un nombre de base est utilisé comme facteur de multiplication. Ils sont parfois appelés "pouvoirs". Les exposants peuvent aussi être écrits sous la forme de chiffres normaux après un caret (^) lorsque l'exposant n'est pas possible. Votre enfant devrait être capable de convertir des nombres élevés en puissances à leurs valeurs équivalentes, telles que 4 ^ 2 = 16 et 10 ^ 3 = 1000.
- Notation scientifique. La notation scientifique écrit une grande valeur numérique sous la forme d'un nombre décimal multiplié par 10 élevé à une puissance. Le nombre 1,600,000 serait écrit en notation scientifique comme 1,6 x 10 ^ 6.
-
 2 Calculez les nombres sous toutes les formes décrites ci-dessus. Votre enfant devrait être en mesure d'ajouter, de soustraire, de multiplier et de diviser des nombres entiers, des fractions, des décimales, des pourcentages et en notation scientifique, avec certaines des compétences suivantes:
2 Calculez les nombres sous toutes les formes décrites ci-dessus. Votre enfant devrait être en mesure d'ajouter, de soustraire, de multiplier et de diviser des nombres entiers, des fractions, des décimales, des pourcentages et en notation scientifique, avec certaines des compétences suivantes: - Lors de l'ajout ou de la soustraction de fractions, votre enfant devrait être capable de convertir des fractions en des formes équivalentes afin que les deux termes aient le même dénominateur. En multipliant les fractions, votre enfant devrait pouvoir multiplier les numérateurs et les dénominateurs ensemble et réduire le résultat aux termes les plus bas.
- Lorsque vous multipliez les nombres décimaux, votre enfant devrait pouvoir placer le point décimal correctement dans le produit. Lorsque vous divisez une décimale par une autre, votre enfant devrait pouvoir placer correctement le point décimal dans le quotient en déplaçant les points décimaux dans le dividende et diviser le même nombre de points vers la droite pour que le diviseur soit un entier.
-
 3 Être capable de factoriser des nombres. L'affacturage est la capacité d'identifier un nombre comme étant le produit de 2 nombres plus petits (facteurs). Votre enfant devrait pouvoir identifier les facteurs pour un nombre donné et identifier les nombres premiers, qui ne sont divisibles que par 1 et par eux-mêmes. De plus, votre enfant devrait être capable de comprendre et d’effectuer les opérations suivantes:
3 Être capable de factoriser des nombres. L'affacturage est la capacité d'identifier un nombre comme étant le produit de 2 nombres plus petits (facteurs). Votre enfant devrait pouvoir identifier les facteurs pour un nombre donné et identifier les nombres premiers, qui ne sont divisibles que par 1 et par eux-mêmes. De plus, votre enfant devrait être capable de comprendre et d’effectuer les opérations suivantes: - Plus grand facteur commun (GCF). C'est le plus grand nombre pouvant être divisé en deux nombres différents ou plus; Par exemple, le plus grand facteur commun de 12 et 20 est 4 (3 x 4 = 12, 5 x 4 = 20).
- Plus petit multiple commun (LCM). C'est le plus petit nombre qui soit un multiple de 2 nombres différents ou plus; Par exemple, le plus petit multiple commun de 6 et 9 est 18 (3 x 6 = 18, 2 x 9 = 18).
- Prime d'affacturage. C'est être capable d'exprimer un nombre donné en tant que produit de nombres premiers. Par exemple, l'affacturage principal de 60 est 2 x 2 x 3 x 5.
-
 4 Comprendre les ratios, les proportions et les taux. "Ratio" est la comparaison de 2 quantités entre elles, tandis que "proportion" se réfère à la quantité d'un article par rapport à un ensemble. Dans un bol de fruits avec 3 pommes et 5 oranges, le ratio pommes / oranges est de 3: 5 (inscriptible également en 3/5), tandis que la proportion de pommes par rapport à tous les fruits est de 3: 8 (ou 3/8). "Taux" est un rapport de 2 mesures, généralement de différents types, par exemple miles par heure, battements par minute ou cycles par seconde.
4 Comprendre les ratios, les proportions et les taux. "Ratio" est la comparaison de 2 quantités entre elles, tandis que "proportion" se réfère à la quantité d'un article par rapport à un ensemble. Dans un bol de fruits avec 3 pommes et 5 oranges, le ratio pommes / oranges est de 3: 5 (inscriptible également en 3/5), tandis que la proportion de pommes par rapport à tous les fruits est de 3: 8 (ou 3/8). "Taux" est un rapport de 2 mesures, généralement de différents types, par exemple miles par heure, battements par minute ou cycles par seconde. - Les concepts de cotes et de probabilités sont liés aux ratios et aux proportions. La probabilité est un rapport entre le résultat souhaité et tous les résultats possibles. la probabilité d'obtenir des têtes sur un flip de pièces est de 1: 2 (1/2), car une pièce de monnaie peut atteindre la tête ou la queue. La "cote" est le rapport entre le résultat souhaité et les résultats indésirables. les chances d'obtenir des têtes sur un tirage au sort sont de 1: 1.
-
 5 Identifier et dessiner différentes formes géométriques. Ces compétences sont un peu plus indispensables pour les classes de géométrie que pour l’algèbre, mais elles sont liées à la capacité de reconnaître des motifs dans des séquences de nombres et d’autres domaines.
5 Identifier et dessiner différentes formes géométriques. Ces compétences sont un peu plus indispensables pour les classes de géométrie que pour l’algèbre, mais elles sont liées à la capacité de reconnaître des motifs dans des séquences de nombres et d’autres domaines. -
 6 Mesurer et calculer les dimensions et les propriétés de diverses formes géométriques. Votre enfant devrait pouvoir utiliser une règle, un compas et un rapporteur et devrait pouvoir trouver ce qui suit:
6 Mesurer et calculer les dimensions et les propriétés de diverses formes géométriques. Votre enfant devrait pouvoir utiliser une règle, un compas et un rapporteur et devrait pouvoir trouver ce qui suit: - Périmètre: longueur totale de toutes les arêtes d'un objet à deux dimensions.
- Area: La quantité d'espace qu'un objet à deux dimensions prend.
- Volume: quantité d'espace occupée par un objet tridimensionnel.
- Surface: la surface totale de chaque surface d'un objet tridimensionnel.
-
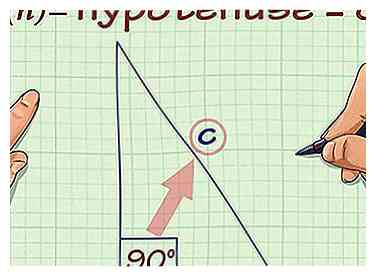 7 Travailler avec le théorème de Pythagore. Le théorème de Pythagore stipule que le carré de la longueur de l'hypoténuse d'un triangle rectangle (le côté opposé à l'angle droit) est égal à la somme des carrés de la longueur des deux autres côtés. Cette compétence permet de préparer votre enfant non seulement à l'algèbre et à la géométrie, mais aussi à la trigonométrie. Votre enfant devrait être capable d'utiliser cette relation pour trouver la longueur de n'importe quel côté d'un triangle rectangle lorsque les 2 autres longueurs sont connues et également déterminer si un triangle est un triangle rectangle si les longueurs des 3 côtés sont données.
7 Travailler avec le théorème de Pythagore. Le théorème de Pythagore stipule que le carré de la longueur de l'hypoténuse d'un triangle rectangle (le côté opposé à l'angle droit) est égal à la somme des carrés de la longueur des deux autres côtés. Cette compétence permet de préparer votre enfant non seulement à l'algèbre et à la géométrie, mais aussi à la trigonométrie. Votre enfant devrait être capable d'utiliser cette relation pour trouver la longueur de n'importe quel côté d'un triangle rectangle lorsque les 2 autres longueurs sont connues et également déterminer si un triangle est un triangle rectangle si les longueurs des 3 côtés sont données. - Parce que trouver la longueur d'un côté inconnu implique de calculer des racines carrées, c'est une opportunité pour votre enfant de développer des compétences en utilisant une calculatrice.
-
 8 Collecter, organiser et présenter des informations pour que les autres puissent le comprendre. Votre enfant doit avoir une compréhension rudimentaire des statistiques (moyenne, médiane, mode et portée) et être capable de lire et de créer des graphiques à barres, des graphiques linéaires et des diagrammes à secteurs, ainsi que de pouvoir tracer des points sur une grille à deux dimensions .
8 Collecter, organiser et présenter des informations pour que les autres puissent le comprendre. Votre enfant doit avoir une compréhension rudimentaire des statistiques (moyenne, médiane, mode et portée) et être capable de lire et de créer des graphiques à barres, des graphiques linéaires et des diagrammes à secteurs, ainsi que de pouvoir tracer des points sur une grille à deux dimensions . -
 9 Comprendre et analyser les patterns. Les modèles qui montrent des gammes constantes de changements (tels que 2, 4, 6, 8, etc.) sont liés à la fois à l'algèbre et à la géométrie. Votre enfant devrait être capable de reconnaître la nature d'un motif et de projeter le prochain nombre dans une séquence numérique.
9 Comprendre et analyser les patterns. Les modèles qui montrent des gammes constantes de changements (tels que 2, 4, 6, 8, etc.) sont liés à la fois à l'algèbre et à la géométrie. Votre enfant devrait être capable de reconnaître la nature d'un motif et de projeter le prochain nombre dans une séquence numérique. -
 10 Comprendre le concept de variables. Les variables sont des quantités inconnues ou variables dans les équations représentées en algèbre par des lettres. Ce concept est souvent introduit plusieurs années avant l’algèbre élémentaire en utilisant des cases ou des blancs pour représenter les quantités inconnues. Votre enfant devrait être capable de comprendre le concept de variables dans ce format et être capable de trouver la valeur de la quantité inconnue.
10 Comprendre le concept de variables. Les variables sont des quantités inconnues ou variables dans les équations représentées en algèbre par des lettres. Ce concept est souvent introduit plusieurs années avant l’algèbre élémentaire en utilisant des cases ou des blancs pour représenter les quantités inconnues. Votre enfant devrait être capable de comprendre le concept de variables dans ce format et être capable de trouver la valeur de la quantité inconnue. -
 11 Représenter des fonctions mathématiques sous forme d'équations et de graphiques. Une fonction est la relation entre un numéro d'entrée et un seul numéro de sortie résultant. (Si une fonction était définie en ajoutant 7 à chaque nombre, 1 serait une entrée et 8 sa sortie correspondante.) Votre enfant devrait être capable de calculer le numéro de sortie pour un numéro d'entrée et une fonction donnés, créer un tableau d'entrées et de sorties valeurs pour une fonction donnée, et construire un graphique linéaire à partir d'un tableau de valeurs d'entrée et de sortie.
11 Représenter des fonctions mathématiques sous forme d'équations et de graphiques. Une fonction est la relation entre un numéro d'entrée et un seul numéro de sortie résultant. (Si une fonction était définie en ajoutant 7 à chaque nombre, 1 serait une entrée et 8 sa sortie correspondante.) Votre enfant devrait être capable de calculer le numéro de sortie pour un numéro d'entrée et une fonction donnés, créer un tableau d'entrées et de sorties valeurs pour une fonction donnée, et construire un graphique linéaire à partir d'un tableau de valeurs d'entrée et de sortie.
 Minotauromaquia
Minotauromaquia
 1 Considérez l'âge de votre enfant. Certains chercheurs en éducation, tels que le Dr Herman Epstein, pensent que le cerveau humain connaît des périodes de développement rapide et des périodes de développement limité, l’une d’entre elles coïncidant avec une poussée de croissance physique entre 14 et 17 ans.
1 Considérez l'âge de votre enfant. Certains chercheurs en éducation, tels que le Dr Herman Epstein, pensent que le cerveau humain connaît des périodes de développement rapide et des périodes de développement limité, l’une d’entre elles coïncidant avec une poussée de croissance physique entre 14 et 17 ans.  2 Considérez le niveau de maturité de votre enfant. Votre enfant devrait montrer des compétences générales en résolution de problèmes, être capable de tirer des conclusions du raisonnement logique et être capable d'organiser des projets.
2 Considérez le niveau de maturité de votre enfant. Votre enfant devrait montrer des compétences générales en résolution de problèmes, être capable de tirer des conclusions du raisonnement logique et être capable d'organiser des projets.  3 Soyez conscient du programme de mathématiques dans le district scolaire de votre enfant. Historiquement dans les écoles américaines, l'algèbre a été introduite en 9ème ou 10ème année. En raison des pressions politiques résultant en partie de la loi No Child Left Behind, de nombreux districts scolaires ont officiellement introduit l'algèbre en 8e année, avec des concepts préliminaires enseignés en 7e année.
3 Soyez conscient du programme de mathématiques dans le district scolaire de votre enfant. Historiquement dans les écoles américaines, l'algèbre a été introduite en 9ème ou 10ème année. En raison des pressions politiques résultant en partie de la loi No Child Left Behind, de nombreux districts scolaires ont officiellement introduit l'algèbre en 8e année, avec des concepts préliminaires enseignés en 7e année.  4 Évaluez l'état de préparation de votre enfant pour l'algèbre. Vous pouvez le faire de 1 à 2 façons:
4 Évaluez l'état de préparation de votre enfant pour l'algèbre. Vous pouvez le faire de 1 à 2 façons:  5 Présentez des concepts algébriques à votre enfant. Bon nombre des concepts enseignés en algèbre peuvent être présentés aux enfants plus jeunes s'ils sont effectués d'une manière adaptée à leur âge. Par exemple, vous pouvez introduire le concept de variables en demandant à votre enfant quel nombre ajouté à 6 fait 10.
5 Présentez des concepts algébriques à votre enfant. Bon nombre des concepts enseignés en algèbre peuvent être présentés aux enfants plus jeunes s'ils sont effectués d'une manière adaptée à leur âge. Par exemple, vous pouvez introduire le concept de variables en demandant à votre enfant quel nombre ajouté à 6 fait 10.  1 Comprendre et écrire différentes formes numériques. Votre enfant devrait pouvoir lire, écrire, comparer et convertir les formulaires suivants:
1 Comprendre et écrire différentes formes numériques. Votre enfant devrait pouvoir lire, écrire, comparer et convertir les formulaires suivants:  2 Calculez les nombres sous toutes les formes décrites ci-dessus. Votre enfant devrait être en mesure d'ajouter, de soustraire, de multiplier et de diviser des nombres entiers, des fractions, des décimales, des pourcentages et en notation scientifique, avec certaines des compétences suivantes:
2 Calculez les nombres sous toutes les formes décrites ci-dessus. Votre enfant devrait être en mesure d'ajouter, de soustraire, de multiplier et de diviser des nombres entiers, des fractions, des décimales, des pourcentages et en notation scientifique, avec certaines des compétences suivantes:  3 Être capable de factoriser des nombres. L'affacturage est la capacité d'identifier un nombre comme étant le produit de 2 nombres plus petits (facteurs). Votre enfant devrait pouvoir identifier les facteurs pour un nombre donné et identifier les nombres premiers, qui ne sont divisibles que par 1 et par eux-mêmes. De plus, votre enfant devrait être capable de comprendre et d’effectuer les opérations suivantes:
3 Être capable de factoriser des nombres. L'affacturage est la capacité d'identifier un nombre comme étant le produit de 2 nombres plus petits (facteurs). Votre enfant devrait pouvoir identifier les facteurs pour un nombre donné et identifier les nombres premiers, qui ne sont divisibles que par 1 et par eux-mêmes. De plus, votre enfant devrait être capable de comprendre et d’effectuer les opérations suivantes:  4 Comprendre les ratios, les proportions et les taux. "Ratio" est la comparaison de 2 quantités entre elles, tandis que "proportion" se réfère à la quantité d'un article par rapport à un ensemble. Dans un bol de fruits avec 3 pommes et 5 oranges, le ratio pommes / oranges est de 3: 5 (inscriptible également en 3/5), tandis que la proportion de pommes par rapport à tous les fruits est de 3: 8 (ou 3/8). "Taux" est un rapport de 2 mesures, généralement de différents types, par exemple miles par heure, battements par minute ou cycles par seconde.
4 Comprendre les ratios, les proportions et les taux. "Ratio" est la comparaison de 2 quantités entre elles, tandis que "proportion" se réfère à la quantité d'un article par rapport à un ensemble. Dans un bol de fruits avec 3 pommes et 5 oranges, le ratio pommes / oranges est de 3: 5 (inscriptible également en 3/5), tandis que la proportion de pommes par rapport à tous les fruits est de 3: 8 (ou 3/8). "Taux" est un rapport de 2 mesures, généralement de différents types, par exemple miles par heure, battements par minute ou cycles par seconde.  5 Identifier et dessiner différentes formes géométriques. Ces compétences sont un peu plus indispensables pour les classes de géométrie que pour l’algèbre, mais elles sont liées à la capacité de reconnaître des motifs dans des séquences de nombres et d’autres domaines.
5 Identifier et dessiner différentes formes géométriques. Ces compétences sont un peu plus indispensables pour les classes de géométrie que pour l’algèbre, mais elles sont liées à la capacité de reconnaître des motifs dans des séquences de nombres et d’autres domaines.  6 Mesurer et calculer les dimensions et les propriétés de diverses formes géométriques. Votre enfant devrait pouvoir utiliser une règle, un compas et un rapporteur et devrait pouvoir trouver ce qui suit:
6 Mesurer et calculer les dimensions et les propriétés de diverses formes géométriques. Votre enfant devrait pouvoir utiliser une règle, un compas et un rapporteur et devrait pouvoir trouver ce qui suit:  7 Travailler avec le théorème de Pythagore. Le théorème de Pythagore stipule que le carré de la longueur de l'hypoténuse d'un triangle rectangle (le côté opposé à l'angle droit) est égal à la somme des carrés de la longueur des deux autres côtés. Cette compétence permet de préparer votre enfant non seulement à l'algèbre et à la géométrie, mais aussi à la trigonométrie. Votre enfant devrait être capable d'utiliser cette relation pour trouver la longueur de n'importe quel côté d'un triangle rectangle lorsque les 2 autres longueurs sont connues et également déterminer si un triangle est un triangle rectangle si les longueurs des 3 côtés sont données.
7 Travailler avec le théorème de Pythagore. Le théorème de Pythagore stipule que le carré de la longueur de l'hypoténuse d'un triangle rectangle (le côté opposé à l'angle droit) est égal à la somme des carrés de la longueur des deux autres côtés. Cette compétence permet de préparer votre enfant non seulement à l'algèbre et à la géométrie, mais aussi à la trigonométrie. Votre enfant devrait être capable d'utiliser cette relation pour trouver la longueur de n'importe quel côté d'un triangle rectangle lorsque les 2 autres longueurs sont connues et également déterminer si un triangle est un triangle rectangle si les longueurs des 3 côtés sont données.  8 Collecter, organiser et présenter des informations pour que les autres puissent le comprendre. Votre enfant doit avoir une compréhension rudimentaire des statistiques (moyenne, médiane, mode et portée) et être capable de lire et de créer des graphiques à barres, des graphiques linéaires et des diagrammes à secteurs, ainsi que de pouvoir tracer des points sur une grille à deux dimensions .
8 Collecter, organiser et présenter des informations pour que les autres puissent le comprendre. Votre enfant doit avoir une compréhension rudimentaire des statistiques (moyenne, médiane, mode et portée) et être capable de lire et de créer des graphiques à barres, des graphiques linéaires et des diagrammes à secteurs, ainsi que de pouvoir tracer des points sur une grille à deux dimensions .  9 Comprendre et analyser les patterns. Les modèles qui montrent des gammes constantes de changements (tels que 2, 4, 6, 8, etc.) sont liés à la fois à l'algèbre et à la géométrie. Votre enfant devrait être capable de reconnaître la nature d'un motif et de projeter le prochain nombre dans une séquence numérique.
9 Comprendre et analyser les patterns. Les modèles qui montrent des gammes constantes de changements (tels que 2, 4, 6, 8, etc.) sont liés à la fois à l'algèbre et à la géométrie. Votre enfant devrait être capable de reconnaître la nature d'un motif et de projeter le prochain nombre dans une séquence numérique.  10 Comprendre le concept de variables. Les variables sont des quantités inconnues ou variables dans les équations représentées en algèbre par des lettres. Ce concept est souvent introduit plusieurs années avant l’algèbre élémentaire en utilisant des cases ou des blancs pour représenter les quantités inconnues. Votre enfant devrait être capable de comprendre le concept de variables dans ce format et être capable de trouver la valeur de la quantité inconnue.
10 Comprendre le concept de variables. Les variables sont des quantités inconnues ou variables dans les équations représentées en algèbre par des lettres. Ce concept est souvent introduit plusieurs années avant l’algèbre élémentaire en utilisant des cases ou des blancs pour représenter les quantités inconnues. Votre enfant devrait être capable de comprendre le concept de variables dans ce format et être capable de trouver la valeur de la quantité inconnue.  11 Représenter des fonctions mathématiques sous forme d'équations et de graphiques. Une fonction est la relation entre un numéro d'entrée et un seul numéro de sortie résultant. (Si une fonction était définie en ajoutant 7 à chaque nombre, 1 serait une entrée et 8 sa sortie correspondante.) Votre enfant devrait être capable de calculer le numéro de sortie pour un numéro d'entrée et une fonction donnés, créer un tableau d'entrées et de sorties valeurs pour une fonction donnée, et construire un graphique linéaire à partir d'un tableau de valeurs d'entrée et de sortie.
11 Représenter des fonctions mathématiques sous forme d'équations et de graphiques. Une fonction est la relation entre un numéro d'entrée et un seul numéro de sortie résultant. (Si une fonction était définie en ajoutant 7 à chaque nombre, 1 serait une entrée et 8 sa sortie correspondante.) Votre enfant devrait être capable de calculer le numéro de sortie pour un numéro d'entrée et une fonction donnés, créer un tableau d'entrées et de sorties valeurs pour une fonction donnée, et construire un graphique linéaire à partir d'un tableau de valeurs d'entrée et de sortie.