Un triangle isocèle est un triangle à deux côtés de même longueur. Ces deux côtés égaux se rejoignent toujours sous le même angle que la base (le troisième côté) et se rencontrent directement au-dessus du milieu de la base. Vous pouvez le tester vous-même avec une règle et deux crayons de même longueur: si vous essayez d'incliner le triangle dans un sens ou dans l'autre, vous ne pourrez pas rencontrer les pointes des crayons. Ces propriétés spéciales du triangle isocèle vous permettent de calculer la surface à partir de quelques informations.
Méthode One of Two:
Trouver la zone à partir des longueurs latérales
-
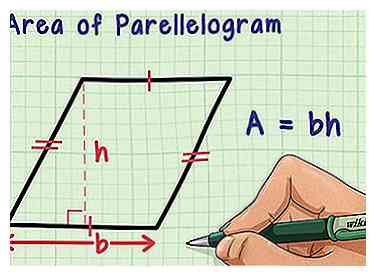 1 Examinez l'aire d'un parallélogramme. Les carrés et les rectangles sont des parallélogrammes, de même que toute forme à quatre côtés avec deux jeux de côtés parallèles. Tous les parallélogrammes ont une formule de surface simple: la surface est égale à la base multipliée par la hauteur, ou A = bh.[1] Si vous placez le parallélogramme à plat sur une surface horizontale, la base correspond à la longueur du côté sur lequel elle se trouve. La hauteur (comme on peut s'y attendre) est la hauteur du sol: la distance entre la base et le côté opposé. Toujours mesurer la hauteur à un angle droit (90 degrés) par rapport à la base.
1 Examinez l'aire d'un parallélogramme. Les carrés et les rectangles sont des parallélogrammes, de même que toute forme à quatre côtés avec deux jeux de côtés parallèles. Tous les parallélogrammes ont une formule de surface simple: la surface est égale à la base multipliée par la hauteur, ou A = bh.[1] Si vous placez le parallélogramme à plat sur une surface horizontale, la base correspond à la longueur du côté sur lequel elle se trouve. La hauteur (comme on peut s'y attendre) est la hauteur du sol: la distance entre la base et le côté opposé. Toujours mesurer la hauteur à un angle droit (90 degrés) par rapport à la base. - Dans les carrés et les rectangles, la hauteur est égale à la longueur d'un côté vertical, puisque ces côtés sont perpendiculaires au sol.
-
 2 Comparez les triangles et les parallélogrammes. Il y a une relation simple entre ces deux formes. Couper un parallélogramme en deux le long de la diagonale, et il se divise en deux triangles égaux. De même, si vous avez deux triangles identiques, vous pouvez toujours les coller ensemble pour créer un parallélogramme. Cela signifie que la zone de tout triangle peut être écrite comme A = ½bh, exactement la moitié de la taille d'un parallélogramme correspondant.
2 Comparez les triangles et les parallélogrammes. Il y a une relation simple entre ces deux formes. Couper un parallélogramme en deux le long de la diagonale, et il se divise en deux triangles égaux. De même, si vous avez deux triangles identiques, vous pouvez toujours les coller ensemble pour créer un parallélogramme. Cela signifie que la zone de tout triangle peut être écrite comme A = ½bh, exactement la moitié de la taille d'un parallélogramme correspondant. -
 3 Trouvez la base du triangle isocèle. Vous avez maintenant la formule, mais que signifient exactement "base" et "hauteur" dans un triangle isocèle? La base est la partie la plus facile: utilisez simplement le troisième côté inégal des isocèles.
3 Trouvez la base du triangle isocèle. Vous avez maintenant la formule, mais que signifient exactement "base" et "hauteur" dans un triangle isocèle? La base est la partie la plus facile: utilisez simplement le troisième côté inégal des isocèles. - Par exemple, si votre triangle isocèle a des côtés de 5 centimètres, 5 cm et 6 cm, utilisez 6 cm comme base.
- Si votre triangle a trois côtés égaux (équilatéraux), vous pouvez choisir n'importe quelle base. Un triangle équilatéral est un type spécial d'isocèles, mais vous pouvez trouver sa zone de la même manière.[2]
-
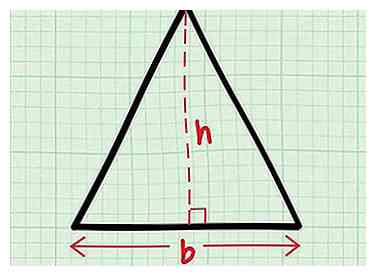 4 Tracez une ligne entre la base et le sommet opposé. Assurez-vous que la ligne frappe la base à angle droit. La longueur de cette ligne correspond à la hauteur de votre triangle. h. Une fois que vous avez calculé la valeur de h, vous pourrez trouver la zone.
4 Tracez une ligne entre la base et le sommet opposé. Assurez-vous que la ligne frappe la base à angle droit. La longueur de cette ligne correspond à la hauteur de votre triangle. h. Une fois que vous avez calculé la valeur de h, vous pourrez trouver la zone. - Dans un triangle isocèle, cette ligne frappera toujours la base à son point médian exact.
-
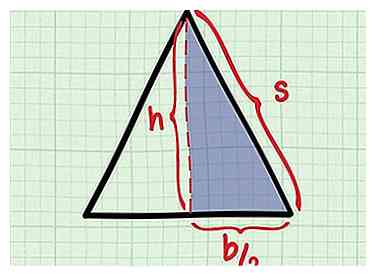 5 Regardez la moitié de votre triangle isocèle. Notez que la ligne de hauteur a divisé votre triangle isocèle en deux triangles droits identiques. Regardez l'un d'eux et identifiez les trois côtés:
5 Regardez la moitié de votre triangle isocèle. Notez que la ligne de hauteur a divisé votre triangle isocèle en deux triangles droits identiques. Regardez l'un d'eux et identifiez les trois côtés: - L'un des petits côtés est égal à la moitié de la base: .
- L'autre petit côté est la hauteur, h.
- L'hypoténuse du triangle rectangle est l'un des deux côtés égaux des isocèles. Appelons ça s.
-
 6 Mettre en place le théorème de Pythagore. Chaque fois que vous connaissez les deux côtés d'un triangle rectangle et que vous voulez trouver le troisième, vous pouvez utiliser le théorème de Pythagore: (côté 1)2 + (côté 2)2 = (hypoténuse)2 Remplacez les variables que nous utilisons pour ce problème pour obtenir .
6 Mettre en place le théorème de Pythagore. Chaque fois que vous connaissez les deux côtés d'un triangle rectangle et que vous voulez trouver le troisième, vous pouvez utiliser le théorème de Pythagore: (côté 1)2 + (côté 2)2 = (hypoténuse)2 Remplacez les variables que nous utilisons pour ce problème pour obtenir . - Vous avez probablement appris le théorème de Pythagore comme . L'écrire comme "côtés" et "hypoténuse" empêche toute confusion avec les variables de votre triangle.
-
 7 Résoudre pour h. Rappelez-vous que la formule de zone utilise b et h, mais vous ne connaissez pas la valeur de h encore. Réorganiser la formule à résoudre h:
7 Résoudre pour h. Rappelez-vous que la formule de zone utilise b et h, mais vous ne connaissez pas la valeur de h encore. Réorganiser la formule à résoudre h: -
.
-
-
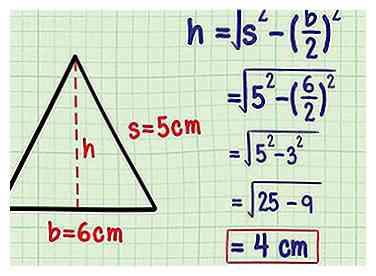 8 Branchez les valeurs de votre triangle pour trouver h. Maintenant que vous connaissez cette formule, vous pouvez l'utiliser pour tout triangle isocèle où vous connaissez les côtés. Il suffit de brancher la longueur de la base pour b et la longueur de l'un des côtés égaux pour s, puis calculer la valeur de h.
8 Branchez les valeurs de votre triangle pour trouver h. Maintenant que vous connaissez cette formule, vous pouvez l'utiliser pour tout triangle isocèle où vous connaissez les côtés. Il suffit de brancher la longueur de la base pour b et la longueur de l'un des côtés égaux pour s, puis calculer la valeur de h. - Par exemple, vous avez un triangle isocèle avec des côtés de 5 cm, 5 cm et 6 cm. b = 6 et s = 5.
- Remplacez-les par votre formule:
cm.
-
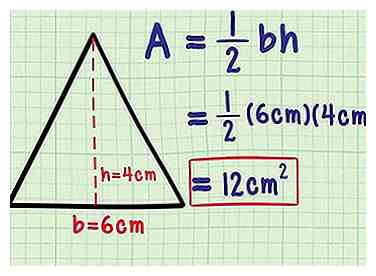 9 Branchez la base et la hauteur dans la formule de votre région. Vous avez maintenant ce dont vous avez besoin pour utiliser la formule depuis le début de cette section: Area = ½bh. Il suffit de brancher les valeurs que vous avez trouvées pour b et h dans cette formule et de calculer la réponse. N'oubliez pas d'écrire votre réponse en termes d'unités carrées.
9 Branchez la base et la hauteur dans la formule de votre région. Vous avez maintenant ce dont vous avez besoin pour utiliser la formule depuis le début de cette section: Area = ½bh. Il suffit de brancher les valeurs que vous avez trouvées pour b et h dans cette formule et de calculer la réponse. N'oubliez pas d'écrire votre réponse en termes d'unités carrées. - Pour continuer l’exemple, le triangle 5-5-6 avait une base de 6 cm et une hauteur de 4 cm.
- A = ½bh
A = ½ (6cm) (4cm)
A = 12cm2.
-
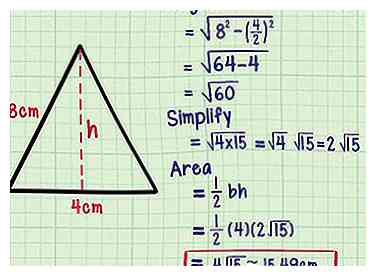 10 Essayez un exemple plus difficile. La plupart des triangles isocèles sont plus difficiles à utiliser que le dernier exemple. La hauteur contient souvent une racine carrée qui ne simplifie pas en un entier. Si cela se produit, laissez la hauteur comme une racine carrée dans sa forme la plus simple. Voici un exemple:
10 Essayez un exemple plus difficile. La plupart des triangles isocèles sont plus difficiles à utiliser que le dernier exemple. La hauteur contient souvent une racine carrée qui ne simplifie pas en un entier. Si cela se produit, laissez la hauteur comme une racine carrée dans sa forme la plus simple. Voici un exemple: - Quelle est l'aire d'un triangle avec des côtés de 8 cm, 8 cm et 4 cm?
- Laissez le côté inégal, 4 cm, être la base b.
- La hauteur
- Simplifiez la racine carrée en trouvant des facteurs:
- Région
- Laissez cette réponse telle quelle ou entrez-la dans une calculatrice pour trouver une estimation décimale (environ 15,49 centimètres carrés).
Méthode deux sur deux:
Utilisation de la trigonométrie
-
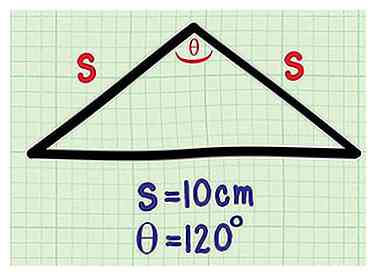 1 Commencez par un côté et un angle. Si vous connaissez la trigonométrie, vous pouvez trouver l'aire d'un triangle isocèle même si vous ne connaissez pas la longueur de l'un de ses côtés. Voici un exemple de problème où vous ne connaissez que les éléments suivants:[3]
1 Commencez par un côté et un angle. Si vous connaissez la trigonométrie, vous pouvez trouver l'aire d'un triangle isocèle même si vous ne connaissez pas la longueur de l'un de ses côtés. Voici un exemple de problème où vous ne connaissez que les éléments suivants:[3] - La durée s des deux côtés égaux est de 10 cm.
- L'angle θ entre les deux côtés égaux est de 120 degrés.
-
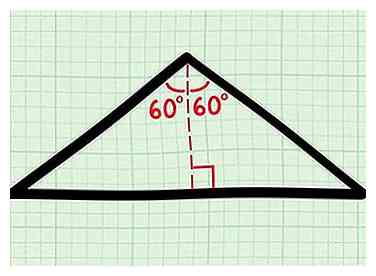 2 Divisez les isocèles en deux triangles droits. Tracez une ligne du sommet entre les deux côtés égaux, qui frappe la base à un angle droit. Vous avez maintenant deux triangles égaux à droite.
2 Divisez les isocèles en deux triangles droits. Tracez une ligne du sommet entre les deux côtés égaux, qui frappe la base à un angle droit. Vous avez maintenant deux triangles égaux à droite. - Cette ligne divise parfaitement θ en deux. Chaque triangle rectangle a un angle de ½θ, ou dans ce cas (½) (120) = 60 degrés.
-
 3 Utilisez la trigonométrie pour trouver la valeur de h. Maintenant que vous avez un triangle rectangle, vous pouvez utiliser les fonctions trigonométriques sinus, cosinus et tangente. Dans l'exemple de problème, vous connaissez l'hypoténuse et vous voulez trouver la valeur de h, le côté adjacent à l'angle connu. Utilisez le fait que cosinus = adjacent / hypoténuse à résoudre pour h:
3 Utilisez la trigonométrie pour trouver la valeur de h. Maintenant que vous avez un triangle rectangle, vous pouvez utiliser les fonctions trigonométriques sinus, cosinus et tangente. Dans l'exemple de problème, vous connaissez l'hypoténuse et vous voulez trouver la valeur de h, le côté adjacent à l'angle connu. Utilisez le fait que cosinus = adjacent / hypoténuse à résoudre pour h: - cos (θ / 2) = h / s
- cos (60º) = h / 10
- h = 10cos (60º)
-
 4 Trouvez la valeur du côté restant. Il reste un côté inconnu du triangle rectangle, que vous pouvez appeler X. Résoudre pour cela en utilisant la définition sinus = opposé / hypoténuse:
4 Trouvez la valeur du côté restant. Il reste un côté inconnu du triangle rectangle, que vous pouvez appeler X. Résoudre pour cela en utilisant la définition sinus = opposé / hypoténuse: - sin (θ / 2) = x / s
- péché (60º) = x / 10
- x = 10sin (60º)
-
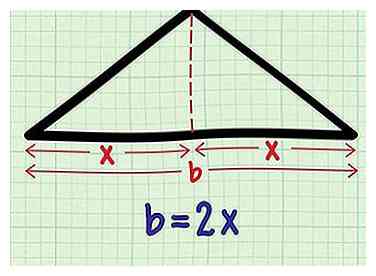 5 Reliez x à la base du triangle isocèle. Vous pouvez maintenant effectuer un zoom arrière sur le triangle isocèle principal. Sa base totale b est égal à 2X, puisqu'il était divisé en deux segments d'une longueur de X.
5 Reliez x à la base du triangle isocèle. Vous pouvez maintenant effectuer un zoom arrière sur le triangle isocèle principal. Sa base totale b est égal à 2X, puisqu'il était divisé en deux segments d'une longueur de X. -
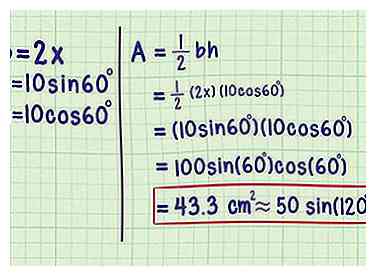 6 Branchez vos valeurs pour h et b dans la formule de base. Maintenant que vous connaissez la base et la hauteur, vous pouvez vous fier à la formule standard A = ½bh:
6 Branchez vos valeurs pour h et b dans la formule de base. Maintenant que vous connaissez la base et la hauteur, vous pouvez vous fier à la formule standard A = ½bh: -
- Vous pouvez entrer ceci dans une calculatrice (définie en degrés), ce qui vous donne une réponse d'environ 43,3 centimètres carrés. Alternativement, utiliser les propriétés de la trigonométrie pour le simplifier à A = 50sin (120º).
-
-
 7 Transformez cela en une formule universelle. Maintenant que vous savez comment cela est résolu, vous pouvez compter sur la formule générale sans passer par le processus complet à chaque fois. Voici ce que vous obtenez si vous répétez ce processus sans utiliser de valeurs spécifiques (et en simplifiant l'utilisation des propriétés de la trigonométrie):[4]
7 Transformez cela en une formule universelle. Maintenant que vous savez comment cela est résolu, vous pouvez compter sur la formule générale sans passer par le processus complet à chaque fois. Voici ce que vous obtenez si vous répétez ce processus sans utiliser de valeurs spécifiques (et en simplifiant l'utilisation des propriétés de la trigonométrie):[4] - s est la longueur de l'un des deux côtés égaux.
- θ est l'angle entre les deux côtés égaux.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Examinez l'aire d'un parallélogramme. Les carrés et les rectangles sont des parallélogrammes, de même que toute forme à quatre côtés avec deux jeux de côtés parallèles. Tous les parallélogrammes ont une formule de surface simple: la surface est égale à la base multipliée par la hauteur, ou A = bh.[1] Si vous placez le parallélogramme à plat sur une surface horizontale, la base correspond à la longueur du côté sur lequel elle se trouve. La hauteur (comme on peut s'y attendre) est la hauteur du sol: la distance entre la base et le côté opposé. Toujours mesurer la hauteur à un angle droit (90 degrés) par rapport à la base.
1 Examinez l'aire d'un parallélogramme. Les carrés et les rectangles sont des parallélogrammes, de même que toute forme à quatre côtés avec deux jeux de côtés parallèles. Tous les parallélogrammes ont une formule de surface simple: la surface est égale à la base multipliée par la hauteur, ou A = bh.[1] Si vous placez le parallélogramme à plat sur une surface horizontale, la base correspond à la longueur du côté sur lequel elle se trouve. La hauteur (comme on peut s'y attendre) est la hauteur du sol: la distance entre la base et le côté opposé. Toujours mesurer la hauteur à un angle droit (90 degrés) par rapport à la base.  2 Comparez les triangles et les parallélogrammes. Il y a une relation simple entre ces deux formes. Couper un parallélogramme en deux le long de la diagonale, et il se divise en deux triangles égaux. De même, si vous avez deux triangles identiques, vous pouvez toujours les coller ensemble pour créer un parallélogramme. Cela signifie que la zone de tout triangle peut être écrite comme A = ½bh, exactement la moitié de la taille d'un parallélogramme correspondant.
2 Comparez les triangles et les parallélogrammes. Il y a une relation simple entre ces deux formes. Couper un parallélogramme en deux le long de la diagonale, et il se divise en deux triangles égaux. De même, si vous avez deux triangles identiques, vous pouvez toujours les coller ensemble pour créer un parallélogramme. Cela signifie que la zone de tout triangle peut être écrite comme A = ½bh, exactement la moitié de la taille d'un parallélogramme correspondant.  3 Trouvez la base du triangle isocèle. Vous avez maintenant la formule, mais que signifient exactement "base" et "hauteur" dans un triangle isocèle? La base est la partie la plus facile: utilisez simplement le troisième côté inégal des isocèles.
3 Trouvez la base du triangle isocèle. Vous avez maintenant la formule, mais que signifient exactement "base" et "hauteur" dans un triangle isocèle? La base est la partie la plus facile: utilisez simplement le troisième côté inégal des isocèles.  4 Tracez une ligne entre la base et le sommet opposé. Assurez-vous que la ligne frappe la base à angle droit. La longueur de cette ligne correspond à la hauteur de votre triangle. h. Une fois que vous avez calculé la valeur de h, vous pourrez trouver la zone.
4 Tracez une ligne entre la base et le sommet opposé. Assurez-vous que la ligne frappe la base à angle droit. La longueur de cette ligne correspond à la hauteur de votre triangle. h. Une fois que vous avez calculé la valeur de h, vous pourrez trouver la zone.  5 Regardez la moitié de votre triangle isocèle. Notez que la ligne de hauteur a divisé votre triangle isocèle en deux triangles droits identiques. Regardez l'un d'eux et identifiez les trois côtés:
5 Regardez la moitié de votre triangle isocèle. Notez que la ligne de hauteur a divisé votre triangle isocèle en deux triangles droits identiques. Regardez l'un d'eux et identifiez les trois côtés:  6 Mettre en place le théorème de Pythagore. Chaque fois que vous connaissez les deux côtés d'un triangle rectangle et que vous voulez trouver le troisième, vous pouvez utiliser le théorème de Pythagore: (côté 1)2 + (côté 2)2 = (hypoténuse)2 Remplacez les variables que nous utilisons pour ce problème pour obtenir
6 Mettre en place le théorème de Pythagore. Chaque fois que vous connaissez les deux côtés d'un triangle rectangle et que vous voulez trouver le troisième, vous pouvez utiliser le théorème de Pythagore: (côté 1)2 + (côté 2)2 = (hypoténuse)2 Remplacez les variables que nous utilisons pour ce problème pour obtenir  7 Résoudre pour h. Rappelez-vous que la formule de zone utilise b et h, mais vous ne connaissez pas la valeur de h encore. Réorganiser la formule à résoudre h:
7 Résoudre pour h. Rappelez-vous que la formule de zone utilise b et h, mais vous ne connaissez pas la valeur de h encore. Réorganiser la formule à résoudre h:  8 Branchez les valeurs de votre triangle pour trouver h. Maintenant que vous connaissez cette formule, vous pouvez l'utiliser pour tout triangle isocèle où vous connaissez les côtés. Il suffit de brancher la longueur de la base pour b et la longueur de l'un des côtés égaux pour s, puis calculer la valeur de h.
8 Branchez les valeurs de votre triangle pour trouver h. Maintenant que vous connaissez cette formule, vous pouvez l'utiliser pour tout triangle isocèle où vous connaissez les côtés. Il suffit de brancher la longueur de la base pour b et la longueur de l'un des côtés égaux pour s, puis calculer la valeur de h.  9 Branchez la base et la hauteur dans la formule de votre région. Vous avez maintenant ce dont vous avez besoin pour utiliser la formule depuis le début de cette section: Area = ½bh. Il suffit de brancher les valeurs que vous avez trouvées pour b et h dans cette formule et de calculer la réponse. N'oubliez pas d'écrire votre réponse en termes d'unités carrées.
9 Branchez la base et la hauteur dans la formule de votre région. Vous avez maintenant ce dont vous avez besoin pour utiliser la formule depuis le début de cette section: Area = ½bh. Il suffit de brancher les valeurs que vous avez trouvées pour b et h dans cette formule et de calculer la réponse. N'oubliez pas d'écrire votre réponse en termes d'unités carrées.  10 Essayez un exemple plus difficile. La plupart des triangles isocèles sont plus difficiles à utiliser que le dernier exemple. La hauteur contient souvent une racine carrée qui ne simplifie pas en un entier. Si cela se produit, laissez la hauteur comme une racine carrée dans sa forme la plus simple. Voici un exemple:
10 Essayez un exemple plus difficile. La plupart des triangles isocèles sont plus difficiles à utiliser que le dernier exemple. La hauteur contient souvent une racine carrée qui ne simplifie pas en un entier. Si cela se produit, laissez la hauteur comme une racine carrée dans sa forme la plus simple. Voici un exemple:  1 Commencez par un côté et un angle. Si vous connaissez la trigonométrie, vous pouvez trouver l'aire d'un triangle isocèle même si vous ne connaissez pas la longueur de l'un de ses côtés. Voici un exemple de problème où vous ne connaissez que les éléments suivants:[3]
1 Commencez par un côté et un angle. Si vous connaissez la trigonométrie, vous pouvez trouver l'aire d'un triangle isocèle même si vous ne connaissez pas la longueur de l'un de ses côtés. Voici un exemple de problème où vous ne connaissez que les éléments suivants:[3]  2 Divisez les isocèles en deux triangles droits. Tracez une ligne du sommet entre les deux côtés égaux, qui frappe la base à un angle droit. Vous avez maintenant deux triangles égaux à droite.
2 Divisez les isocèles en deux triangles droits. Tracez une ligne du sommet entre les deux côtés égaux, qui frappe la base à un angle droit. Vous avez maintenant deux triangles égaux à droite.  3 Utilisez la trigonométrie pour trouver la valeur de h. Maintenant que vous avez un triangle rectangle, vous pouvez utiliser les fonctions trigonométriques sinus, cosinus et tangente. Dans l'exemple de problème, vous connaissez l'hypoténuse et vous voulez trouver la valeur de h, le côté adjacent à l'angle connu. Utilisez le fait que cosinus = adjacent / hypoténuse à résoudre pour h:
3 Utilisez la trigonométrie pour trouver la valeur de h. Maintenant que vous avez un triangle rectangle, vous pouvez utiliser les fonctions trigonométriques sinus, cosinus et tangente. Dans l'exemple de problème, vous connaissez l'hypoténuse et vous voulez trouver la valeur de h, le côté adjacent à l'angle connu. Utilisez le fait que cosinus = adjacent / hypoténuse à résoudre pour h:  4 Trouvez la valeur du côté restant. Il reste un côté inconnu du triangle rectangle, que vous pouvez appeler X. Résoudre pour cela en utilisant la définition sinus = opposé / hypoténuse:
4 Trouvez la valeur du côté restant. Il reste un côté inconnu du triangle rectangle, que vous pouvez appeler X. Résoudre pour cela en utilisant la définition sinus = opposé / hypoténuse:  5 Reliez x à la base du triangle isocèle. Vous pouvez maintenant effectuer un zoom arrière sur le triangle isocèle principal. Sa base totale b est égal à 2X, puisqu'il était divisé en deux segments d'une longueur de X.
5 Reliez x à la base du triangle isocèle. Vous pouvez maintenant effectuer un zoom arrière sur le triangle isocèle principal. Sa base totale b est égal à 2X, puisqu'il était divisé en deux segments d'une longueur de X. 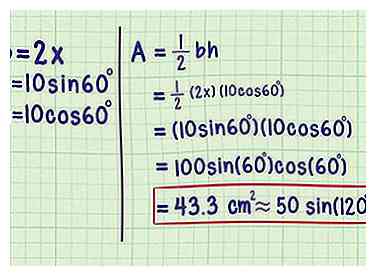 6 Branchez vos valeurs pour h et b dans la formule de base. Maintenant que vous connaissez la base et la hauteur, vous pouvez vous fier à la formule standard A = ½bh:
6 Branchez vos valeurs pour h et b dans la formule de base. Maintenant que vous connaissez la base et la hauteur, vous pouvez vous fier à la formule standard A = ½bh:  7 Transformez cela en une formule universelle. Maintenant que vous savez comment cela est résolu, vous pouvez compter sur la formule générale sans passer par le processus complet à chaque fois. Voici ce que vous obtenez si vous répétez ce processus sans utiliser de valeurs spécifiques (et en simplifiant l'utilisation des propriétés de la trigonométrie):[4]
7 Transformez cela en une formule universelle. Maintenant que vous savez comment cela est résolu, vous pouvez compter sur la formule générale sans passer par le processus complet à chaque fois. Voici ce que vous obtenez si vous répétez ce processus sans utiliser de valeurs spécifiques (et en simplifiant l'utilisation des propriétés de la trigonométrie):[4]