Un pentagone est un polygone à cinq côtés droits. Presque tous les problèmes que vous rencontrerez en cours de maths couvriront les pentagones réguliers, avec cinq côtés égaux. Il existe deux méthodes courantes pour trouver la zone, en fonction de la quantité d’informations dont vous disposez.
Méthode One of Three:
Trouver la zone du côté Longueur et apothème
-
 1 Commencez par la longueur du côté et l'apothème. Cette méthode fonctionne pour les pentagones réguliers, avec cinq côtés égaux. Outre la longueur du côté, vous aurez besoin du "apothème" du pentagone. L'apothème est la ligne allant du centre du pentagone à un côté, coupant le côté à 90 ° à angle droit.
1 Commencez par la longueur du côté et l'apothème. Cette méthode fonctionne pour les pentagones réguliers, avec cinq côtés égaux. Outre la longueur du côté, vous aurez besoin du "apothème" du pentagone. L'apothème est la ligne allant du centre du pentagone à un côté, coupant le côté à 90 ° à angle droit. - Ne confondez pas l'apothème avec le rayon, qui touche un coin (sommet) au lieu d'un point médian. Si vous ne connaissez que la longueur et le rayon du côté, passez à la méthode suivante.
- Nous utiliserons un exemple de pentagone avec une longueur de côté 3 unités et apothème 2 unités.
-
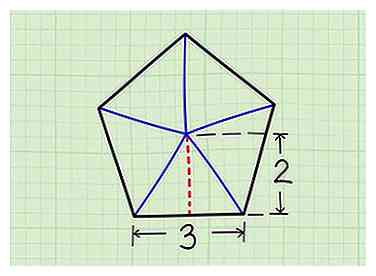 2 Divisez le pentagone en cinq triangles. Tracez cinq lignes à partir du centre du pentagone, menant à chaque sommet (coin). Vous avez maintenant cinq triangles.
2 Divisez le pentagone en cinq triangles. Tracez cinq lignes à partir du centre du pentagone, menant à chaque sommet (coin). Vous avez maintenant cinq triangles. -
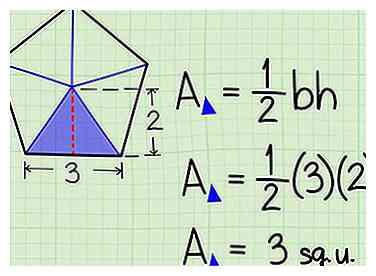 3 Calculez l'aire d'un triangle. Chaque triangle a un base égal au côté du pentagone. Il a aussi un la taille égal à l'apothème du pentagone. (Rappelez-vous que la hauteur d'un triangle va d'un sommet à l'autre, à angle droit.) Pour déterminer l'aire d'un triangle, calculez simplement ½ x base x hauteur.
3 Calculez l'aire d'un triangle. Chaque triangle a un base égal au côté du pentagone. Il a aussi un la taille égal à l'apothème du pentagone. (Rappelez-vous que la hauteur d'un triangle va d'un sommet à l'autre, à angle droit.) Pour déterminer l'aire d'un triangle, calculez simplement ½ x base x hauteur. - Dans notre exemple, zone de triangle = ½ x 3 x 2 = 3 unités carrées.
-
 4 Multipliez par cinq pour trouver la superficie totale. Nous avons divisé le pentagone en cinq triangles égaux. Pour trouver la surface totale, multipliez simplement l'aire d'un triangle par cinq.
4 Multipliez par cinq pour trouver la superficie totale. Nous avons divisé le pentagone en cinq triangles égaux. Pour trouver la surface totale, multipliez simplement l'aire d'un triangle par cinq. - Dans notre exemple, A (pentagone total) = 5 x A (triangle) = 5 x 3 = 15 unités carrées.
Méthode deux sur trois:
Trouver la zone à partir de la longueur latérale
-
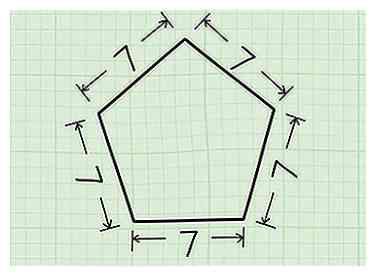 1 Commencez avec juste la longueur du côté. Cette méthode ne fonctionne que pour les pentagones ordinaires, qui ont cinq côtés de même longueur.
1 Commencez avec juste la longueur du côté. Cette méthode ne fonctionne que pour les pentagones ordinaires, qui ont cinq côtés de même longueur. - Dans cet exemple, nous utiliserons un pentagone avec une longueur de côté 7 unités.
-
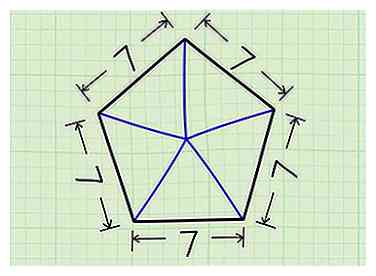 2 Divisez le pentagone en cinq triangles. Tracez une ligne du centre du pentagone à n'importe quel sommet. Répétez cette opération pour chaque sommet. Vous avez maintenant cinq triangles, chacun de la même taille.
2 Divisez le pentagone en cinq triangles. Tracez une ligne du centre du pentagone à n'importe quel sommet. Répétez cette opération pour chaque sommet. Vous avez maintenant cinq triangles, chacun de la même taille. -
 3 Diviser un triangle en deux. Tracez une ligne du centre du pentagone à la base d'un triangle. Cette ligne devrait frapper la base à un angle droit de 90 °, en divisant le triangle en deux triangles plus petits et égaux.
3 Diviser un triangle en deux. Tracez une ligne du centre du pentagone à la base d'un triangle. Cette ligne devrait frapper la base à un angle droit de 90 °, en divisant le triangle en deux triangles plus petits et égaux. -
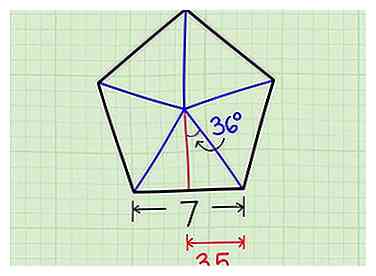 4 Étiquetez l'un des plus petits triangles. Nous pouvons déjà étiqueter un côté et un angle du petit triangle:
4 Étiquetez l'un des plus petits triangles. Nous pouvons déjà étiqueter un côté et un angle du petit triangle: - le base du triangle est ½ du côté du pentagone. Dans notre exemple, il s’agit de ½ x 7 = 3,5 unités.
- le angle au centre du pentagone est toujours 36º.[1] (En commençant par un centre complet de 360º, vous pouvez le diviser en 10 de ces plus petits triangles. 360 ÷ 10 = 36, l'angle à un triangle est donc 36º.)
-
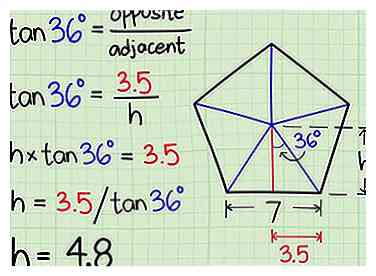 5 Calculez la hauteur du triangle. le la taille de ce triangle est le côté perpendiculaire au bord du pentagone, menant au centre. Nous pouvons utiliser la trigonométrie de début pour trouver la longueur de ce côté:[2]
5 Calculez la hauteur du triangle. le la taille de ce triangle est le côté perpendiculaire au bord du pentagone, menant au centre. Nous pouvons utiliser la trigonométrie de début pour trouver la longueur de ce côté:[2] - Dans un triangle à angle droit, le tangente d'un angle est égal à la longueur du côté opposé, divisé par la longueur du côté adjacent.
- Le côté opposé à l'angle 36º est la base du triangle (la moitié du côté du pentagone). Le côté adjacent à l'angle 36º est la hauteur du triangle.
- bronzage (36º) = opposé / adjacent
- Dans notre exemple, bronzage (36º) = 3.5 / hauteur
- hauteur x tan (36º) = 3.5
- hauteur = 3,5 / tan (36º)
- height = (environ) 4.8 unités.
-
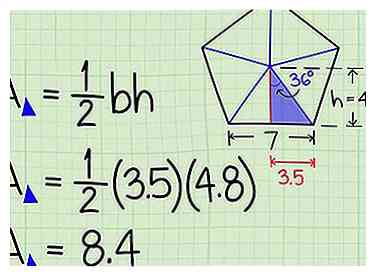 6 Trouve l'aire du triangle. La surface d'un triangle est égale à ½ la base x la hauteur. (A = ½bh.) Maintenant que vous connaissez la hauteur, insérez ces valeurs pour trouver l'aire de votre petit triangle.
6 Trouve l'aire du triangle. La surface d'un triangle est égale à ½ la base x la hauteur. (A = ½bh.) Maintenant que vous connaissez la hauteur, insérez ces valeurs pour trouver l'aire de votre petit triangle. - Dans notre exemple, l'aire du petit triangle = ½bh = ½ (3,5) (4,8) = 8,4 unités carrées.
-
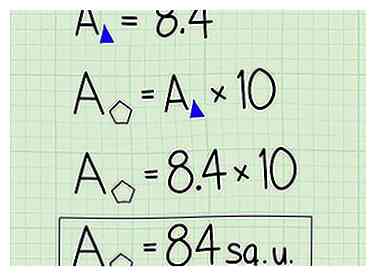 7 Multipliez pour trouver l'aire du pentagone. Un de ces petits triangles couvre 1/10 de la surface du pentagone. Pour trouver la surface totale, multipliez la surface du petit triangle par 10.
7 Multipliez pour trouver l'aire du pentagone. Un de ces petits triangles couvre 1/10 de la surface du pentagone. Pour trouver la surface totale, multipliez la surface du petit triangle par 10. - Dans notre exemple, l'aire de l'ensemble du pentagone = 8.4 x 10 = 84 unités carrées.
Méthode trois sur trois:
Utiliser une formule
-
 1 Utilisez le périmètre et l'apothème. L'apothème est une ligne du centre d'un pentagone qui frappe un côté à angle droit. Si on vous donne sa longueur, vous pouvez utiliser cette formule facile
1 Utilisez le périmètre et l'apothème. L'apothème est une ligne du centre d'un pentagone qui frappe un côté à angle droit. Si on vous donne sa longueur, vous pouvez utiliser cette formule facile - Zone d'un pentagone régulier = Pennsylvanie/ 2, où p = le périmètre une = l'apothème.[3]
- Si vous ne connaissez pas le périmètre, calculez-le à partir de la longueur du côté: p = 5s, où s est la longueur du côté.
-
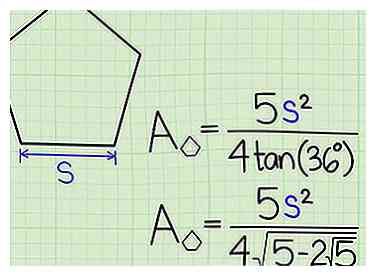 2 Utilisez la longueur du côté. Si vous ne connaissez que la longueur du côté, utilisez la formule suivante:[4]
2 Utilisez la longueur du côté. Si vous ne connaissez que la longueur du côté, utilisez la formule suivante:[4] - Surface d'un pentagone régulier = (5s2) / (4tan (36º)), où s = longueur du côté.
- bronzage (36º) = √ (5-2√5).[5] Donc, si votre calculatrice n’a pas de fonction "tan", utilisez la formule Area = (5s2) / (4√(5-2√5)).
-
 3 Choisissez une formule qui utilise uniquement le rayon. Vous pouvez même trouver la zone si vous ne connaissez que le rayon. Utilisez cette formule:[6]
3 Choisissez une formule qui utilise uniquement le rayon. Vous pouvez même trouver la zone si vous ne connaissez que le rayon. Utilisez cette formule:[6] - Aire d'un pentagone régulier = (5/2)r2le péché (72º), où r est le rayon.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Commencez par la longueur du côté et l'apothème. Cette méthode fonctionne pour les pentagones réguliers, avec cinq côtés égaux. Outre la longueur du côté, vous aurez besoin du "apothème" du pentagone. L'apothème est la ligne allant du centre du pentagone à un côté, coupant le côté à 90 ° à angle droit.
1 Commencez par la longueur du côté et l'apothème. Cette méthode fonctionne pour les pentagones réguliers, avec cinq côtés égaux. Outre la longueur du côté, vous aurez besoin du "apothème" du pentagone. L'apothème est la ligne allant du centre du pentagone à un côté, coupant le côté à 90 ° à angle droit.  2 Divisez le pentagone en cinq triangles. Tracez cinq lignes à partir du centre du pentagone, menant à chaque sommet (coin). Vous avez maintenant cinq triangles.
2 Divisez le pentagone en cinq triangles. Tracez cinq lignes à partir du centre du pentagone, menant à chaque sommet (coin). Vous avez maintenant cinq triangles.  3 Calculez l'aire d'un triangle. Chaque triangle a un base égal au côté du pentagone. Il a aussi un la taille égal à l'apothème du pentagone. (Rappelez-vous que la hauteur d'un triangle va d'un sommet à l'autre, à angle droit.) Pour déterminer l'aire d'un triangle, calculez simplement ½ x base x hauteur.
3 Calculez l'aire d'un triangle. Chaque triangle a un base égal au côté du pentagone. Il a aussi un la taille égal à l'apothème du pentagone. (Rappelez-vous que la hauteur d'un triangle va d'un sommet à l'autre, à angle droit.) Pour déterminer l'aire d'un triangle, calculez simplement ½ x base x hauteur.  4 Multipliez par cinq pour trouver la superficie totale. Nous avons divisé le pentagone en cinq triangles égaux. Pour trouver la surface totale, multipliez simplement l'aire d'un triangle par cinq.
4 Multipliez par cinq pour trouver la superficie totale. Nous avons divisé le pentagone en cinq triangles égaux. Pour trouver la surface totale, multipliez simplement l'aire d'un triangle par cinq.  1 Commencez avec juste la longueur du côté. Cette méthode ne fonctionne que pour les pentagones ordinaires, qui ont cinq côtés de même longueur.
1 Commencez avec juste la longueur du côté. Cette méthode ne fonctionne que pour les pentagones ordinaires, qui ont cinq côtés de même longueur.  2 Divisez le pentagone en cinq triangles. Tracez une ligne du centre du pentagone à n'importe quel sommet. Répétez cette opération pour chaque sommet. Vous avez maintenant cinq triangles, chacun de la même taille.
2 Divisez le pentagone en cinq triangles. Tracez une ligne du centre du pentagone à n'importe quel sommet. Répétez cette opération pour chaque sommet. Vous avez maintenant cinq triangles, chacun de la même taille.  3 Diviser un triangle en deux. Tracez une ligne du centre du pentagone à la base d'un triangle. Cette ligne devrait frapper la base à un angle droit de 90 °, en divisant le triangle en deux triangles plus petits et égaux.
3 Diviser un triangle en deux. Tracez une ligne du centre du pentagone à la base d'un triangle. Cette ligne devrait frapper la base à un angle droit de 90 °, en divisant le triangle en deux triangles plus petits et égaux.  4 Étiquetez l'un des plus petits triangles. Nous pouvons déjà étiqueter un côté et un angle du petit triangle:
4 Étiquetez l'un des plus petits triangles. Nous pouvons déjà étiqueter un côté et un angle du petit triangle:  5 Calculez la hauteur du triangle. le la taille de ce triangle est le côté perpendiculaire au bord du pentagone, menant au centre. Nous pouvons utiliser la trigonométrie de début pour trouver la longueur de ce côté:[2]
5 Calculez la hauteur du triangle. le la taille de ce triangle est le côté perpendiculaire au bord du pentagone, menant au centre. Nous pouvons utiliser la trigonométrie de début pour trouver la longueur de ce côté:[2] 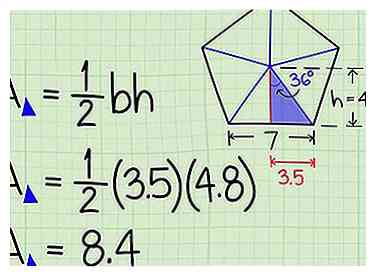 6 Trouve l'aire du triangle. La surface d'un triangle est égale à ½ la base x la hauteur. (A = ½bh.) Maintenant que vous connaissez la hauteur, insérez ces valeurs pour trouver l'aire de votre petit triangle.
6 Trouve l'aire du triangle. La surface d'un triangle est égale à ½ la base x la hauteur. (A = ½bh.) Maintenant que vous connaissez la hauteur, insérez ces valeurs pour trouver l'aire de votre petit triangle. 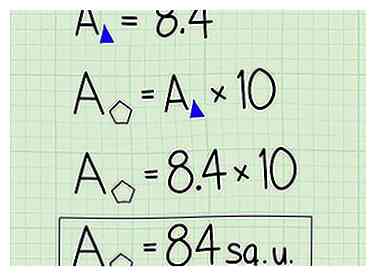 7 Multipliez pour trouver l'aire du pentagone. Un de ces petits triangles couvre 1/10 de la surface du pentagone. Pour trouver la surface totale, multipliez la surface du petit triangle par 10.
7 Multipliez pour trouver l'aire du pentagone. Un de ces petits triangles couvre 1/10 de la surface du pentagone. Pour trouver la surface totale, multipliez la surface du petit triangle par 10.  1 Utilisez le périmètre et l'apothème. L'apothème est une ligne du centre d'un pentagone qui frappe un côté à angle droit. Si on vous donne sa longueur, vous pouvez utiliser cette formule facile
1 Utilisez le périmètre et l'apothème. L'apothème est une ligne du centre d'un pentagone qui frappe un côté à angle droit. Si on vous donne sa longueur, vous pouvez utiliser cette formule facile  2 Utilisez la longueur du côté. Si vous ne connaissez que la longueur du côté, utilisez la formule suivante:[4]
2 Utilisez la longueur du côté. Si vous ne connaissez que la longueur du côté, utilisez la formule suivante:[4]  3 Choisissez une formule qui utilise uniquement le rayon. Vous pouvez même trouver la zone si vous ne connaissez que le rayon. Utilisez cette formule:[6]
3 Choisissez une formule qui utilise uniquement le rayon. Vous pouvez même trouver la zone si vous ne connaissez que le rayon. Utilisez cette formule:[6]