Il existe de nombreuses manières de trouver une dimension manquante d'un rectangle, et la méthode que vous utiliserez dépendra des informations que vous possédez déjà. Tant que vous connaissez la zone ou le périmètre, ainsi que la longueur d'un côté du rectangle (ou la relation entre la longueur et la largeur), vous pouvez trouver une cote manquante. Les propriétés d'un rectangle sont telles que vous pouvez utiliser ces méthodes pour trouver la largeur ou la longueur.
Méthode One of Four:
Utiliser la surface et la longueur
-
 1 Configurez la formule pour l'aire d'un rectangle. La formule est , où est égal à l'aire du rectangle, est égal à la longueur du rectangle et est égal à la largeur du rectangle.[1]
1 Configurez la formule pour l'aire d'un rectangle. La formule est , où est égal à l'aire du rectangle, est égal à la longueur du rectangle et est égal à la largeur du rectangle.[1] - Cette méthode ne fonctionnera que si vous avez la zone et la longueur du rectangle.
- Vous pourriez également voir la formule écrite comme , où est égal à la hauteur du rectangle et est utilisé à la place de la longueur.[2] Ces deux termes font référence à la même mesure.
-
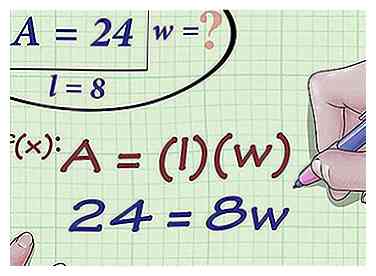 2 Branchez les valeurs de surface et de longueur dans la formule. Assurez-vous de remplacer les variables correctes.
2 Branchez les valeurs de surface et de longueur dans la formule. Assurez-vous de remplacer les variables correctes. - Par exemple, si vous essayez de trouver la largeur d'un rectangle qui a une surface de 24 centimètres carrés et une longueur de 8 centimètres, votre formule ressemblera à ceci:
- Par exemple, si vous essayez de trouver la largeur d'un rectangle qui a une surface de 24 centimètres carrés et une longueur de 8 centimètres, votre formule ressemblera à ceci:
-
 3 Résoudre pour . Pour ce faire, vous devez diviser chaque côté de l'équation par la longueur.
3 Résoudre pour . Pour ce faire, vous devez diviser chaque côté de l'équation par la longueur. - Par exemple, dans l'équation , vous divisez chaque côté par 8.
- Par exemple, dans l'équation , vous divisez chaque côté par 8.
-
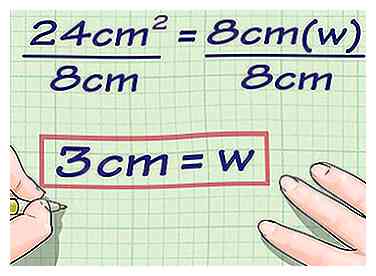 4 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure.
4 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure. - Par exemple, pour un rectangle avec une zone de et une longueur de , la largeur serait .
Méthode deux sur quatre:
Utilisation du périmètre et de la longueur
-
 1 Configurez la formule pour le périmètre d'un rectangle. La formule est , où est égal au périmètre du rectangle, est égal à la longueur du rectangle et est égal à la largeur du rectangle.[3]
1 Configurez la formule pour le périmètre d'un rectangle. La formule est , où est égal au périmètre du rectangle, est égal à la longueur du rectangle et est égal à la largeur du rectangle.[3] - Cette méthode ne fonctionnera que si on vous donne le périmètre et la longueur du rectangle.
- Vous pourriez également voir la formule écrite comme , où est égal à la hauteur du rectangle et est utilisé à la place de la longueur.[4] Les variables et se référer à la même mesure, et la propriété distributive dicte que ces deux formules, bien que disposées différemment, vous donneront le même résultat.
-
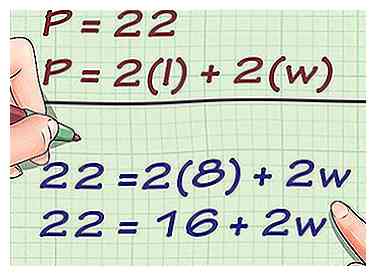 2 Branchez les valeurs du périmètre et de la longueur dans la formule. Assurez-vous de remplacer les variables correctes.
2 Branchez les valeurs du périmètre et de la longueur dans la formule. Assurez-vous de remplacer les variables correctes. - Par exemple, si vous essayez de trouver la largeur d'un rectangle qui a un périmètre de 22 centimètres et une longueur de 8 centimètres, votre formule ressemblera à ceci:
- Par exemple, si vous essayez de trouver la largeur d'un rectangle qui a un périmètre de 22 centimètres et une longueur de 8 centimètres, votre formule ressemblera à ceci:
-
 3 Résoudre pour . Pour ce faire, vous devez soustraire la longueur de chaque côté de l’équation, puis diviser par 2.
3 Résoudre pour . Pour ce faire, vous devez soustraire la longueur de chaque côté de l’équation, puis diviser par 2. - Par exemple, dans l'équation , vous devez soustraire 16 de chaque côté, puis diviser par 2.
- Par exemple, dans l'équation , vous devez soustraire 16 de chaque côté, puis diviser par 2.
-
 4 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure.
4 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure. - Par exemple, pour un rectangle avec un périmètre de et une longueur de , la largeur serait .
Méthode trois sur quatre:
Utiliser la diagonale et la longueur
-
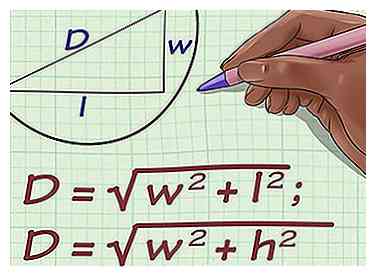 1 Configurez la formule pour la diagonale d'un rectangle. La formule est , où est égal à la longueur de la diagonale du rectangle, est égal à la longueur du rectangle et est égal à la largeur du rectangle.[5]
1 Configurez la formule pour la diagonale d'un rectangle. La formule est , où est égal à la longueur de la diagonale du rectangle, est égal à la longueur du rectangle et est égal à la largeur du rectangle.[5] - Cette méthode ne fonctionnera que si vous avez la longueur de la diagonale et la longueur du côté du rectangle.
- Vous pourriez également voir la formule écrite comme , où est égal à la hauteur du rectangle et est utilisé à la place de la longueur.[6] Les variables et se référer à la même mesure.
-
 2 Branchez les valeurs de la longueur diagonale et latérale dans la formule. Assurez-vous de remplacer les variables correctes.
2 Branchez les valeurs de la longueur diagonale et latérale dans la formule. Assurez-vous de remplacer les variables correctes. - Par exemple, si vous essayez de trouver la largeur d'un rectangle de 5 centimètres de longueur et d'une longueur de 4 centimètres, votre formule ressemblera à ceci:
-
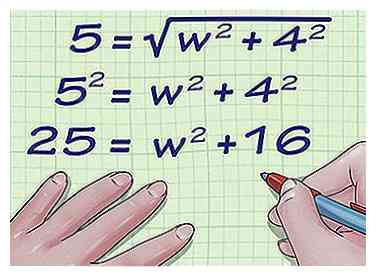 3 Carré des deux côtés de la formule. Vous devez le faire pour vous débarrasser du signe de la racine carrée, ce qui facilite l’isolation de la variable de largeur.
3 Carré des deux côtés de la formule. Vous devez le faire pour vous débarrasser du signe de la racine carrée, ce qui facilite l’isolation de la variable de largeur. - Par exemple:
- Par exemple:
-
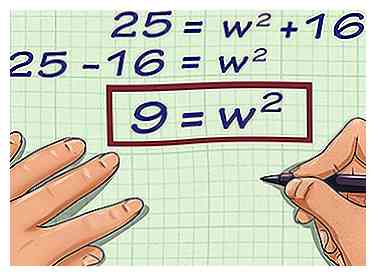 4 Isoler le variable. Pour ce faire, vous devez soustraire la longueur au carré de chaque côté de l'équation.
4 Isoler le variable. Pour ce faire, vous devez soustraire la longueur au carré de chaque côté de l'équation. - Par exemple, dans l'équation , vous soustrayez 16 de chaque côté.
- Par exemple, dans l'équation , vous soustrayez 16 de chaque côté.
-
 5 Résoudre pour . Pour ce faire, vous devez trouver la racine carrée de chaque côté de l'équation.
5 Résoudre pour . Pour ce faire, vous devez trouver la racine carrée de chaque côté de l'équation. - Par exemple:
- Par exemple:
-
 6 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure.
6 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure. - Par exemple, pour un rectangle de longueur diagonale et une longueur de côté de , la largeur serait .
Méthode quatre sur quatre:
Utilisation de la surface ou du périmètre et de la longueur relative
-
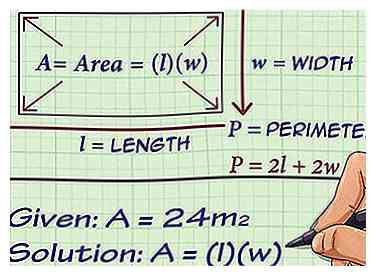 1 Configurez la formule pour l'aire ou le périmètre d'un rectangle. La formule que vous utiliserez dépendra de la mesure qui vous est donnée. Si vous recevez la zone, configurez la formule de zone. Si vous recevez le périmètre, configurez la formule de périmètre.
1 Configurez la formule pour l'aire ou le périmètre d'un rectangle. La formule que vous utiliserez dépendra de la mesure qui vous est donnée. Si vous recevez la zone, configurez la formule de zone. Si vous recevez le périmètre, configurez la formule de périmètre. - Si vous ne connaissez pas la zone ou le périmètre, ou la relation entre la longueur et la largeur, vous ne pouvez pas utiliser cette méthode.
- La formule pour l'aire est .
- La formule pour le périmètre est .
- Par exemple, vous savez peut-être que la surface d'un rectangle est de 24 centimètres carrés, vous devez donc définir la formule pour l'aire d'un rectangle.
-
 2 Écrivez l'expression qui décrit la relation entre la longueur et la largeur. Ecrivez votre expression en termes de quoi équivaut à.
2 Écrivez l'expression qui décrit la relation entre la longueur et la largeur. Ecrivez votre expression en termes de quoi équivaut à. - La relation peut être donnée en indiquant combien de fois un côté est plus grand que l'autre, ou combien d'unités il est plus ou moins.
- Par exemple, vous pouvez savoir que la longueur est cinq centimètres plus longue que la largeur. Votre expression pour la longueur est alors .
-
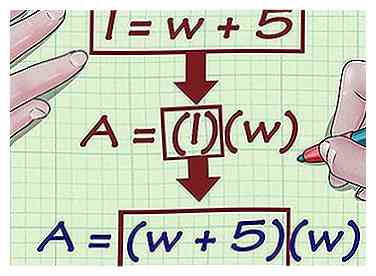 3 Remplace le variable dans votre formule de zone (ou périmètre) avec l'expression de longueur. Votre formule ne devrait maintenant contenir que la variable , ce qui signifie que vous pouvez résoudre pour la largeur.
3 Remplace le variable dans votre formule de zone (ou périmètre) avec l'expression de longueur. Votre formule ne devrait maintenant contenir que la variable , ce qui signifie que vous pouvez résoudre pour la largeur. - Par exemple, si vous savez que cette zone mesure 24 centimètres carrés, et que , votre formule ressemblera à ceci:
- Par exemple, si vous savez que cette zone mesure 24 centimètres carrés, et que , votre formule ressemblera à ceci:
-
 4 Simplifier l'équation. Votre équation simplifiée peut prendre différentes formes, selon la relation entre la longueur et la largeur et selon que vous travaillez avec une zone ou un périmètre.[7] Pensez à mettre en place une équation vous permettant de résoudre de la manière la plus simple.
4 Simplifier l'équation. Votre équation simplifiée peut prendre différentes formes, selon la relation entre la longueur et la largeur et selon que vous travaillez avec une zone ou un périmètre.[7] Pensez à mettre en place une équation vous permettant de résoudre de la manière la plus simple. - Par exemple, vous pouvez simplifier à .
-
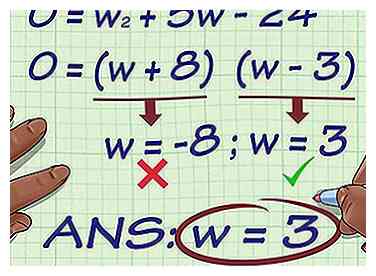 5 Résoudre pour . Encore une fois, comment vous résolvez pour dépendra de votre équation simplifiée. Utilisez les règles de base de l'algèbre et de la géométrie à résoudre.
5 Résoudre pour . Encore une fois, comment vous résolvez pour dépendra de votre équation simplifiée. Utilisez les règles de base de l'algèbre et de la géométrie à résoudre. - Vous devrez peut-être utiliser l'addition ou la division pour résoudre ou vous devrez peut-être prendre en compte une équation quadratique ou utiliser la formule quadratique pour la résoudre.[8]
- Par exemple, peut être factorisé comme suit:
Vous aurez alors deux solutions possibles pour : ou . Comme un rectangle ne peut pas avoir une largeur négative, vous pouvez éliminer -8. Donc, votre solution est .[9]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Configurez la formule pour l'aire d'un rectangle. La formule est
1 Configurez la formule pour l'aire d'un rectangle. La formule est 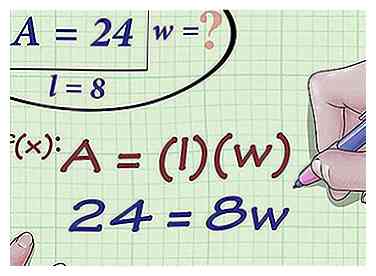 2 Branchez les valeurs de surface et de longueur dans la formule. Assurez-vous de remplacer les variables correctes.
2 Branchez les valeurs de surface et de longueur dans la formule. Assurez-vous de remplacer les variables correctes.  3 Résoudre pour
3 Résoudre pour  4 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure.
4 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure.  1 Configurez la formule pour le périmètre d'un rectangle. La formule est
1 Configurez la formule pour le périmètre d'un rectangle. La formule est 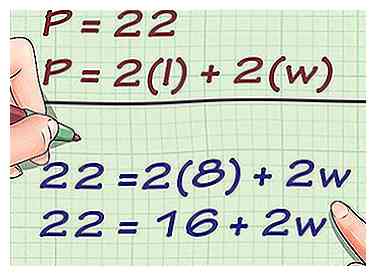 2 Branchez les valeurs du périmètre et de la longueur dans la formule. Assurez-vous de remplacer les variables correctes.
2 Branchez les valeurs du périmètre et de la longueur dans la formule. Assurez-vous de remplacer les variables correctes.  3 Résoudre pour
3 Résoudre pour  4 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure.
4 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure. 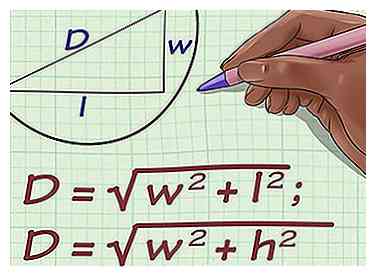 1 Configurez la formule pour la diagonale d'un rectangle. La formule est
1 Configurez la formule pour la diagonale d'un rectangle. La formule est  2 Branchez les valeurs de la longueur diagonale et latérale dans la formule. Assurez-vous de remplacer les variables correctes.
2 Branchez les valeurs de la longueur diagonale et latérale dans la formule. Assurez-vous de remplacer les variables correctes. 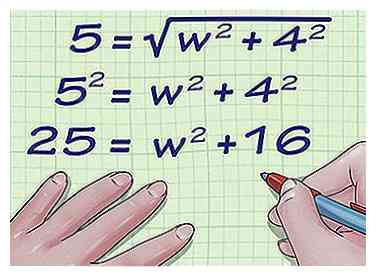 3 Carré des deux côtés de la formule. Vous devez le faire pour vous débarrasser du signe de la racine carrée, ce qui facilite l’isolation de la variable de largeur.
3 Carré des deux côtés de la formule. Vous devez le faire pour vous débarrasser du signe de la racine carrée, ce qui facilite l’isolation de la variable de largeur. 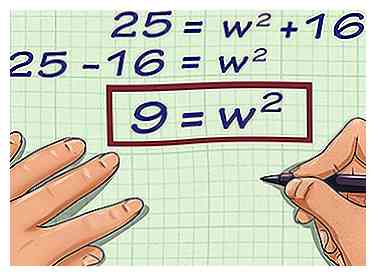 4 Isoler le
4 Isoler le  5 Résoudre pour
5 Résoudre pour  6 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure.
6 Écrivez votre réponse finale. N'oubliez pas d'inclure l'unité de mesure.  1 Configurez la formule pour l'aire ou le périmètre d'un rectangle. La formule que vous utiliserez dépendra de la mesure qui vous est donnée. Si vous recevez la zone, configurez la formule de zone. Si vous recevez le périmètre, configurez la formule de périmètre.
1 Configurez la formule pour l'aire ou le périmètre d'un rectangle. La formule que vous utiliserez dépendra de la mesure qui vous est donnée. Si vous recevez la zone, configurez la formule de zone. Si vous recevez le périmètre, configurez la formule de périmètre.  2 Écrivez l'expression qui décrit la relation entre la longueur et la largeur. Ecrivez votre expression en termes de quoi
2 Écrivez l'expression qui décrit la relation entre la longueur et la largeur. Ecrivez votre expression en termes de quoi 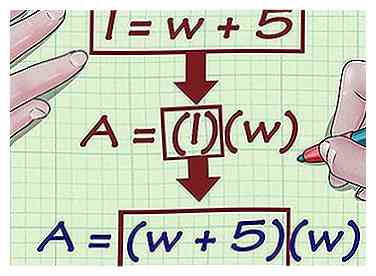 3 Remplace le
3 Remplace le  4 Simplifier l'équation. Votre équation simplifiée peut prendre différentes formes, selon la relation entre la longueur et la largeur et selon que vous travaillez avec une zone ou un périmètre.[7] Pensez à mettre en place une équation vous permettant de résoudre
4 Simplifier l'équation. Votre équation simplifiée peut prendre différentes formes, selon la relation entre la longueur et la largeur et selon que vous travaillez avec une zone ou un périmètre.[7] Pensez à mettre en place une équation vous permettant de résoudre 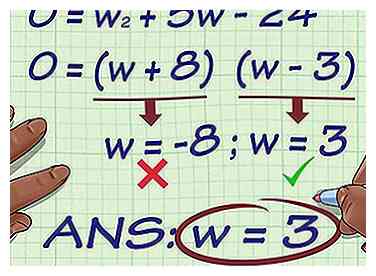 5 Résoudre pour
5 Résoudre pour