Un prisme est une forme tridimensionnelle avec deux bases congruentes parallèles.[1] Dans un prisme triangulaire, les bases sont des triangles. Un prisme triangulaire a également trois côtés latéraux. Pour trouver la surface du prisme triangulaire, vous devez d'abord trouver l'aire des côtés latéraux, puis vous devez trouver l'aire des bases. Enfin, vous devez ajouter ces deux zones pour trouver la surface totale. Ces étapes sont représentées par la formule , où est égal à la zone latérale du prisme et est égal à l'aire d'une base.
Première partie de trois:
Trouver la zone latérale
-
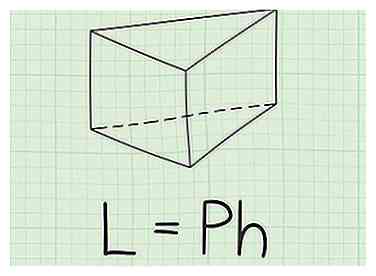 1 Notez la formule pour trouver la zone latérale d'un prisme triangulaire. La formule est , où est égal à la zone latérale du prisme, est égal au périmètre d'une base, et est égal à la hauteur du prisme.[2]
1 Notez la formule pour trouver la zone latérale d'un prisme triangulaire. La formule est , où est égal à la zone latérale du prisme, est égal au périmètre d'une base, et est égal à la hauteur du prisme.[2] - La zone latérale d'un prisme est la surface de tous les côtés ou faces qui ne sont pas la base.[3]
-
 2 Calculez le périmètre d'une base. La base est un triangle, donc il y aura trois côtés. La zone du périmètre d'un triangle est , où , , et sont la longueur de chaque côté du triangle.[4] Peu importe quelle base vous utilisez pour calculer, car les deux bases d'un prisme sont congruentes.[5]
2 Calculez le périmètre d'une base. La base est un triangle, donc il y aura trois côtés. La zone du périmètre d'un triangle est , où , , et sont la longueur de chaque côté du triangle.[4] Peu importe quelle base vous utilisez pour calculer, car les deux bases d'un prisme sont congruentes.[5] - Par exemple, si la base a trois côtés de 6 cm, 5 cm et 4 cm, pour calculer le périmètre, vous additionnez les trois côtés: . Ainsi, le périmètre d'une base est de 15 cm.
-
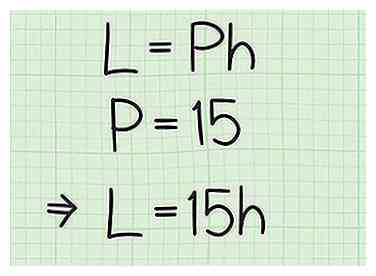 3 Branchez le périmètre dans la formule de la zone latérale. Assurez-vous de remplacer la variable dans la formule.
3 Branchez le périmètre dans la formule de la zone latérale. Assurez-vous de remplacer la variable dans la formule. - Par exemple, .
-
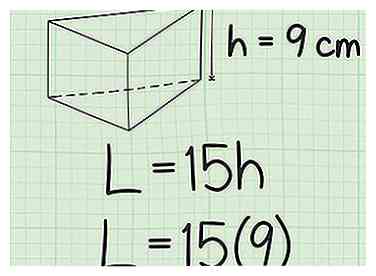 4 Branchez la hauteur du prisme dans la formule de la zone latérale. La hauteur du prisme est la même que la longueur du côté de toute face latérale non reliée à la base. Habituellement (mais pas toujours) ce sera le côté le plus long de la face latérale.
4 Branchez la hauteur du prisme dans la formule de la zone latérale. La hauteur du prisme est la même que la longueur du côté de toute face latérale non reliée à la base. Habituellement (mais pas toujours) ce sera le côté le plus long de la face latérale. - Par exemple, si la hauteur du prisme est de 9 cm, votre formule ressemblera à ceci: .
-
 5 Multipliez le périmètre d'une base avec la hauteur du prisme. Le résultat vous donnera, en unités carrées, la surface latérale du prisme. Il s'agit de la première valeur dont vous avez besoin pour trouver la surface totale du prisme. Vous devez donc définir cette valeur lorsque vous calculez l'aire de la base.
5 Multipliez le périmètre d'une base avec la hauteur du prisme. Le résultat vous donnera, en unités carrées, la surface latérale du prisme. Il s'agit de la première valeur dont vous avez besoin pour trouver la surface totale du prisme. Vous devez donc définir cette valeur lorsque vous calculez l'aire de la base. - Par exemple, Ainsi, la surface latérale du prisme est de 135 centimètres carrés.
Deuxième partie de trois:
Trouver la zone de la base
-
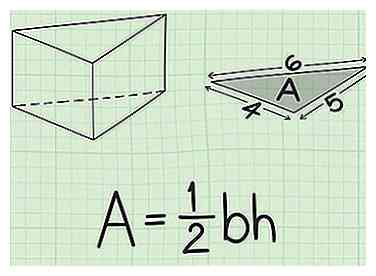 1 Configurez la formule pour l'aire d'un triangle. Comme les bases d'un prisme triangulaire sont des triangles, vous utiliserez cette formule pour calculer leur surface. La formule pour l'aire d'un triangle est , où est égal à l'aire du triangle, est égal à la base du triangle, et est égal à la hauteur du triangle.[6]
1 Configurez la formule pour l'aire d'un triangle. Comme les bases d'un prisme triangulaire sont des triangles, vous utiliserez cette formule pour calculer leur surface. La formule pour l'aire d'un triangle est , où est égal à l'aire du triangle, est égal à la base du triangle, et est égal à la hauteur du triangle.[6] - C'est le moyen le plus courant de calculer l'aire d'un triangle. Si vous ne connaissez pas la hauteur du triangle, vous pouvez également calculer la surface en utilisant la longueur des trois côtés du triangle.
- Il suffit de trouver l'aire d'une base, car les deux bases d'un prisme sont congruentes et auront donc la même surface.[7]
-
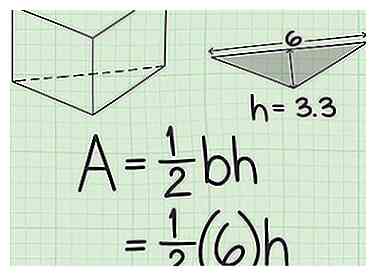 2 Branchez la base du triangle dans la formule. Ne confondez pas la base avec un autre côté du triangle. La base est le côté perpendiculaire à la hauteur.
2 Branchez la base du triangle dans la formule. Ne confondez pas la base avec un autre côté du triangle. La base est le côté perpendiculaire à la hauteur. - Par exemple, si la base du triangle est de 6 cm, votre formule ressemblera à ceci: .
-
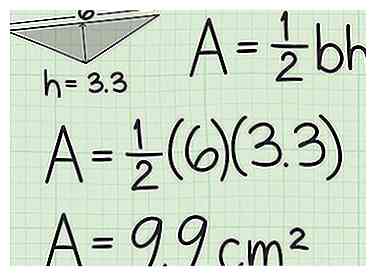 3 Branchez la hauteur du triangle dans la formule. Multipliez la base par la hauteur. Ensuite, prenez la moitié de cette valeur. Cela vous donnera la zone de la base, en unités carrées. Ceci est la deuxième valeur dont vous avez besoin pour calculer la surface totale du prisme.
3 Branchez la hauteur du triangle dans la formule. Multipliez la base par la hauteur. Ensuite, prenez la moitié de cette valeur. Cela vous donnera la zone de la base, en unités carrées. Ceci est la deuxième valeur dont vous avez besoin pour calculer la surface totale du prisme. - Par exemple, si la hauteur est de 3,3 cm, vos calculs ressembleront à ceci:
La surface de la base est donc de 9,9 centimètres carrés.
- Par exemple, si la hauteur est de 3,3 cm, vos calculs ressembleront à ceci:
Troisième partie de trois:
Trouver la surface
-
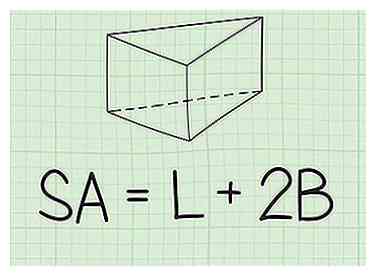 1 Configurez la formule pour trouver la surface d'un prisme. La formule est , où est égal à la surface du prisme, est égal à la zone latérale du prisme, et est égal à l'aire d'une base.[8]
1 Configurez la formule pour trouver la surface d'un prisme. La formule est , où est égal à la surface du prisme, est égal à la zone latérale du prisme, et est égal à l'aire d'une base.[8] -
 2 Branchez la zone latérale dans la formule. C'est la surface de tous les côtés du prisme qui ne sont pas la base. Vous devriez avoir calculé cela précédemment. Assurez-vous de substituer la zone latérale à la variable .
2 Branchez la zone latérale dans la formule. C'est la surface de tous les côtés du prisme qui ne sont pas la base. Vous devriez avoir calculé cela précédemment. Assurez-vous de substituer la zone latérale à la variable . - Par exemple, si la zone latérale de votre prisme triangulaire est de 135 centimètres carrés, votre formule ressemblera à ceci: .
-
 3 Branchez la zone d'une base dans la formule. Assurez-vous d'utiliser la zone d'une seule base, et non la surface totale des deux bases combinées. Remplacer la zone de base pour la variable .
3 Branchez la zone d'une base dans la formule. Assurez-vous d'utiliser la zone d'une seule base, et non la surface totale des deux bases combinées. Remplacer la zone de base pour la variable . - Par exemple, si l'aire d'une base de votre prisme est de 9,9 centimètres carrés, votre formule ressemblera à ceci: .
-
 4 Complétez les calculs. Multipliez la surface de la base par 2, puis ajoutez la zone latérale. Cela vous donnera la surface totale, en unités carrées, de votre prisme triangulaire.
4 Complétez les calculs. Multipliez la surface de la base par 2, puis ajoutez la zone latérale. Cela vous donnera la surface totale, en unités carrées, de votre prisme triangulaire. - Par exemple:
Ainsi, la surface d'un prisme triangulaire avec une base ayant des côtés mesurant 6, 5 et 4 centimètres de longueur et une hauteur de 9 centimètres de longueur a une surface de 154,8 centimètres carrés.
- Par exemple:
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Notez la formule pour trouver la zone latérale d'un prisme triangulaire. La formule est
1 Notez la formule pour trouver la zone latérale d'un prisme triangulaire. La formule est  2 Calculez le périmètre d'une base. La base est un triangle, donc il y aura trois côtés. La zone du périmètre d'un triangle est
2 Calculez le périmètre d'une base. La base est un triangle, donc il y aura trois côtés. La zone du périmètre d'un triangle est  3 Branchez le périmètre dans la formule de la zone latérale. Assurez-vous de remplacer la variable
3 Branchez le périmètre dans la formule de la zone latérale. Assurez-vous de remplacer la variable  4 Branchez la hauteur du prisme dans la formule de la zone latérale. La hauteur du prisme est la même que la longueur du côté de toute face latérale non reliée à la base. Habituellement (mais pas toujours) ce sera le côté le plus long de la face latérale.
4 Branchez la hauteur du prisme dans la formule de la zone latérale. La hauteur du prisme est la même que la longueur du côté de toute face latérale non reliée à la base. Habituellement (mais pas toujours) ce sera le côté le plus long de la face latérale.  5 Multipliez le périmètre d'une base avec la hauteur du prisme. Le résultat vous donnera, en unités carrées, la surface latérale du prisme. Il s'agit de la première valeur dont vous avez besoin pour trouver la surface totale du prisme. Vous devez donc définir cette valeur lorsque vous calculez l'aire de la base.
5 Multipliez le périmètre d'une base avec la hauteur du prisme. Le résultat vous donnera, en unités carrées, la surface latérale du prisme. Il s'agit de la première valeur dont vous avez besoin pour trouver la surface totale du prisme. Vous devez donc définir cette valeur lorsque vous calculez l'aire de la base.  1 Configurez la formule pour l'aire d'un triangle. Comme les bases d'un prisme triangulaire sont des triangles, vous utiliserez cette formule pour calculer leur surface. La formule pour l'aire d'un triangle est
1 Configurez la formule pour l'aire d'un triangle. Comme les bases d'un prisme triangulaire sont des triangles, vous utiliserez cette formule pour calculer leur surface. La formule pour l'aire d'un triangle est  2 Branchez la base du triangle dans la formule. Ne confondez pas la base avec un autre côté du triangle. La base est le côté perpendiculaire à la hauteur.
2 Branchez la base du triangle dans la formule. Ne confondez pas la base avec un autre côté du triangle. La base est le côté perpendiculaire à la hauteur. 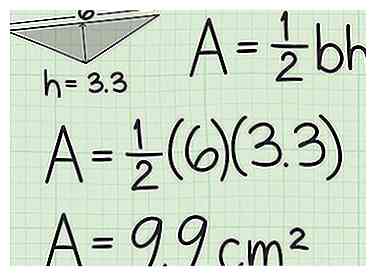 3 Branchez la hauteur du triangle dans la formule. Multipliez la base par la hauteur. Ensuite, prenez la moitié de cette valeur. Cela vous donnera la zone de la base, en unités carrées. Ceci est la deuxième valeur dont vous avez besoin pour calculer la surface totale du prisme.
3 Branchez la hauteur du triangle dans la formule. Multipliez la base par la hauteur. Ensuite, prenez la moitié de cette valeur. Cela vous donnera la zone de la base, en unités carrées. Ceci est la deuxième valeur dont vous avez besoin pour calculer la surface totale du prisme.  1 Configurez la formule pour trouver la surface d'un prisme. La formule est
1 Configurez la formule pour trouver la surface d'un prisme. La formule est  2 Branchez la zone latérale dans la formule. C'est la surface de tous les côtés du prisme qui ne sont pas la base. Vous devriez avoir calculé cela précédemment. Assurez-vous de substituer la zone latérale à la variable
2 Branchez la zone latérale dans la formule. C'est la surface de tous les côtés du prisme qui ne sont pas la base. Vous devriez avoir calculé cela précédemment. Assurez-vous de substituer la zone latérale à la variable  3 Branchez la zone d'une base dans la formule. Assurez-vous d'utiliser la zone d'une seule base, et non la surface totale des deux bases combinées. Remplacer la zone de base pour la variable
3 Branchez la zone d'une base dans la formule. Assurez-vous d'utiliser la zone d'une seule base, et non la surface totale des deux bases combinées. Remplacer la zone de base pour la variable  4 Complétez les calculs. Multipliez la surface de la base par 2, puis ajoutez la zone latérale. Cela vous donnera la surface totale, en unités carrées, de votre prisme triangulaire.
4 Complétez les calculs. Multipliez la surface de la base par 2, puis ajoutez la zone latérale. Cela vous donnera la surface totale, en unités carrées, de votre prisme triangulaire.