Comment trouver l'aire d'un quadrilatère (avec des feuilles de triche)

On vous a donc assigné des devoirs qui vous obligent à trouver l'aire d'un quadrilatère… mais vous ne savez même pas ce qu'est un quadrilatère. Ne vous inquiétez pas, l'aide est là! Un quadrilatère est une forme à quatre côtés - les carrés, les rectangles et les diamants ne sont que quelques exemples. Pour trouver l'aire d'un quadrilatère, il vous suffit d'identifier le type de quadrilatère avec lequel vous travaillez et de suivre une formule simple. C'est tout!

Méthode One of Four:
Carrés, rectangles et autres parallélogrammes

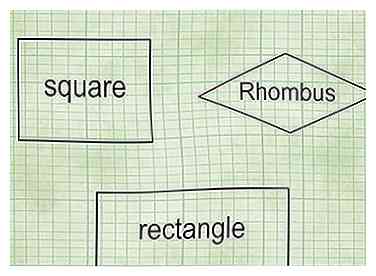1 Savoir identifier un parallélogramme. Un parallélogramme est une forme à quatre côtés avec deux paires de côtés parallèles où les côtés opposés ont la même longueur. Les parallélogrammes comprennent:
- Carrés: Quatre côtés, tous de même longueur. Quatre coins, tous à 90 degrés (angles droits).
- Rectangles: Quatre côtés; les côtés opposés ont les mêmes longueurs. Quatre coins, tous à 90 degrés.
- Losanges: Quatre côtés, tous de même longueur. Quatre coins; aucun ne doit être à 90 degrés mais les angles opposés doivent avoir les mêmes angles.
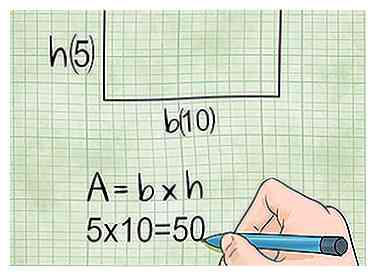2 Multipliez la hauteur des temps de base pour obtenir l'aire d'un rectangle. Pour trouver l'aire d'un rectangle, vous avez besoin de deux mesures: la largeur ou la base (le côté le plus long du rectangle) et la longueur ou la hauteur (le côté le plus court du rectangle). Ensuite, multipliez-les simplement pour obtenir la zone. En d'autres termes:
- Surface = base × hauteur, ou A = b × h pour faire court.
- Exemple: Si la base d'un rectangle a une longueur de 10 pouces et que la hauteur a une longueur de 5 pouces, l'aire du rectangle est simplement 10 × 5 (b × h) = 50 pouces carrés.
- N'oubliez pas que lorsque vous trouvez une zone de forme, vous utiliserez unités carrées (pouces carrés, pieds carrés, mètres carrés, etc.) pour votre réponse.
3 Multipliez un côté par lui-même pour trouver l'aire d'un carré. Les carrés sont essentiellement des rectangles spéciaux, vous pouvez donc utiliser la même formule pour trouver leur zone. Cependant, puisque les côtés d'un carré ont tous la même longueur, vous pouvez utiliser le raccourci de multiplication par la longueur d'un côté. C'est comme multiplier la base du carré par sa hauteur car la base et la hauteur sont toujours les mêmes. Utilisez l'équation suivante:^[1]
- Zone = côté × côté ou A = s²
- Exemple: Si un côté d'un carré a une longueur de 4 pieds (t = 4), l'aire de ce carré est simplement t²ou 4 x 4 = 16 pieds carrés.
4 Multipliez les diagonales et divisez par deux pour trouver l'aire d'un losange. Soyez prudent avec celui-ci - lorsque vous trouvez l'aire d'un losange, vous ne pouvez pas simplement multiplier deux côtés adjacents. Au lieu de cela, trouvez les diagonales (les lignes reliant chaque ensemble de coins opposés), multipliez-les et divisez-les par deux. En d'autres termes: ^[2]
- Area = (Diag. 1 × Diag. 2) / 2 ou A = (d₁ × d₂)/2
- Exemple: Si un losange a des diagonales d'une longueur de 6 mètres et 8 mètres, sa surface est simplement (6 × 8) / 2 = 48/2 = 24 mètres carrés.
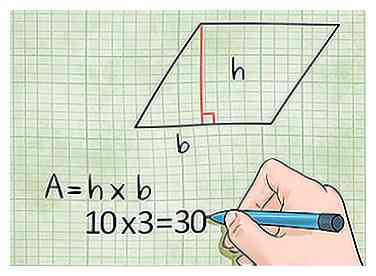5 Sinon, utilisez la base × hauteur pour trouver l'aire d'un losange. Techniquement, vous pouvez également utiliser la formule de hauteur des temps de base pour trouver l'aire d'un losange. Ici, "base" et "height" ne signifient pas que vous pouvez simplement multiplier deux côtés adjacents. Tout d'abord, choisissez un côté comme base. Ensuite, tracez une ligne de la base vers le côté opposé. La ligne doit rencontrer les deux côtés à 90 degrés. La longueur de ce côté est ce que vous devez utiliser pour la hauteur.
- Exemple: Un losange a des côtés de 10 milles et 5 milles. La distance en ligne droite entre les côtés (16,1 km) est de 4,8 km. Si vous voulez trouver la zone du losange, vous devriez multiplier 10 × 3 = 30 miles carrés.
6 Sachez que les formules de losange et de rectangle fonctionnent pour les carrés. La formule côté / côté donnée ci-dessus pour les carrés est de loin la manière la plus pratique de trouver la zone pour ces formes. Cependant, comme les carrés sont techniquement à la fois des rectangles et des losanges ainsi que des carrés, vous pouvez utiliser les formules de surface de ces formes pour les carrés et obtenir la réponse correcte. En d'autres termes, pour les carrés:
- Surface = base × hauteur ou A = b × h
- Area = (Diag. 1 × Diag. 2) / 2 ou A = (d₁ × d₂)/2
- Exemple: Une forme à quatre côtés a deux côtés adjacents avec des longueurs de 4 mètres. Vous pouvez trouver l'aire de ce carré en multipliant sa base par sa hauteur: 4 × 4 = 16 mètres carrés.
- Exemple: Les diagonales d'un carré sont toutes deux égales à 10 centimètres. Vous pouvez trouver l'aire de ce carré avec la formule diagonale: (10 × 10) / 2 = 100/2 = 50 centimètres carrés.

Méthode deux sur quatre:
Trouver l'aire d'un trapèze

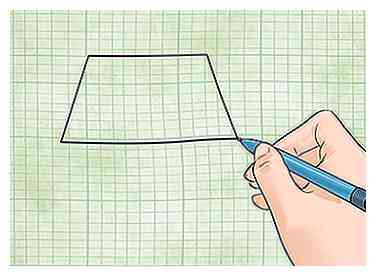1 Savoir identifier un trapèze. Un trapèze est un quadrilatère dont au moins deux côtés sont parallèles. Ses coins peuvent avoir des angles quelconques. Chacun des quatre côtés d’un trapèze peut avoir une longueur différente.
- Vous pouvez trouver l'aire d'un trapèze de deux manières différentes, en fonction des informations dont vous disposez. Ci-dessous, vous verrez comment utiliser les deux.
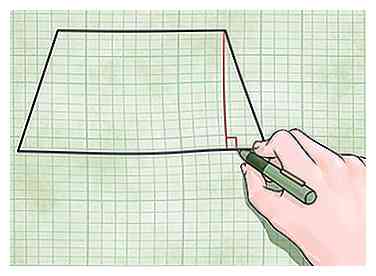2 Trouvez la hauteur du trapèze. La hauteur d'un trapèze est la perpendiculaire reliant les deux côtés parallèles. Cette volonté ne pas ont généralement la même longueur que l'un des côtés, car les côtés sont généralement pointus en diagonale. Vous en aurez besoin pour les deux équations de zone. Voici comment trouver la hauteur d'un trapèze:^[3]
- Trouvez la plus courte des deux lignes de base (les côtés parallèles). Placez votre crayon au coin entre cette ligne de base et l’un des côtés non parallèles.Tracez une ligne droite qui rencontre les deux lignes de base à angle droit. Mesurer cette ligne pour trouver la hauteur.
- Vous pouvez aussi parfois utiliser la trigonométrie pour déterminer la hauteur si la ligne de hauteur, la base et l’autre côté forment un triangle rectangle. Voir notre article trig pour plus d'informations.
3 Trouvez la zone du trapèze en utilisant la hauteur et la longueur des bases. Si vous connaissez la hauteur du trapèze ainsi que la longueur des deux bases, utilisez l'équation suivante:
- Surface = (Base 1 + Base 2) / 2 × Hauteur ou A = (a + b) / 2 × h
- Exemple: Si vous avez un trapèze avec une base de 7 verges, une autre base de 11 verges et que la ligne de hauteur les reliant fait 2 verges, vous pouvez trouver sa zone comme suit: (7 + 11) / 2 × 2 = (18) / 2 × 2 = 9 × 2 = 18 verges.
- Si la hauteur est 10 et que les bases ont des longueurs de 7 et 9, alors vous pouvez trouver la zone simplement en procédant comme suit: (7 + 9) / 2 * 10 = (16/2) * 10 = 8 * 10 = 80
4 Multipliez le midsegment par deux pour trouver l'aire d'un trapèze. Le midsegment est une ligne imaginaire parallèle aux lignes inférieure et supérieure du trapèze et à la même distance. Depuis la mi-parcours est toujours égal à (Base 1 + Base 2) / 2, si vous le connaissez, vous pouvez utiliser un raccourci pour la formule trapézoïdale:
- Surface = Midsegment × Hauteur ou A = m × h
- Essentiellement, cela équivaut à utiliser la formule originale, sauf que vous utilisez "m" au lieu de (a + b) / 2.
- 'Exemple:' Le milieu du trapèze dans l'exemple ci-dessus fait 9 mètres de long. Cela signifie que nous pouvons trouver l'aire du trapèze simplement en multipliant 9 × 2 = 18 verges, juste comme avant.

Méthode trois sur quatre:
Trouver l'aire d'un cerf-volant

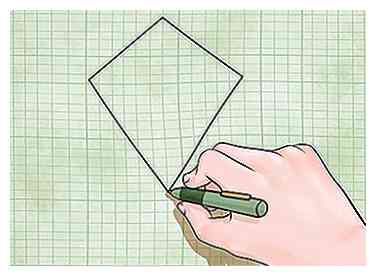1 Savoir identifier un cerf-volant Un cerf-volant est une forme à quatre côtés avec deux paires de côtés de même longueur qui sont adjacent l'un à l'autre, pas l'un en face de l'autre. Comme leur nom l'indique, les cerfs-volants ressemblent à des cerfs-volants réels.
- Il y a deux façons différentes de trouver l'aire d'un cerf-volant en fonction des informations dont vous disposez. Vous trouverez ci-dessous comment utiliser les deux.
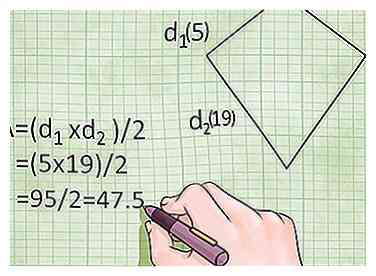2 Utilisez la formule diagonale du losange pour trouver l'aire d'un cerf-volant. Comme un losange est juste un type spécial de cerf-volant où les côtés ont la même longueur, vous pouvez utiliser la formule de la zone en losange en diagonale pour trouver également une zone de cerf-volant. Pour rappel, les diagonales sont les lignes droites entre deux coins opposés du cerf-volant. Comme un losange, la formule de la zone de cerf-volant est la suivante:
- Area = (Diag. 1 × Diag 2.) / 2 ou A = (d₁ × d₂)/2
- Exemple: Si un cerf-volant a des diagonales avec des longueurs de 19 mètres et 5 mètres, sa surface est simplement (19 × 5) / 2 = 95/2 = 47,5 mètres carrés.
- Si vous ne connaissez pas la longueur des diagonales et que vous ne pouvez pas les mesurer, vous pouvez utiliser la trigonométrie pour les calculer. Voir notre article sur la recherche de l'aire d'un cerf-volant pour plus d'informations.
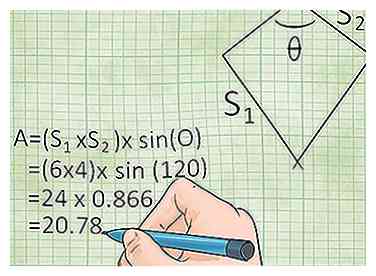3 Utilisez les longueurs des côtés et l'angle entre eux pour trouver la zone. Si vous connaissez les deux valeurs différentes pour les longueurs des côtés et l'angle au coin entre ces côtés, vous pouvez résoudre la zone du cerf-volant avec les principes de la trigonométrie.^[4] Cette méthode nécessite de savoir comment faire des fonctions sinusoïdales (ou au moins d'avoir une calculatrice avec une fonction sinus). Consultez notre article trig pour plus d'informations ou utilisez la formule ci-dessous:
- Area = (Side 1 × Side 2) × sin (angle) ou A = (s)₁ × s₂) × sin (θ) (où θ est l'angle entre les côtés 1 et 2).
- Exemple: Vous avez un cerf-volant avec deux côtés de longueur 6 pieds et deux côtés de longueur 4 pieds. L'angle entre eux est d'environ 120 degrés. Dans ce cas, vous pouvez résoudre le problème comme suit: (6 × 4) × sin (120) = 24 × 0,866 = 20,78 pieds carrés
- Notez que vous devez utiliser les deux différent les côtés et l'angle entre eux ici - l'utilisation de l'ensemble des côtés de même longueur ne fonctionnera pas.

Méthode quatre sur quatre:
Résoudre n'importe quel quadrilatère

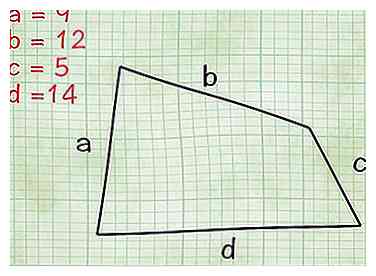1 Trouvez les longueurs des quatre côtés. Votre quadrilatère ne tombe-t-il dans aucune des catégories ci-dessus (par exemple, a-t-il des côtés de longueurs différentes et des ensembles de côtés parallèles nuls?) Croyez-le ou non, il existe des formules quadrilatère, quelle que soit sa forme. Dans cette section, vous trouverez comment utiliser le plus commun. Notez que cette formule nécessite une connaissance de la trigonométrie (encore une fois, voici notre guide trigonométrique de base.
- Tout d'abord, vous devez trouver des longueurs de chacun des quatre côtés du quadrilatère. Aux fins de cet article, nous allons les étiqueter une, b, c et ré. Côtés une et c sont opposés les uns des autres et des côtés b et ré sont en face l'un de l'autre.
- Exemple: Si vous avez un quadrilatère de forme étrange qui ne rentre dans aucune des catégories ci-dessus, mesurez d'abord ses quatre côtés. Disons qu'ils ont des longueurs de 12, 9, 5 et 14 pouces. Dans les étapes ci-dessous, vous utiliserez cette information pour trouver la zone de la forme.
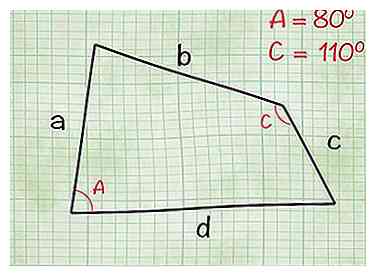2 Trouver les angles entre une et ré et b et c. Lorsque vous travaillez avec un quadrilatère irrégulier, vous ne pouvez pas trouver la zone uniquement sur les côtés. Continuez en trouvant deux des angles opposés. Pour les besoins de cette section, nous utiliserons l’angle UNE entre les côtés une et réet angle C entre les côtés b et c. Cependant, vous pouvez également le faire avec les deux autres angles opposés.
- Exemple: Disons que dans votre quadrilatère, UNE est égal à 80 degrés et C est égal à 110 degrés. À l'étape suivante, vous utiliserez ces valeurs pour trouver la surface totale.
3 Utilisez la formule en triangle pour trouver l'aire du quadrilatère. Imaginez qu'il y ait une ligne droite du coin entre une et b au coin entre c et ré. Cette ligne diviserait le quadrilatère en deux triangles. Puisque l'aire d'un triangle est un BpéchéC, où C est l'angle entre les côtés une et b, vous pouvez utiliser cette formule deux fois (une fois pour chacun de vos triangles imaginaires) pour obtenir l'aire totale du quadrilatère. En d'autres termes, pour tout quadrilatère:
- Zone = 0.5 Côté 1 × Côté 4 × sin (Angle 1 & 4) + 0.5 × Côté 2 × Côté 3 × (Angle 2 & 3) ou
- Aire = 0.5 a × d × sin A + 0.5 × b × c × sin C
- Exemple: Vous avez déjà les côtés et les angles dont vous avez besoin, alors résolvons:
  
  = 0,5 (12 × 14) × sin (80) + 0,5 × (9 × 5) × sin (110)
  
  = 84 × sin (80) + 22,5 × péché (110)
  
  = 84 × 0.984 + 22.5 × 0.939
  
  = 82.66 + 21.13 = 103,79 pouces carrés
- Notez que si vous essayez de trouver l'aire d'un parallélogramme, dans lequel les angles opposés sont égaux, l'équation se réduit à Surface = 0.5 * (ad + bc) * sin A.