Comment trouver l'aire d'un carré en utilisant la longueur de sa diagonale

La formule la plus courante pour l'aire d'un carré est simple: c'est la longueur du côté carré, ou s². Mais parfois, vous ne connaissez que la longueur de la diagonale du carré, entre des sommets opposés. Si vous avez étudié les triangles rectangles, vous pouvez trouver une nouvelle formule de zone qui utilise cette diagonale comme seule variable.

Première partie de deux:
Trouver la zone depuis la diagonale

1. 1 Dessine ton carré. Un carré a quatre côtés égaux. Disons que chacun a une longueur de "s".
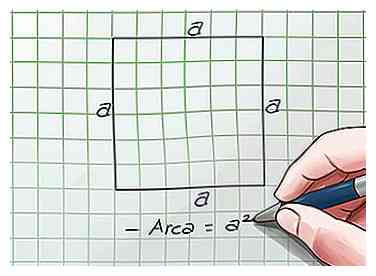2. 2 Passez en revue la formule de base pour une zone carrée. La surface d'un carré est égale à sa longueur multipliée par sa largeur. Puisque chaque côté est s, la formule est Area = s x s = s². Ce sera utile plus tard.
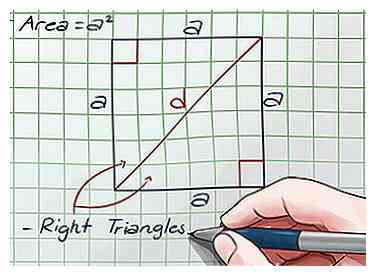3. 3 Rejoignez deux coins opposés pour créer une diagonale. Soit la mesure de cette diagonale être ré unités. Cette diagonale divise le carré en deux triangles droits.
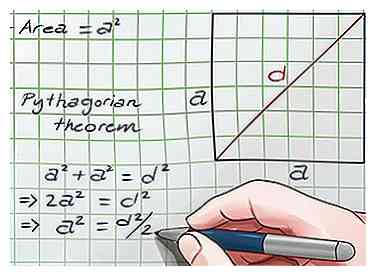4. 4 Appliquez le théorème de Pythagore à l'un des triangles. Le théorème de Pythagore est une formule pour trouver l'hypoténuse (côté le plus long) d'un triangle rectangle: (côté un)² + (côté deux)² = (hypoténuse)², ou $\ displaystyle a ^ 2 + b ^ 2 = c ^ 2$. Maintenant que le carré est divisé en deux, vous pouvez utiliser cette formule sur l'un des triangles de droite:
   • Les deux côtés plus courts du triangle sont les côtés du carré: chacun a une longueur de s.
   • L'hypoténuse est la diagonale du carré, ré.
   • $\ displaystyle s ^ 2 + s ^ 2 = d ^ 2$
5. 5 Organiser l'équation de manière à ce que² est d'un côté. Rappelez-vous que nous savons déjà que l'aire du carré est égale à s². Si vous pouvez obtenir s² Seul sur le côté, vous aurez une nouvelle équation pour la zone:
   • $\ displaystyle s ^ 2 + s ^ 2 = d ^ 2$
   • Simplifier: $\ displaystyle 2s ^ 2 = d ^ 2$
   • Diviser les deux côtés par deux: $\ displaystyle s ^ 2 = \ frac d ^ 2 2$
   • Zone = $\ displaystyle s ^ 2 = \ frac d ^ 2 2$
   • Zone = $\ displaystyle \ frac d ^ 2 2$
6. 6 Utilisez cette formule sur un exemple de carré. Ces étapes ont prouvé que la formule Area = $\ displaystyle \ frac d ^ 2 2$ fonctionne pour tous les carrés. Il suffit de brancher la longueur de la diagonale pour ré et résoudre.
   • Par exemple, disons qu'un carré a une diagonale qui mesure 10 cm.
   • Zone = $\ displaystyle \ frac 10 ^ 2 2$
     = $\ displaystyle \ frac 100 2$
     = 50 centimètres carrés.

Deuxième partie de deux:
Information additionnelle

1. 1 Trouvez la diagonale de la longueur d'un côté. Le théorème de Pythagore pour un carré avec un côté s et diagonale ré vous donne la formule $\ displaystyle 2s ^ 2 = d ^ 2$. Résolvez pour d si vous connaissez les longueurs latérales et souhaitez trouver la longueur de la diagonale:
   • $\ displaystyle 2s ^ 2 = d ^ 2$
     $\ displaystyle \ sqrt 2s ^ 2 = \ sqrt d ^ 2$
     $\ displaystyle s \ sqrt 2 = d$
   • Par exemple, si un carré a des côtés de 7 pouces, sa diagonale d = 7√2 pouces ou environ 9,9 pouces.
   • Si vous n'avez pas de calculatrice, vous pouvez utiliser 1.4 comme estimation pour √2.
2. 2 Trouver la longueur du côté de la diagonale. Si on vous donne la diagonale et que vous savez que la diagonale d'un carré est $\ displaystyle s \ sqrt 2$, vous pouvez diviser les deux côtés par $\ displaystyle \ sqrt 2$ obtenir $\ displaystyle s = \ frac d \ sqrt 2$.
   • Par exemple, un carré de 10 cm de diagonale a des côtés de longueur $\ displaystyle \ frac 10 \ sqrt 2 = 7.071$ cm.
   • Si vous avez besoin de trouver à la fois la longueur du côté et la surface de la diagonale, vous pouvez d’abord utiliser cette formule, puis rapidement la réponse carrée pour obtenir l’aire: $\ displaystyle = s ^ 2 = 7,071 ^ 2 = 50$ centimètres carrés C'est un peu moins précis, car $\ displaystyle \ sqrt 2$ est un nombre irrationnel qui peut entraîner des erreurs d'arrondi.
3. 3 Interpréter la formule de la zone. Le calcul mathématique extrait la formule Area = $\ displaystyle \ frac d ^ 2 2$, mais existe-t-il un moyen de tester cela directement? Bien, $\ displaystyle d ^ 2$ est la surface d'un deuxième carré avec la diagonale comme côté. Puisque la formule complète est $\ showstyle \ frac d ^ 2 2$, vous pouvez penser que ce deuxième carré a exactement deux fois la surface de la place d'origine. Vous pouvez tester cela vous-même:
   • Tracez un carré sur un morceau de papier. Assurez-vous que tous les côtés sont égaux.
   • Mesurer la diagonale. Tracez un deuxième carré en utilisant cette mesure comme la longueur du carré.
   • Tracez une copie de votre premier carré pour en avoir deux. Couper les trois carrés.
   • Découpez les deux petits carrés dans des formes quelconques pour pouvoir les ranger dans le grand carré. Ils doivent remplir parfaitement l’espace, en montrant que la surface du grand carré est exactement le double de celle du petit carré.