Un polygone régulier est une figure convexe à deux dimensions dont les côtés et les angles sont égaux en termes de mesure. De nombreux polygones, tels que les quadrilatères ou les triangles, ont des formules simples pour trouver leurs zones, mais si vous travaillez avec un polygone comportant plus de quatre côtés, vous pouvez utiliser une formule utilisant l'apothème et le périmètre de la forme. Avec un peu d'effort, vous pouvez trouver l'aire des polygones réguliers en quelques minutes.
Première partie de deux:
Calcul de la surface
-
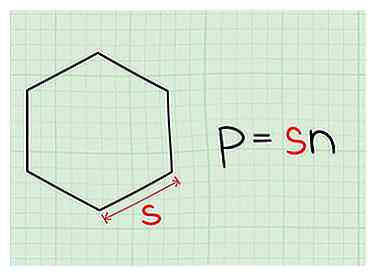 1 Calculez le périmètre. Le périmètre est la longueur combinée du contour de toute figure à deux dimensions. Pour un polygone régulier, il peut être calculé en multipliant la longueur d'un côté par le nombre de côtés (n).[1]
1 Calculez le périmètre. Le périmètre est la longueur combinée du contour de toute figure à deux dimensions. Pour un polygone régulier, il peut être calculé en multipliant la longueur d'un côté par le nombre de côtés (n).[1] -
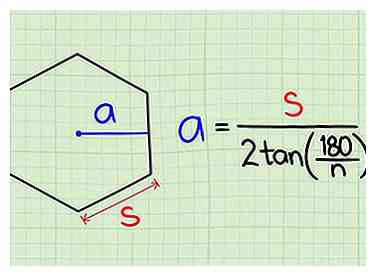 2 Détermine l'apothème. L'apothème d'un polygone régulier est la plus courte distance entre le centre et l'un des côtés, créant un angle droit. C'est un peu plus compliqué à calculer que le périmètre.
2 Détermine l'apothème. L'apothème d'un polygone régulier est la plus courte distance entre le centre et l'un des côtés, créant un angle droit. C'est un peu plus compliqué à calculer que le périmètre. - La formule pour calculer la longueur de l'apothème est la suivante: la longueur du côté (s) divisé par 2 fois la tangente (tan) de 180 degrés divisée par le nombre de côtés (n).
-
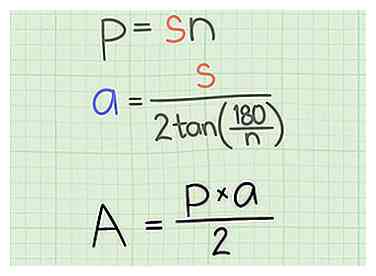 3 Connaître la bonne formule L'aire de tout polygone régulier est donnée par la formule: Zone = (une X p)/2, où une est la longueur de l'apothème et p est le périmètre du polygone.
3 Connaître la bonne formule L'aire de tout polygone régulier est donnée par la formule: Zone = (une X p)/2, où une est la longueur de l'apothème et p est le périmètre du polygone. -
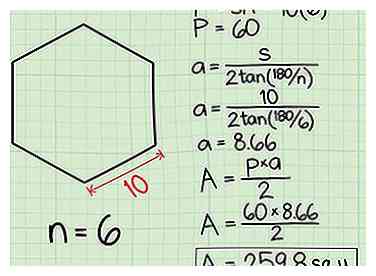 4 Branchez les valeurs de une et p dans la formule et obtenir la zone. Par exemple, utilisons un hexagone (6 côtés) avec un côté (s) longueur de 10.
4 Branchez les valeurs de une et p dans la formule et obtenir la zone. Par exemple, utilisons un hexagone (6 côtés) avec un côté (s) longueur de 10. - Le périmètre est de 6 x 10 (n X s), égal à 60 (donc p = 60).
- L'apothème est calculé par sa propre formule, en branchant 6 et 10 pour n et s. Le résultat de 2tan (180/6) est 1,1547, puis 10 divisé par 1,1547 est égal à 8,66.
- La zone du polygone est Région = une X p / 2, ou 8,66 multiplié par 60 divisé par 2. La solution est une surface de 259,8 unités.
- Notez également qu'il n'y a pas de parenthèse dans l'équation "Area", donc 8,66 divisé par 2 multiplié par 60 vous donnera le même résultat, tout comme 60 divisé par 2 multiplié par 8,66 vous donnera le même résultat.
Deuxième partie de deux:
Comprendre les concepts d'une manière différente
-
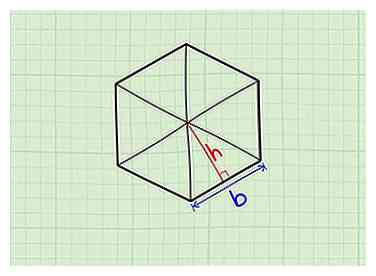 1 Comprendre qu'un polygone régulier peut être considéré comme une collection de triangles. Chaque côté représente la base d'un triangle et il y a autant de triangles dans le polygone que de côtés. Chacun des triangles est égal en longueur, en hauteur et en surface.[2]
1 Comprendre qu'un polygone régulier peut être considéré comme une collection de triangles. Chaque côté représente la base d'un triangle et il y a autant de triangles dans le polygone que de côtés. Chacun des triangles est égal en longueur, en hauteur et en surface.[2] -
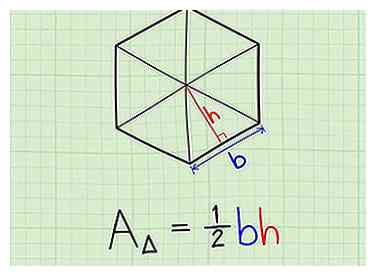 2 Rappelez-vous la formule pour l'aire d'un triangle. L'aire de tout triangle est égale à 1/2 fois la longueur de la base (qui, dans le polygone, est la longueur d'un côté) multipliée par la hauteur (qui est la même que l'apothème en polygone régulier).[3]
2 Rappelez-vous la formule pour l'aire d'un triangle. L'aire de tout triangle est égale à 1/2 fois la longueur de la base (qui, dans le polygone, est la longueur d'un côté) multipliée par la hauteur (qui est la même que l'apothème en polygone régulier).[3] -
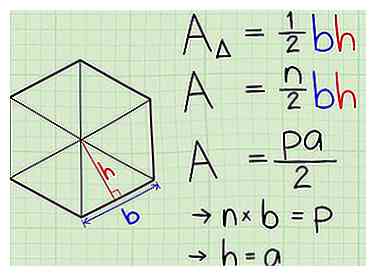 3 Voir les similitudes. Encore une fois, la formule pour un polygone régulier est 1/2 fois plus grande que l'apothème multiplié par le périmètre. Le périmètre est juste la longueur d'un côté multiplié par le nombre de côtés (n); pour un polygone régulier, n représente également le nombre de triangles qui composent la figure. La formule n'est donc rien d'autre que l'aire d'un triangle multipliée par le nombre de triangles du polygone.[4]
3 Voir les similitudes. Encore une fois, la formule pour un polygone régulier est 1/2 fois plus grande que l'apothème multiplié par le périmètre. Le périmètre est juste la longueur d'un côté multiplié par le nombre de côtés (n); pour un polygone régulier, n représente également le nombre de triangles qui composent la figure. La formule n'est donc rien d'autre que l'aire d'un triangle multipliée par le nombre de triangles du polygone.[4]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Calculez le périmètre. Le périmètre est la longueur combinée du contour de toute figure à deux dimensions. Pour un polygone régulier, il peut être calculé en multipliant la longueur d'un côté par le nombre de côtés (n).[1]
1 Calculez le périmètre. Le périmètre est la longueur combinée du contour de toute figure à deux dimensions. Pour un polygone régulier, il peut être calculé en multipliant la longueur d'un côté par le nombre de côtés (n).[1]  2 Détermine l'apothème. L'apothème d'un polygone régulier est la plus courte distance entre le centre et l'un des côtés, créant un angle droit. C'est un peu plus compliqué à calculer que le périmètre.
2 Détermine l'apothème. L'apothème d'un polygone régulier est la plus courte distance entre le centre et l'un des côtés, créant un angle droit. C'est un peu plus compliqué à calculer que le périmètre. 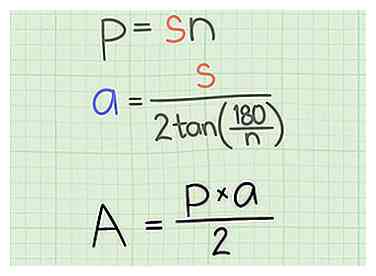 3 Connaître la bonne formule L'aire de tout polygone régulier est donnée par la formule: Zone = (une X p)/2, où une est la longueur de l'apothème et p est le périmètre du polygone.
3 Connaître la bonne formule L'aire de tout polygone régulier est donnée par la formule: Zone = (une X p)/2, où une est la longueur de l'apothème et p est le périmètre du polygone.  4 Branchez les valeurs de une et p dans la formule et obtenir la zone. Par exemple, utilisons un hexagone (6 côtés) avec un côté (s) longueur de 10.
4 Branchez les valeurs de une et p dans la formule et obtenir la zone. Par exemple, utilisons un hexagone (6 côtés) avec un côté (s) longueur de 10.  1 Comprendre qu'un polygone régulier peut être considéré comme une collection de triangles. Chaque côté représente la base d'un triangle et il y a autant de triangles dans le polygone que de côtés. Chacun des triangles est égal en longueur, en hauteur et en surface.[2]
1 Comprendre qu'un polygone régulier peut être considéré comme une collection de triangles. Chaque côté représente la base d'un triangle et il y a autant de triangles dans le polygone que de côtés. Chacun des triangles est égal en longueur, en hauteur et en surface.[2]  2 Rappelez-vous la formule pour l'aire d'un triangle. L'aire de tout triangle est égale à 1/2 fois la longueur de la base (qui, dans le polygone, est la longueur d'un côté) multipliée par la hauteur (qui est la même que l'apothème en polygone régulier).[3]
2 Rappelez-vous la formule pour l'aire d'un triangle. L'aire de tout triangle est égale à 1/2 fois la longueur de la base (qui, dans le polygone, est la longueur d'un côté) multipliée par la hauteur (qui est la même que l'apothème en polygone régulier).[3]  3 Voir les similitudes. Encore une fois, la formule pour un polygone régulier est 1/2 fois plus grande que l'apothème multiplié par le périmètre. Le périmètre est juste la longueur d'un côté multiplié par le nombre de côtés (n); pour un polygone régulier, n représente également le nombre de triangles qui composent la figure. La formule n'est donc rien d'autre que l'aire d'un triangle multipliée par le nombre de triangles du polygone.[4]
3 Voir les similitudes. Encore une fois, la formule pour un polygone régulier est 1/2 fois plus grande que l'apothème multiplié par le périmètre. Le périmètre est juste la longueur d'un côté multiplié par le nombre de côtés (n); pour un polygone régulier, n représente également le nombre de triangles qui composent la figure. La formule n'est donc rien d'autre que l'aire d'un triangle multipliée par le nombre de triangles du polygone.[4]