Tous les triangles rectangles ont un angle droit (90 degrés) et l'hypoténuse est le côté opposé ou droit ou le plus long du triangle rectangle.[1] L'hypoténuse est le côté le plus long du triangle, et il est également très facile de trouver différentes méthodes. Cet article vous apprendra à trouver la longueur de l'hypoténuse en utilisant le théorème de Pythagore lorsque vous connaissez la longueur des deux autres côtés du triangle. Il vous apprendra ensuite à reconnaître l'hypoténuse de certains triangles rectangles spéciaux qui apparaissent souvent sur les tests. Il vous apprendra finalement à trouver la longueur de l'hypoténuse en utilisant la loi des sinus quand vous ne connaissez que la longueur d'un côté et la mesure d'un angle supplémentaire.
Méthode One of Three:
Utilisation du théorème de Pythagore
-
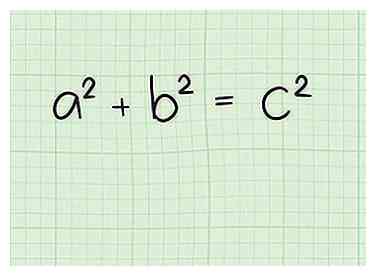 1 Apprenez le théorème de Pythagore. Le théorème de Pythagore décrit la relation entre les côtés d'un triangle rectangle.[2] Il indique que pour tout triangle rectangle ayant des côtés de longueur a et b et une hypoténuse de longueur c, une2 + b2 = c2.[3]
1 Apprenez le théorème de Pythagore. Le théorème de Pythagore décrit la relation entre les côtés d'un triangle rectangle.[2] Il indique que pour tout triangle rectangle ayant des côtés de longueur a et b et une hypoténuse de longueur c, une2 + b2 = c2.[3] -
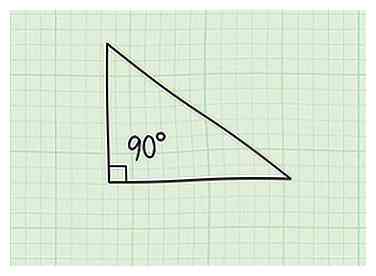 2 Assurez-vous que votre triangle est un triangle rectangle. Le théorème de Pythagore ne fonctionne que sur les triangles rectangles et, par définition, seuls les triangles droits peuvent avoir une hypoténuse. Si votre triangle contient un angle de 90 degrés exactement, c'est un triangle rectangle et vous pouvez continuer.
2 Assurez-vous que votre triangle est un triangle rectangle. Le théorème de Pythagore ne fonctionne que sur les triangles rectangles et, par définition, seuls les triangles droits peuvent avoir une hypoténuse. Si votre triangle contient un angle de 90 degrés exactement, c'est un triangle rectangle et vous pouvez continuer. - Les angles droits sont souvent notés dans les manuels et lors des tests avec un petit carré dans le coin de l’angle. Cette marque spéciale signifie "90 degrés".
-
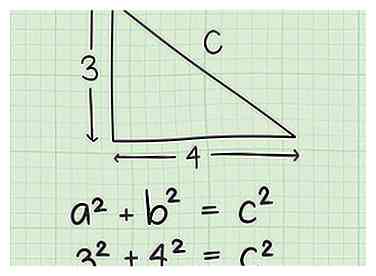 3 Attribuez les variables a, b et c aux côtés de votre triangle. La variable "c" sera toujours affectée à l'hypoténuse ou au côté le plus long. Choisissez l'un des autres côtés à être une, et appelle l'autre côté b (peu importe lequel, le calcul sera le même). Ensuite, copiez les longueurs de a et b dans la formule, selon l'exemple suivant:
3 Attribuez les variables a, b et c aux côtés de votre triangle. La variable "c" sera toujours affectée à l'hypoténuse ou au côté le plus long. Choisissez l'un des autres côtés à être une, et appelle l'autre côté b (peu importe lequel, le calcul sera le même). Ensuite, copiez les longueurs de a et b dans la formule, selon l'exemple suivant: - Si votre triangle a des côtés de 3 et 4, et que vous avez attribué des lettres à ces côtés telles que a = 3 et b = 4, vous devez alors écrire votre équation comme suit: 32 + 42 = c2.
-
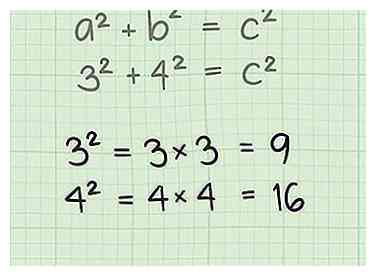 4 Trouvez les carrés de a et b. Pour trouver le carré d'un nombre, il vous suffit de multiplier le nombre par lui-même, donc une2 = a x a. Trouvez les carrés à la fois a et b et écrivez-les dans votre formule.
4 Trouvez les carrés de a et b. Pour trouver le carré d'un nombre, il vous suffit de multiplier le nombre par lui-même, donc une2 = a x a. Trouvez les carrés à la fois a et b et écrivez-les dans votre formule. - Si a = 3, a2 = 3 x 3 ou 9. Si b = 4, alors b2 = 4 x 4 ou 16.
- Lorsque vous branchez ces valeurs dans votre équation, il devrait maintenant ressembler à ceci: 9 + 16 = c2.
-
 5 Ajouter ensemble les valeurs de une2 et b2. Entrez ceci dans votre équation, et cela vous donnera la valeur pour c2. Il ne reste plus qu'un pas à faire et vous aurez cette hypoténuse résolue!
5 Ajouter ensemble les valeurs de une2 et b2. Entrez ceci dans votre équation, et cela vous donnera la valeur pour c2. Il ne reste plus qu'un pas à faire et vous aurez cette hypoténuse résolue! - Dans notre exemple, 9 + 16 = 25, donc vous devriez écrire 25 = c2.
-
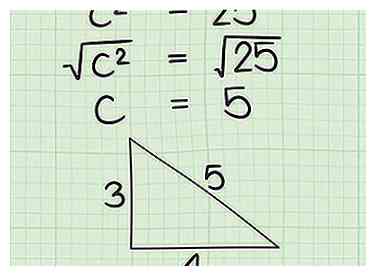 6 Trouvez la racine carrée de c2. Utilisez la fonction racine carrée de votre calculatrice (ou votre mémoire de la table de multiplication) pour trouver la racine carrée de c2. La réponse est la longueur de votre hypoténuse!
6 Trouvez la racine carrée de c2. Utilisez la fonction racine carrée de votre calculatrice (ou votre mémoire de la table de multiplication) pour trouver la racine carrée de c2. La réponse est la longueur de votre hypoténuse! - Dans notre exemple, c2 = 25. La racine carrée de 25 est 5 (5 x 5 = 25, alors Sqrt (25) = 5). Cela signifie c = 5, la longueur de notre hypoténuse!
Méthode deux sur trois:
Trouver l'hypoténuse des triangles spéciaux
-
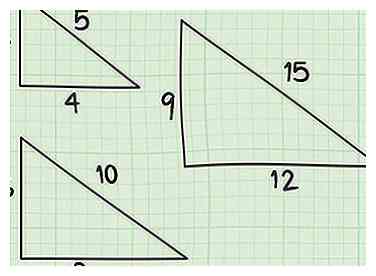 1 Apprenez à reconnaître les triples triangles de Pythagore. Les longueurs latérales d'un triple de Pythagore sont des nombres entiers qui correspondent au théorème de Pythagore. Ces triangles spéciaux apparaissent fréquemment dans les manuels de géométrie et sur des tests standardisés tels que le SAT et le GRE. Si vous mémorisez les deux premiers triplets de Pythagore, en particulier, vous pouvez vous épargner beaucoup de temps sur ces tests, car vous pouvez immédiatement connaître l’hypoténuse de l’un de ces triangles en regardant simplement les côtés! [4]
1 Apprenez à reconnaître les triples triangles de Pythagore. Les longueurs latérales d'un triple de Pythagore sont des nombres entiers qui correspondent au théorème de Pythagore. Ces triangles spéciaux apparaissent fréquemment dans les manuels de géométrie et sur des tests standardisés tels que le SAT et le GRE. Si vous mémorisez les deux premiers triplets de Pythagore, en particulier, vous pouvez vous épargner beaucoup de temps sur ces tests, car vous pouvez immédiatement connaître l’hypoténuse de l’un de ces triangles en regardant simplement les côtés! [4] - Le premier triple pythagoricien est 3-4-5 (32 + 42 = 52, 9 + 16 = 25). Lorsque vous voyez un triangle rectangle avec des jambes de longueur 3 et 4, vous pouvez être certain que l’hypoténuse sera de 5 sans avoir à faire de calculs.
- Le ratio d'un triple de Pythagore est vrai même lorsque les côtés sont multipliés par un autre nombre. Par exemple un triangle rectangle avec des jambes de longueur 6 et 8 aura une hypoténuse de 10 (62 + 82 = 102, 36 + 64 = 100). La même chose vaut pour 9-12-15, et même 1.5-2-2.5. Essayez les maths et voyez par vous-même!
- Le deuxième triplet pythagoricien qui apparaît couramment sur les tests est 5-12-13 (52 + 122 = 132, 25 + 144 = 169). Soyez également à l'affût de multiples comme 10-24-26 et 2.5-6-6.5.
-
 2 Mémorisez les rapports latéraux d'un triangle rectangle 45-45-90. Un triangle rectangle 45-45-90 a des angles de 45, 45 et 90 degrés et est également appelé triangle droit Isosceles. Il se produit fréquemment sur des tests standardisés et constitue un triangle très facile à résoudre. Le rapport entre les côtés de ce triangle est 1: 1: Sqrt (2), ce qui signifie que la longueur des jambes est égale et que la longueur de l'hypoténuse est simplement la longueur de la jambe multipliée par la racine carrée de deux.
2 Mémorisez les rapports latéraux d'un triangle rectangle 45-45-90. Un triangle rectangle 45-45-90 a des angles de 45, 45 et 90 degrés et est également appelé triangle droit Isosceles. Il se produit fréquemment sur des tests standardisés et constitue un triangle très facile à résoudre. Le rapport entre les côtés de ce triangle est 1: 1: Sqrt (2), ce qui signifie que la longueur des jambes est égale et que la longueur de l'hypoténuse est simplement la longueur de la jambe multipliée par la racine carrée de deux. - Pour calculer l'hypoténuse de ce triangle en fonction de la longueur de l'une des jambes, multipliez simplement la longueur de jambe par Sqrt (2).[5]
- Connaître ce ratio est particulièrement utile lorsque votre question de test ou de devoir vous donne les longueurs latérales en termes de variables et non de nombres entiers.
-
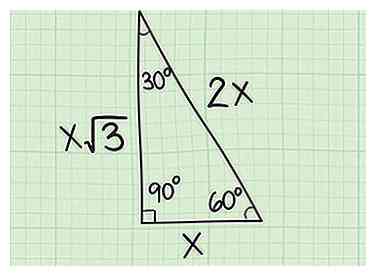 3 Apprenez les ratios latéraux d'un triangle rectangle 30-60-90. Ce triangle a des mesures d'angle de 30, 60 et 90 degrés et se produit lorsque vous coupez un triangle équilatéral en deux. Les côtés du triangle rectangle 30-60-90 maintiennent toujours le rapport 1: Sqrt (3): 2, ou x: Sqrt (3) x: 2x. Si on vous donne la longueur d'une jambe du triangle rectangle 30-60-90 et qu'on vous demande de trouver l'hypoténuse, c'est très facile à faire:[6]
3 Apprenez les ratios latéraux d'un triangle rectangle 30-60-90. Ce triangle a des mesures d'angle de 30, 60 et 90 degrés et se produit lorsque vous coupez un triangle équilatéral en deux. Les côtés du triangle rectangle 30-60-90 maintiennent toujours le rapport 1: Sqrt (3): 2, ou x: Sqrt (3) x: 2x. Si on vous donne la longueur d'une jambe du triangle rectangle 30-60-90 et qu'on vous demande de trouver l'hypoténuse, c'est très facile à faire:[6] - Si on vous donne la longueur de la jambe la plus courte (à l'opposé de l'angle de 30 degrés), multipliez simplement la longueur de la jambe par 2 pour trouver la longueur de l'hypoténuse. Par exemple, si la longueur de la jambe la plus courte est 4, vous savez que la longueur de l'hypoténuse doit être 8.
- Si on vous donne la longueur de la jambe la plus longue (à l'opposé de l'angle de 60 degrés), multipliez cette longueur par 2 / Sqrt (3) trouver la longueur de l'hypoténuse. Par exemple, si la longueur de la jambe la plus longue est 4, vous savez que la longueur de l'hypoténuse doit être 4.62.
Méthode trois sur trois:
Trouver l'hypoténuse en utilisant la loi des sinus
-
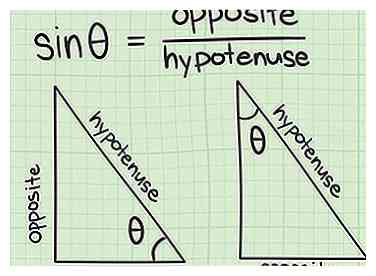 1 Comprendre ce que signifie "Sine". Les termes "sinus", "cosinus" et "tangente" font tous référence à divers rapports entre les angles et / ou les côtés d'un triangle rectangle. Dans un triangle rectangle, le sinus d'un angle est défini comme la longueur du côté opposé à l'angle divisé par l'hypoténuse du triangle. L'abréviation de sinus trouvée dans les équations et sur les calculatrices est péché.[7]
1 Comprendre ce que signifie "Sine". Les termes "sinus", "cosinus" et "tangente" font tous référence à divers rapports entre les angles et / ou les côtés d'un triangle rectangle. Dans un triangle rectangle, le sinus d'un angle est défini comme la longueur du côté opposé à l'angle divisé par l'hypoténuse du triangle. L'abréviation de sinus trouvée dans les équations et sur les calculatrices est péché.[7] -
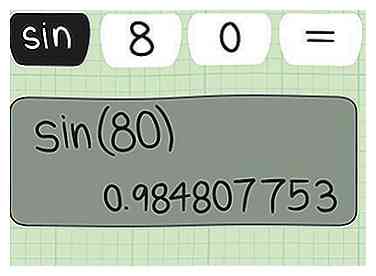 2 Apprenez à calculer le sinus. Même une calculatrice scientifique de base aura une fonction sinusoïdale. Recherchez une clé marquée péché. Pour trouver le sinus d’angle, vous appuierez généralement sur péché puis entrez la mesure de l’angle en degrés. Sur certaines calculatrices, cependant, vous devez d'abord saisir la mesure du degré, puis la péché clé. Vous devrez expérimenter avec votre calculatrice ou consulter le manuel pour savoir lequel.
2 Apprenez à calculer le sinus. Même une calculatrice scientifique de base aura une fonction sinusoïdale. Recherchez une clé marquée péché. Pour trouver le sinus d’angle, vous appuierez généralement sur péché puis entrez la mesure de l’angle en degrés. Sur certaines calculatrices, cependant, vous devez d'abord saisir la mesure du degré, puis la péché clé. Vous devrez expérimenter avec votre calculatrice ou consulter le manuel pour savoir lequel. - Pour trouver le sinus d'un angle de 80 degrés, vous devrez soit saisir péché 80 suivi du signe égal ou de la touche Entrée, ou 80 péché. (La réponse est -0.9939.)
- Vous pouvez également taper «calculatrice sinusoïdale» dans une recherche sur le Web et trouver un certain nombre de calculatrices faciles à utiliser qui élimineront toute conjecture.[8]
-
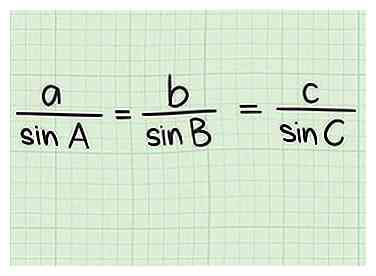 3 Apprenez la loi des sinus. La loi des sinus est un outil utile pour résoudre des triangles. En particulier, il peut vous aider à trouver l'hypoténuse d'un triangle rectangle si vous connaissez la longueur d'un côté et la mesure d'un autre angle en plus de l'angle droit. Pour tout triangle avec des côtés une, b, et cet angles UNE, B, et C, la loi des sinus affirme que une / péché UNE = b / péché B = c / péché C.[9]
3 Apprenez la loi des sinus. La loi des sinus est un outil utile pour résoudre des triangles. En particulier, il peut vous aider à trouver l'hypoténuse d'un triangle rectangle si vous connaissez la longueur d'un côté et la mesure d'un autre angle en plus de l'angle droit. Pour tout triangle avec des côtés une, b, et cet angles UNE, B, et C, la loi des sinus affirme que une / péché UNE = b / péché B = c / péché C.[9] - La loi des sinus peut être utilisée pour résoudre tout triangle, mais seul un triangle rectangle aura une hypoténuse.
-
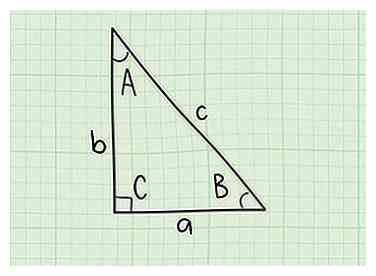 4 Attribuez les variables a, b et c aux côtés de votre triangle. L'hypoténuse (côté le plus long) doit être "c". Par souci de simplicité, étiquetez le côté de la longueur connue comme "a" et l'autre "b". Puis attribuez les variables A, B et C aux angles du triangle. L'angle droit opposé à l'hypoténuse sera "C". L'angle opposé "a" est l'angle "A" et l'angle opposé "b" est "B".
4 Attribuez les variables a, b et c aux côtés de votre triangle. L'hypoténuse (côté le plus long) doit être "c". Par souci de simplicité, étiquetez le côté de la longueur connue comme "a" et l'autre "b". Puis attribuez les variables A, B et C aux angles du triangle. L'angle droit opposé à l'hypoténuse sera "C". L'angle opposé "a" est l'angle "A" et l'angle opposé "b" est "B". -
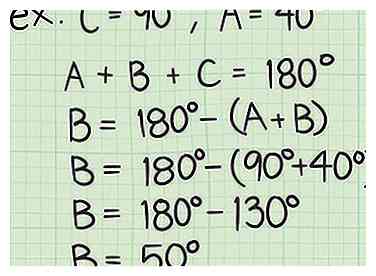 5 Calculez la mesure du troisième angle. Parce que c'est un angle droit, vous savez déjà que C = 90 degrés, et vous connaissez aussi la mesure de UNE ou B. Comme la mesure de degré interne d'un triangle doit toujours être égale à 180 degrés, vous pouvez facilement calculer la mesure du troisième angle à l'aide de la formule suivante: 180 - (90 + A) = B. Vous pouvez également inverser l'équation de telle sorte que 180 - (90 + B) = A.
5 Calculez la mesure du troisième angle. Parce que c'est un angle droit, vous savez déjà que C = 90 degrés, et vous connaissez aussi la mesure de UNE ou B. Comme la mesure de degré interne d'un triangle doit toujours être égale à 180 degrés, vous pouvez facilement calculer la mesure du troisième angle à l'aide de la formule suivante: 180 - (90 + A) = B. Vous pouvez également inverser l'équation de telle sorte que 180 - (90 + B) = A. - Par exemple, si vous savez que A = 40 degrés, puis B = 180 - (90 + 40). Simplifiez cela pour B = 180 - 130, et vous pouvez rapidement déterminer que B = 50 degrés.
-
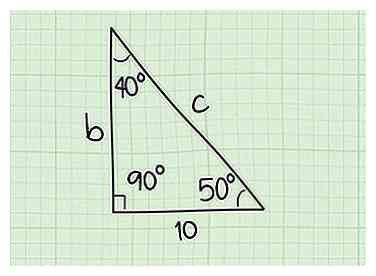 6 Examine ton triangle. À ce stade, vous devez connaître le degré de mesure des trois angles et la longueur du côté a. Il est maintenant temps d'insérer cette information dans l'équation de la loi des sinus pour déterminer la longueur des deux autres côtés.
6 Examine ton triangle. À ce stade, vous devez connaître le degré de mesure des trois angles et la longueur du côté a. Il est maintenant temps d'insérer cette information dans l'équation de la loi des sinus pour déterminer la longueur des deux autres côtés. - Pour continuer notre exemple, disons que la longueur du côté a = 10. Angle C = 90 degrés, angle A = 40 degrés et angle B = 50 degrés.
-
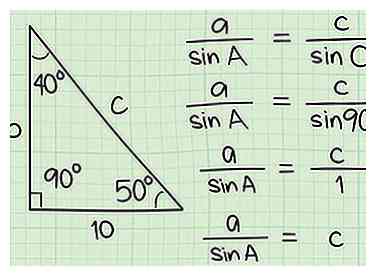 7 Appliquez la loi des sinus à votre triangle. Il suffit de brancher nos chiffres et de résoudre l'équation suivante pour déterminer la longueur de l'hypoténuse c: longueur de côté a / péché A = longueur du côté c / péché C. Cela peut sembler un peu intimidant, mais le sinus de 90 degrés est une constante, et est toujours égal à 1! Notre équation peut donc être simplifiée pour: une / péché A = c / 1, ou juste une / péché A = c.
7 Appliquez la loi des sinus à votre triangle. Il suffit de brancher nos chiffres et de résoudre l'équation suivante pour déterminer la longueur de l'hypoténuse c: longueur de côté a / péché A = longueur du côté c / péché C. Cela peut sembler un peu intimidant, mais le sinus de 90 degrés est une constante, et est toujours égal à 1! Notre équation peut donc être simplifiée pour: une / péché A = c / 1, ou juste une / péché A = c. -
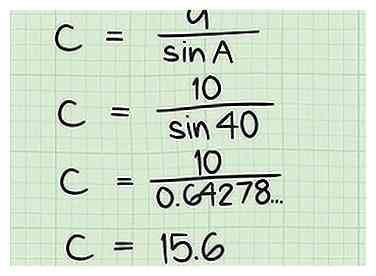 8 Diviser la longueur du côté une par le sinus de l'angle UNE trouver la longueur de l'hypoténuse! Vous pouvez le faire en deux étapes distinctes, en calculant d'abord péché A et en l'écrivant, puis en divisant par a. Ou vous pouvez tout saisir dans la calculatrice en même temps. Si vous le faites, n'oubliez pas d'inclure les parenthèses après le signe de division. Par exemple, entrez soit 10 / (péché 40) ou 10 / (40 péché), en fonction de votre calculatrice.
8 Diviser la longueur du côté une par le sinus de l'angle UNE trouver la longueur de l'hypoténuse! Vous pouvez le faire en deux étapes distinctes, en calculant d'abord péché A et en l'écrivant, puis en divisant par a. Ou vous pouvez tout saisir dans la calculatrice en même temps. Si vous le faites, n'oubliez pas d'inclure les parenthèses après le signe de division. Par exemple, entrez soit 10 / (péché 40) ou 10 / (40 péché), en fonction de votre calculatrice. - En utilisant notre exemple, nous trouvons que péché 40 = 0,64278761. Pour trouver la valeur de c, il suffit de diviser la longueur d'un par ce nombre et d'apprendre que 10 / 0.64278761 = 15.6, la longueur de notre hypoténuse!
 Minotauromaquia
Minotauromaquia
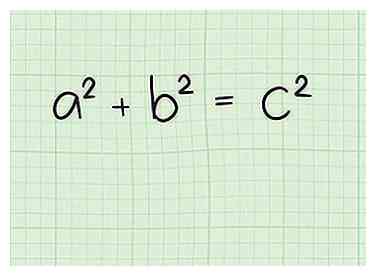 1 Apprenez le théorème de Pythagore. Le théorème de Pythagore décrit la relation entre les côtés d'un triangle rectangle.[2] Il indique que pour tout triangle rectangle ayant des côtés de longueur a et b et une hypoténuse de longueur c, une2 + b2 = c2.[3]
1 Apprenez le théorème de Pythagore. Le théorème de Pythagore décrit la relation entre les côtés d'un triangle rectangle.[2] Il indique que pour tout triangle rectangle ayant des côtés de longueur a et b et une hypoténuse de longueur c, une2 + b2 = c2.[3]  2 Assurez-vous que votre triangle est un triangle rectangle. Le théorème de Pythagore ne fonctionne que sur les triangles rectangles et, par définition, seuls les triangles droits peuvent avoir une hypoténuse. Si votre triangle contient un angle de 90 degrés exactement, c'est un triangle rectangle et vous pouvez continuer.
2 Assurez-vous que votre triangle est un triangle rectangle. Le théorème de Pythagore ne fonctionne que sur les triangles rectangles et, par définition, seuls les triangles droits peuvent avoir une hypoténuse. Si votre triangle contient un angle de 90 degrés exactement, c'est un triangle rectangle et vous pouvez continuer.  3 Attribuez les variables a, b et c aux côtés de votre triangle. La variable "c" sera toujours affectée à l'hypoténuse ou au côté le plus long. Choisissez l'un des autres côtés à être une, et appelle l'autre côté b (peu importe lequel, le calcul sera le même). Ensuite, copiez les longueurs de a et b dans la formule, selon l'exemple suivant:
3 Attribuez les variables a, b et c aux côtés de votre triangle. La variable "c" sera toujours affectée à l'hypoténuse ou au côté le plus long. Choisissez l'un des autres côtés à être une, et appelle l'autre côté b (peu importe lequel, le calcul sera le même). Ensuite, copiez les longueurs de a et b dans la formule, selon l'exemple suivant: 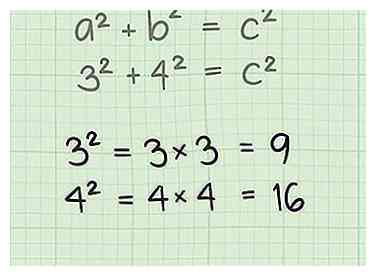 4 Trouvez les carrés de a et b. Pour trouver le carré d'un nombre, il vous suffit de multiplier le nombre par lui-même, donc une2 = a x a. Trouvez les carrés à la fois a et b et écrivez-les dans votre formule.
4 Trouvez les carrés de a et b. Pour trouver le carré d'un nombre, il vous suffit de multiplier le nombre par lui-même, donc une2 = a x a. Trouvez les carrés à la fois a et b et écrivez-les dans votre formule.  5 Ajouter ensemble les valeurs de une2 et b2. Entrez ceci dans votre équation, et cela vous donnera la valeur pour c2. Il ne reste plus qu'un pas à faire et vous aurez cette hypoténuse résolue!
5 Ajouter ensemble les valeurs de une2 et b2. Entrez ceci dans votre équation, et cela vous donnera la valeur pour c2. Il ne reste plus qu'un pas à faire et vous aurez cette hypoténuse résolue! 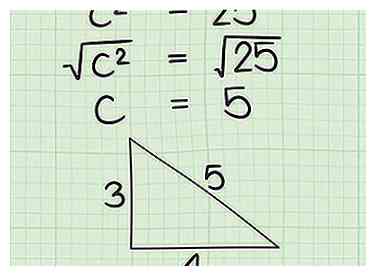 6 Trouvez la racine carrée de c2. Utilisez la fonction racine carrée de votre calculatrice (ou votre mémoire de la table de multiplication) pour trouver la racine carrée de c2. La réponse est la longueur de votre hypoténuse!
6 Trouvez la racine carrée de c2. Utilisez la fonction racine carrée de votre calculatrice (ou votre mémoire de la table de multiplication) pour trouver la racine carrée de c2. La réponse est la longueur de votre hypoténuse!  1 Apprenez à reconnaître les triples triangles de Pythagore. Les longueurs latérales d'un triple de Pythagore sont des nombres entiers qui correspondent au théorème de Pythagore. Ces triangles spéciaux apparaissent fréquemment dans les manuels de géométrie et sur des tests standardisés tels que le SAT et le GRE. Si vous mémorisez les deux premiers triplets de Pythagore, en particulier, vous pouvez vous épargner beaucoup de temps sur ces tests, car vous pouvez immédiatement connaître l’hypoténuse de l’un de ces triangles en regardant simplement les côtés! [4]
1 Apprenez à reconnaître les triples triangles de Pythagore. Les longueurs latérales d'un triple de Pythagore sont des nombres entiers qui correspondent au théorème de Pythagore. Ces triangles spéciaux apparaissent fréquemment dans les manuels de géométrie et sur des tests standardisés tels que le SAT et le GRE. Si vous mémorisez les deux premiers triplets de Pythagore, en particulier, vous pouvez vous épargner beaucoup de temps sur ces tests, car vous pouvez immédiatement connaître l’hypoténuse de l’un de ces triangles en regardant simplement les côtés! [4]  2 Mémorisez les rapports latéraux d'un triangle rectangle 45-45-90. Un triangle rectangle 45-45-90 a des angles de 45, 45 et 90 degrés et est également appelé triangle droit Isosceles. Il se produit fréquemment sur des tests standardisés et constitue un triangle très facile à résoudre. Le rapport entre les côtés de ce triangle est 1: 1: Sqrt (2), ce qui signifie que la longueur des jambes est égale et que la longueur de l'hypoténuse est simplement la longueur de la jambe multipliée par la racine carrée de deux.
2 Mémorisez les rapports latéraux d'un triangle rectangle 45-45-90. Un triangle rectangle 45-45-90 a des angles de 45, 45 et 90 degrés et est également appelé triangle droit Isosceles. Il se produit fréquemment sur des tests standardisés et constitue un triangle très facile à résoudre. Le rapport entre les côtés de ce triangle est 1: 1: Sqrt (2), ce qui signifie que la longueur des jambes est égale et que la longueur de l'hypoténuse est simplement la longueur de la jambe multipliée par la racine carrée de deux.  3 Apprenez les ratios latéraux d'un triangle rectangle 30-60-90. Ce triangle a des mesures d'angle de 30, 60 et 90 degrés et se produit lorsque vous coupez un triangle équilatéral en deux. Les côtés du triangle rectangle 30-60-90 maintiennent toujours le rapport 1: Sqrt (3): 2, ou x: Sqrt (3) x: 2x. Si on vous donne la longueur d'une jambe du triangle rectangle 30-60-90 et qu'on vous demande de trouver l'hypoténuse, c'est très facile à faire:[6]
3 Apprenez les ratios latéraux d'un triangle rectangle 30-60-90. Ce triangle a des mesures d'angle de 30, 60 et 90 degrés et se produit lorsque vous coupez un triangle équilatéral en deux. Les côtés du triangle rectangle 30-60-90 maintiennent toujours le rapport 1: Sqrt (3): 2, ou x: Sqrt (3) x: 2x. Si on vous donne la longueur d'une jambe du triangle rectangle 30-60-90 et qu'on vous demande de trouver l'hypoténuse, c'est très facile à faire:[6]  1 Comprendre ce que signifie "Sine". Les termes "sinus", "cosinus" et "tangente" font tous référence à divers rapports entre les angles et / ou les côtés d'un triangle rectangle. Dans un triangle rectangle, le sinus d'un angle est défini comme la longueur du côté opposé à l'angle divisé par l'hypoténuse du triangle. L'abréviation de sinus trouvée dans les équations et sur les calculatrices est péché.[7]
1 Comprendre ce que signifie "Sine". Les termes "sinus", "cosinus" et "tangente" font tous référence à divers rapports entre les angles et / ou les côtés d'un triangle rectangle. Dans un triangle rectangle, le sinus d'un angle est défini comme la longueur du côté opposé à l'angle divisé par l'hypoténuse du triangle. L'abréviation de sinus trouvée dans les équations et sur les calculatrices est péché.[7]  2 Apprenez à calculer le sinus. Même une calculatrice scientifique de base aura une fonction sinusoïdale. Recherchez une clé marquée péché. Pour trouver le sinus d’angle, vous appuierez généralement sur péché puis entrez la mesure de l’angle en degrés. Sur certaines calculatrices, cependant, vous devez d'abord saisir la mesure du degré, puis la péché clé. Vous devrez expérimenter avec votre calculatrice ou consulter le manuel pour savoir lequel.
2 Apprenez à calculer le sinus. Même une calculatrice scientifique de base aura une fonction sinusoïdale. Recherchez une clé marquée péché. Pour trouver le sinus d’angle, vous appuierez généralement sur péché puis entrez la mesure de l’angle en degrés. Sur certaines calculatrices, cependant, vous devez d'abord saisir la mesure du degré, puis la péché clé. Vous devrez expérimenter avec votre calculatrice ou consulter le manuel pour savoir lequel. 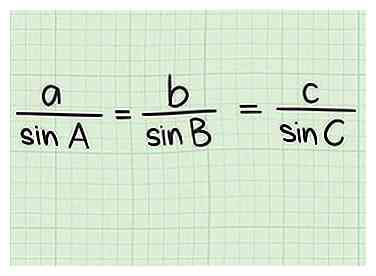 3 Apprenez la loi des sinus. La loi des sinus est un outil utile pour résoudre des triangles. En particulier, il peut vous aider à trouver l'hypoténuse d'un triangle rectangle si vous connaissez la longueur d'un côté et la mesure d'un autre angle en plus de l'angle droit. Pour tout triangle avec des côtés une, b, et cet angles UNE, B, et C, la loi des sinus affirme que une / péché UNE = b / péché B = c / péché C.[9]
3 Apprenez la loi des sinus. La loi des sinus est un outil utile pour résoudre des triangles. En particulier, il peut vous aider à trouver l'hypoténuse d'un triangle rectangle si vous connaissez la longueur d'un côté et la mesure d'un autre angle en plus de l'angle droit. Pour tout triangle avec des côtés une, b, et cet angles UNE, B, et C, la loi des sinus affirme que une / péché UNE = b / péché B = c / péché C.[9]  4 Attribuez les variables a, b et c aux côtés de votre triangle. L'hypoténuse (côté le plus long) doit être "c". Par souci de simplicité, étiquetez le côté de la longueur connue comme "a" et l'autre "b". Puis attribuez les variables A, B et C aux angles du triangle. L'angle droit opposé à l'hypoténuse sera "C". L'angle opposé "a" est l'angle "A" et l'angle opposé "b" est "B".
4 Attribuez les variables a, b et c aux côtés de votre triangle. L'hypoténuse (côté le plus long) doit être "c". Par souci de simplicité, étiquetez le côté de la longueur connue comme "a" et l'autre "b". Puis attribuez les variables A, B et C aux angles du triangle. L'angle droit opposé à l'hypoténuse sera "C". L'angle opposé "a" est l'angle "A" et l'angle opposé "b" est "B". 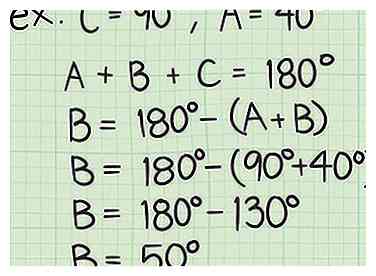 5 Calculez la mesure du troisième angle. Parce que c'est un angle droit, vous savez déjà que C = 90 degrés, et vous connaissez aussi la mesure de UNE ou B. Comme la mesure de degré interne d'un triangle doit toujours être égale à 180 degrés, vous pouvez facilement calculer la mesure du troisième angle à l'aide de la formule suivante: 180 - (90 + A) = B. Vous pouvez également inverser l'équation de telle sorte que 180 - (90 + B) = A.
5 Calculez la mesure du troisième angle. Parce que c'est un angle droit, vous savez déjà que C = 90 degrés, et vous connaissez aussi la mesure de UNE ou B. Comme la mesure de degré interne d'un triangle doit toujours être égale à 180 degrés, vous pouvez facilement calculer la mesure du troisième angle à l'aide de la formule suivante: 180 - (90 + A) = B. Vous pouvez également inverser l'équation de telle sorte que 180 - (90 + B) = A.  6 Examine ton triangle. À ce stade, vous devez connaître le degré de mesure des trois angles et la longueur du côté a. Il est maintenant temps d'insérer cette information dans l'équation de la loi des sinus pour déterminer la longueur des deux autres côtés.
6 Examine ton triangle. À ce stade, vous devez connaître le degré de mesure des trois angles et la longueur du côté a. Il est maintenant temps d'insérer cette information dans l'équation de la loi des sinus pour déterminer la longueur des deux autres côtés.  7 Appliquez la loi des sinus à votre triangle. Il suffit de brancher nos chiffres et de résoudre l'équation suivante pour déterminer la longueur de l'hypoténuse c: longueur de côté a / péché A = longueur du côté c / péché C. Cela peut sembler un peu intimidant, mais le sinus de 90 degrés est une constante, et est toujours égal à 1! Notre équation peut donc être simplifiée pour: une / péché A = c / 1, ou juste une / péché A = c.
7 Appliquez la loi des sinus à votre triangle. Il suffit de brancher nos chiffres et de résoudre l'équation suivante pour déterminer la longueur de l'hypoténuse c: longueur de côté a / péché A = longueur du côté c / péché C. Cela peut sembler un peu intimidant, mais le sinus de 90 degrés est une constante, et est toujours égal à 1! Notre équation peut donc être simplifiée pour: une / péché A = c / 1, ou juste une / péché A = c. 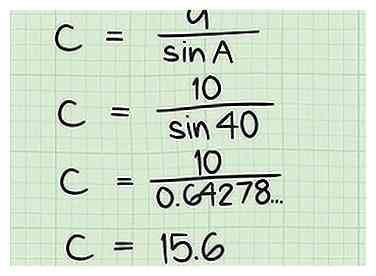 8 Diviser la longueur du côté une par le sinus de l'angle UNE trouver la longueur de l'hypoténuse! Vous pouvez le faire en deux étapes distinctes, en calculant d'abord péché A et en l'écrivant, puis en divisant par a. Ou vous pouvez tout saisir dans la calculatrice en même temps. Si vous le faites, n'oubliez pas d'inclure les parenthèses après le signe de division. Par exemple, entrez soit 10 / (péché 40) ou 10 / (40 péché), en fonction de votre calculatrice.
8 Diviser la longueur du côté une par le sinus de l'angle UNE trouver la longueur de l'hypoténuse! Vous pouvez le faire en deux étapes distinctes, en calculant d'abord péché A et en l'écrivant, puis en divisant par a. Ou vous pouvez tout saisir dans la calculatrice en même temps. Si vous le faites, n'oubliez pas d'inclure les parenthèses après le signe de division. Par exemple, entrez soit 10 / (péché 40) ou 10 / (40 péché), en fonction de votre calculatrice.