Pour trouver l'équation d'une ligne, vous avez le choix entre plusieurs options en fonction de ce que vous recevez. Vous aurez toujours besoin au moins de un point sur la ligne et la pente pour calculer une équation. Bien que la tâche puisse parfois sembler insurmontable, les différents processus sont vraiment faciles une fois que vous savez ce que vous recherchez. Une fois que vous avez le point et la pente de votre ligne, le reste est juste branché et réorganisé.
Méthode One of Four:
Utiliser les points donnés pour une pente
-
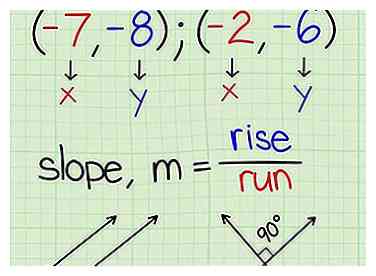 1 Voir si on vous donne 2 points ou 1 point et la pente. Si on vous donne 1 point sur la ligne et sa pente, vous pouvez continuer jusqu'à la Finir avec la formule Point-Slope méthode. Sinon, vous devrez utiliser les deux points donnés pour trouver la pente de la ligne.
1 Voir si on vous donne 2 points ou 1 point et la pente. Si on vous donne 1 point sur la ligne et sa pente, vous pouvez continuer jusqu'à la Finir avec la formule Point-Slope méthode. Sinon, vous devrez utiliser les deux points donnés pour trouver la pente de la ligne. - Ils seront sous la forme de (X1, y1) et (X2, y2).
-
 2 Utilisez toute autre information pour obtenir des points sur la ligne. Certains problèmes nécessitent une interprétation des informations sur la ligne pour obtenir un point sur la ligne. Par exemple, si on vous dit que la ligne traverse le origine, Tu le sais (0, 0) est un point sur la ligne!
2 Utilisez toute autre information pour obtenir des points sur la ligne. Certains problèmes nécessitent une interprétation des informations sur la ligne pour obtenir un point sur la ligne. Par exemple, si on vous dit que la ligne traverse le origine, Tu le sais (0, 0) est un point sur la ligne! - Jetez un oeil à tous les graphiques qui sont avec la question au cas où vous êtes censé trouver une interception (où la ligne traverse le axe des x ou axe y) de la photo. Un x-intercepter serait sous la forme (a, 0) alors qu'un intercepter serait (0, b).
- On pourrait aussi simplement dire que la ligne traverse un axe à un point donné. Cela signifie définir le correspondant X ou y valeur à 0, et le jumeler avec le nombre donné où la ligne croise.
-
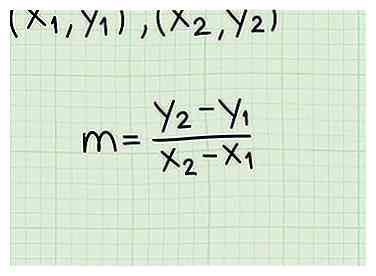 3 Calculez la pente de la ligne par les deux points. L'équation de la pente est m = (y2 - y1) / (X2 - X1). En branchant simplement vos points de coordonnées et en résolvant, vous connaissez maintenant la pente de l'équation.
3 Calculez la pente de la ligne par les deux points. L'équation de la pente est m = (y2 - y1) / (X2 - X1). En branchant simplement vos points de coordonnées et en résolvant, vous connaissez maintenant la pente de l'équation. - La pente est presque toujours appelée m. Soyez conscient que cela peut être positif ou négatif.
- A partir de là, vous aurez seulement besoin de l'un des points que vous avez trouvés avec la pente. Si l'on est apparemment plus simple, optez pour celui-là. Par exemple, si votre ligne traverse le origine, résoudre le reste du problème avec (0, 0) est un peu plus rapide.
Méthode deux sur quatre:
Obtenir la pente d'une autre ligne
-
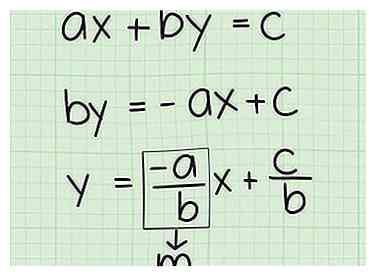 1 Utilisez la même pente si l'autre ligne est parallèle. Les lignes parallèles partagent la même pente, il suffit d'utiliser l'équation de cette ligne pour obtenir la pente de votre première ligne.
1 Utilisez la même pente si l'autre ligne est parallèle. Les lignes parallèles partagent la même pente, il suffit d'utiliser l'équation de cette ligne pour obtenir la pente de votre première ligne. - Utilisez l'algèbre pour organiser l'équation de la ligne en Forme d'interception de pente lequel est y = mx + b. Si y est seul sur le côté gauche, alors m est la pente des deux lignes et b sera juste le intercepter de cette ligne.
- Après avoir organisé l'équation, réalisez que votre pente peut être positive, négative ou même une fraction plutôt qu'un entier.
-
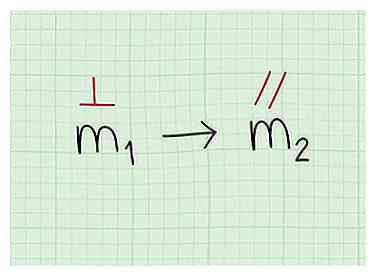 2 Trouvez la pente d'une ligne perpendiculaire. Souvent, les questions vous donneront un perpendiculaire ligne à la ligne que vous voulez une équation pour. Ici, vous utiliserez les mêmes concepts que précédemment pour déterminer la pente de la ligne perpendiculaire.
2 Trouvez la pente d'une ligne perpendiculaire. Souvent, les questions vous donneront un perpendiculaire ligne à la ligne que vous voulez une équation pour. Ici, vous utiliserez les mêmes concepts que précédemment pour déterminer la pente de la ligne perpendiculaire. - Réorganisez simplement l'équation donnée en utilisant l'algèbre pour obtenir l'équation dans Forme d'interception de pente (y = mx + b).
-
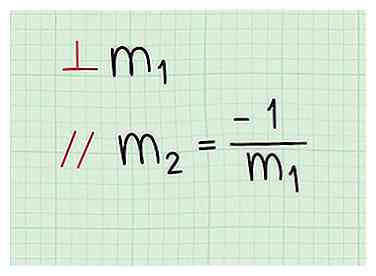 3 Utilisez l'inverse inverse de la pente de la ligne perpendiculaire. Toute ligne perpendiculaire à une autre ligne a une pente qui est la réciproque négative de l'autre ligne. Cela signifie que si la pente d'une ligne est 2, la pente d'une ligne perpendiculaire sera -1/2.
3 Utilisez l'inverse inverse de la pente de la ligne perpendiculaire. Toute ligne perpendiculaire à une autre ligne a une pente qui est la réciproque négative de l'autre ligne. Cela signifie que si la pente d'une ligne est 2, la pente d'une ligne perpendiculaire sera -1/2. - Il suffit de faire deux choses sur la pente pour obtenir la réciproque négative.
- D'abord, retournez le signe. Si la pente est négative, rendez-la positive. Si c'est positif, le rendre négatif.
- Deuxièmement, retournez le numérateur et le dénominateur du numéro. Cela signifie simplement que les chiffres du haut et du bas de la forme de fraction changeront de place. Si la pente n'est pas déjà sous forme de fraction, placez simplement le nombre sur 1. Chaque entier est lui-même divisé par 1.
- Si votre pente est en décimal, changez-la en forme de fraction avant de la retourner.
- La réciproque négative que vous venez de faire est la pente de l'autre ligne!
- La réciproque négative de 4 est -1/4. La réciproque négative de -3/2 est 2/3. La réciproque négative de 1/8 est de -8.
Méthode trois sur quatre:
Finir avec la formule Point-Slope
-
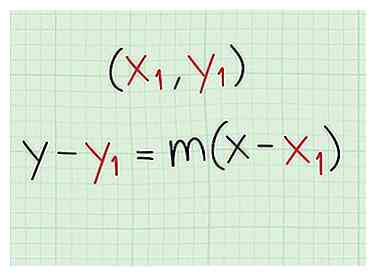 1 Utilisez le formule de pente ponctuelle pour trouver l'équation. Peu importe comment vous êtes arrivé, vous devriez avoir 1 point sur la ligne et la pente de la ligne. La formule à utiliser est y - y1 = m (x - x1). En utilisant la pente m vous venez de calculer et l'une des coordonnées données sur la ligne, branchez les chiffres dans l'équation.
1 Utilisez le formule de pente ponctuelle pour trouver l'équation. Peu importe comment vous êtes arrivé, vous devriez avoir 1 point sur la ligne et la pente de la ligne. La formule à utiliser est y - y1 = m (x - x1). En utilisant la pente m vous venez de calculer et l'une des coordonnées données sur la ligne, branchez les chiffres dans l'équation. - le X et y sans indices restera comme X et y. Vous n'avez pas besoin de substituer quoi que ce soit pour eux.
- Vous pouvez utiliser l'un des points donnés, si vous en avez deux, pour remplacer X1 et y1. L'équation fonctionne pour n'importe quel point de la ligne!
-
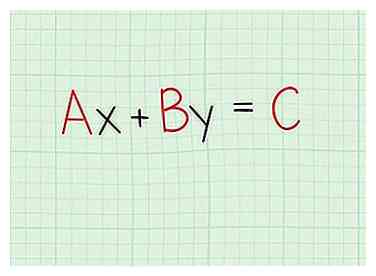 2 Réduire pour formater dans la réponse finale. Certains enseignants recherchent forme standard lequel est Axe + Par = C, où UNE, B, et C sont des coefficients numériques. D'autres voudront Forme d'interception de pente lequel est y = mx + b où m est la pente et b est le intercepter (où la ligne traverse l'axe des y).
2 Réduire pour formater dans la réponse finale. Certains enseignants recherchent forme standard lequel est Axe + Par = C, où UNE, B, et C sont des coefficients numériques. D'autres voudront Forme d'interception de pente lequel est y = mx + b où m est la pente et b est le intercepter (où la ligne traverse l'axe des y). - Pour les deux formes, il vous suffit d'utiliser l'algèbre et de déplacer le X et y variables aux côtés corrects du signe égal.
- Dans Forme d'interception de pente, b travaillera comme le nombre non attaché (multiplié) par X ou y. Ce n'est pas autre chose que vous devrez résoudre ici!
Méthode quatre sur quatre:
Faire face aux pentes irrégulières
-
 1 Prenez une pente de 0 comme bon signe. Si vous avez découvert que la pente est nulle, votre ligne est horizontale! L'équation pour toute ligne avec une pente de 0 est simplement y = b où b est l'endroit où la ligne traverse le axe y.
1 Prenez une pente de 0 comme bon signe. Si vous avez découvert que la pente est nulle, votre ligne est horizontale! L'équation pour toute ligne avec une pente de 0 est simplement y = b où b est l'endroit où la ligne traverse le axe y. - Vous pouvez toujours travailler à travers les équations avec m = 0, mais vous trouverez qu'il se multipliera X par le 0 et réduire considérablement votre équation.
-
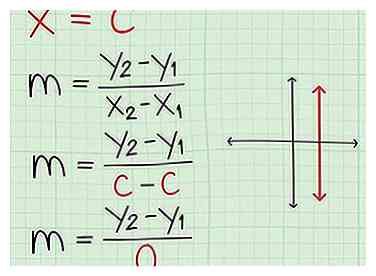 2 Expliquez que la ligne est verticale sinon. Les lignes verticales sont essentiellement le cas contraire. L'équation sera simplement x = c où c est le x-intercepter. Quand une ligne monte directement, elle aura un indéfini pente. C'est parce que quand vous résolvez pour m en utilisant 2 points de ces lignes, vous finirez par diviser par 0.
2 Expliquez que la ligne est verticale sinon. Les lignes verticales sont essentiellement le cas contraire. L'équation sera simplement x = c où c est le x-intercepter. Quand une ligne monte directement, elle aura un indéfini pente. C'est parce que quand vous résolvez pour m en utilisant 2 points de ces lignes, vous finirez par diviser par 0. - Prendre la ligne x = 4. La valeur de n'importe quel point de la ligne est (4, y). Donc, pour résoudre m en utilisant m = (y2 - y1) / (X2 - X1), nous aurions m = (y2 - y1) / (4 - 4). Quelles que soient les deux valeurs y, vous diviserez toujours par 0.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
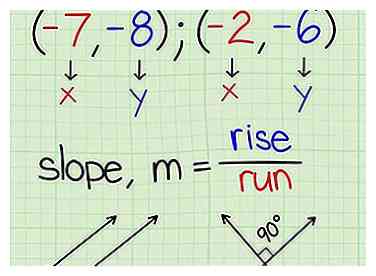 1 Voir si on vous donne 2 points ou 1 point et la pente. Si on vous donne 1 point sur la ligne et sa pente, vous pouvez continuer jusqu'à la Finir avec la formule Point-Slope méthode. Sinon, vous devrez utiliser les deux points donnés pour trouver la pente de la ligne.
1 Voir si on vous donne 2 points ou 1 point et la pente. Si on vous donne 1 point sur la ligne et sa pente, vous pouvez continuer jusqu'à la Finir avec la formule Point-Slope méthode. Sinon, vous devrez utiliser les deux points donnés pour trouver la pente de la ligne.  2 Utilisez toute autre information pour obtenir des points sur la ligne. Certains problèmes nécessitent une interprétation des informations sur la ligne pour obtenir un point sur la ligne. Par exemple, si on vous dit que la ligne traverse le origine, Tu le sais (0, 0) est un point sur la ligne!
2 Utilisez toute autre information pour obtenir des points sur la ligne. Certains problèmes nécessitent une interprétation des informations sur la ligne pour obtenir un point sur la ligne. Par exemple, si on vous dit que la ligne traverse le origine, Tu le sais (0, 0) est un point sur la ligne! 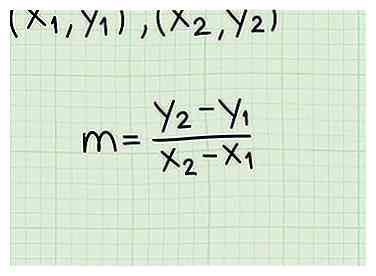 3 Calculez la pente de la ligne par les deux points. L'équation de la pente est m = (y2 - y1) / (X2 - X1). En branchant simplement vos points de coordonnées et en résolvant, vous connaissez maintenant la pente de l'équation.
3 Calculez la pente de la ligne par les deux points. L'équation de la pente est m = (y2 - y1) / (X2 - X1). En branchant simplement vos points de coordonnées et en résolvant, vous connaissez maintenant la pente de l'équation. 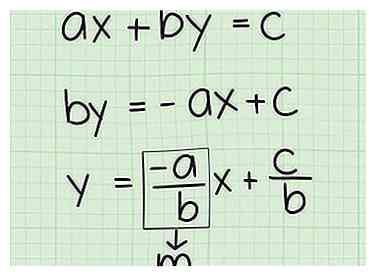 1 Utilisez la même pente si l'autre ligne est parallèle. Les lignes parallèles partagent la même pente, il suffit d'utiliser l'équation de cette ligne pour obtenir la pente de votre première ligne.
1 Utilisez la même pente si l'autre ligne est parallèle. Les lignes parallèles partagent la même pente, il suffit d'utiliser l'équation de cette ligne pour obtenir la pente de votre première ligne. 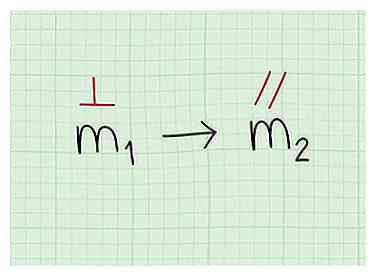 2 Trouvez la pente d'une ligne perpendiculaire. Souvent, les questions vous donneront un perpendiculaire ligne à la ligne que vous voulez une équation pour. Ici, vous utiliserez les mêmes concepts que précédemment pour déterminer la pente de la ligne perpendiculaire.
2 Trouvez la pente d'une ligne perpendiculaire. Souvent, les questions vous donneront un perpendiculaire ligne à la ligne que vous voulez une équation pour. Ici, vous utiliserez les mêmes concepts que précédemment pour déterminer la pente de la ligne perpendiculaire. 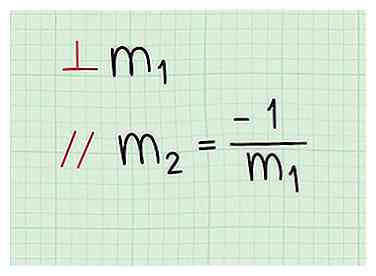 3 Utilisez l'inverse inverse de la pente de la ligne perpendiculaire. Toute ligne perpendiculaire à une autre ligne a une pente qui est la réciproque négative de l'autre ligne. Cela signifie que si la pente d'une ligne est 2, la pente d'une ligne perpendiculaire sera -1/2.
3 Utilisez l'inverse inverse de la pente de la ligne perpendiculaire. Toute ligne perpendiculaire à une autre ligne a une pente qui est la réciproque négative de l'autre ligne. Cela signifie que si la pente d'une ligne est 2, la pente d'une ligne perpendiculaire sera -1/2. 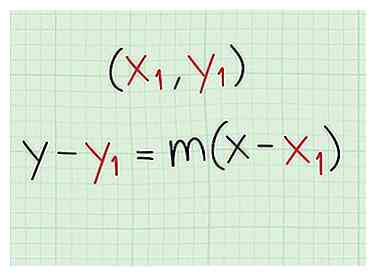 1 Utilisez le formule de pente ponctuelle pour trouver l'équation. Peu importe comment vous êtes arrivé, vous devriez avoir 1 point sur la ligne et la pente de la ligne. La formule à utiliser est y - y1 = m (x - x1). En utilisant la pente m vous venez de calculer et l'une des coordonnées données sur la ligne, branchez les chiffres dans l'équation.
1 Utilisez le formule de pente ponctuelle pour trouver l'équation. Peu importe comment vous êtes arrivé, vous devriez avoir 1 point sur la ligne et la pente de la ligne. La formule à utiliser est y - y1 = m (x - x1). En utilisant la pente m vous venez de calculer et l'une des coordonnées données sur la ligne, branchez les chiffres dans l'équation. 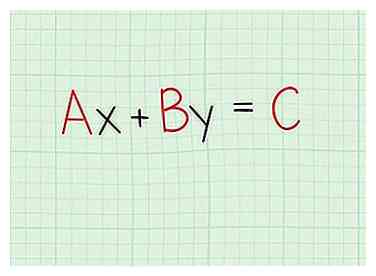 2 Réduire pour formater dans la réponse finale. Certains enseignants recherchent forme standard lequel est Axe + Par = C, où UNE, B, et C sont des coefficients numériques. D'autres voudront Forme d'interception de pente lequel est y = mx + b où m est la pente et b est le intercepter (où la ligne traverse l'axe des y).
2 Réduire pour formater dans la réponse finale. Certains enseignants recherchent forme standard lequel est Axe + Par = C, où UNE, B, et C sont des coefficients numériques. D'autres voudront Forme d'interception de pente lequel est y = mx + b où m est la pente et b est le intercepter (où la ligne traverse l'axe des y).  1 Prenez une pente de 0 comme bon signe. Si vous avez découvert que la pente est nulle, votre ligne est horizontale! L'équation pour toute ligne avec une pente de 0 est simplement y = b où b est l'endroit où la ligne traverse le axe y.
1 Prenez une pente de 0 comme bon signe. Si vous avez découvert que la pente est nulle, votre ligne est horizontale! L'équation pour toute ligne avec une pente de 0 est simplement y = b où b est l'endroit où la ligne traverse le axe y. 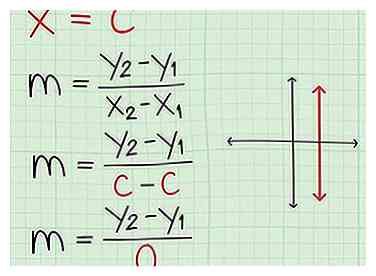 2 Expliquez que la ligne est verticale sinon. Les lignes verticales sont essentiellement le cas contraire. L'équation sera simplement x = c où c est le x-intercepter. Quand une ligne monte directement, elle aura un indéfini pente. C'est parce que quand vous résolvez pour m en utilisant 2 points de ces lignes, vous finirez par diviser par 0.
2 Expliquez que la ligne est verticale sinon. Les lignes verticales sont essentiellement le cas contraire. L'équation sera simplement x = c où c est le x-intercepter. Quand une ligne monte directement, elle aura un indéfini pente. C'est parce que quand vous résolvez pour m en utilisant 2 points de ces lignes, vous finirez par diviser par 0.