Les équations graphiques sont un processus beaucoup plus simple que la plupart des gens réalisent. Vous n'avez pas besoin d'être un génie des mathématiques ou un étudiant droit pour apprendre les bases de la représentation graphique sans utiliser de calculatrice. Apprenez quelques-unes de ces méthodes pour représenter graphiquement les équations linéaires, quadratiques, d'inégalité et de valeur absolue.
Méthode One of Six:
Représentation graphique des équations linéaires
-
 1 Utilisez la formule y = mx + b. Pour représenter graphiquement une équation linéaire, il suffit de la substituer dans les variables de cette formule.
1 Utilisez la formule y = mx + b. Pour représenter graphiquement une équation linéaire, il suffit de la substituer dans les variables de cette formule. - Dans la formule, vous devrez résoudre pour (x, y).
- La variable m = pente. La pente est également notée comme montée au-dessus de la course, ou le nombre de points que vous parcourez de haut en bas.
- Dans la formule, b = ordonnée à l'origine. C'est l'endroit sur votre graphique où la ligne se croise sur l'axe des y.
-
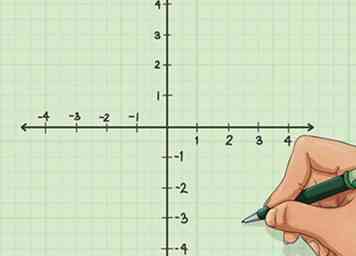 2 Dessine ton graphique. La représentation graphique d'une équation linéaire est la plus simple, car vous n'avez pas à calculer de nombres avant de créer des graphiques. Dessinez simplement votre plan de coordonnées cartésien.
2 Dessine ton graphique. La représentation graphique d'une équation linéaire est la plus simple, car vous n'avez pas à calculer de nombres avant de créer des graphiques. Dessinez simplement votre plan de coordonnées cartésien. -
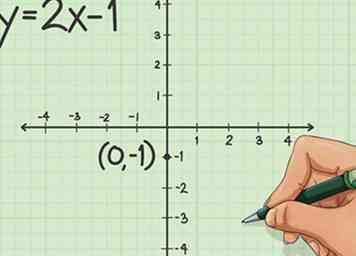 3 Trouvez l'ordonnée à l'origine (b) sur votre graphique. Si nous utilisons l'exemple de y = 2x-1, nous pouvons voir que «-1» est au point de l'équation où vous trouveriez «b». Cela fait '-1' l'ordonnée à l'origine.
3 Trouvez l'ordonnée à l'origine (b) sur votre graphique. Si nous utilisons l'exemple de y = 2x-1, nous pouvons voir que «-1» est au point de l'équation où vous trouveriez «b». Cela fait '-1' l'ordonnée à l'origine. - L'ordonnée à l'origine est toujours représentée avec x = 0. Par conséquent, les coordonnées d'interception y sont (0, -1).
- Placez un point sur votre graphique là où l'ordonnée à l'origine devrait être.
-
 4 Trouvez la pente. Dans l'exemple de y = 2x-1, la pente est le nombre où "m" serait trouvé. Cela signifie que selon notre exemple, la pente est «2». La pente, cependant, est la montée en puissance, il faut donc que la pente soit une fraction. Parce que "2" est un nombre entier et une fraction, il s'agit simplement de "2/1".
4 Trouvez la pente. Dans l'exemple de y = 2x-1, la pente est le nombre où "m" serait trouvé. Cela signifie que selon notre exemple, la pente est «2». La pente, cependant, est la montée en puissance, il faut donc que la pente soit une fraction. Parce que "2" est un nombre entier et une fraction, il s'agit simplement de "2/1". - Pour représenter graphiquement la pente, commencez à l'ordonnée à l'origine. L'augmentation (nombre d'espaces vers le haut) est le numérateur de la fraction, tandis que la course (nombre d'espaces sur le côté) est le dénominateur de la fraction.
- Dans notre exemple, nous allons représenter graphiquement la pente en commençant à -1, puis en remontant 2 et vers la droite 1.
- Une augmentation positive signifie que vous allez monter sur l'axe des y, alors qu'une augmentation négative signifie que vous allez descendre. Une course positive signifie que vous vous déplacerez à droite de l'axe des x, tandis qu'une course négative signifie que vous vous déplacerez à gauche de l'axe des x.
- Vous pouvez marquer autant de coordonnées que vous le souhaitez en utilisant la pente, mais vous devez en marquer au moins une.
-
 5 Dessine ta ligne Une fois que vous avez marqué au moins une autre coordonnée en utilisant la pente, vous pouvez la connecter à votre coordonnée d'interception y pour former une ligne. Étendre la ligne aux bords du graphique, et ajouter des points de flèche aux extrémités pour montrer qu'elle se poursuit à l'infini.[1]
5 Dessine ta ligne Une fois que vous avez marqué au moins une autre coordonnée en utilisant la pente, vous pouvez la connecter à votre coordonnée d'interception y pour former une ligne. Étendre la ligne aux bords du graphique, et ajouter des points de flèche aux extrémités pour montrer qu'elle se poursuit à l'infini.[1]
Méthode deux sur six:
Représenter les inégalités à variable unique
-
 1 Tracez une droite numérique. Étant donné que les inégalités à variable unique ne se produisent que sur un axe, vous ne devez pas utiliser de coordonnées cartésiennes. Au lieu de cela, dessinez une ligne de chiffres simple.
1 Tracez une droite numérique. Étant donné que les inégalités à variable unique ne se produisent que sur un axe, vous ne devez pas utiliser de coordonnées cartésiennes. Au lieu de cela, dessinez une ligne de chiffres simple. -
 2 Représentez graphiquement votre inégalité. Ce sont assez simples, car ils n'ont qu'une seule coordonnée. On vous donnera une inégalité telle que x <1 au graphique. Pour ce faire, trouvez d'abord «1» sur votre droite numérique.
2 Représentez graphiquement votre inégalité. Ce sont assez simples, car ils n'ont qu'une seule coordonnée. On vous donnera une inégalité telle que x <1 au graphique. Pour ce faire, trouvez d'abord «1» sur votre droite numérique. - Si vous recevez un symbole «supérieur à», qui est soit>, soit <, dessinez un cercle ouvert autour du nombre.
- Si vous recevez un symbole «supérieur ou égal à», soit> ou <, remplissez le cercle autour de votre point.
-
 3 Dessine ta ligne En utilisant le point que vous venez de créer, suivez le symbole d'inégalité pour tracer une ligne représentant l'inégalité. Si c'est plus grand que le point, alors la ligne ira à droite. Si c'est moins que le point, alors la ligne sera dessinée à gauche. Ajoutez une flèche à la fin pour montrer que la ligne continue et n'est pas un segment.
3 Dessine ta ligne En utilisant le point que vous venez de créer, suivez le symbole d'inégalité pour tracer une ligne représentant l'inégalité. Si c'est plus grand que le point, alors la ligne ira à droite. Si c'est moins que le point, alors la ligne sera dessinée à gauche. Ajoutez une flèche à la fin pour montrer que la ligne continue et n'est pas un segment. -
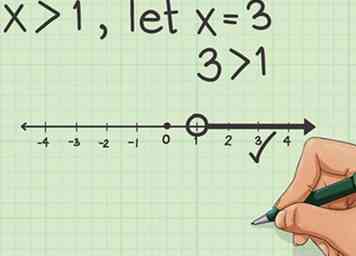 4 Vérifie ta réponse. Remplacez par un nombre quelconque égal à «x» et marquez-le sur votre droite numérique. Si ce nombre se trouve sur la ligne que vous avez dessinée, votre graphique est exact.
4 Vérifie ta réponse. Remplacez par un nombre quelconque égal à «x» et marquez-le sur votre droite numérique. Si ce nombre se trouve sur la ligne que vous avez dessinée, votre graphique est exact.
Méthode trois sur six:
Inégalités linéaires graphiques
-
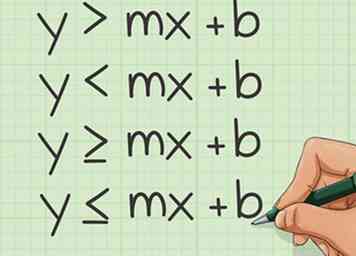 1 Utilisez le formulaire d'interception de pente. Ceci est la même formule utilisée pour représenter graphiquement les équations linéaires régulières, mais au lieu d'utiliser un signe '=', vous recevrez un signe d'inégalité. Le signe d'inégalité sera soit <,>, <ou>.
1 Utilisez le formulaire d'interception de pente. Ceci est la même formule utilisée pour représenter graphiquement les équations linéaires régulières, mais au lieu d'utiliser un signe '=', vous recevrez un signe d'inégalité. Le signe d'inégalité sera soit <,>, <ou>. - La forme d'interception de la pente est y = mx + b, où m = pente et b = ordonnée à l'origine.
- Avoir une inégalité présente signifie qu'il existe plusieurs solutions.
-
 2 Graphique l'inégalité. Trouvez l'ordonnée à l'origine et la pente pour marquer vos coordonnées. Si nous utilisons l'exemple de y> 1 / 2x + 2, alors l'ordonnée à l'origine est '1'. La pente est de ½, ce qui signifie que vous montez d’un point et que vous montez aux deux points de droite.
2 Graphique l'inégalité. Trouvez l'ordonnée à l'origine et la pente pour marquer vos coordonnées. Si nous utilisons l'exemple de y> 1 / 2x + 2, alors l'ordonnée à l'origine est '1'. La pente est de ½, ce qui signifie que vous montez d’un point et que vous montez aux deux points de droite. -
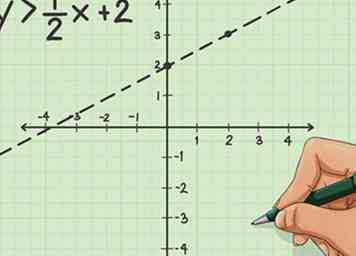 3 Dessine ta ligne Avant de le dessiner, vérifiez le symbole d'inégalité utilisé. S'il s'agit d'un symbole «supérieur à», votre ligne doit être tiretée. S'il s'agit d'un symbole «supérieur ou égal à», votre ligne doit être pleine.
3 Dessine ta ligne Avant de le dessiner, vérifiez le symbole d'inégalité utilisé. S'il s'agit d'un symbole «supérieur à», votre ligne doit être tiretée. S'il s'agit d'un symbole «supérieur ou égal à», votre ligne doit être pleine. -
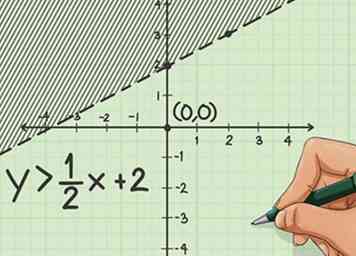 4 Ombrez votre graphique. Comme il existe plusieurs solutions à une inégalité, vous devez afficher toutes les solutions possibles sur votre graphique. Cela signifie que vous allez ombrer tout votre graphique au-dessus ou au-dessous de votre ligne.
4 Ombrez votre graphique. Comme il existe plusieurs solutions à une inégalité, vous devez afficher toutes les solutions possibles sur votre graphique. Cela signifie que vous allez ombrer tout votre graphique au-dessus ou au-dessous de votre ligne. - Choisissez une coordonnée - l'origine à (0,0) est souvent la plus facile. Assurez-vous de noter si cette coordonnée est au-dessus ou au-dessous de la ligne que vous avez dessinée.
- Remplacez ces coordonnées dans votre inégalité. Suivant notre exemple, ce serait 0> 1/2 (0) +1. Résoudre cette inégalité.
- Si la paire de coordonnées est un point au-dessus de votre ligne et que la réponse est vraie, vous devriez alors faire de l'ombre au-dessus de la ligne. Si la réponse à l'inégalité est fausse, alors vous seriez en-dessous de la ligne. Si les coordonnées se trouvent en dessous de votre ligne et que la réponse est vraie, vous faites de l'ombre en dessous de votre ligne. Si votre réponse est fausse, alors passez au-dessus de notre ligne.
- Dans notre exemple, (0,0) est en dessous de notre ligne et crée une fausse solution lorsqu'il est substitué à l'inégalité. Cela signifie que nous ombrons le reste du graphique au-dessus de la ligne.[2]
Méthode quatre sur six:
Équations quadratiques graphiques
-
 1 Examinez votre formule. Une équation quadratique signifie que vous avez au moins une variable au carré. Il sera typiquement écrit dans la formule y = ax (carré) + bx + c.
1 Examinez votre formule. Une équation quadratique signifie que vous avez au moins une variable au carré. Il sera typiquement écrit dans la formule y = ax (carré) + bx + c. - Représenter graphiquement une équation quadratique vous donnera une parabole, qui est une courbe en forme de «U».
- Vous aurez besoin de trouver au moins trois points pour le représenter graphiquement, en commençant par le sommet qui est le point le plus au centre.
-
 2 Trouvez 'a, "b,' et 'c'. Si nous utilisons l'exemple y = x (au carré) + 2x + 1, alors a = 1, b = 2 et c = 1. Chaque lettre correspond au nombre précédant directement la variable située à côté dans l'équation. S'il n'y a pas de nombre avant «x» dans l'équation, la variable est égale à «1» car il est supposé qu'il y a 1x.
2 Trouvez 'a, "b,' et 'c'. Si nous utilisons l'exemple y = x (au carré) + 2x + 1, alors a = 1, b = 2 et c = 1. Chaque lettre correspond au nombre précédant directement la variable située à côté dans l'équation. S'il n'y a pas de nombre avant «x» dans l'équation, la variable est égale à «1» car il est supposé qu'il y a 1x. -
 3 Trouvez le sommet. Pour trouver le sommet, le point au milieu de la parabole, utilisez la formule -b / 2a. Dans notre exemple, cette équation passerait à -2/2 (1), ce qui équivaut à -1.
3 Trouvez le sommet. Pour trouver le sommet, le point au milieu de la parabole, utilisez la formule -b / 2a. Dans notre exemple, cette équation passerait à -2/2 (1), ce qui équivaut à -1. -
 4 Faire une table. Vous connaissez maintenant le sommet, -1, qui est un point sur l'axe des x. Cependant, il ne s'agit que d'un point de la coordonnée de sommet. Pour trouver la coordonnée y correspondante ainsi que deux autres points sur votre parabole, vous devrez créer un tableau.
4 Faire une table. Vous connaissez maintenant le sommet, -1, qui est un point sur l'axe des x. Cependant, il ne s'agit que d'un point de la coordonnée de sommet. Pour trouver la coordonnée y correspondante ainsi que deux autres points sur votre parabole, vous devrez créer un tableau. -
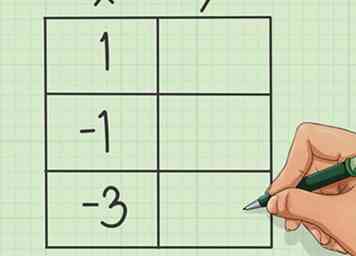 5 Créez un tableau comportant trois lignes et deux colonnes.
5 Créez un tableau comportant trois lignes et deux colonnes. - Placez la coordonnée x pour le sommet dans la colonne centrale supérieure.
- Choisissez deux autres coordonnées x, un nombre égal dans chaque direction (positif et négatif) à partir du sommet. Par exemple, nous pourrions monter de deux à deux, en remplissant les deux autres espaces vides «-3» et «1».
- Vous pouvez choisir n'importe quel nombre que vous souhaitez remplir dans la rangée supérieure du tableau, à condition qu'il s'agisse de nombres entiers et de la même distance du sommet.
- Si vous voulez avoir un graphique plus clair, vous pouvez trouver cinq coordonnées au lieu de trois. Faire ceci est le même processus que ci-dessus, mais donnez à votre table cinq colonnes au lieu de trois.
-
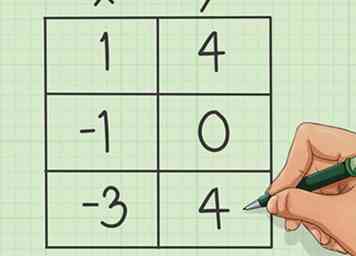 6 Utilisez votre tableau et votre formule pour résoudre les coordonnées y. Un à la fois, prenez les numéros que vous avez sélectionnés pour représenter les coordonnées x de votre tableau et insérez-les dans l'équation d'origine. Résoudre pour 'y'.
6 Utilisez votre tableau et votre formule pour résoudre les coordonnées y. Un à la fois, prenez les numéros que vous avez sélectionnés pour représenter les coordonnées x de votre tableau et insérez-les dans l'équation d'origine. Résoudre pour 'y'. - Suivant notre exemple, nous pourrions utiliser notre coordonnée choisie de '-3' pour substituer la formule originale de y = x (carré) + 2x + 1. Cela passerait à y = -3 (au carré) +2 (3) +1, donnant une réponse de y = 4.
- Placez la nouvelle coordonnée y sous la coordonnée x que vous avez utilisée dans votre table.
- Résoudre les trois (ou cinq, si vous voulez plus) coordonnées de cette façon.
-
 7 Graphique les coordonnées. Maintenant que vous avez au moins trois paires de coordonnées complètes, marquez-les sur votre graphique. Dessine une connexion entre eux dans une parabole et tu as fini!
7 Graphique les coordonnées. Maintenant que vous avez au moins trois paires de coordonnées complètes, marquez-les sur votre graphique. Dessine une connexion entre eux dans une parabole et tu as fini!
Méthode cinq sur six:
Représenter graphiquement une inégalité quadratique
-
 1 Résoudre la formule quadratique. Une inégalité quadratique utilise la même formule que la formule quadratique mais utilisera plutôt un symbole d'inégalité. Par exemple, cela ressemblera à y
1 Résoudre la formule quadratique. Une inégalité quadratique utilise la même formule que la formule quadratique mais utilisera plutôt un symbole d'inégalité. Par exemple, cela ressemblera à y -
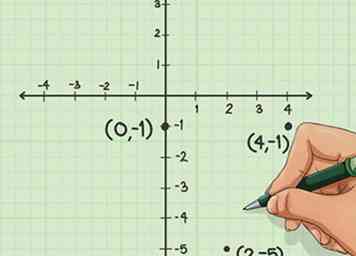 2 Marquez les coordonnées sur votre graphique. Bien que vous ayez suffisamment de points pour réaliser votre parabole complète, ne dessinez pas encore la forme.
2 Marquez les coordonnées sur votre graphique. Bien que vous ayez suffisamment de points pour réaliser votre parabole complète, ne dessinez pas encore la forme. -
 3 Connectez les points sur votre graphique. Comme vous tracez une inégalité quadratique, la ligne que vous tracez sera un peu différente.
3 Connectez les points sur votre graphique. Comme vous tracez une inégalité quadratique, la ligne que vous tracez sera un peu différente. - Si votre symbole d'inégalité était «supérieur à» ou «inférieur à» (> ou <), vous tracez une ligne en pointillés entre les coordonnées.
- Si votre symbole d'inégalité était «supérieur ou égal à» ou «inférieur ou égal à» (> ou <), la ligne que vous dessinez sera solide.
- Terminez vos lignes avec des points de flèche pour montrer que les solutions s'étendent au-delà de la plage de votre graphique.
-
 4 Ombrez le graphique. Pour afficher plusieurs solutions, ombrer la partie du graphique dans laquelle la solution peut être trouvée. Pour savoir quelle partie du graphique doit être ombrée, testez une paire de coordonnées dans votre formule. Un ensemble facile à utiliser est (0,0). Notez si ces coordonnées se trouvent ou non à l'intérieur de votre parabole.
4 Ombrez le graphique. Pour afficher plusieurs solutions, ombrer la partie du graphique dans laquelle la solution peut être trouvée. Pour savoir quelle partie du graphique doit être ombrée, testez une paire de coordonnées dans votre formule. Un ensemble facile à utiliser est (0,0). Notez si ces coordonnées se trouvent ou non à l'intérieur de votre parabole. - Résolvez l'inégalité avec les coordonnées que vous avez choisies. Si nous utilisons un exemple de y> x (carré) -4x-1 et substituons les coordonnées (0,0), alors il passera à 0> 0 (carré) -4 (0) -1.
- Si la solution à ce problème est vraie et que les coordonnées sont à l'intérieur de la parabole, ombre à l'intérieur de la parabole. Si la solution est fausse, faites de l'ombre à l'extérieur de la parabole.
- Si la solution à ce problème est vraie et que les coordonnées sont en dehors de la parabole, ombragez l'extérieur de la parabole. Si la solution est fausse, ombrer l'intérieur de la parabole.[3]
Méthode six sur six:
Représentation graphique d'une équation de valeur absolue
-
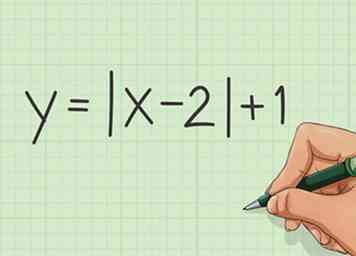 1 Examinez votre équation. L'équation de valeur absolue la plus élémentaire apparaîtra comme y = | x |. D'autres nombres ou variables peuvent cependant être impliqués.
1 Examinez votre équation. L'équation de valeur absolue la plus élémentaire apparaîtra comme y = | x |. D'autres nombres ou variables peuvent cependant être impliqués. -
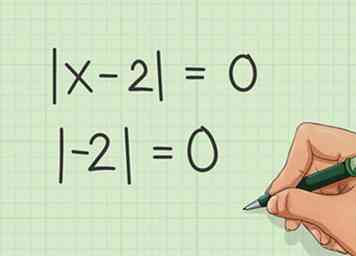 2 Rendre la valeur absolue égale à 0. Pour ce faire, faites tout dans les lignes de valeur absolue | | = 0. Si nous utilisons l'exemple y = | x-2 | +1, nous obtenons la valeur absolue en faisant | x-2 | = 0. La valeur absolue devient alors 2.
2 Rendre la valeur absolue égale à 0. Pour ce faire, faites tout dans les lignes de valeur absolue | | = 0. Si nous utilisons l'exemple y = | x-2 | +1, nous obtenons la valeur absolue en faisant | x-2 | = 0. La valeur absolue devient alors 2. - La valeur absolue est le nombre de points de | x | à "0" sur une droite numérique. Donc, la valeur absolue de | 2 | est 2 et la valeur absolue de | -2 | est aussi deux. En effet, dans les deux cas, «2» et «-2» sont à 2 pas de zéro sur la droite numérique.
- Vous pouvez avoir une équation de valeur absolue où «x» est seul. Dans ce cas, la valeur absolue est "0". Par exemple, y = | x | +3 change pour y = | 0 | +3, ce qui équivaut à '3'.
-
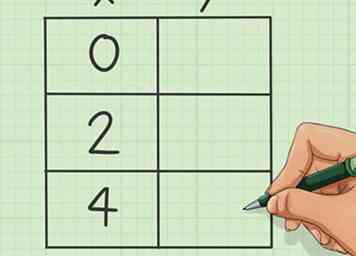 3 Faire une table. Vous voulez qu'il ait trois lignes et deux colonnes.
3 Faire une table. Vous voulez qu'il ait trois lignes et deux colonnes. - Placez la première coordonnée de valeur absolue dans la colonne centrale supérieure pour «X».
- Choisissez deux autres nombres à égale distance de votre coordonnée x dans chaque direction (positive et négative).Si | x | = 0, déplacez-vous d'un nombre égal d'espaces à partir de "0".
- Vous pouvez choisir n'importe quel nombre, bien que ceux qui sont proches de la coordonnée x soient les plus utiles. Ils doivent aussi être des nombres entiers.
-
 4 Résoudre l'inégalité. Vous devez trouver la coordonnée y qui est associée aux trois coordonnées x que vous avez. Pour ce faire, remplacez les valeurs de coordonnées x par l'inégalité et résolvez «y». Remplissez ces réponses sur votre table.
4 Résoudre l'inégalité. Vous devez trouver la coordonnée y qui est associée aux trois coordonnées x que vous avez. Pour ce faire, remplacez les valeurs de coordonnées x par l'inégalité et résolvez «y». Remplissez ces réponses sur votre table. -
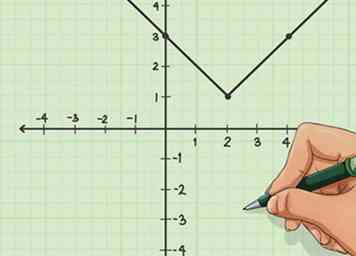 5 Graphique les points. Vous n'avez besoin que de trois points pour représenter graphiquement une équation de valeur absolue, mais vous pouvez en utiliser plus si vous le souhaitez. Une équation de valeur absolue formera toujours une forme de «V» sur votre graphique. Ajoutez des flèches aux extrémités pour indiquer que la ligne s'étend plus loin que le bord de votre graphique.[4]
5 Graphique les points. Vous n'avez besoin que de trois points pour représenter graphiquement une équation de valeur absolue, mais vous pouvez en utiliser plus si vous le souhaitez. Une équation de valeur absolue formera toujours une forme de «V» sur votre graphique. Ajoutez des flèches aux extrémités pour indiquer que la ligne s'étend plus loin que le bord de votre graphique.[4]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Utilisez la formule y = mx + b. Pour représenter graphiquement une équation linéaire, il suffit de la substituer dans les variables de cette formule.
1 Utilisez la formule y = mx + b. Pour représenter graphiquement une équation linéaire, il suffit de la substituer dans les variables de cette formule.  2 Dessine ton graphique. La représentation graphique d'une équation linéaire est la plus simple, car vous n'avez pas à calculer de nombres avant de créer des graphiques. Dessinez simplement votre plan de coordonnées cartésien.
2 Dessine ton graphique. La représentation graphique d'une équation linéaire est la plus simple, car vous n'avez pas à calculer de nombres avant de créer des graphiques. Dessinez simplement votre plan de coordonnées cartésien. 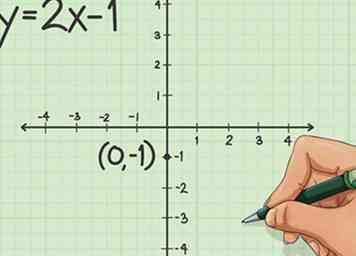 3 Trouvez l'ordonnée à l'origine (b) sur votre graphique. Si nous utilisons l'exemple de y = 2x-1, nous pouvons voir que «-1» est au point de l'équation où vous trouveriez «b». Cela fait '-1' l'ordonnée à l'origine.
3 Trouvez l'ordonnée à l'origine (b) sur votre graphique. Si nous utilisons l'exemple de y = 2x-1, nous pouvons voir que «-1» est au point de l'équation où vous trouveriez «b». Cela fait '-1' l'ordonnée à l'origine.  4 Trouvez la pente. Dans l'exemple de y = 2x-1, la pente est le nombre où "m" serait trouvé. Cela signifie que selon notre exemple, la pente est «2». La pente, cependant, est la montée en puissance, il faut donc que la pente soit une fraction. Parce que "2" est un nombre entier et une fraction, il s'agit simplement de "2/1".
4 Trouvez la pente. Dans l'exemple de y = 2x-1, la pente est le nombre où "m" serait trouvé. Cela signifie que selon notre exemple, la pente est «2». La pente, cependant, est la montée en puissance, il faut donc que la pente soit une fraction. Parce que "2" est un nombre entier et une fraction, il s'agit simplement de "2/1".  5 Dessine ta ligne Une fois que vous avez marqué au moins une autre coordonnée en utilisant la pente, vous pouvez la connecter à votre coordonnée d'interception y pour former une ligne. Étendre la ligne aux bords du graphique, et ajouter des points de flèche aux extrémités pour montrer qu'elle se poursuit à l'infini.[1]
5 Dessine ta ligne Une fois que vous avez marqué au moins une autre coordonnée en utilisant la pente, vous pouvez la connecter à votre coordonnée d'interception y pour former une ligne. Étendre la ligne aux bords du graphique, et ajouter des points de flèche aux extrémités pour montrer qu'elle se poursuit à l'infini.[1]  1 Tracez une droite numérique. Étant donné que les inégalités à variable unique ne se produisent que sur un axe, vous ne devez pas utiliser de coordonnées cartésiennes. Au lieu de cela, dessinez une ligne de chiffres simple.
1 Tracez une droite numérique. Étant donné que les inégalités à variable unique ne se produisent que sur un axe, vous ne devez pas utiliser de coordonnées cartésiennes. Au lieu de cela, dessinez une ligne de chiffres simple.  2 Représentez graphiquement votre inégalité. Ce sont assez simples, car ils n'ont qu'une seule coordonnée. On vous donnera une inégalité telle que x <1 au graphique. Pour ce faire, trouvez d'abord «1» sur votre droite numérique.
2 Représentez graphiquement votre inégalité. Ce sont assez simples, car ils n'ont qu'une seule coordonnée. On vous donnera une inégalité telle que x <1 au graphique. Pour ce faire, trouvez d'abord «1» sur votre droite numérique.  3 Dessine ta ligne En utilisant le point que vous venez de créer, suivez le symbole d'inégalité pour tracer une ligne représentant l'inégalité. Si c'est plus grand que le point, alors la ligne ira à droite. Si c'est moins que le point, alors la ligne sera dessinée à gauche. Ajoutez une flèche à la fin pour montrer que la ligne continue et n'est pas un segment.
3 Dessine ta ligne En utilisant le point que vous venez de créer, suivez le symbole d'inégalité pour tracer une ligne représentant l'inégalité. Si c'est plus grand que le point, alors la ligne ira à droite. Si c'est moins que le point, alors la ligne sera dessinée à gauche. Ajoutez une flèche à la fin pour montrer que la ligne continue et n'est pas un segment. 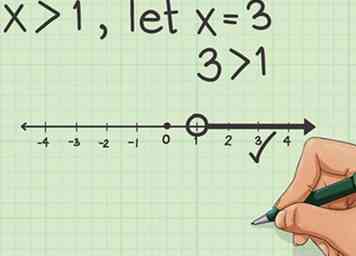 4 Vérifie ta réponse. Remplacez par un nombre quelconque égal à «x» et marquez-le sur votre droite numérique. Si ce nombre se trouve sur la ligne que vous avez dessinée, votre graphique est exact.
4 Vérifie ta réponse. Remplacez par un nombre quelconque égal à «x» et marquez-le sur votre droite numérique. Si ce nombre se trouve sur la ligne que vous avez dessinée, votre graphique est exact. 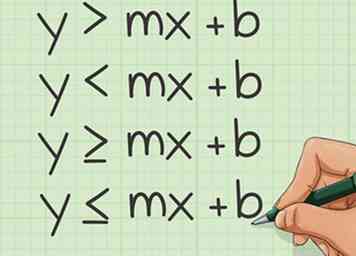 1 Utilisez le formulaire d'interception de pente. Ceci est la même formule utilisée pour représenter graphiquement les équations linéaires régulières, mais au lieu d'utiliser un signe '=', vous recevrez un signe d'inégalité. Le signe d'inégalité sera soit <,>, <ou>.
1 Utilisez le formulaire d'interception de pente. Ceci est la même formule utilisée pour représenter graphiquement les équations linéaires régulières, mais au lieu d'utiliser un signe '=', vous recevrez un signe d'inégalité. Le signe d'inégalité sera soit <,>, <ou>.  2 Graphique l'inégalité. Trouvez l'ordonnée à l'origine et la pente pour marquer vos coordonnées. Si nous utilisons l'exemple de y> 1 / 2x + 2, alors l'ordonnée à l'origine est '1'. La pente est de ½, ce qui signifie que vous montez d’un point et que vous montez aux deux points de droite.
2 Graphique l'inégalité. Trouvez l'ordonnée à l'origine et la pente pour marquer vos coordonnées. Si nous utilisons l'exemple de y> 1 / 2x + 2, alors l'ordonnée à l'origine est '1'. La pente est de ½, ce qui signifie que vous montez d’un point et que vous montez aux deux points de droite.  3 Dessine ta ligne Avant de le dessiner, vérifiez le symbole d'inégalité utilisé. S'il s'agit d'un symbole «supérieur à», votre ligne doit être tiretée. S'il s'agit d'un symbole «supérieur ou égal à», votre ligne doit être pleine.
3 Dessine ta ligne Avant de le dessiner, vérifiez le symbole d'inégalité utilisé. S'il s'agit d'un symbole «supérieur à», votre ligne doit être tiretée. S'il s'agit d'un symbole «supérieur ou égal à», votre ligne doit être pleine.  4 Ombrez votre graphique. Comme il existe plusieurs solutions à une inégalité, vous devez afficher toutes les solutions possibles sur votre graphique. Cela signifie que vous allez ombrer tout votre graphique au-dessus ou au-dessous de votre ligne.
4 Ombrez votre graphique. Comme il existe plusieurs solutions à une inégalité, vous devez afficher toutes les solutions possibles sur votre graphique. Cela signifie que vous allez ombrer tout votre graphique au-dessus ou au-dessous de votre ligne.  1 Examinez votre formule. Une équation quadratique signifie que vous avez au moins une variable au carré. Il sera typiquement écrit dans la formule y = ax (carré) + bx + c.
1 Examinez votre formule. Une équation quadratique signifie que vous avez au moins une variable au carré. Il sera typiquement écrit dans la formule y = ax (carré) + bx + c.  2 Trouvez 'a, "b,' et 'c'. Si nous utilisons l'exemple y = x (au carré) + 2x + 1, alors a = 1, b = 2 et c = 1. Chaque lettre correspond au nombre précédant directement la variable située à côté dans l'équation. S'il n'y a pas de nombre avant «x» dans l'équation, la variable est égale à «1» car il est supposé qu'il y a 1x.
2 Trouvez 'a, "b,' et 'c'. Si nous utilisons l'exemple y = x (au carré) + 2x + 1, alors a = 1, b = 2 et c = 1. Chaque lettre correspond au nombre précédant directement la variable située à côté dans l'équation. S'il n'y a pas de nombre avant «x» dans l'équation, la variable est égale à «1» car il est supposé qu'il y a 1x.  3 Trouvez le sommet. Pour trouver le sommet, le point au milieu de la parabole, utilisez la formule -b / 2a. Dans notre exemple, cette équation passerait à -2/2 (1), ce qui équivaut à -1.
3 Trouvez le sommet. Pour trouver le sommet, le point au milieu de la parabole, utilisez la formule -b / 2a. Dans notre exemple, cette équation passerait à -2/2 (1), ce qui équivaut à -1.  4 Faire une table. Vous connaissez maintenant le sommet, -1, qui est un point sur l'axe des x. Cependant, il ne s'agit que d'un point de la coordonnée de sommet. Pour trouver la coordonnée y correspondante ainsi que deux autres points sur votre parabole, vous devrez créer un tableau.
4 Faire une table. Vous connaissez maintenant le sommet, -1, qui est un point sur l'axe des x. Cependant, il ne s'agit que d'un point de la coordonnée de sommet. Pour trouver la coordonnée y correspondante ainsi que deux autres points sur votre parabole, vous devrez créer un tableau.  5 Créez un tableau comportant trois lignes et deux colonnes.
5 Créez un tableau comportant trois lignes et deux colonnes.  6 Utilisez votre tableau et votre formule pour résoudre les coordonnées y. Un à la fois, prenez les numéros que vous avez sélectionnés pour représenter les coordonnées x de votre tableau et insérez-les dans l'équation d'origine. Résoudre pour 'y'.
6 Utilisez votre tableau et votre formule pour résoudre les coordonnées y. Un à la fois, prenez les numéros que vous avez sélectionnés pour représenter les coordonnées x de votre tableau et insérez-les dans l'équation d'origine. Résoudre pour 'y'.  7 Graphique les coordonnées. Maintenant que vous avez au moins trois paires de coordonnées complètes, marquez-les sur votre graphique. Dessine une connexion entre eux dans une parabole et tu as fini!
7 Graphique les coordonnées. Maintenant que vous avez au moins trois paires de coordonnées complètes, marquez-les sur votre graphique. Dessine une connexion entre eux dans une parabole et tu as fini!  1 Résoudre la formule quadratique. Une inégalité quadratique utilise la même formule que la formule quadratique mais utilisera plutôt un symbole d'inégalité. Par exemple, cela ressemblera à y
1 Résoudre la formule quadratique. Une inégalité quadratique utilise la même formule que la formule quadratique mais utilisera plutôt un symbole d'inégalité. Par exemple, cela ressemblera à y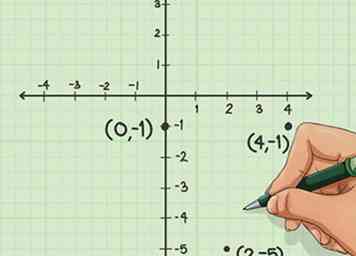 2 Marquez les coordonnées sur votre graphique. Bien que vous ayez suffisamment de points pour réaliser votre parabole complète, ne dessinez pas encore la forme.
2 Marquez les coordonnées sur votre graphique. Bien que vous ayez suffisamment de points pour réaliser votre parabole complète, ne dessinez pas encore la forme.  3 Connectez les points sur votre graphique. Comme vous tracez une inégalité quadratique, la ligne que vous tracez sera un peu différente.
3 Connectez les points sur votre graphique. Comme vous tracez une inégalité quadratique, la ligne que vous tracez sera un peu différente.  4 Ombrez le graphique. Pour afficher plusieurs solutions, ombrer la partie du graphique dans laquelle la solution peut être trouvée. Pour savoir quelle partie du graphique doit être ombrée, testez une paire de coordonnées dans votre formule. Un ensemble facile à utiliser est (0,0). Notez si ces coordonnées se trouvent ou non à l'intérieur de votre parabole.
4 Ombrez le graphique. Pour afficher plusieurs solutions, ombrer la partie du graphique dans laquelle la solution peut être trouvée. Pour savoir quelle partie du graphique doit être ombrée, testez une paire de coordonnées dans votre formule. Un ensemble facile à utiliser est (0,0). Notez si ces coordonnées se trouvent ou non à l'intérieur de votre parabole. 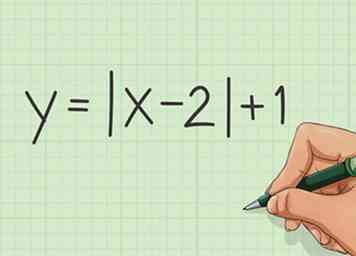 1 Examinez votre équation. L'équation de valeur absolue la plus élémentaire apparaîtra comme y = | x |. D'autres nombres ou variables peuvent cependant être impliqués.
1 Examinez votre équation. L'équation de valeur absolue la plus élémentaire apparaîtra comme y = | x |. D'autres nombres ou variables peuvent cependant être impliqués. 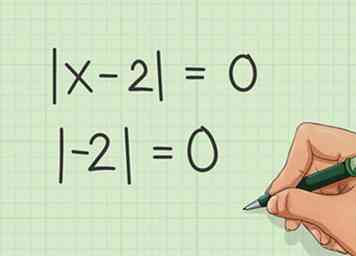 2 Rendre la valeur absolue égale à 0. Pour ce faire, faites tout dans les lignes de valeur absolue | | = 0. Si nous utilisons l'exemple y = | x-2 | +1, nous obtenons la valeur absolue en faisant | x-2 | = 0. La valeur absolue devient alors 2.
2 Rendre la valeur absolue égale à 0. Pour ce faire, faites tout dans les lignes de valeur absolue | | = 0. Si nous utilisons l'exemple y = | x-2 | +1, nous obtenons la valeur absolue en faisant | x-2 | = 0. La valeur absolue devient alors 2.  3 Faire une table. Vous voulez qu'il ait trois lignes et deux colonnes.
3 Faire une table. Vous voulez qu'il ait trois lignes et deux colonnes.  4 Résoudre l'inégalité. Vous devez trouver la coordonnée y qui est associée aux trois coordonnées x que vous avez. Pour ce faire, remplacez les valeurs de coordonnées x par l'inégalité et résolvez «y». Remplissez ces réponses sur votre table.
4 Résoudre l'inégalité. Vous devez trouver la coordonnée y qui est associée aux trois coordonnées x que vous avez. Pour ce faire, remplacez les valeurs de coordonnées x par l'inégalité et résolvez «y». Remplissez ces réponses sur votre table.  5 Graphique les points. Vous n'avez besoin que de trois points pour représenter graphiquement une équation de valeur absolue, mais vous pouvez en utiliser plus si vous le souhaitez. Une équation de valeur absolue formera toujours une forme de «V» sur votre graphique. Ajoutez des flèches aux extrémités pour indiquer que la ligne s'étend plus loin que le bord de votre graphique.[4]
5 Graphique les points. Vous n'avez besoin que de trois points pour représenter graphiquement une équation de valeur absolue, mais vous pouvez en utiliser plus si vous le souhaitez. Une équation de valeur absolue formera toujours une forme de «V» sur votre graphique. Ajoutez des flèches aux extrémités pour indiquer que la ligne s'étend plus loin que le bord de votre graphique.[4]