En mathématiques, un vecteur est un objet dont la longueur est définie, appelée magnitude et direction. Puisque les vecteurs ne sont pas les mêmes que les lignes ou les formes standard, vous devrez utiliser des formules spéciales pour trouver des angles entre eux.
Première partie de deux:
Trouver l'angle entre deux vecteurs
-
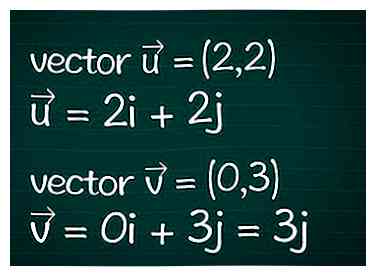 1 Identifier les vecteurs. Notez toutes les informations que vous avez concernant les deux vecteurs. Nous supposerons que vous avez uniquement la définition du vecteur en termes de coordonnées dimensionnelles (également appelées composants). Si vous connaissez déjà la longueur d'un vecteur (son ampleur), vous pourrez ignorer certaines des étapes ci-dessous.
1 Identifier les vecteurs. Notez toutes les informations que vous avez concernant les deux vecteurs. Nous supposerons que vous avez uniquement la définition du vecteur en termes de coordonnées dimensionnelles (également appelées composants). Si vous connaissez déjà la longueur d'un vecteur (son ampleur), vous pourrez ignorer certaines des étapes ci-dessous. - Exemple: le vecteur bidimensionnel = (2,2) Vecteur = (0,3). Ceux-ci peuvent également être écrits comme = 2je + 2j et = 0je + 3j = 3j.
- Alors que notre exemple utilise des vecteurs à deux dimensions, les instructions ci-dessous couvrent les vecteurs avec un nombre quelconque de composants.
-
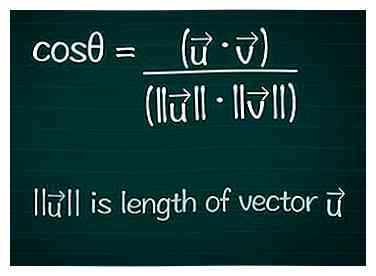 2 Notez la formule du cosinus. Pour trouver l'angle θ entre deux vecteurs, commencez par la formule pour trouver le cosinus de cet angle. Vous pouvez en apprendre davantage sur cette formule ci-dessous, ou simplement la noter:[1]
2 Notez la formule du cosinus. Pour trouver l'angle θ entre deux vecteurs, commencez par la formule pour trouver le cosinus de cet angle. Vous pouvez en apprendre davantage sur cette formule ci-dessous, ou simplement la noter:[1] - cosθ = ( • ) / (|||| ||||)
- |||| signifie "la longueur du vecteur ."
- • est le produit scalaire (produit scalaire) des deux vecteurs, expliqué ci-dessous.
-
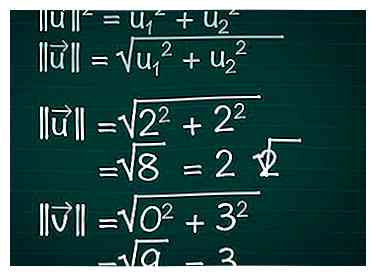 3 Calculez la longueur de chaque vecteur. Imaginez un triangle rectangle tiré du composant x du vecteur, de sa composante y et du vecteur lui-même. Le vecteur forme l'hypoténuse du triangle. Pour trouver sa longueur, nous utilisons le théorème de Pythagore. Il s'avère que cette formule est facilement étendue aux vecteurs avec un nombre quelconque de composants.
3 Calculez la longueur de chaque vecteur. Imaginez un triangle rectangle tiré du composant x du vecteur, de sa composante y et du vecteur lui-même. Le vecteur forme l'hypoténuse du triangle. Pour trouver sa longueur, nous utilisons le théorème de Pythagore. Il s'avère que cette formule est facilement étendue aux vecteurs avec un nombre quelconque de composants.
Calcul de la longueur de vecteur Exemple
||tu||2 = tu12 + tu22. Si un vecteur a plus de deux composants, continuez simplement à ajouter + u32 + tu42 +…
Par conséquent, pour un vecteur à deux dimensions, ||tu|| = √ (u12 + tu22).
Dans notre exemple, |||| = √(22 + 22) = √(8) = 2√2. |||| = √(02 + 32) = √(9) = 3.
-
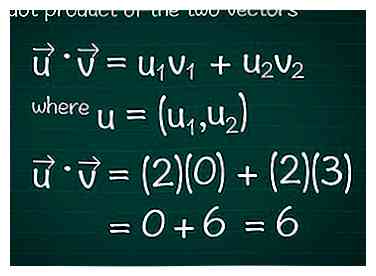 4 Calculez le produit scalaire des deux vecteurs. Vous avez probablement déjà appris cette méthode de multiplication de vecteurs, également appelée produit scalaire.[2]Pour calculer le produit scalaire en fonction des composants des vecteurs, multipliez les composants dans chaque direction, puis ajoutez tous les résultats. Pour les programmes graphiques, voir Astuces avant de continuer. Exemple de produit trouvé
4 Calculez le produit scalaire des deux vecteurs. Vous avez probablement déjà appris cette méthode de multiplication de vecteurs, également appelée produit scalaire.[2]Pour calculer le produit scalaire en fonction des composants des vecteurs, multipliez les composants dans chaque direction, puis ajoutez tous les résultats. Pour les programmes graphiques, voir Astuces avant de continuer. Exemple de produit trouvé
En termes mathématiques, • = tu1v1 + tu2v2, où u = (u1, tu2). Si votre vecteur a plus de deux composants, continuez simplement à ajouter + u3v3 + tu4v4…
Dans notre exemple, • = tu1v1 + tu2v2 = (2)(0) + (2)(3) = 0 + 6 = 6. Ceci est le produit scalaire du vecteur et .
-
 5 Branchez vos résultats dans la formule. Rappelez-vous, cosθ = ( • ) / (|||| || ||). Vous connaissez maintenant le produit scalaire et les longueurs de chaque vecteur. Entrez ces dans cette formule pour calculer le cosinus de l'angle. Recherche de cosinus avec des longueurs de produit et de vecteur
5 Branchez vos résultats dans la formule. Rappelez-vous, cosθ = ( • ) / (|||| || ||). Vous connaissez maintenant le produit scalaire et les longueurs de chaque vecteur. Entrez ces dans cette formule pour calculer le cosinus de l'angle. Recherche de cosinus avec des longueurs de produit et de vecteur
Dans notre exemple, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.
-
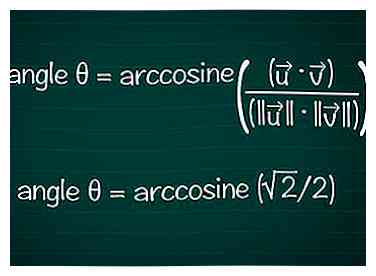 6 Trouvez l'angle basé sur le cosinus. Vous pouvez utiliser le arccos ou cos-1 fonction sur votre calculatrice pour trouver l'angle θ à partir d'une valeur cos θ connue. Pour certains résultats, vous pourrez peut-être déterminer l'angle en fonction du cercle unitaire. Trouver un angle avec Cosinus
6 Trouvez l'angle basé sur le cosinus. Vous pouvez utiliser le arccos ou cos-1 fonction sur votre calculatrice pour trouver l'angle θ à partir d'une valeur cos θ connue. Pour certains résultats, vous pourrez peut-être déterminer l'angle en fonction du cercle unitaire. Trouver un angle avec Cosinus
Dans notre exemple, cosθ = √2 / 2. Entrez "arccos (√2 / 2)" dans votre calculatrice pour obtenir l'angle. Sinon, trouvez l’angle θ sur le cercle unitaire où cosθ = √2 / 2. Ceci est vrai pour θ = π/4 ou 45º.
En somme, la formule finale est: angle θ = arccosine (( • ) / (|||| || ||))
Deuxième partie de deux:
Définir la formule d'angle
-
 1 Comprendre le but de cette formule. Cette formule n'a pas été dérivée des règles existantes. Au lieu de cela, il a été créé comme une définition du produit scalaire de deux vecteurs et de l'angle entre eux.[3] Cependant, cette décision n'était pas arbitraire.En revenant à la géométrie de base, nous pouvons voir pourquoi cette formule donne des définitions intuitives et utiles.
1 Comprendre le but de cette formule. Cette formule n'a pas été dérivée des règles existantes. Au lieu de cela, il a été créé comme une définition du produit scalaire de deux vecteurs et de l'angle entre eux.[3] Cependant, cette décision n'était pas arbitraire.En revenant à la géométrie de base, nous pouvons voir pourquoi cette formule donne des définitions intuitives et utiles. - Les exemples ci-dessous utilisent des vecteurs bidimensionnels, car ils sont les plus intuitifs à utiliser. Les vecteurs à trois composants ou plus ont des propriétés définies avec la formule générale très similaire.
-
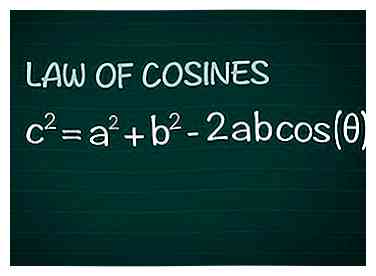 2 Passez en revue la loi des cosinus. Prenez un triangle ordinaire avec un angle θ entre les côtés a et b et le côté opposé c. La loi des cosinus stipule que c2 = a2 + b2 -2abcos(θ). Cela découle assez facilement de la géométrie de base.
2 Passez en revue la loi des cosinus. Prenez un triangle ordinaire avec un angle θ entre les côtés a et b et le côté opposé c. La loi des cosinus stipule que c2 = a2 + b2 -2abcos(θ). Cela découle assez facilement de la géométrie de base. -
 3 Connectez deux vecteurs pour former un triangle. Esquisser une paire de vecteurs 2D sur papier, vecteurs et , avec un angle θ entre eux. Dessinez un troisième vecteur entre eux pour former un triangle. En d'autres termes, dessiner un vecteur tel que + = . Ce vecteur = - .[4]
3 Connectez deux vecteurs pour former un triangle. Esquisser une paire de vecteurs 2D sur papier, vecteurs et , avec un angle θ entre eux. Dessinez un troisième vecteur entre eux pour former un triangle. En d'autres termes, dessiner un vecteur tel que + = . Ce vecteur = - .[4] -
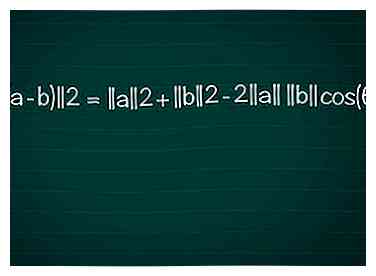 4 Écrivez la loi des cosinus pour ce triangle. Insérez la longueur de nos côtés "triangle vectoriel" dans la loi des cosinus:
4 Écrivez la loi des cosinus pour ce triangle. Insérez la longueur de nos côtés "triangle vectoriel" dans la loi des cosinus: - ||(un B)||2 = ||une||2 + ||b||2 - 2||une|| ||b||cos(θ)
-
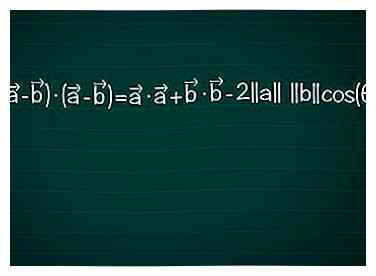 5 Ecrivez ceci en utilisant des produits scalaires. Rappelez-vous qu'un produit scalaire est le grossissement d'un vecteur projeté sur un autre. Le produit scalaire d'un vecteur avec lui-même ne nécessite aucune projection, car il n'y a pas de différence de direction.[5] Cela signifie que • = ||une||2. Utilisez ce fait pour réécrire l'équation:
5 Ecrivez ceci en utilisant des produits scalaires. Rappelez-vous qu'un produit scalaire est le grossissement d'un vecteur projeté sur un autre. Le produit scalaire d'un vecteur avec lui-même ne nécessite aucune projection, car il n'y a pas de différence de direction.[5] Cela signifie que • = ||une||2. Utilisez ce fait pour réécrire l'équation: - ( - ) • ( - ) = • + • - 2||une|| ||b||cos(θ)
-
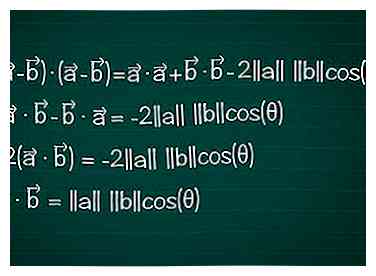 6 Réécrivez-le dans la formule familière. Développez le côté gauche de la formule, puis simplifiez-vous pour atteindre la formule utilisée pour trouver les angles.
6 Réécrivez-le dans la formule familière. Développez le côté gauche de la formule, puis simplifiez-vous pour atteindre la formule utilisée pour trouver les angles. - • - • - • + • = • + • - 2||une|| ||b||cos(θ)
- - • - • = -2||une|| ||b||cos(θ)
- -2( • ) = -2||une|| ||b||cos(θ)
- • = ||une|| ||b||cos(θ)
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
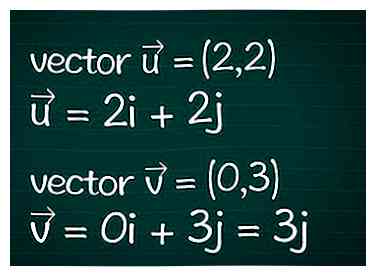 1 Identifier les vecteurs. Notez toutes les informations que vous avez concernant les deux vecteurs. Nous supposerons que vous avez uniquement la définition du vecteur en termes de coordonnées dimensionnelles (également appelées composants). Si vous connaissez déjà la longueur d'un vecteur (son ampleur), vous pourrez ignorer certaines des étapes ci-dessous.
1 Identifier les vecteurs. Notez toutes les informations que vous avez concernant les deux vecteurs. Nous supposerons que vous avez uniquement la définition du vecteur en termes de coordonnées dimensionnelles (également appelées composants). Si vous connaissez déjà la longueur d'un vecteur (son ampleur), vous pourrez ignorer certaines des étapes ci-dessous. 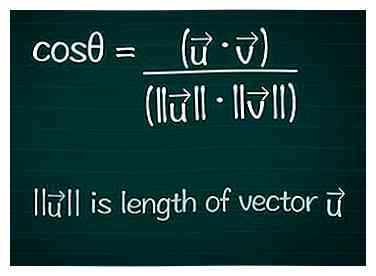 2 Notez la formule du cosinus. Pour trouver l'angle θ entre deux vecteurs, commencez par la formule pour trouver le cosinus de cet angle. Vous pouvez en apprendre davantage sur cette formule ci-dessous, ou simplement la noter:[1]
2 Notez la formule du cosinus. Pour trouver l'angle θ entre deux vecteurs, commencez par la formule pour trouver le cosinus de cet angle. Vous pouvez en apprendre davantage sur cette formule ci-dessous, ou simplement la noter:[1] 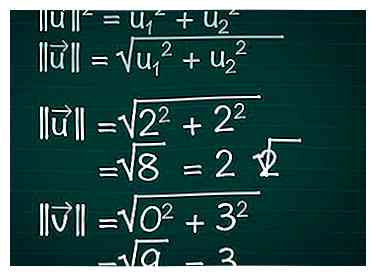 3 Calculez la longueur de chaque vecteur. Imaginez un triangle rectangle tiré du composant x du vecteur, de sa composante y et du vecteur lui-même. Le vecteur forme l'hypoténuse du triangle. Pour trouver sa longueur, nous utilisons le théorème de Pythagore. Il s'avère que cette formule est facilement étendue aux vecteurs avec un nombre quelconque de composants.
3 Calculez la longueur de chaque vecteur. Imaginez un triangle rectangle tiré du composant x du vecteur, de sa composante y et du vecteur lui-même. Le vecteur forme l'hypoténuse du triangle. Pour trouver sa longueur, nous utilisons le théorème de Pythagore. Il s'avère que cette formule est facilement étendue aux vecteurs avec un nombre quelconque de composants.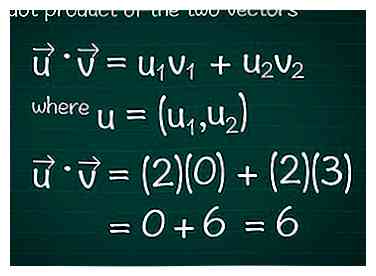 4 Calculez le produit scalaire des deux vecteurs. Vous avez probablement déjà appris cette méthode de multiplication de vecteurs, également appelée produit scalaire.[2]Pour calculer le produit scalaire en fonction des composants des vecteurs, multipliez les composants dans chaque direction, puis ajoutez tous les résultats. Pour les programmes graphiques, voir Astuces avant de continuer.
4 Calculez le produit scalaire des deux vecteurs. Vous avez probablement déjà appris cette méthode de multiplication de vecteurs, également appelée produit scalaire.[2]Pour calculer le produit scalaire en fonction des composants des vecteurs, multipliez les composants dans chaque direction, puis ajoutez tous les résultats. Pour les programmes graphiques, voir Astuces avant de continuer.  5 Branchez vos résultats dans la formule. Rappelez-vous, cosθ = (
5 Branchez vos résultats dans la formule. Rappelez-vous, cosθ = (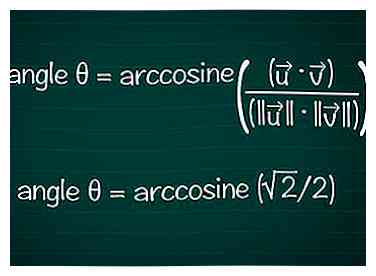 6 Trouvez l'angle basé sur le cosinus. Vous pouvez utiliser le
6 Trouvez l'angle basé sur le cosinus. Vous pouvez utiliser le  1 Comprendre le but de cette formule. Cette formule n'a pas été dérivée des règles existantes. Au lieu de cela, il a été créé comme une définition du produit scalaire de deux vecteurs et de l'angle entre eux.[3] Cependant, cette décision n'était pas arbitraire.En revenant à la géométrie de base, nous pouvons voir pourquoi cette formule donne des définitions intuitives et utiles.
1 Comprendre le but de cette formule. Cette formule n'a pas été dérivée des règles existantes. Au lieu de cela, il a été créé comme une définition du produit scalaire de deux vecteurs et de l'angle entre eux.[3] Cependant, cette décision n'était pas arbitraire.En revenant à la géométrie de base, nous pouvons voir pourquoi cette formule donne des définitions intuitives et utiles. 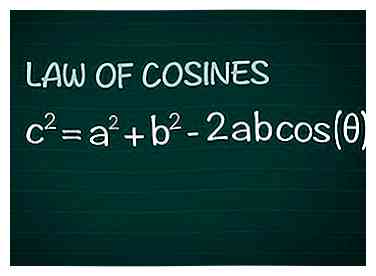 2 Passez en revue la loi des cosinus. Prenez un triangle ordinaire avec un angle θ entre les côtés a et b et le côté opposé c. La loi des cosinus stipule que c2 = a2 + b2 -2abcos(θ). Cela découle assez facilement de la géométrie de base.
2 Passez en revue la loi des cosinus. Prenez un triangle ordinaire avec un angle θ entre les côtés a et b et le côté opposé c. La loi des cosinus stipule que c2 = a2 + b2 -2abcos(θ). Cela découle assez facilement de la géométrie de base.  3 Connectez deux vecteurs pour former un triangle. Esquisser une paire de vecteurs 2D sur papier, vecteurs
3 Connectez deux vecteurs pour former un triangle. Esquisser une paire de vecteurs 2D sur papier, vecteurs 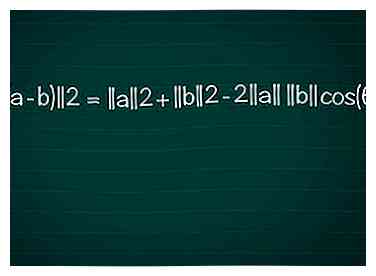 4 Écrivez la loi des cosinus pour ce triangle. Insérez la longueur de nos côtés "triangle vectoriel" dans la loi des cosinus:
4 Écrivez la loi des cosinus pour ce triangle. Insérez la longueur de nos côtés "triangle vectoriel" dans la loi des cosinus: 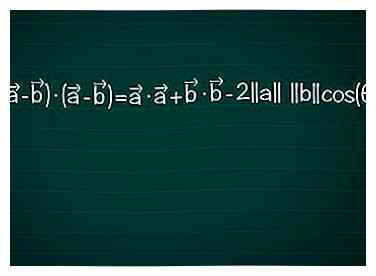 5 Ecrivez ceci en utilisant des produits scalaires. Rappelez-vous qu'un produit scalaire est le grossissement d'un vecteur projeté sur un autre. Le produit scalaire d'un vecteur avec lui-même ne nécessite aucune projection, car il n'y a pas de différence de direction.[5] Cela signifie que
5 Ecrivez ceci en utilisant des produits scalaires. Rappelez-vous qu'un produit scalaire est le grossissement d'un vecteur projeté sur un autre. Le produit scalaire d'un vecteur avec lui-même ne nécessite aucune projection, car il n'y a pas de différence de direction.[5] Cela signifie que 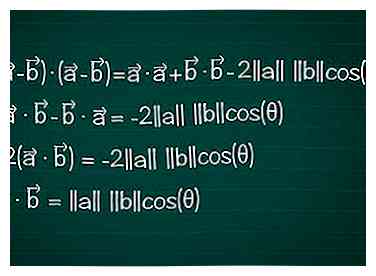 6 Réécrivez-le dans la formule familière. Développez le côté gauche de la formule, puis simplifiez-vous pour atteindre la formule utilisée pour trouver les angles.
6 Réécrivez-le dans la formule familière. Développez le côté gauche de la formule, puis simplifiez-vous pour atteindre la formule utilisée pour trouver les angles.