Les asymptotes d'une hyperbole sont les lignes qui traversent le centre de l'hyperbole. L'hyperbole se rapproche de plus en plus des asymptotes, mais ne peut jamais les atteindre. Il existe deux approches différentes que vous pouvez utiliser pour trouver les asymptotes. Apprendre à faire les deux peut vous aider à comprendre le concept.
Méthode One of Two:
L'affacturage
-
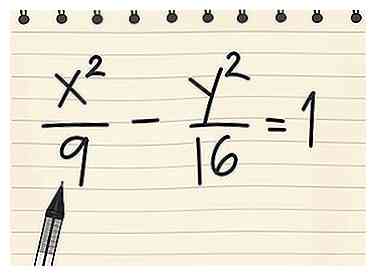 1 Notez l'équation de l'hyperbole dans sa forme standard. Commençons par un exemple simple: une hyperbole au centre de son origine. Pour ces hyperboles, la forme standard de l’équation est X2/une2 - y2/b2 = 1 pour les hyperboles qui s'étendent à droite et à gauche, ou y2/b2 - X2/une2 = 1 pour les hyperboles qui montent et descendent.[1] Rappelez-vous que x et y sont des variables, tandis que a et b sont des constantes (nombres ordinaires).
1 Notez l'équation de l'hyperbole dans sa forme standard. Commençons par un exemple simple: une hyperbole au centre de son origine. Pour ces hyperboles, la forme standard de l’équation est X2/une2 - y2/b2 = 1 pour les hyperboles qui s'étendent à droite et à gauche, ou y2/b2 - X2/une2 = 1 pour les hyperboles qui montent et descendent.[1] Rappelez-vous que x et y sont des variables, tandis que a et b sont des constantes (nombres ordinaires). - Exemple 1: X2/9 - y2/16 = 1
- Certains manuels et enseignants changent la position de a et b dans ces équations.[2] Suivez l'équation de près afin de comprendre ce qui se passe. Si vous ne faites que mémoriser les équations, vous ne serez pas préparé lorsque vous verrez une notation différente.
-
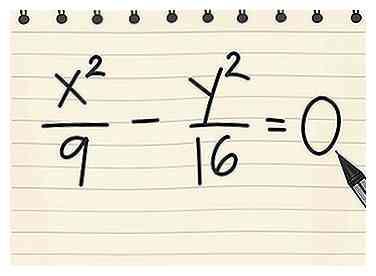 2 Définissez l'équation égale à zéro au lieu d'un. Cette nouvelle équation représente les deux asymptotes, mais il faudra un peu plus de travail pour les séparer.[3]
2 Définissez l'équation égale à zéro au lieu d'un. Cette nouvelle équation représente les deux asymptotes, mais il faudra un peu plus de travail pour les séparer.[3] - Exemple 1: X2/9 - y2/16 = 0
-
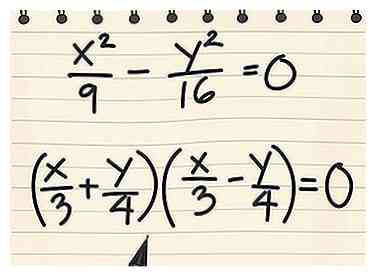 3 Facteur la nouvelle équation. Facturer le côté gauche de l'équation en deux produits. Rafraîchissez votre mémoire en factorisant un quadratique si vous en avez besoin, ou suivez-nous pendant que nous continuons Exemple 1:
3 Facteur la nouvelle équation. Facturer le côté gauche de l'équation en deux produits. Rafraîchissez votre mémoire en factorisant un quadratique si vous en avez besoin, ou suivez-nous pendant que nous continuons Exemple 1: - Nous allons nous retrouver avec une équation dans la forme (__ ± __)(__ ± __) = 0.
- Les deux premiers termes doivent se multiplier pour faire X2/9, alors prenez la racine carrée et écrivez-la dans ces espaces: (X/3 ± __)(X/3 ± __) = 0
- De même, prenez la racine carrée de y2/16 et placez-le dans les deux espaces restants: (X/3 ± y/4)(X/3 ± y/4) = 0
- Comme il n'y a pas d'autres termes, écrivez un signe plus et un signe moins pour que les autres termes s'annulent lorsqu'ils sont multipliés: (X/3 + y/4)(X/3 - y/4) = 0
-
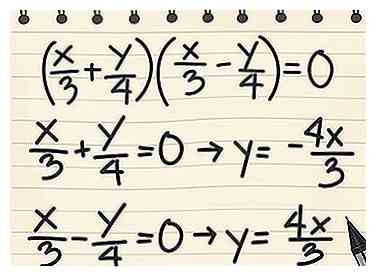 4 Séparez les facteurs et résolvez pour y. Pour obtenir les équations des asymptotes, séparez les deux facteurs et résolvez en termes de y.
4 Séparez les facteurs et résolvez pour y. Pour obtenir les équations des asymptotes, séparez les deux facteurs et résolvez en termes de y. - Exemple 1: Depuis (X/3 + y/4)(X/3 - y/4) = 0, nous savons X/3 + y/4 = 0 et X/3 - y/4 = 0
- Récrire X/3 + y/4 = 0 → y/4 = - X/3 → y = - 4x/3
- Récrire X/3 - y/4 = 0 → - y/4 = - X/3 → y = 4x/3
-
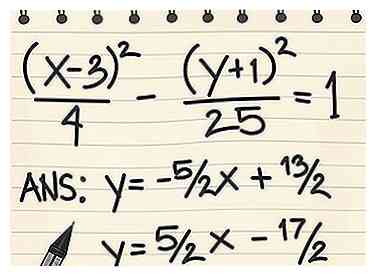 5 Essayez le même processus avec une équation plus difficile. Nous venons de trouver les asymptotes pour une hyperbole centrée sur l'origine. Une hyperbole centrée à (h, k) a une équation dans la forme (x - h)2/une2 - (y - k)2/b2 = 1, ou sous la forme (y - k)2/b2 - (x - h)2/une2 = 1. Vous pouvez les résoudre avec exactement la même méthode de factorisation décrite ci-dessus. Laissez simplement les termes (x - h) et (y - k) intacts jusqu'à la dernière étape.
5 Essayez le même processus avec une équation plus difficile. Nous venons de trouver les asymptotes pour une hyperbole centrée sur l'origine. Une hyperbole centrée à (h, k) a une équation dans la forme (x - h)2/une2 - (y - k)2/b2 = 1, ou sous la forme (y - k)2/b2 - (x - h)2/une2 = 1. Vous pouvez les résoudre avec exactement la même méthode de factorisation décrite ci-dessus. Laissez simplement les termes (x - h) et (y - k) intacts jusqu'à la dernière étape. - Exemple 2: (x - 3)2/4 - (y + 1)2/25 = 1
- Définissez cette valeur égale à 0 et facteur à obtenir:
- ((x - 3)/2 + (y + 1)/5)((x - 3)/2 - (y + 1)/5) = 0
- Séparer chaque facteur et résoudre pour trouver les équations des asymptotes:
- (x - 3)/2 + (y + 1)/5 = 0 → y = -5/2x + 13/2
- ((x - 3)/2 - (y + 1)/5) = 0 → y = 5/2X - 17/2
Méthode deux sur deux:
Résoudre pour Y
-
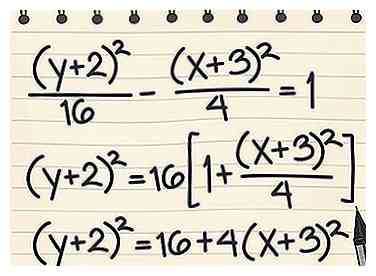 1 Notez l'équation de l'hyperbole avec y2 terme sur le côté gauche. Cette méthode est utile si vous avez une équation sous forme quadratique générale. Même si elle est de forme standard pour les hyperboles, cette approche peut vous donner un aperçu de la nature des asymptotes. Réorganiser l'équation de sorte que le y2 ou (y - k)2 terme est d'un côté pour commencer.
1 Notez l'équation de l'hyperbole avec y2 terme sur le côté gauche. Cette méthode est utile si vous avez une équation sous forme quadratique générale. Même si elle est de forme standard pour les hyperboles, cette approche peut vous donner un aperçu de la nature des asymptotes. Réorganiser l'équation de sorte que le y2 ou (y - k)2 terme est d'un côté pour commencer. - Exemple 3: (y + 2)2/16 - (x + 3)2/4 = 1
- Ajoutez le terme x aux deux côtés, puis multipliez chaque côté par 16:
- (y + 2)2 = 16(1 + (x + 3)2/4)
- Simplifier:
- (y + 2)2 = 16 + 4 (x + 3)2
-
 2 Prenez la racine carrée de chaque côté. Prenez la racine carrée, mais n'essayez pas encore de simplifier le côté droit. Rappelez-vous, lorsque vous prenez la racine carrée, il existe deux solutions possibles: une positive et une négative. (Par exemple, -2 * -2 = 4, donc √4 peut être égal à -2, ainsi que 2.) Utilisez le signe "+ ou -" ± pour suivre les deux solutions.
2 Prenez la racine carrée de chaque côté. Prenez la racine carrée, mais n'essayez pas encore de simplifier le côté droit. Rappelez-vous, lorsque vous prenez la racine carrée, il existe deux solutions possibles: une positive et une négative. (Par exemple, -2 * -2 = 4, donc √4 peut être égal à -2, ainsi que 2.) Utilisez le signe "+ ou -" ± pour suivre les deux solutions. - √ ((y + 2)2) = √ (16 + 4 (x + 3)2)
- (y + 2) = ± √ (16 + 4 (x + 3)2)
-
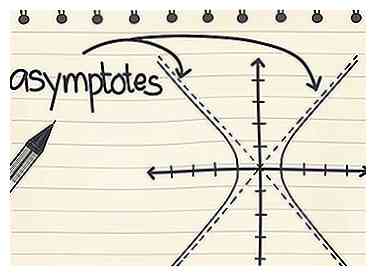 3 Passez en revue la définition d'une asymptote. Il est important que vous compreniez cela avant de continuer à l'étape suivante. L'asymptote d'une hyperbole est une ligne que l'hyperbole se rapproche de plus en plus lorsque x augmente. X ne peut jamais réellement atteindre l'asymptote, mais si nous suivons l'hyperbole pour des valeurs de plus en plus grandes de x, nous nous rapprocherons de plus en plus de l'asymptote.
3 Passez en revue la définition d'une asymptote. Il est important que vous compreniez cela avant de continuer à l'étape suivante. L'asymptote d'une hyperbole est une ligne que l'hyperbole se rapproche de plus en plus lorsque x augmente. X ne peut jamais réellement atteindre l'asymptote, mais si nous suivons l'hyperbole pour des valeurs de plus en plus grandes de x, nous nous rapprocherons de plus en plus de l'asymptote. -
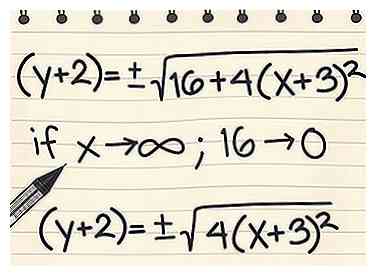 4 Ajustez l'équation pour les grandes valeurs de x. Puisque nous essayons de trouver l'équation asymptote maintenant, nous nous intéressons uniquement à x pour les très grandes valeurs ("approche de l'infini"). Cela nous permet d'ignorer certaines constantes de l'équation, car elles contribuent à une si petite partie par rapport au terme x. Une fois que x est à 99 milliards (par exemple), ajouter trois est tellement petit que nous pouvons l'ignorer.
4 Ajustez l'équation pour les grandes valeurs de x. Puisque nous essayons de trouver l'équation asymptote maintenant, nous nous intéressons uniquement à x pour les très grandes valeurs ("approche de l'infini"). Cela nous permet d'ignorer certaines constantes de l'équation, car elles contribuent à une si petite partie par rapport au terme x. Une fois que x est à 99 milliards (par exemple), ajouter trois est tellement petit que nous pouvons l'ignorer. - Dans l'équation (y + 2) = ± √ (16 + 4 (x + 3)2), à mesure que x se rapproche de l'infini, le 16 devient sans objet.
- (y + 2) = approximativement ± √ (4 (x + 3)2) pour les grandes valeurs de x
-
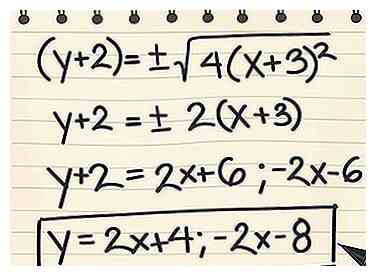 5 Résoudre pour y trouver les deux équations asymptotes. Maintenant que nous avons supprimé la constante, nous pouvons simplifier la racine carrée. Résoudre en termes de y pour obtenir la réponse. N'oubliez pas de diviser le symbole ± en deux équations distinctes, l'une avec + et l'autre avec -.
5 Résoudre pour y trouver les deux équations asymptotes. Maintenant que nous avons supprimé la constante, nous pouvons simplifier la racine carrée. Résoudre en termes de y pour obtenir la réponse. N'oubliez pas de diviser le symbole ± en deux équations distinctes, l'une avec + et l'autre avec -. - y + 2 = ± √ (4 (x + 3) ^ 2)
- y + 2 = ± 2 (x + 3)
- y + 2 = 2x + 6 et y + 2 = -2x - 6
- y = 2x + 4 et y = -2x - 8
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
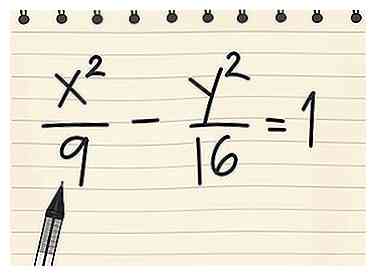 1 Notez l'équation de l'hyperbole dans sa forme standard. Commençons par un exemple simple: une hyperbole au centre de son origine. Pour ces hyperboles, la forme standard de l’équation est X2/une2 - y2/b2 = 1 pour les hyperboles qui s'étendent à droite et à gauche, ou y2/b2 - X2/une2 = 1 pour les hyperboles qui montent et descendent.[1] Rappelez-vous que x et y sont des variables, tandis que a et b sont des constantes (nombres ordinaires).
1 Notez l'équation de l'hyperbole dans sa forme standard. Commençons par un exemple simple: une hyperbole au centre de son origine. Pour ces hyperboles, la forme standard de l’équation est X2/une2 - y2/b2 = 1 pour les hyperboles qui s'étendent à droite et à gauche, ou y2/b2 - X2/une2 = 1 pour les hyperboles qui montent et descendent.[1] Rappelez-vous que x et y sont des variables, tandis que a et b sont des constantes (nombres ordinaires). 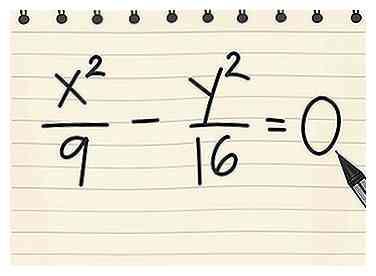 2 Définissez l'équation égale à zéro au lieu d'un. Cette nouvelle équation représente les deux asymptotes, mais il faudra un peu plus de travail pour les séparer.[3]
2 Définissez l'équation égale à zéro au lieu d'un. Cette nouvelle équation représente les deux asymptotes, mais il faudra un peu plus de travail pour les séparer.[3] 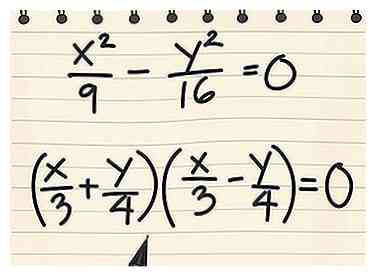 3 Facteur la nouvelle équation. Facturer le côté gauche de l'équation en deux produits. Rafraîchissez votre mémoire en factorisant un quadratique si vous en avez besoin, ou suivez-nous pendant que nous continuons Exemple 1:
3 Facteur la nouvelle équation. Facturer le côté gauche de l'équation en deux produits. Rafraîchissez votre mémoire en factorisant un quadratique si vous en avez besoin, ou suivez-nous pendant que nous continuons Exemple 1: 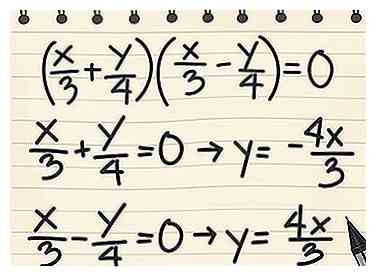 4 Séparez les facteurs et résolvez pour y. Pour obtenir les équations des asymptotes, séparez les deux facteurs et résolvez en termes de y.
4 Séparez les facteurs et résolvez pour y. Pour obtenir les équations des asymptotes, séparez les deux facteurs et résolvez en termes de y. 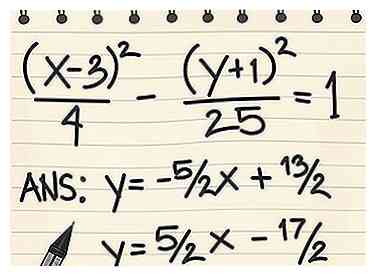 5 Essayez le même processus avec une équation plus difficile. Nous venons de trouver les asymptotes pour une hyperbole centrée sur l'origine. Une hyperbole centrée à (h, k) a une équation dans la forme (x - h)2/une2 - (y - k)2/b2 = 1, ou sous la forme (y - k)2/b2 - (x - h)2/une2 = 1. Vous pouvez les résoudre avec exactement la même méthode de factorisation décrite ci-dessus. Laissez simplement les termes (x - h) et (y - k) intacts jusqu'à la dernière étape.
5 Essayez le même processus avec une équation plus difficile. Nous venons de trouver les asymptotes pour une hyperbole centrée sur l'origine. Une hyperbole centrée à (h, k) a une équation dans la forme (x - h)2/une2 - (y - k)2/b2 = 1, ou sous la forme (y - k)2/b2 - (x - h)2/une2 = 1. Vous pouvez les résoudre avec exactement la même méthode de factorisation décrite ci-dessus. Laissez simplement les termes (x - h) et (y - k) intacts jusqu'à la dernière étape. 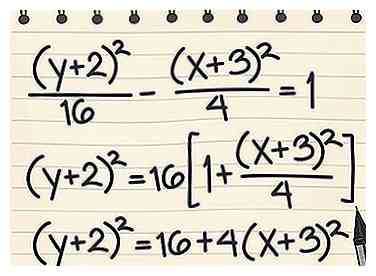 1 Notez l'équation de l'hyperbole avec y2 terme sur le côté gauche. Cette méthode est utile si vous avez une équation sous forme quadratique générale. Même si elle est de forme standard pour les hyperboles, cette approche peut vous donner un aperçu de la nature des asymptotes. Réorganiser l'équation de sorte que le y2 ou (y - k)2 terme est d'un côté pour commencer.
1 Notez l'équation de l'hyperbole avec y2 terme sur le côté gauche. Cette méthode est utile si vous avez une équation sous forme quadratique générale. Même si elle est de forme standard pour les hyperboles, cette approche peut vous donner un aperçu de la nature des asymptotes. Réorganiser l'équation de sorte que le y2 ou (y - k)2 terme est d'un côté pour commencer.  2 Prenez la racine carrée de chaque côté. Prenez la racine carrée, mais n'essayez pas encore de simplifier le côté droit. Rappelez-vous, lorsque vous prenez la racine carrée, il existe deux solutions possibles: une positive et une négative. (Par exemple, -2 * -2 = 4, donc √4 peut être égal à -2, ainsi que 2.) Utilisez le signe "+ ou -" ± pour suivre les deux solutions.
2 Prenez la racine carrée de chaque côté. Prenez la racine carrée, mais n'essayez pas encore de simplifier le côté droit. Rappelez-vous, lorsque vous prenez la racine carrée, il existe deux solutions possibles: une positive et une négative. (Par exemple, -2 * -2 = 4, donc √4 peut être égal à -2, ainsi que 2.) Utilisez le signe "+ ou -" ± pour suivre les deux solutions.  3 Passez en revue la définition d'une asymptote. Il est important que vous compreniez cela avant de continuer à l'étape suivante. L'asymptote d'une hyperbole est une ligne que l'hyperbole se rapproche de plus en plus lorsque x augmente. X ne peut jamais réellement atteindre l'asymptote, mais si nous suivons l'hyperbole pour des valeurs de plus en plus grandes de x, nous nous rapprocherons de plus en plus de l'asymptote.
3 Passez en revue la définition d'une asymptote. Il est important que vous compreniez cela avant de continuer à l'étape suivante. L'asymptote d'une hyperbole est une ligne que l'hyperbole se rapproche de plus en plus lorsque x augmente. X ne peut jamais réellement atteindre l'asymptote, mais si nous suivons l'hyperbole pour des valeurs de plus en plus grandes de x, nous nous rapprocherons de plus en plus de l'asymptote. 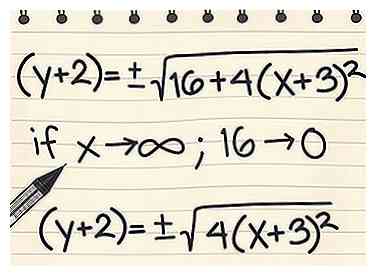 4 Ajustez l'équation pour les grandes valeurs de x. Puisque nous essayons de trouver l'équation asymptote maintenant, nous nous intéressons uniquement à x pour les très grandes valeurs ("approche de l'infini"). Cela nous permet d'ignorer certaines constantes de l'équation, car elles contribuent à une si petite partie par rapport au terme x. Une fois que x est à 99 milliards (par exemple), ajouter trois est tellement petit que nous pouvons l'ignorer.
4 Ajustez l'équation pour les grandes valeurs de x. Puisque nous essayons de trouver l'équation asymptote maintenant, nous nous intéressons uniquement à x pour les très grandes valeurs ("approche de l'infini"). Cela nous permet d'ignorer certaines constantes de l'équation, car elles contribuent à une si petite partie par rapport au terme x. Une fois que x est à 99 milliards (par exemple), ajouter trois est tellement petit que nous pouvons l'ignorer. 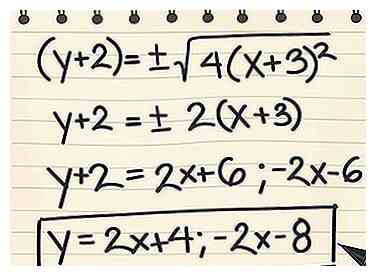 5 Résoudre pour y trouver les deux équations asymptotes. Maintenant que nous avons supprimé la constante, nous pouvons simplifier la racine carrée. Résoudre en termes de y pour obtenir la réponse. N'oubliez pas de diviser le symbole ± en deux équations distinctes, l'une avec + et l'autre avec -.
5 Résoudre pour y trouver les deux équations asymptotes. Maintenant que nous avons supprimé la constante, nous pouvons simplifier la racine carrée. Résoudre en termes de y pour obtenir la réponse. N'oubliez pas de diviser le symbole ± en deux équations distinctes, l'une avec + et l'autre avec -.