Un vecteur est un objet géométrique qui a à la fois une ampleur et une direction.[1] La magnitude est la longueur du vecteur, alors que la direction est la façon dont elle pointe. Calculer la magnitude d’un vecteur est simple en quelques étapes simples. D'autres opérations vectorielles importantes comprennent l'ajout et la soustraction de vecteurs, la recherche de l'angle entre deux vecteurs et la recherche du produit croisé.
Méthode One of Two:
Trouver la magnitude d'un vecteur à l'origine
-
 1 Détermine les composants du vecteur. Chaque vecteur peut être représenté numériquement dans le système de coordonnées cartésiennes par une composante horizontale (axe des abscisses) et verticale (axe des ordonnées).[2] Il est écrit comme une paire ordonnée .
1 Détermine les composants du vecteur. Chaque vecteur peut être représenté numériquement dans le système de coordonnées cartésiennes par une composante horizontale (axe des abscisses) et verticale (axe des ordonnées).[2] Il est écrit comme une paire ordonnée . - Par exemple, le vecteur ci-dessus a une composante horizontale de 3 et une composante verticale de -5, donc la paire ordonnée est <3, -5>.
-
 2 Dessine un triangle vectoriel. Lorsque vous dessinez les composants horizontaux et verticaux, vous vous retrouvez avec un triangle rectangle. La magnitude du vecteur est égale à l’hypoténuse du triangle, vous pouvez donc utiliser le théorème de Pythagore pour le calculer.
2 Dessine un triangle vectoriel. Lorsque vous dessinez les composants horizontaux et verticaux, vous vous retrouvez avec un triangle rectangle. La magnitude du vecteur est égale à l’hypoténuse du triangle, vous pouvez donc utiliser le théorème de Pythagore pour le calculer. -
 3 Réorganiser le théorème de Pythagore pour calculer la magnitude. Le théorème de Pythagore est A2 + B2 = C2. "A" et "B" sont les composantes horizontales et verticales du triangle tandis que "C" est l'hypoténuse. Puisque le vecteur est l'hypoténuse que vous voulez résoudre pour «C».
3 Réorganiser le théorème de Pythagore pour calculer la magnitude. Le théorème de Pythagore est A2 + B2 = C2. "A" et "B" sont les composantes horizontales et verticales du triangle tandis que "C" est l'hypoténuse. Puisque le vecteur est l'hypoténuse que vous voulez résoudre pour «C». - X2 + y2 = v2
- v = √ (x2 + y2))
-
 4 Résoudre l'ampleur. En utilisant l'équation ci-dessus, vous pouvez brancher les nombres de la paire ordonnée du vecteur à résoudre pour la magnitude.
4 Résoudre l'ampleur. En utilisant l'équation ci-dessus, vous pouvez brancher les nombres de la paire ordonnée du vecteur à résoudre pour la magnitude. - Par exemple, v = √ ((32+(-5)2))
- v = √ (9 + 25) = √34 = 5.831
- Ne vous inquiétez pas si votre réponse n'est pas un nombre entier. Les grandeurs vectorielles peuvent être des décimales.
Méthode deux sur deux:
Trouver la magnitude d'un vecteur éloigné de l'origine
-
 1 Détermine les composants des deux points du vecteur. Chaque vecteur peut être représenté numériquement dans le système de coordonnées cartésiennes par une composante horizontale (axe des abscisses) et verticale (axe des ordonnées).[3] Il est écrit comme une paire ordonnée . Si un vecteur est placé loin de l'origine du système de coordonnées cartésiennes, vous devez définir les composants des deux points du vecteur.
1 Détermine les composants des deux points du vecteur. Chaque vecteur peut être représenté numériquement dans le système de coordonnées cartésiennes par une composante horizontale (axe des abscisses) et verticale (axe des ordonnées).[3] Il est écrit comme une paire ordonnée . Si un vecteur est placé loin de l'origine du système de coordonnées cartésiennes, vous devez définir les composants des deux points du vecteur. - Par exemple, le vecteur AB a une paire ordonnée pour les points A et B.
- Le point A a une composante horizontale de 5 et une composante verticale de 1, donc la paire ordonnée est <5, 1>.
- Le point B a une composante horizontale de 1 et une composante verticale de 2, donc la paire ordonnée est <1, 2>.
-
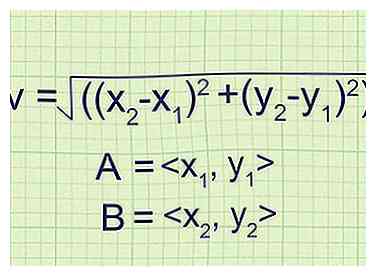 2 Utilisez une formule modifiée pour résoudre l'ampleur. Étant donné que vous avez maintenant deux points, vous devez soustraire les composantes x et y de chaque point avant de résoudre en utilisant l'équation v = √ ((x2-X1)2 + (y2-y1)2).[4]
2 Utilisez une formule modifiée pour résoudre l'ampleur. Étant donné que vous avez maintenant deux points, vous devez soustraire les composantes x et y de chaque point avant de résoudre en utilisant l'équation v = √ ((x2-X1)2 + (y2-y1)2).[4] - Le point A est une paire ordonnée 1 <>1, y1> et le point B est commandé par paire 2 <>2, y2>
-
 3 Résoudre l'ampleur. Branchez les numéros de vos paires ordonnées et calculez la magnitude. En utilisant notre exemple ci-dessus, le calcul ressemble à ceci:
3 Résoudre l'ampleur. Branchez les numéros de vos paires ordonnées et calculez la magnitude. En utilisant notre exemple ci-dessus, le calcul ressemble à ceci: - v = √ ((x2-X1)2 + (y2-y1)2)
- v = √ ((1-5)2 +(2-1)2)
- v = √ ((- 4)2 +(1)2)
- v = √ (16 + 1) = √ (17) = 4,12
- Ne vous inquiétez pas si votre réponse n'est pas un nombre entier. Les grandeurs vectorielles peuvent être des décimales.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Détermine les composants du vecteur. Chaque vecteur peut être représenté numériquement dans le système de coordonnées cartésiennes par une composante horizontale (axe des abscisses) et verticale (axe des ordonnées).[2] Il est écrit comme une paire ordonnée
1 Détermine les composants du vecteur. Chaque vecteur peut être représenté numériquement dans le système de coordonnées cartésiennes par une composante horizontale (axe des abscisses) et verticale (axe des ordonnées).[2] Il est écrit comme une paire ordonnée  2 Dessine un triangle vectoriel. Lorsque vous dessinez les composants horizontaux et verticaux, vous vous retrouvez avec un triangle rectangle. La magnitude du vecteur est égale à l’hypoténuse du triangle, vous pouvez donc utiliser le théorème de Pythagore pour le calculer.
2 Dessine un triangle vectoriel. Lorsque vous dessinez les composants horizontaux et verticaux, vous vous retrouvez avec un triangle rectangle. La magnitude du vecteur est égale à l’hypoténuse du triangle, vous pouvez donc utiliser le théorème de Pythagore pour le calculer.  3 Réorganiser le théorème de Pythagore pour calculer la magnitude. Le théorème de Pythagore est A2 + B2 = C2. "A" et "B" sont les composantes horizontales et verticales du triangle tandis que "C" est l'hypoténuse. Puisque le vecteur est l'hypoténuse que vous voulez résoudre pour «C».
3 Réorganiser le théorème de Pythagore pour calculer la magnitude. Le théorème de Pythagore est A2 + B2 = C2. "A" et "B" sont les composantes horizontales et verticales du triangle tandis que "C" est l'hypoténuse. Puisque le vecteur est l'hypoténuse que vous voulez résoudre pour «C».  4 Résoudre l'ampleur. En utilisant l'équation ci-dessus, vous pouvez brancher les nombres de la paire ordonnée du vecteur à résoudre pour la magnitude.
4 Résoudre l'ampleur. En utilisant l'équation ci-dessus, vous pouvez brancher les nombres de la paire ordonnée du vecteur à résoudre pour la magnitude.  1 Détermine les composants des deux points du vecteur. Chaque vecteur peut être représenté numériquement dans le système de coordonnées cartésiennes par une composante horizontale (axe des abscisses) et verticale (axe des ordonnées).[3] Il est écrit comme une paire ordonnée
1 Détermine les composants des deux points du vecteur. Chaque vecteur peut être représenté numériquement dans le système de coordonnées cartésiennes par une composante horizontale (axe des abscisses) et verticale (axe des ordonnées).[3] Il est écrit comme une paire ordonnée 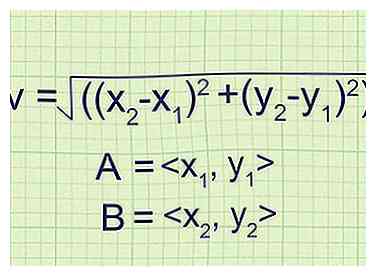 2 Utilisez une formule modifiée pour résoudre l'ampleur. Étant donné que vous avez maintenant deux points, vous devez soustraire les composantes x et y de chaque point avant de résoudre en utilisant l'équation v = √ ((x2-X1)2 + (y2-y1)2).[4]
2 Utilisez une formule modifiée pour résoudre l'ampleur. Étant donné que vous avez maintenant deux points, vous devez soustraire les composantes x et y de chaque point avant de résoudre en utilisant l'équation v = √ ((x2-X1)2 + (y2-y1)2).[4]  3 Résoudre l'ampleur. Branchez les numéros de vos paires ordonnées et calculez la magnitude. En utilisant notre exemple ci-dessus, le calcul ressemble à ceci:
3 Résoudre l'ampleur. Branchez les numéros de vos paires ordonnées et calculez la magnitude. En utilisant notre exemple ci-dessus, le calcul ressemble à ceci: