Le sommet d'une équation quadratique ou d'une parabole est le point le plus haut ou le plus bas de cette équation. Il repose également sur le plan de symétrie de la parabole entière; tout ce qui se trouve à gauche de la parabole est une image complète de ce qui est à droite. Si vous souhaitez trouver le sommet d'une équation quadratique, vous pouvez soit utiliser la formule de sommet, soit compléter le carré.
Méthode One of Two:
Utiliser la formule de vertex
-
 1 Identifiez les valeurs de a, b et c. Dans une équation quadratique, le X2 terme = une, la X terme = b, et le terme constant (le terme sans variable) = c. Disons que vous travaillez avec l'équation suivante: y = X2 + 9x + 18. Dans cet exemple, une = 1, b = 9 et c = 18.[1]
1 Identifiez les valeurs de a, b et c. Dans une équation quadratique, le X2 terme = une, la X terme = b, et le terme constant (le terme sans variable) = c. Disons que vous travaillez avec l'équation suivante: y = X2 + 9x + 18. Dans cet exemple, une = 1, b = 9 et c = 18.[1] -
 2 Utilisez la formule de sommet pour trouver la valeur x du sommet. Le sommet est aussi l'axe de symétrie de l'équation. La formule pour trouver la valeur x du sommet d'une équation quadratique est x = -b / 2a. Branchez les valeurs pertinentes à rechercher X. Remplacez les valeurs pour a et b. Montre ton travail:
2 Utilisez la formule de sommet pour trouver la valeur x du sommet. Le sommet est aussi l'axe de symétrie de l'équation. La formule pour trouver la valeur x du sommet d'une équation quadratique est x = -b / 2a. Branchez les valeurs pertinentes à rechercher X. Remplacez les valeurs pour a et b. Montre ton travail: - x = -b / 2a
- x = - (9) / (2) (1)
- x = -9 / 2
-
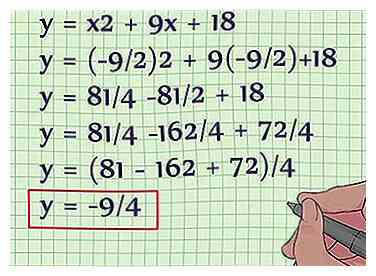 3 Branchez la valeur x dans l'équation d'origine pour obtenir la valeur y. Maintenant que vous connaissez la valeur x, branchez-la à la formule d'origine pour la valeur y. Vous pouvez penser à la formule pour trouver le sommet d'une fonction quadratique comme étant (x, y) = [(-b / 2a), f (-b / 2a)]. Cela signifie simplement que pour obtenir la valeur y, vous devez trouver la valeur x basée sur la formule, puis la réinsérer dans l'équation. Voici comment vous le faites:
3 Branchez la valeur x dans l'équation d'origine pour obtenir la valeur y. Maintenant que vous connaissez la valeur x, branchez-la à la formule d'origine pour la valeur y. Vous pouvez penser à la formule pour trouver le sommet d'une fonction quadratique comme étant (x, y) = [(-b / 2a), f (-b / 2a)]. Cela signifie simplement que pour obtenir la valeur y, vous devez trouver la valeur x basée sur la formule, puis la réinsérer dans l'équation. Voici comment vous le faites: - y = x2 + 9x + 18
- y = (-9/2)2 + 9(-9/2) +18
- y = 81/4 -81/2 + 18
- y = 81/4 -162/4 + 72/4
- y = (81 - 162 + 72) / 4
- y = -9/4
-
 4 Notez les valeurs x et y en tant que paire ordonnée. Maintenant que vous savez que x = -9/2 et y = -9/4, écrivez-les simplement en tant que paire ordonnée: (-9/2, -9/4). Le sommet de cette équation quadratique est (-9/2, -9/4). Si vous deviez dessiner cette parabole sur un graphique, ce point serait le minimum de la parabole, car le x2 le terme est positif.
4 Notez les valeurs x et y en tant que paire ordonnée. Maintenant que vous savez que x = -9/2 et y = -9/4, écrivez-les simplement en tant que paire ordonnée: (-9/2, -9/4). Le sommet de cette équation quadratique est (-9/2, -9/4). Si vous deviez dessiner cette parabole sur un graphique, ce point serait le minimum de la parabole, car le x2 le terme est positif.
Méthode deux sur deux:
Compléter la place
-
 1 Notez l'équation. Compléter le carré est une autre façon de trouver le sommet d'une équation quadratique. Pour cette méthode, lorsque vous arriverez à la fin, vous pourrez trouver vos coordonnées x et y immédiatement, au lieu de replacer la coordonnée x dans l'équation d'origine. Disons que vous travaillez avec l'équation quadratique suivante: X2 + 4x + 1 = 0.[2]
1 Notez l'équation. Compléter le carré est une autre façon de trouver le sommet d'une équation quadratique. Pour cette méthode, lorsque vous arriverez à la fin, vous pourrez trouver vos coordonnées x et y immédiatement, au lieu de replacer la coordonnée x dans l'équation d'origine. Disons que vous travaillez avec l'équation quadratique suivante: X2 + 4x + 1 = 0.[2] -
 2 Diviser chaque terme par le coefficient du terme x 2. Dans ce cas, le coefficient du terme x 2 est 1, vous pouvez donc sauter cette étape. Diviser chaque terme par 1 ne changerait rien. Diviser chaque terme par 0 changera cependant tout.
2 Diviser chaque terme par le coefficient du terme x 2. Dans ce cas, le coefficient du terme x 2 est 1, vous pouvez donc sauter cette étape. Diviser chaque terme par 1 ne changerait rien. Diviser chaque terme par 0 changera cependant tout. -
 3 Déplacez le terme constant vers le côté droit de l'équation. Le terme constant est le terme sans coefficient. Dans ce cas, c'est "1." Déplacer 1 de l'autre côté de l'équation en soustrayant 1 des deux côtés. Voici comment vous le faites:[3]
3 Déplacez le terme constant vers le côté droit de l'équation. Le terme constant est le terme sans coefficient. Dans ce cas, c'est "1." Déplacer 1 de l'autre côté de l'équation en soustrayant 1 des deux côtés. Voici comment vous le faites:[3] - X2 + 4x + 1 = 0
- X2 + 4x + 1 -1 = 0 - 1
- X2 + 4x = - 1
-
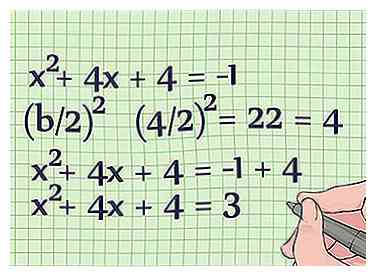 4 Remplissez le carré sur le côté gauche de l'équation. Pour ce faire, trouvez simplement (b / 2)2 et ajouter le résultat des deux côtés de l'équation. Branchez "4" pour b, puisque "4x" est le terme b de cette équation.
4 Remplissez le carré sur le côté gauche de l'équation. Pour ce faire, trouvez simplement (b / 2)2 et ajouter le résultat des deux côtés de l'équation. Branchez "4" pour b, puisque "4x" est le terme b de cette équation. - (4/2)2 = 22 = 4. Maintenant, ajoutez 4 aux deux côtés de l'équation pour obtenir ce qui suit:
- X2 + 4x + 4 = -1 + 4
- X2 + 4x + 4 = 3
- (4/2)2 = 22 = 4. Maintenant, ajoutez 4 aux deux côtés de l'équation pour obtenir ce qui suit:
-
 5 Facteur le côté gauche de l'équation. Maintenant, vous verrez que x2 + 4x + 4 est un carré parfait. Il peut être réécrit comme (x + 2)2 = 3
5 Facteur le côté gauche de l'équation. Maintenant, vous verrez que x2 + 4x + 4 est un carré parfait. Il peut être réécrit comme (x + 2)2 = 3 - 6 Utilisez ce format pour trouver les coordonnées x et y. Vous pouvez trouver votre coordonnée x en définissant simplement (x + 2) 2 égal à zéro. Alors, quand (x + 2) 2 = 0, qu'est-ce que x devrait être? La variable x devrait être -2 pour équilibrer le +2, donc votre coordonnée x est -2. Votre coordonnée y est simplement le terme constant de l'autre côté de l'équation. Donc, y = 3. Vous pouvez également faire un raccourci et simplement prendre le signe opposé du nombre entre parenthèses pour obtenir la coordonnée x. Donc, le sommet de l'équation x2 + 4x + 1 = (-2, -3)
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Identifiez les valeurs de a, b et c. Dans une équation quadratique, le X2 terme = une, la X terme = b, et le terme constant (le terme sans variable) = c. Disons que vous travaillez avec l'équation suivante: y = X2 + 9x + 18. Dans cet exemple, une = 1, b = 9 et c = 18.[1]
1 Identifiez les valeurs de a, b et c. Dans une équation quadratique, le X2 terme = une, la X terme = b, et le terme constant (le terme sans variable) = c. Disons que vous travaillez avec l'équation suivante: y = X2 + 9x + 18. Dans cet exemple, une = 1, b = 9 et c = 18.[1]  2 Utilisez la formule de sommet pour trouver la valeur x du sommet. Le sommet est aussi l'axe de symétrie de l'équation. La formule pour trouver la valeur x du sommet d'une équation quadratique est x = -b / 2a. Branchez les valeurs pertinentes à rechercher X. Remplacez les valeurs pour a et b. Montre ton travail:
2 Utilisez la formule de sommet pour trouver la valeur x du sommet. Le sommet est aussi l'axe de symétrie de l'équation. La formule pour trouver la valeur x du sommet d'une équation quadratique est x = -b / 2a. Branchez les valeurs pertinentes à rechercher X. Remplacez les valeurs pour a et b. Montre ton travail: 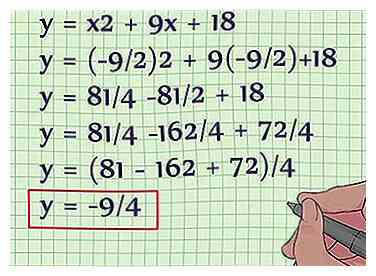 3 Branchez la valeur x dans l'équation d'origine pour obtenir la valeur y. Maintenant que vous connaissez la valeur x, branchez-la à la formule d'origine pour la valeur y. Vous pouvez penser à la formule pour trouver le sommet d'une fonction quadratique comme étant (x, y) = [(-b / 2a), f (-b / 2a)]. Cela signifie simplement que pour obtenir la valeur y, vous devez trouver la valeur x basée sur la formule, puis la réinsérer dans l'équation. Voici comment vous le faites:
3 Branchez la valeur x dans l'équation d'origine pour obtenir la valeur y. Maintenant que vous connaissez la valeur x, branchez-la à la formule d'origine pour la valeur y. Vous pouvez penser à la formule pour trouver le sommet d'une fonction quadratique comme étant (x, y) = [(-b / 2a), f (-b / 2a)]. Cela signifie simplement que pour obtenir la valeur y, vous devez trouver la valeur x basée sur la formule, puis la réinsérer dans l'équation. Voici comment vous le faites:  4 Notez les valeurs x et y en tant que paire ordonnée. Maintenant que vous savez que x = -9/2 et y = -9/4, écrivez-les simplement en tant que paire ordonnée: (-9/2, -9/4). Le sommet de cette équation quadratique est (-9/2, -9/4). Si vous deviez dessiner cette parabole sur un graphique, ce point serait le minimum de la parabole, car le x2 le terme est positif.
4 Notez les valeurs x et y en tant que paire ordonnée. Maintenant que vous savez que x = -9/2 et y = -9/4, écrivez-les simplement en tant que paire ordonnée: (-9/2, -9/4). Le sommet de cette équation quadratique est (-9/2, -9/4). Si vous deviez dessiner cette parabole sur un graphique, ce point serait le minimum de la parabole, car le x2 le terme est positif.  1 Notez l'équation. Compléter le carré est une autre façon de trouver le sommet d'une équation quadratique. Pour cette méthode, lorsque vous arriverez à la fin, vous pourrez trouver vos coordonnées x et y immédiatement, au lieu de replacer la coordonnée x dans l'équation d'origine. Disons que vous travaillez avec l'équation quadratique suivante: X2 + 4x + 1 = 0.[2]
1 Notez l'équation. Compléter le carré est une autre façon de trouver le sommet d'une équation quadratique. Pour cette méthode, lorsque vous arriverez à la fin, vous pourrez trouver vos coordonnées x et y immédiatement, au lieu de replacer la coordonnée x dans l'équation d'origine. Disons que vous travaillez avec l'équation quadratique suivante: X2 + 4x + 1 = 0.[2]  2 Diviser chaque terme par le coefficient du terme x 2. Dans ce cas, le coefficient du terme x 2 est 1, vous pouvez donc sauter cette étape. Diviser chaque terme par 1 ne changerait rien. Diviser chaque terme par 0 changera cependant tout.
2 Diviser chaque terme par le coefficient du terme x 2. Dans ce cas, le coefficient du terme x 2 est 1, vous pouvez donc sauter cette étape. Diviser chaque terme par 1 ne changerait rien. Diviser chaque terme par 0 changera cependant tout.  3 Déplacez le terme constant vers le côté droit de l'équation. Le terme constant est le terme sans coefficient. Dans ce cas, c'est "1." Déplacer 1 de l'autre côté de l'équation en soustrayant 1 des deux côtés. Voici comment vous le faites:[3]
3 Déplacez le terme constant vers le côté droit de l'équation. Le terme constant est le terme sans coefficient. Dans ce cas, c'est "1." Déplacer 1 de l'autre côté de l'équation en soustrayant 1 des deux côtés. Voici comment vous le faites:[3] 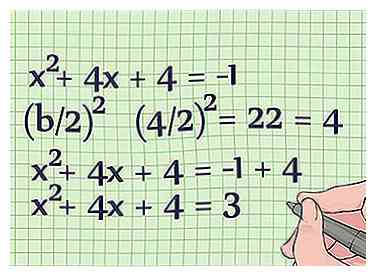 4 Remplissez le carré sur le côté gauche de l'équation. Pour ce faire, trouvez simplement (b / 2)2 et ajouter le résultat des deux côtés de l'équation. Branchez "4" pour b, puisque "4x" est le terme b de cette équation.
4 Remplissez le carré sur le côté gauche de l'équation. Pour ce faire, trouvez simplement (b / 2)2 et ajouter le résultat des deux côtés de l'équation. Branchez "4" pour b, puisque "4x" est le terme b de cette équation.  5 Facteur le côté gauche de l'équation. Maintenant, vous verrez que x2 + 4x + 4 est un carré parfait. Il peut être réécrit comme (x + 2)2 = 3
5 Facteur le côté gauche de l'équation. Maintenant, vous verrez que x2 + 4x + 4 est un carré parfait. Il peut être réécrit comme (x + 2)2 = 3