Une parabole est une courbe bidimensionnelle à symétrie miroir qui a la forme d'une arche. Tout point de la parabole est équidistant d'un point fixe (le foyer) et d'une ligne droite fixe (la directrice). Pour représenter graphiquement une parabole, vous devez trouver son sommet ainsi que plusieurs points de chaque côté du sommet afin de marquer le chemin parcouru par les points.
Première partie de deux:
Représentation graphique d'une parabole
-
 1 Comprendre les parties d'une parabole. Vous pouvez recevoir certaines informations avant de commencer et connaître la terminologie vous aidera à éviter les étapes inutiles. Voici les parties de la parabole à connaître: [1]
1 Comprendre les parties d'une parabole. Vous pouvez recevoir certaines informations avant de commencer et connaître la terminologie vous aidera à éviter les étapes inutiles. Voici les parties de la parabole à connaître: [1] - La mise au point. Un point fixe à l'intérieur de la parabole utilisé pour la définition formelle de la courbe.
- La directrice Une ligne droite fixe. La parabole est le lieu (série) de points dans lequel un point donné est à égale distance du concentrer et le directrice. (Voir le diagramme ci-dessus.)
- L'axe de symétrie. Il s'agit d'une ligne droite qui traverse le point tournant ("vertex") de la parabole et qui est à égale distance des points correspondants des deux bras de la parabole.
- Le sommet Le point où l'axe de symétrie traverse la parabole s'appelle le sommet de la parabole. Si la parabole s'ouvre vers le haut ou vers la droite, le sommet est un point minimum de la courbe. S'il s'ouvre vers le bas ou vers la gauche, le sommet est un point maximum
-
 2 Connaître l'équation d'une parabole. L'équation générale d'une parabole est y = hache2+ bx + c. Il peut également être écrit sous la forme encore plus générale y = a (x - h) ² + k, mais nous allons nous concentrer ici sur la première forme de l’équation.
2 Connaître l'équation d'une parabole. L'équation générale d'une parabole est y = hache2+ bx + c. Il peut également être écrit sous la forme encore plus générale y = a (x - h) ² + k, mais nous allons nous concentrer ici sur la première forme de l’équation. - Si le coefficient une dans l'équation est positive, la parabole s'ouvre vers le haut (dans une parabole orientée verticalement), comme la lettre "U", et son sommet est un point minimum. Si la une est négative, la parabole s'ouvre vers le bas et a un sommet à son point maximum. Si vous avez du mal à vous en souvenir, pensez-y de cette façon: une équation avec positif une la valeur ressemble à un sourire; une équation avec un négatif une la valeur ressemble à un froncement de sourcils. [2]
- Disons que vous avez l'équation suivante: y = 2x2 -1. Cette parabole aura la forme d'un "U" car la une La valeur (2) est positive.
- Si l'équation a un terme carré au lieu d'un carré x, la parabole sera orientée horizontalement et ouverte sur le côté, à droite ou à gauche, comme un "C" ou un "C" en arrière. Par exemple, la parabole y2 = x + 3 s'ouvre à droite, comme un "C"
-
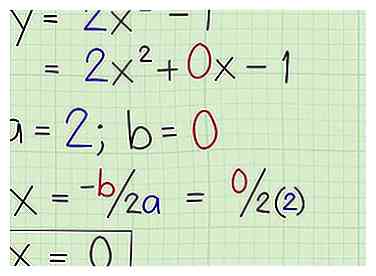 3 Trouvez l'axe de symétrie. Rappelez-vous que l'axe de symétrie est la ligne droite qui traverse le point tournant (sommet) de la parabole. Dans le cas d'une parabole verticale (ouverture ou descente), l'axe est identique à la coordonnée x du sommet, qui est la valeur x du point où l'axe de symétrie traverse la parabole. Pour trouver l'axe de symétrie, utilisez cette formule: x = -b / 2a. [3]
3 Trouvez l'axe de symétrie. Rappelez-vous que l'axe de symétrie est la ligne droite qui traverse le point tournant (sommet) de la parabole. Dans le cas d'une parabole verticale (ouverture ou descente), l'axe est identique à la coordonnée x du sommet, qui est la valeur x du point où l'axe de symétrie traverse la parabole. Pour trouver l'axe de symétrie, utilisez cette formule: x = -b / 2a. [3] - Dans l'exemple ci-dessus (y = 2x² -1), a = 2 et b = 0. Maintenant, vous pouvez calculer l'axe de symétrie en branchant les nombres: x = -0 / (2) (2) = 0.
- Dans ce cas, l'axe de symétrie est x = 0 (qui est l'axe des y du plan de coordonnées).
-
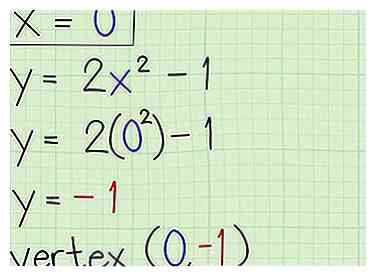 4 Trouvez le sommet. Une fois que vous connaissez l'axe de symétrie, vous pouvez brancher cette valeur pour que x obtienne la coordonnée y. Ces deux coordonnées vous donneront le sommet de la parabole. Dans ce cas, vous devez brancher 0 à 2x2 -1 pour obtenir la coordonnée y. y = 2 x 02 -1 = 0 -1 = -1. Le sommet est (0, -1) et la parabole traverse l'axe des y à -1. [4]
4 Trouvez le sommet. Une fois que vous connaissez l'axe de symétrie, vous pouvez brancher cette valeur pour que x obtienne la coordonnée y. Ces deux coordonnées vous donneront le sommet de la parabole. Dans ce cas, vous devez brancher 0 à 2x2 -1 pour obtenir la coordonnée y. y = 2 x 02 -1 = 0 -1 = -1. Le sommet est (0, -1) et la parabole traverse l'axe des y à -1. [4] - Les coordonnées du sommet sont parfois appelées (h, k). Dans ce cas h est 0, et k est -1. L'équation de la parabole peut être écrite sous la forme y = a (x - h) ² + k. Sous cette forme, le sommet est le point (h, k), et vous n'avez pas besoin de faire de calcul pour trouver le sommet au-delà de l'interprétation correcte du graphique.
-
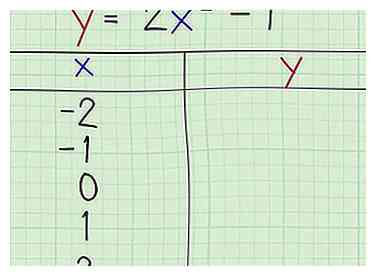 5 Configurez un tableau avec les valeurs choisies de x. Créez une table avec des valeurs particulières de x dans la première colonne. Ce tableau vous donnera les coordonnées dont vous avez besoin pour représenter l'équation.
5 Configurez un tableau avec les valeurs choisies de x. Créez une table avec des valeurs particulières de x dans la première colonne. Ce tableau vous donnera les coordonnées dont vous avez besoin pour représenter l'équation. - La valeur médiane de x doit être l'axe de symétrie dans le cas d'une parabole "verticale".
- Vous devez inclure au moins deux valeurs au-dessus et au-dessous de la valeur médiane pour x dans la table pour des raisons de symétrie.
- Dans cet exemple, placez la valeur de l'axe de symétrie (x = 0) au centre de la table.
-
 6 Calculez les valeurs des coordonnées y correspondantes. Remplacez chaque valeur de x dans l'équation de la parabole et calculez les valeurs correspondantes de y. Insérez ces valeurs calculées de y dans la table. Dans cet exemple, les valeurs de y sont calculées comme suit:
6 Calculez les valeurs des coordonnées y correspondantes. Remplacez chaque valeur de x dans l'équation de la parabole et calculez les valeurs correspondantes de y. Insérez ces valeurs calculées de y dans la table. Dans cet exemple, les valeurs de y sont calculées comme suit: - Pour x = -2, y est calculé comme suit: y = (2) (-2)2 - 1 = 8 - 1 = 7
- Pour x = -1, y est calculé comme suit: y = (2) (-1)2 - 1 = 2 - 1 = 1
- Pour x = 0, y est calculé comme suit: y = (2) (0)2 - 1 = 0 - 1 = -1
- Pour x = 1, y est calculé comme suit: y = (2) (1)2 - 1 = 2 - 1 = 1
- Pour x = 2, y est calculé comme suit: y = (2) (2)2 - 1 = 8 - 1 = 7
-
 7 Insérez les valeurs calculées de y dans la table. Maintenant que vous avez trouvé au moins cinq paires de coordonnées pour la parabole, vous êtes presque prêt à le représenter graphiquement. Sur la base de votre travail, vous avez maintenant les points suivants: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Rappelez-vous que la parabole est réfléchie (symétrique) par rapport à l’axe de symétrie. Cela signifie que les coordonnées y des points directement en travers de l'axe de symétrie seront les mêmes. Les coordonnées y pour les coordonnées x -2 et +2 sont toutes les deux 7; les coordonnées y pour les coordonnées x -1 et +1 sont toutes les deux 1, etc.
7 Insérez les valeurs calculées de y dans la table. Maintenant que vous avez trouvé au moins cinq paires de coordonnées pour la parabole, vous êtes presque prêt à le représenter graphiquement. Sur la base de votre travail, vous avez maintenant les points suivants: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Rappelez-vous que la parabole est réfléchie (symétrique) par rapport à l’axe de symétrie. Cela signifie que les coordonnées y des points directement en travers de l'axe de symétrie seront les mêmes. Les coordonnées y pour les coordonnées x -2 et +2 sont toutes les deux 7; les coordonnées y pour les coordonnées x -1 et +1 sont toutes les deux 1, etc. -
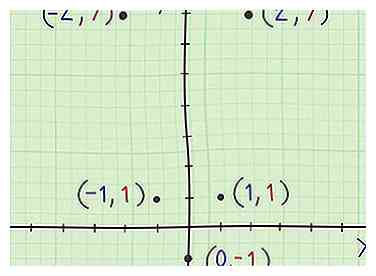 8 Tracez les points de la table sur le plan de coordonnées. Chaque ligne de la table forme une paire de coordonnées (x, y) sur le plan de coordonnées. Tracez tous les points en utilisant les coordonnées données dans le tableau.
8 Tracez les points de la table sur le plan de coordonnées. Chaque ligne de la table forme une paire de coordonnées (x, y) sur le plan de coordonnées. Tracez tous les points en utilisant les coordonnées données dans le tableau. - L'axe des x est horizontal; l'axe des y est vertical.
- Les nombres positifs sur l'axe des y sont au-dessus du point (0, 0) et les nombres négatifs sur l'axe des y sont inférieurs au point (0, 0).
- Les nombres positifs sur l'axe des x sont à droite du point (0, 0) et les nombres négatifs sur l'axe des x sont à gauche du point (0, 0).
-
 9 Connectez les points. Pour représenter graphiquement la parabole, connectez les points indiqués à l'étape précédente. Le graphique dans cet exemple ressemblera à un U. Connectez les points en utilisant des lignes légèrement incurvées (plutôt que droites). Cela créera l'image la plus précise de la parabole (qui est au moins légèrement incurvée sur toute sa longueur). Aux deux extrémités de la parabole, vous pouvez dessiner des flèches qui s’éloignent du sommet si vous le souhaitez. Cela indiquera que la parabole se poursuit indéfiniment. [5]
9 Connectez les points. Pour représenter graphiquement la parabole, connectez les points indiqués à l'étape précédente. Le graphique dans cet exemple ressemblera à un U. Connectez les points en utilisant des lignes légèrement incurvées (plutôt que droites). Cela créera l'image la plus précise de la parabole (qui est au moins légèrement incurvée sur toute sa longueur). Aux deux extrémités de la parabole, vous pouvez dessiner des flèches qui s’éloignent du sommet si vous le souhaitez. Cela indiquera que la parabole se poursuit indéfiniment. [5]
Deuxième partie de deux:
Décalage du graphique d'une parabole
Si vous voulez un raccourci pour déplacer une parabole sans avoir à retrouver son sommet et à re-tracer plusieurs points, vous devez comprendre comment lire l'équation d'une parabole et apprendre à la décaler verticalement ou horizontalement. Commencez avec la parabole de base: y = x2. Cela a son sommet à (0, 0) et s'ouvre vers le haut. Les points incluent (-1, 1), (1, 1), (-2, 4) et (2, 4). Vous pouvez déplacer une parabole en fonction de son équation. [6]
-
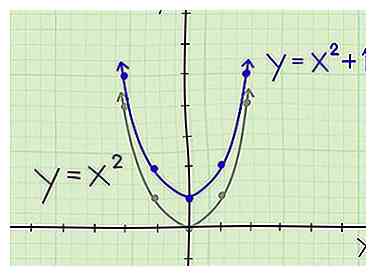 1 Décaler une parabole vers le haut. Considérez l'équation y = x2 +1. Cela déplace la parabole originale vers le haut d'une unité. Le sommet est maintenant (0, 1) au lieu de (0, 0). Il conservera la forme exacte de la parabole originale, mais chaque coordonnée y sera déplacée vers le haut d'une unité. Donc, au lieu de (-1, 1) et (1, 1), on trace (-1, 2) et (1, 2).
1 Décaler une parabole vers le haut. Considérez l'équation y = x2 +1. Cela déplace la parabole originale vers le haut d'une unité. Le sommet est maintenant (0, 1) au lieu de (0, 0). Il conservera la forme exacte de la parabole originale, mais chaque coordonnée y sera déplacée vers le haut d'une unité. Donc, au lieu de (-1, 1) et (1, 1), on trace (-1, 2) et (1, 2). -
 2 Décaler une parabole vers le bas. Prenez l'équation y = x2 -1. Nous décalons la parabole originale vers le bas de 1 unité, de sorte que le sommet est maintenant (0, -1) au lieu de (0, 0). Il aura toujours la même forme que la parabole originale, mais chaque coordonnée y sera décalée d'une unité vers le bas. Ainsi, au lieu de (-1, 1) et (1, 1), par exemple, on trace (-1, 0) et (1, 0).
2 Décaler une parabole vers le bas. Prenez l'équation y = x2 -1. Nous décalons la parabole originale vers le bas de 1 unité, de sorte que le sommet est maintenant (0, -1) au lieu de (0, 0). Il aura toujours la même forme que la parabole originale, mais chaque coordonnée y sera décalée d'une unité vers le bas. Ainsi, au lieu de (-1, 1) et (1, 1), par exemple, on trace (-1, 0) et (1, 0). -
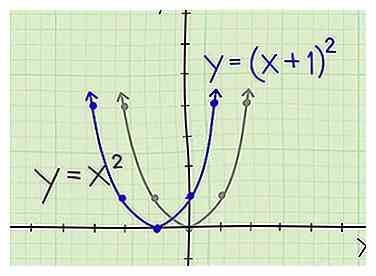 3 Déplacez une parabole vers la gauche. Considérez l'équation y = (x + 1)2. Cela déplace la parabole originale d'une unité vers la gauche. Le sommet est maintenant (-1, 0) au lieu de (0, 0). Il conserve la forme de la parabole d'origine, mais chaque coordonnée x est décalée vers la gauche. Au lieu de (-1, 1) et (1, 1), par exemple, on trace (-2, 1) et (0, 1).
3 Déplacez une parabole vers la gauche. Considérez l'équation y = (x + 1)2. Cela déplace la parabole originale d'une unité vers la gauche. Le sommet est maintenant (-1, 0) au lieu de (0, 0). Il conserve la forme de la parabole d'origine, mais chaque coordonnée x est décalée vers la gauche. Au lieu de (-1, 1) et (1, 1), par exemple, on trace (-2, 1) et (0, 1). -
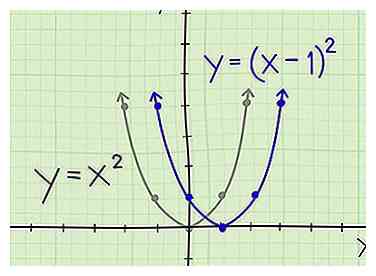 4 Déplacez une parabole vers la droite. Considérez l'équation y = (x - 1)2. C'est la parabole originale déplacée d'une unité vers la droite. Le sommet est maintenant (1, 0) au lieu de (0, 0). Il conserve la forme de la parabole originale, mais chaque coordonnée x sera déplacée vers la droite. Au lieu de (-1, 1) et (1, 1), par exemple, on trace (0, 1) et (2, 1).
4 Déplacez une parabole vers la droite. Considérez l'équation y = (x - 1)2. C'est la parabole originale déplacée d'une unité vers la droite. Le sommet est maintenant (1, 0) au lieu de (0, 0). Il conserve la forme de la parabole originale, mais chaque coordonnée x sera déplacée vers la droite. Au lieu de (-1, 1) et (1, 1), par exemple, on trace (0, 1) et (2, 1).
 Minotauromaquia
Minotauromaquia
 1 Comprendre les parties d'une parabole. Vous pouvez recevoir certaines informations avant de commencer et connaître la terminologie vous aidera à éviter les étapes inutiles. Voici les parties de la parabole à connaître: [1]
1 Comprendre les parties d'une parabole. Vous pouvez recevoir certaines informations avant de commencer et connaître la terminologie vous aidera à éviter les étapes inutiles. Voici les parties de la parabole à connaître: [1]  2 Connaître l'équation d'une parabole. L'équation générale d'une parabole est y = hache2+ bx + c. Il peut également être écrit sous la forme encore plus générale y = a (x - h) ² + k, mais nous allons nous concentrer ici sur la première forme de l’équation.
2 Connaître l'équation d'une parabole. L'équation générale d'une parabole est y = hache2+ bx + c. Il peut également être écrit sous la forme encore plus générale y = a (x - h) ² + k, mais nous allons nous concentrer ici sur la première forme de l’équation. 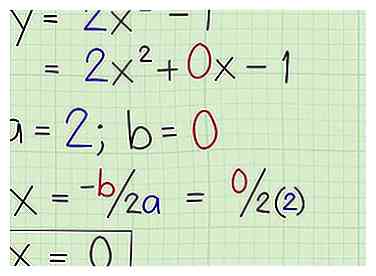 3 Trouvez l'axe de symétrie. Rappelez-vous que l'axe de symétrie est la ligne droite qui traverse le point tournant (sommet) de la parabole. Dans le cas d'une parabole verticale (ouverture ou descente), l'axe est identique à la coordonnée x du sommet, qui est la valeur x du point où l'axe de symétrie traverse la parabole. Pour trouver l'axe de symétrie, utilisez cette formule: x = -b / 2a. [3]
3 Trouvez l'axe de symétrie. Rappelez-vous que l'axe de symétrie est la ligne droite qui traverse le point tournant (sommet) de la parabole. Dans le cas d'une parabole verticale (ouverture ou descente), l'axe est identique à la coordonnée x du sommet, qui est la valeur x du point où l'axe de symétrie traverse la parabole. Pour trouver l'axe de symétrie, utilisez cette formule: x = -b / 2a. [3] 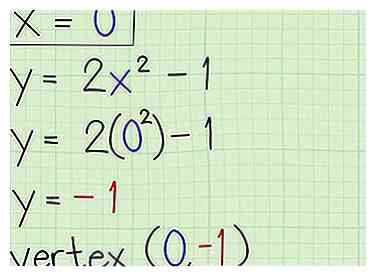 4 Trouvez le sommet. Une fois que vous connaissez l'axe de symétrie, vous pouvez brancher cette valeur pour que x obtienne la coordonnée y. Ces deux coordonnées vous donneront le sommet de la parabole. Dans ce cas, vous devez brancher 0 à 2x2 -1 pour obtenir la coordonnée y. y = 2 x 02 -1 = 0 -1 = -1. Le sommet est (0, -1) et la parabole traverse l'axe des y à -1. [4]
4 Trouvez le sommet. Une fois que vous connaissez l'axe de symétrie, vous pouvez brancher cette valeur pour que x obtienne la coordonnée y. Ces deux coordonnées vous donneront le sommet de la parabole. Dans ce cas, vous devez brancher 0 à 2x2 -1 pour obtenir la coordonnée y. y = 2 x 02 -1 = 0 -1 = -1. Le sommet est (0, -1) et la parabole traverse l'axe des y à -1. [4]  5 Configurez un tableau avec les valeurs choisies de x. Créez une table avec des valeurs particulières de x dans la première colonne. Ce tableau vous donnera les coordonnées dont vous avez besoin pour représenter l'équation.
5 Configurez un tableau avec les valeurs choisies de x. Créez une table avec des valeurs particulières de x dans la première colonne. Ce tableau vous donnera les coordonnées dont vous avez besoin pour représenter l'équation.  6 Calculez les valeurs des coordonnées y correspondantes. Remplacez chaque valeur de x dans l'équation de la parabole et calculez les valeurs correspondantes de y. Insérez ces valeurs calculées de y dans la table. Dans cet exemple, les valeurs de y sont calculées comme suit:
6 Calculez les valeurs des coordonnées y correspondantes. Remplacez chaque valeur de x dans l'équation de la parabole et calculez les valeurs correspondantes de y. Insérez ces valeurs calculées de y dans la table. Dans cet exemple, les valeurs de y sont calculées comme suit:  7 Insérez les valeurs calculées de y dans la table. Maintenant que vous avez trouvé au moins cinq paires de coordonnées pour la parabole, vous êtes presque prêt à le représenter graphiquement. Sur la base de votre travail, vous avez maintenant les points suivants: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Rappelez-vous que la parabole est réfléchie (symétrique) par rapport à l’axe de symétrie. Cela signifie que les coordonnées y des points directement en travers de l'axe de symétrie seront les mêmes. Les coordonnées y pour les coordonnées x -2 et +2 sont toutes les deux 7; les coordonnées y pour les coordonnées x -1 et +1 sont toutes les deux 1, etc.
7 Insérez les valeurs calculées de y dans la table. Maintenant que vous avez trouvé au moins cinq paires de coordonnées pour la parabole, vous êtes presque prêt à le représenter graphiquement. Sur la base de votre travail, vous avez maintenant les points suivants: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Rappelez-vous que la parabole est réfléchie (symétrique) par rapport à l’axe de symétrie. Cela signifie que les coordonnées y des points directement en travers de l'axe de symétrie seront les mêmes. Les coordonnées y pour les coordonnées x -2 et +2 sont toutes les deux 7; les coordonnées y pour les coordonnées x -1 et +1 sont toutes les deux 1, etc.  8 Tracez les points de la table sur le plan de coordonnées. Chaque ligne de la table forme une paire de coordonnées (x, y) sur le plan de coordonnées. Tracez tous les points en utilisant les coordonnées données dans le tableau.
8 Tracez les points de la table sur le plan de coordonnées. Chaque ligne de la table forme une paire de coordonnées (x, y) sur le plan de coordonnées. Tracez tous les points en utilisant les coordonnées données dans le tableau.  9 Connectez les points. Pour représenter graphiquement la parabole, connectez les points indiqués à l'étape précédente. Le graphique dans cet exemple ressemblera à un U. Connectez les points en utilisant des lignes légèrement incurvées (plutôt que droites). Cela créera l'image la plus précise de la parabole (qui est au moins légèrement incurvée sur toute sa longueur). Aux deux extrémités de la parabole, vous pouvez dessiner des flèches qui s’éloignent du sommet si vous le souhaitez. Cela indiquera que la parabole se poursuit indéfiniment. [5]
9 Connectez les points. Pour représenter graphiquement la parabole, connectez les points indiqués à l'étape précédente. Le graphique dans cet exemple ressemblera à un U. Connectez les points en utilisant des lignes légèrement incurvées (plutôt que droites). Cela créera l'image la plus précise de la parabole (qui est au moins légèrement incurvée sur toute sa longueur). Aux deux extrémités de la parabole, vous pouvez dessiner des flèches qui s’éloignent du sommet si vous le souhaitez. Cela indiquera que la parabole se poursuit indéfiniment. [5]  1 Décaler une parabole vers le haut. Considérez l'équation y = x2 +1. Cela déplace la parabole originale vers le haut d'une unité. Le sommet est maintenant (0, 1) au lieu de (0, 0). Il conservera la forme exacte de la parabole originale, mais chaque coordonnée y sera déplacée vers le haut d'une unité. Donc, au lieu de (-1, 1) et (1, 1), on trace (-1, 2) et (1, 2).
1 Décaler une parabole vers le haut. Considérez l'équation y = x2 +1. Cela déplace la parabole originale vers le haut d'une unité. Le sommet est maintenant (0, 1) au lieu de (0, 0). Il conservera la forme exacte de la parabole originale, mais chaque coordonnée y sera déplacée vers le haut d'une unité. Donc, au lieu de (-1, 1) et (1, 1), on trace (-1, 2) et (1, 2).  2 Décaler une parabole vers le bas. Prenez l'équation y = x2 -1. Nous décalons la parabole originale vers le bas de 1 unité, de sorte que le sommet est maintenant (0, -1) au lieu de (0, 0). Il aura toujours la même forme que la parabole originale, mais chaque coordonnée y sera décalée d'une unité vers le bas. Ainsi, au lieu de (-1, 1) et (1, 1), par exemple, on trace (-1, 0) et (1, 0).
2 Décaler une parabole vers le bas. Prenez l'équation y = x2 -1. Nous décalons la parabole originale vers le bas de 1 unité, de sorte que le sommet est maintenant (0, -1) au lieu de (0, 0). Il aura toujours la même forme que la parabole originale, mais chaque coordonnée y sera décalée d'une unité vers le bas. Ainsi, au lieu de (-1, 1) et (1, 1), par exemple, on trace (-1, 0) et (1, 0).  3 Déplacez une parabole vers la gauche. Considérez l'équation y = (x + 1)2. Cela déplace la parabole originale d'une unité vers la gauche. Le sommet est maintenant (-1, 0) au lieu de (0, 0). Il conserve la forme de la parabole d'origine, mais chaque coordonnée x est décalée vers la gauche. Au lieu de (-1, 1) et (1, 1), par exemple, on trace (-2, 1) et (0, 1).
3 Déplacez une parabole vers la gauche. Considérez l'équation y = (x + 1)2. Cela déplace la parabole originale d'une unité vers la gauche. Le sommet est maintenant (-1, 0) au lieu de (0, 0). Il conserve la forme de la parabole d'origine, mais chaque coordonnée x est décalée vers la gauche. Au lieu de (-1, 1) et (1, 1), par exemple, on trace (-2, 1) et (0, 1).  4 Déplacez une parabole vers la droite. Considérez l'équation y = (x - 1)2. C'est la parabole originale déplacée d'une unité vers la droite. Le sommet est maintenant (1, 0) au lieu de (0, 0). Il conserve la forme de la parabole originale, mais chaque coordonnée x sera déplacée vers la droite. Au lieu de (-1, 1) et (1, 1), par exemple, on trace (0, 1) et (2, 1).
4 Déplacez une parabole vers la droite. Considérez l'équation y = (x - 1)2. C'est la parabole originale déplacée d'une unité vers la droite. Le sommet est maintenant (1, 0) au lieu de (0, 0). Il conserve la forme de la parabole originale, mais chaque coordonnée x sera déplacée vers la droite. Au lieu de (-1, 1) et (1, 1), par exemple, on trace (0, 1) et (2, 1).