Une fonction rationnelle est une équation qui prend la forme y = N (X)/RÉ(X) où N et D sont des polynômes. Tenter d'esquisser un graphique précis d'un à la main peut être une revue complète de nombreux sujets mathématiques parmi les plus importants, de l'algèbre de base au calcul différentiel. Prenons l'exemple suivant: y = (2X2 - 6X + 5)/(4X + 2).
Pas
-
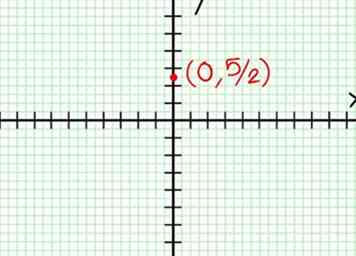 1 Trouvez le y intercepter. Définissez simplement X = 0. Tout sauf les termes constants disparaissent, laissant y = 5/2. L'exprimer comme une paire de coordonnées (0, 5/2) est un point du graphique. Graphique ce point.
1 Trouvez le y intercepter. Définissez simplement X = 0. Tout sauf les termes constants disparaissent, laissant y = 5/2. L'exprimer comme une paire de coordonnées (0, 5/2) est un point du graphique. Graphique ce point. -
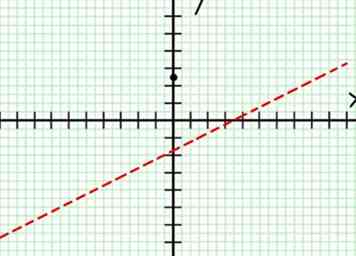 2 Trouvez l'asymptote horizontale. Divisez le dénominateur en numérateur pour déterminer le comportement de y pour de grandes valeurs absolues de X. Dans cet exemple, la division montre que y = (1/2)X - (7/4) + 17/(8X + 4). Pour les grandes valeurs positives ou négatives de x, 17 / (8X + 4) s'approche de zéro et le graphique se rapproche de la ligne y = (1/2)X - (7/4). En utilisant une ligne pointillée ou légèrement dessinée, tracez cette ligne.
2 Trouvez l'asymptote horizontale. Divisez le dénominateur en numérateur pour déterminer le comportement de y pour de grandes valeurs absolues de X. Dans cet exemple, la division montre que y = (1/2)X - (7/4) + 17/(8X + 4). Pour les grandes valeurs positives ou négatives de x, 17 / (8X + 4) s'approche de zéro et le graphique se rapproche de la ligne y = (1/2)X - (7/4). En utilisant une ligne pointillée ou légèrement dessinée, tracez cette ligne. - Si le degré du numérateur est inférieur au degré du dénominateur, il n'y a pas de division à faire et l'asymptote est y = 0.
- Si deg (N) = deg (D), l'asymptote est une ligne horizontale au rapport des coefficients principaux.
- Si deg (N) = deg (D) + 1, l'asymptote est une ligne dont la pente est le rapport des coefficients principaux.
- Si deg (N)> deg (D) + 1, alors pour les grandes valeurs de |X|, y passe rapidement à l'infini positif ou négatif sous la forme d'un polynôme quadratique, cubique ou supérieur. Dans ce cas, il ne vaut probablement pas la peine de représenter avec précision le quotient de la division.
-
 3 Trouvez les zéros. Une fonction rationnelle a un zéro quand son numérateur est zéro, donc mettez N (X) = 0. Dans l'exemple, 2X2 - 6X + 5 = 0. Le discriminant de ce quadratique est b2 - 4ac = 62 - 4 * 2 * 5 = 36 - 40 = -4. Puisque le discriminant est négatif, N (X), et par conséquent f (X), n'a pas de vraies racines. Le graphique ne traverse jamais le X-axe. Si des zéros ont été trouvés, ajoutez ces points au graphique.
3 Trouvez les zéros. Une fonction rationnelle a un zéro quand son numérateur est zéro, donc mettez N (X) = 0. Dans l'exemple, 2X2 - 6X + 5 = 0. Le discriminant de ce quadratique est b2 - 4ac = 62 - 4 * 2 * 5 = 36 - 40 = -4. Puisque le discriminant est négatif, N (X), et par conséquent f (X), n'a pas de vraies racines. Le graphique ne traverse jamais le X-axe. Si des zéros ont été trouvés, ajoutez ces points au graphique. -
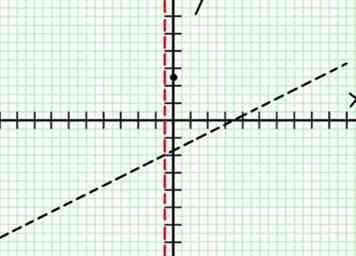 4 Trouvez les asymptotes verticales. Une asymptote verticale se produit lorsque le dénominateur est zéro. Réglage 4X + 2 = 0 donne la ligne verticale X = -1/2. Représentez graphiquement chaque asymptote verticale avec une ligne claire ou en pointillé. Si une certaine valeur de X fait les deux N (X) = 0 et D (X) = 0, il peut y avoir ou non une asymptote verticale. C'est rare, mais consultez les conseils pour y faire face si cela se produit.
4 Trouvez les asymptotes verticales. Une asymptote verticale se produit lorsque le dénominateur est zéro. Réglage 4X + 2 = 0 donne la ligne verticale X = -1/2. Représentez graphiquement chaque asymptote verticale avec une ligne claire ou en pointillé. Si une certaine valeur de X fait les deux N (X) = 0 et D (X) = 0, il peut y avoir ou non une asymptote verticale. C'est rare, mais consultez les conseils pour y faire face si cela se produit. -
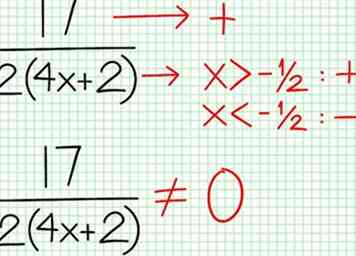 5 Regardez le reste de la division à l'étape 2. Quand est-ce positif, négatif ou nul? Dans l'exemple, le numérateur du reste est 17, ce qui est toujours positif. Le dénominateur, 4X + 2, est positif à droite de l'asymptote verticale et négatif à gauche. Cela signifie que le graphique se rapproche de l’asymptote linéaire de ce qui précède pour les grandes valeurs positives de X et d'en bas pour les grandes valeurs négatives de X. Depuis 17 / (8X + 4) ne peut jamais être nul, ce graphe ne coupe jamais la ligne y = (1/2)X - (7/4). N'ajoutez rien au graphique maintenant, mais notez ces conclusions pour plus tard.
5 Regardez le reste de la division à l'étape 2. Quand est-ce positif, négatif ou nul? Dans l'exemple, le numérateur du reste est 17, ce qui est toujours positif. Le dénominateur, 4X + 2, est positif à droite de l'asymptote verticale et négatif à gauche. Cela signifie que le graphique se rapproche de l’asymptote linéaire de ce qui précède pour les grandes valeurs positives de X et d'en bas pour les grandes valeurs négatives de X. Depuis 17 / (8X + 4) ne peut jamais être nul, ce graphe ne coupe jamais la ligne y = (1/2)X - (7/4). N'ajoutez rien au graphique maintenant, mais notez ces conclusions pour plus tard. -
 6 Trouvez les extrema locaux. Un extremum local peut apparaître chaque fois que N '(X)RÉ(X) - N (X)RÉ'(X) = 0. Dans l'exemple, N '(X) = 4X - 6 et D '(X) = 4. N '(X)RÉ(X) - N (X)RÉ'(X) = (4X - 6)(4X + 2) - (2X2 - 6X + 5) * 4 = 0. Expansion, combinaison des termes et division par 4 feuilles X2 + X - 4 = 0. La formule quadratique montre des racines proches X = 3/2 et X = -5/2. (Celles-ci diffèrent d'environ 0,06 par rapport aux valeurs exactes, mais notre graphique ne sera pas assez précis pour s'inquiéter de ce niveau de détail. Le choix d'une approximation rationnelle décente rend l'étape suivante plus facile.)
6 Trouvez les extrema locaux. Un extremum local peut apparaître chaque fois que N '(X)RÉ(X) - N (X)RÉ'(X) = 0. Dans l'exemple, N '(X) = 4X - 6 et D '(X) = 4. N '(X)RÉ(X) - N (X)RÉ'(X) = (4X - 6)(4X + 2) - (2X2 - 6X + 5) * 4 = 0. Expansion, combinaison des termes et division par 4 feuilles X2 + X - 4 = 0. La formule quadratique montre des racines proches X = 3/2 et X = -5/2. (Celles-ci diffèrent d'environ 0,06 par rapport aux valeurs exactes, mais notre graphique ne sera pas assez précis pour s'inquiéter de ce niveau de détail. Le choix d'une approximation rationnelle décente rend l'étape suivante plus facile.) -
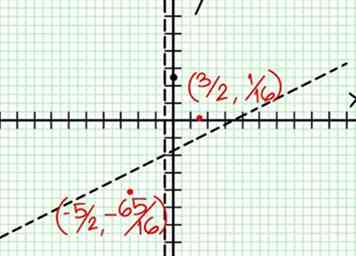 7 Trouvez le y-valeurs de chaque extremum local. Branchez le X-valeurs de la précédente étape dans la fonction rationnelle d'origine pour trouver le correspondant y-valeurs. Dans l'exemple, f (3/2) = 1/16 et f (-5/2) = -65/16. Ajoutez ces points (3/2, 1/16) et (-5/2, -65/16) au graphique. Puisque nous nous sommes approchés à l'étape précédente, ce ne sont pas les minima et les maxima exacts, mais ils sont probablement proches. (Nous savons (3/2, 1/16) est très proche du minimum local. À partir de l'étape 3, nous savons que y est toujours positif quand X > -1/2 et nous avons trouvé une valeur aussi petite que 1/16, donc au moins dans ce cas, l'erreur est probablement inférieure à l'épaisseur de la ligne.)
7 Trouvez le y-valeurs de chaque extremum local. Branchez le X-valeurs de la précédente étape dans la fonction rationnelle d'origine pour trouver le correspondant y-valeurs. Dans l'exemple, f (3/2) = 1/16 et f (-5/2) = -65/16. Ajoutez ces points (3/2, 1/16) et (-5/2, -65/16) au graphique. Puisque nous nous sommes approchés à l'étape précédente, ce ne sont pas les minima et les maxima exacts, mais ils sont probablement proches. (Nous savons (3/2, 1/16) est très proche du minimum local. À partir de l'étape 3, nous savons que y est toujours positif quand X > -1/2 et nous avons trouvé une valeur aussi petite que 1/16, donc au moins dans ce cas, l'erreur est probablement inférieure à l'épaisseur de la ligne.) -
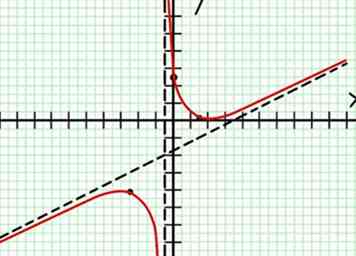 8 Relier les points et étendre doucement le graphique des points connus aux asymptotes en prenant soin de les approcher de la bonne direction. Veillez à ne pas franchir la X-axis sauf aux points déjà trouvés à l'étape 3. Ne traversez pas l'asymptote horizontale ou linéaire sauf aux points déjà trouvés à l'étape 5. Ne passez pas de la pente ascendante à la pente descendante sauf à l'extrême trouvé à l'étape précédente .
8 Relier les points et étendre doucement le graphique des points connus aux asymptotes en prenant soin de les approcher de la bonne direction. Veillez à ne pas franchir la X-axis sauf aux points déjà trouvés à l'étape 3. Ne traversez pas l'asymptote horizontale ou linéaire sauf aux points déjà trouvés à l'étape 5. Ne passez pas de la pente ascendante à la pente descendante sauf à l'extrême trouvé à l'étape précédente .
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Trouvez le y intercepter. Définissez simplement X = 0. Tout sauf les termes constants disparaissent, laissant y = 5/2. L'exprimer comme une paire de coordonnées (0, 5/2) est un point du graphique. Graphique ce point.
1 Trouvez le y intercepter. Définissez simplement X = 0. Tout sauf les termes constants disparaissent, laissant y = 5/2. L'exprimer comme une paire de coordonnées (0, 5/2) est un point du graphique. Graphique ce point.  2 Trouvez l'asymptote horizontale. Divisez le dénominateur en numérateur pour déterminer le comportement de y pour de grandes valeurs absolues de X. Dans cet exemple, la division montre que y = (1/2)X - (7/4) + 17/(8X + 4). Pour les grandes valeurs positives ou négatives de x, 17 / (8X + 4) s'approche de zéro et le graphique se rapproche de la ligne y = (1/2)X - (7/4). En utilisant une ligne pointillée ou légèrement dessinée, tracez cette ligne.
2 Trouvez l'asymptote horizontale. Divisez le dénominateur en numérateur pour déterminer le comportement de y pour de grandes valeurs absolues de X. Dans cet exemple, la division montre que y = (1/2)X - (7/4) + 17/(8X + 4). Pour les grandes valeurs positives ou négatives de x, 17 / (8X + 4) s'approche de zéro et le graphique se rapproche de la ligne y = (1/2)X - (7/4). En utilisant une ligne pointillée ou légèrement dessinée, tracez cette ligne.  3 Trouvez les zéros. Une fonction rationnelle a un zéro quand son numérateur est zéro, donc mettez N (X) = 0. Dans l'exemple, 2X2 - 6X + 5 = 0. Le discriminant de ce quadratique est b2 - 4ac = 62 - 4 * 2 * 5 = 36 - 40 = -4. Puisque le discriminant est négatif, N (X), et par conséquent f (X), n'a pas de vraies racines. Le graphique ne traverse jamais le X-axe. Si des zéros ont été trouvés, ajoutez ces points au graphique.
3 Trouvez les zéros. Une fonction rationnelle a un zéro quand son numérateur est zéro, donc mettez N (X) = 0. Dans l'exemple, 2X2 - 6X + 5 = 0. Le discriminant de ce quadratique est b2 - 4ac = 62 - 4 * 2 * 5 = 36 - 40 = -4. Puisque le discriminant est négatif, N (X), et par conséquent f (X), n'a pas de vraies racines. Le graphique ne traverse jamais le X-axe. Si des zéros ont été trouvés, ajoutez ces points au graphique.  4 Trouvez les asymptotes verticales. Une asymptote verticale se produit lorsque le dénominateur est zéro. Réglage 4X + 2 = 0 donne la ligne verticale X = -1/2. Représentez graphiquement chaque asymptote verticale avec une ligne claire ou en pointillé. Si une certaine valeur de X fait les deux N (X) = 0 et D (X) = 0, il peut y avoir ou non une asymptote verticale. C'est rare, mais consultez les conseils pour y faire face si cela se produit.
4 Trouvez les asymptotes verticales. Une asymptote verticale se produit lorsque le dénominateur est zéro. Réglage 4X + 2 = 0 donne la ligne verticale X = -1/2. Représentez graphiquement chaque asymptote verticale avec une ligne claire ou en pointillé. Si une certaine valeur de X fait les deux N (X) = 0 et D (X) = 0, il peut y avoir ou non une asymptote verticale. C'est rare, mais consultez les conseils pour y faire face si cela se produit. 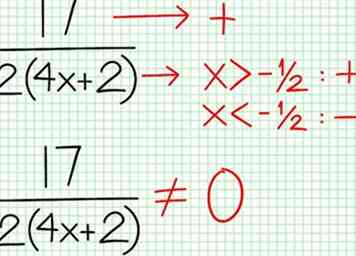 5 Regardez le reste de la division à l'étape 2. Quand est-ce positif, négatif ou nul? Dans l'exemple, le numérateur du reste est 17, ce qui est toujours positif. Le dénominateur, 4X + 2, est positif à droite de l'asymptote verticale et négatif à gauche. Cela signifie que le graphique se rapproche de l’asymptote linéaire de ce qui précède pour les grandes valeurs positives de X et d'en bas pour les grandes valeurs négatives de X. Depuis 17 / (8X + 4) ne peut jamais être nul, ce graphe ne coupe jamais la ligne y = (1/2)X - (7/4). N'ajoutez rien au graphique maintenant, mais notez ces conclusions pour plus tard.
5 Regardez le reste de la division à l'étape 2. Quand est-ce positif, négatif ou nul? Dans l'exemple, le numérateur du reste est 17, ce qui est toujours positif. Le dénominateur, 4X + 2, est positif à droite de l'asymptote verticale et négatif à gauche. Cela signifie que le graphique se rapproche de l’asymptote linéaire de ce qui précède pour les grandes valeurs positives de X et d'en bas pour les grandes valeurs négatives de X. Depuis 17 / (8X + 4) ne peut jamais être nul, ce graphe ne coupe jamais la ligne y = (1/2)X - (7/4). N'ajoutez rien au graphique maintenant, mais notez ces conclusions pour plus tard.  6 Trouvez les extrema locaux. Un extremum local peut apparaître chaque fois que N '(X)RÉ(X) - N (X)RÉ'(X) = 0. Dans l'exemple, N '(X) = 4X - 6 et D '(X) = 4. N '(X)RÉ(X) - N (X)RÉ'(X) = (4X - 6)(4X + 2) - (2X2 - 6X + 5) * 4 = 0. Expansion, combinaison des termes et division par 4 feuilles X2 + X - 4 = 0. La formule quadratique montre des racines proches X = 3/2 et X = -5/2. (Celles-ci diffèrent d'environ 0,06 par rapport aux valeurs exactes, mais notre graphique ne sera pas assez précis pour s'inquiéter de ce niveau de détail. Le choix d'une approximation rationnelle décente rend l'étape suivante plus facile.)
6 Trouvez les extrema locaux. Un extremum local peut apparaître chaque fois que N '(X)RÉ(X) - N (X)RÉ'(X) = 0. Dans l'exemple, N '(X) = 4X - 6 et D '(X) = 4. N '(X)RÉ(X) - N (X)RÉ'(X) = (4X - 6)(4X + 2) - (2X2 - 6X + 5) * 4 = 0. Expansion, combinaison des termes et division par 4 feuilles X2 + X - 4 = 0. La formule quadratique montre des racines proches X = 3/2 et X = -5/2. (Celles-ci diffèrent d'environ 0,06 par rapport aux valeurs exactes, mais notre graphique ne sera pas assez précis pour s'inquiéter de ce niveau de détail. Le choix d'une approximation rationnelle décente rend l'étape suivante plus facile.)  7 Trouvez le y-valeurs de chaque extremum local. Branchez le X-valeurs de la précédente étape dans la fonction rationnelle d'origine pour trouver le correspondant y-valeurs. Dans l'exemple, f (3/2) = 1/16 et f (-5/2) = -65/16. Ajoutez ces points (3/2, 1/16) et (-5/2, -65/16) au graphique. Puisque nous nous sommes approchés à l'étape précédente, ce ne sont pas les minima et les maxima exacts, mais ils sont probablement proches. (Nous savons (3/2, 1/16) est très proche du minimum local. À partir de l'étape 3, nous savons que y est toujours positif quand X > -1/2 et nous avons trouvé une valeur aussi petite que 1/16, donc au moins dans ce cas, l'erreur est probablement inférieure à l'épaisseur de la ligne.)
7 Trouvez le y-valeurs de chaque extremum local. Branchez le X-valeurs de la précédente étape dans la fonction rationnelle d'origine pour trouver le correspondant y-valeurs. Dans l'exemple, f (3/2) = 1/16 et f (-5/2) = -65/16. Ajoutez ces points (3/2, 1/16) et (-5/2, -65/16) au graphique. Puisque nous nous sommes approchés à l'étape précédente, ce ne sont pas les minima et les maxima exacts, mais ils sont probablement proches. (Nous savons (3/2, 1/16) est très proche du minimum local. À partir de l'étape 3, nous savons que y est toujours positif quand X > -1/2 et nous avons trouvé une valeur aussi petite que 1/16, donc au moins dans ce cas, l'erreur est probablement inférieure à l'épaisseur de la ligne.)  8 Relier les points et étendre doucement le graphique des points connus aux asymptotes en prenant soin de les approcher de la bonne direction. Veillez à ne pas franchir la X-axis sauf aux points déjà trouvés à l'étape 3. Ne traversez pas l'asymptote horizontale ou linéaire sauf aux points déjà trouvés à l'étape 5. Ne passez pas de la pente ascendante à la pente descendante sauf à l'extrême trouvé à l'étape précédente .
8 Relier les points et étendre doucement le graphique des points connus aux asymptotes en prenant soin de les approcher de la bonne direction. Veillez à ne pas franchir la X-axis sauf aux points déjà trouvés à l'étape 3. Ne traversez pas l'asymptote horizontale ou linéaire sauf aux points déjà trouvés à l'étape 5. Ne passez pas de la pente ascendante à la pente descendante sauf à l'extrême trouvé à l'étape précédente .