Pour représenter graphiquement des points sur le plan de coordonnées, vous devez comprendre l'organisation du plan de coordonnées et savoir quoi faire avec ces coordonnées (x, y). Si vous voulez savoir comment représenter graphiquement des points sur le plan de coordonnées, suivez ces étapes.
Première partie de trois:
Comprendre le plan de coordonnées
-
 1 Comprendre les axes du plan de coordonnées. Lorsque vous tracez un point sur le plan de coordonnées, vous le tracez sous la forme (x, y). Voici ce que vous devez savoir:
1 Comprendre les axes du plan de coordonnées. Lorsque vous tracez un point sur le plan de coordonnées, vous le tracez sous la forme (x, y). Voici ce que vous devez savoir: - L'axe des x va à gauche et à droite, la deuxième coordonnée est sur l'axe des y.
- L'axe des y monte et descend.
- Les nombres positifs montent ou descendent (selon l'axe). Les nombres négatifs vont à gauche ou à droite.
-
 2 Comprendre les quadrants sur le plan de coordonnées. Rappelez-vous qu'un graphique a quatre quadrants (généralement étiquetés en chiffres romains). Vous devrez savoir dans quel quadrant l'avion se trouve.
2 Comprendre les quadrants sur le plan de coordonnées. Rappelez-vous qu'un graphique a quatre quadrants (généralement étiquetés en chiffres romains). Vous devrez savoir dans quel quadrant l'avion se trouve. - Le quadrant I (+, +); le quadrant I est au-dessus et à gauche de l'axe des y.
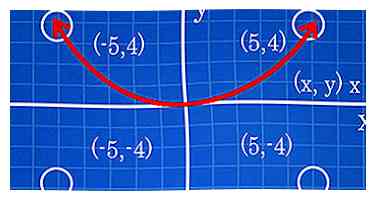
- Le quadrant IV devient (+, -); le quadrant IV est situé en dessous de l'axe des x et à droite de l'axe des y. (5,4) est dans le quadrant I.
- (-5,4) est dans le quadrant II. (-5, -4) est dans le quadrant III. (5, -4) est dans le quadrant IV.
Deuxième partie de trois:
Représentation graphique d'un point unique
-
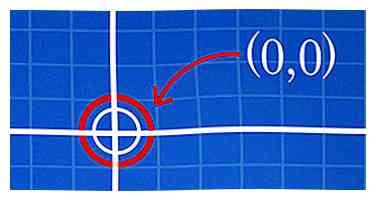 1 Commencez à (0, 0) ou l'origine. Il suffit d'aller à (0, 0), qui correspond à l'intersection des axes x et y, au centre du plan de coordonnées.[1]
1 Commencez à (0, 0) ou l'origine. Il suffit d'aller à (0, 0), qui correspond à l'intersection des axes x et y, au centre du plan de coordonnées.[1] -
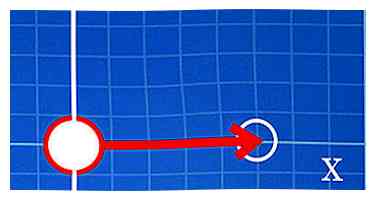 2 Déplacez-vous sur x unités à droite ou à gauche. Disons que vous travaillez avec le jeu de coordonnées (5, -4). Votre coordonnée x est 5. Puisque cinq est positif, vous devrez déplacer cinq unités vers la droite. Si c'était négatif, vous vous déplaceriez de plus de 5 unités vers la gauche.
2 Déplacez-vous sur x unités à droite ou à gauche. Disons que vous travaillez avec le jeu de coordonnées (5, -4). Votre coordonnée x est 5. Puisque cinq est positif, vous devrez déplacer cinq unités vers la droite. Si c'était négatif, vous vous déplaceriez de plus de 5 unités vers la gauche. -
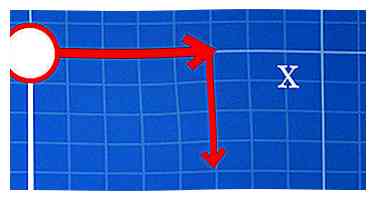 3 Déplacez-vous sur y unités vers le haut ou le bas. Commencez là où vous l'avez laissé, 5 unités à droite de (0, 0). Puisque votre coordonnée y est de -4, vous devrez descendre de quatre unités. Si c'était 4, vous monteriez de quatre unités.
3 Déplacez-vous sur y unités vers le haut ou le bas. Commencez là où vous l'avez laissé, 5 unités à droite de (0, 0). Puisque votre coordonnée y est de -4, vous devrez descendre de quatre unités. Si c'était 4, vous monteriez de quatre unités. -
 4 Marquez le point. Marquez le point que vous avez trouvé en vous déplaçant de 5 unités vers la droite et de 4 unités vers le bas, le point (5, -4), situé dans le 4ème quadrant. Vous avez tous terminé.
4 Marquez le point. Marquez le point que vous avez trouvé en vous déplaçant de 5 unités vers la droite et de 4 unités vers le bas, le point (5, -4), situé dans le 4ème quadrant. Vous avez tous terminé.
Troisième partie de trois:
Suivre des techniques avancées
-
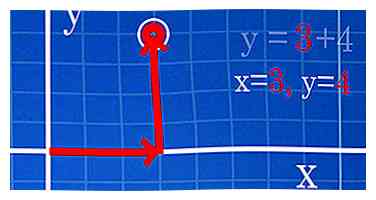 1 Apprenez à représenter graphiquement des points si vous travaillez avec une équation. Si vous avez une formule sans aucune coordonnée, vous devrez alors trouver vos points en choisissant une coordonnée aléatoire pour x et en voyant ce que la formule crache pour y. Continuez jusqu'à ce que vous ayez trouvé suffisamment de points et que vous puissiez tous les tracer, en les connectant si nécessaire. Voici comment vous pouvez le faire, que vous travailliez avec une simple ligne ou avec une équation plus compliquée telle qu'une parabole:
1 Apprenez à représenter graphiquement des points si vous travaillez avec une équation. Si vous avez une formule sans aucune coordonnée, vous devrez alors trouver vos points en choisissant une coordonnée aléatoire pour x et en voyant ce que la formule crache pour y. Continuez jusqu'à ce que vous ayez trouvé suffisamment de points et que vous puissiez tous les tracer, en les connectant si nécessaire. Voici comment vous pouvez le faire, que vous travailliez avec une simple ligne ou avec une équation plus compliquée telle qu'une parabole: - Points graphiques d'une ligne. Disons que l'équation est y = x + 4. Alors, choisissez un nombre aléatoire pour x, comme 3, et voyez ce que vous obtenez pour y. y = 3 + 4 = 7, vous avez donc trouvé le point (3, 7).
- Points graphiques à partir d'une équation quadratique. Disons que l'équation de la parabole est y = x2 + 2. Faites la même chose: choisissez un nombre aléatoire pour x et voyez ce que vous obtenez pour y. Choisir 0 pour x est le plus facile. y = 02 + 2, alors y = 2. Vous avez trouvé le point (0, 2).
-
 2 Connectez les points si nécessaire. Si vous devez créer un graphique linéaire, dessiner un cercle ou relier tous les points d'une parabole ou d'une autre équation quadratique, vous devrez connecter les points. Si vous avez une équation linéaire, dessinez des lignes reliant les points de gauche à droite. Si vous travaillez avec une équation quadratique, connectez les points avec des lignes courbes.
2 Connectez les points si nécessaire. Si vous devez créer un graphique linéaire, dessiner un cercle ou relier tous les points d'une parabole ou d'une autre équation quadratique, vous devrez connecter les points. Si vous avez une équation linéaire, dessinez des lignes reliant les points de gauche à droite. Si vous travaillez avec une équation quadratique, connectez les points avec des lignes courbes. - À moins de représenter graphiquement un point, vous aurez besoin d'au moins deux points. Une ligne nécessite deux points.
- Un cercle nécessite deux points si l'on est le centre; trois si le centre n'est pas inclus (sauf si l'instructeur a inclus le centre du cercle dans le problème, utilisez trois).
- Une parabole nécessite trois points, l’un étant le minimum ou le maximum absolu; les deux autres points doivent être opposés.
- Une hyperbole nécessite six points; trois sur chaque axe.
-
 3 Comprendre comment la modification de l’équation modifie le graphique. Voici les différentes manières dont la modification de l’équation modifie le graphique:
3 Comprendre comment la modification de l’équation modifie le graphique. Voici les différentes manières dont la modification de l’équation modifie le graphique: - La modification de la coordonnée x déplace l'équation vers la gauche ou la droite.
- L'ajout d'une constante déplace l'équation vers le haut ou le bas.
- Le tourner en négatif (en multipliant par -1) le retourne; Si c'est une ligne, ça va changer de monter ou descendre.
- Le multiplier par un autre nombre augmentera ou diminuera la pente.
-
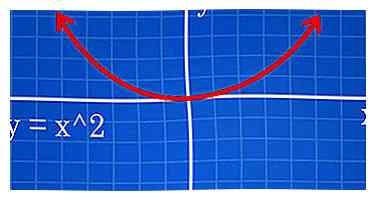 4 Suivez un exemple pour voir comment modifier l'équation modifie le graphique. Considérons l’équation y = x ^ 2; une parabole avec sa base à (0,0). Voici les différences que vous verrez en modifiant l'équation:
4 Suivez un exemple pour voir comment modifier l'équation modifie le graphique. Considérons l’équation y = x ^ 2; une parabole avec sa base à (0,0). Voici les différences que vous verrez en modifiant l'équation: - y = (x-2) ^ 2 est la même parabole, sauf qu'il est représenté graphiquement par deux espaces à droite de l'origine; sa base est maintenant à (2,0).
- y = x ^ 2 + 2 est toujours la même parabole, sauf que maintenant il est représenté graphiquement par deux espaces plus élevés à (0,2).
- y = -x ^ 2 (le négatif est appliqué après l'exposant ^ 2) est à l'envers y = x ^ 2; sa base est (0,0).
- y = 5x ^ 2 est toujours une parabole, mais elle grossit encore plus vite, ce qui lui donne un aspect plus fin.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Comprendre les axes du plan de coordonnées. Lorsque vous tracez un point sur le plan de coordonnées, vous le tracez sous la forme (x, y). Voici ce que vous devez savoir:
1 Comprendre les axes du plan de coordonnées. Lorsque vous tracez un point sur le plan de coordonnées, vous le tracez sous la forme (x, y). Voici ce que vous devez savoir:  2 Comprendre les quadrants sur le plan de coordonnées. Rappelez-vous qu'un graphique a quatre quadrants (généralement étiquetés en chiffres romains). Vous devrez savoir dans quel quadrant l'avion se trouve.
2 Comprendre les quadrants sur le plan de coordonnées. Rappelez-vous qu'un graphique a quatre quadrants (généralement étiquetés en chiffres romains). Vous devrez savoir dans quel quadrant l'avion se trouve.  1 Commencez à (0, 0) ou l'origine. Il suffit d'aller à (0, 0), qui correspond à l'intersection des axes x et y, au centre du plan de coordonnées.[1]
1 Commencez à (0, 0) ou l'origine. Il suffit d'aller à (0, 0), qui correspond à l'intersection des axes x et y, au centre du plan de coordonnées.[1]  2 Déplacez-vous sur x unités à droite ou à gauche. Disons que vous travaillez avec le jeu de coordonnées (5, -4). Votre coordonnée x est 5. Puisque cinq est positif, vous devrez déplacer cinq unités vers la droite. Si c'était négatif, vous vous déplaceriez de plus de 5 unités vers la gauche.
2 Déplacez-vous sur x unités à droite ou à gauche. Disons que vous travaillez avec le jeu de coordonnées (5, -4). Votre coordonnée x est 5. Puisque cinq est positif, vous devrez déplacer cinq unités vers la droite. Si c'était négatif, vous vous déplaceriez de plus de 5 unités vers la gauche.  3 Déplacez-vous sur y unités vers le haut ou le bas. Commencez là où vous l'avez laissé, 5 unités à droite de (0, 0). Puisque votre coordonnée y est de -4, vous devrez descendre de quatre unités. Si c'était 4, vous monteriez de quatre unités.
3 Déplacez-vous sur y unités vers le haut ou le bas. Commencez là où vous l'avez laissé, 5 unités à droite de (0, 0). Puisque votre coordonnée y est de -4, vous devrez descendre de quatre unités. Si c'était 4, vous monteriez de quatre unités.  4 Marquez le point. Marquez le point que vous avez trouvé en vous déplaçant de 5 unités vers la droite et de 4 unités vers le bas, le point (5, -4), situé dans le 4ème quadrant. Vous avez tous terminé.
4 Marquez le point. Marquez le point que vous avez trouvé en vous déplaçant de 5 unités vers la droite et de 4 unités vers le bas, le point (5, -4), situé dans le 4ème quadrant. Vous avez tous terminé.  1 Apprenez à représenter graphiquement des points si vous travaillez avec une équation. Si vous avez une formule sans aucune coordonnée, vous devrez alors trouver vos points en choisissant une coordonnée aléatoire pour x et en voyant ce que la formule crache pour y. Continuez jusqu'à ce que vous ayez trouvé suffisamment de points et que vous puissiez tous les tracer, en les connectant si nécessaire. Voici comment vous pouvez le faire, que vous travailliez avec une simple ligne ou avec une équation plus compliquée telle qu'une parabole:
1 Apprenez à représenter graphiquement des points si vous travaillez avec une équation. Si vous avez une formule sans aucune coordonnée, vous devrez alors trouver vos points en choisissant une coordonnée aléatoire pour x et en voyant ce que la formule crache pour y. Continuez jusqu'à ce que vous ayez trouvé suffisamment de points et que vous puissiez tous les tracer, en les connectant si nécessaire. Voici comment vous pouvez le faire, que vous travailliez avec une simple ligne ou avec une équation plus compliquée telle qu'une parabole:  2 Connectez les points si nécessaire. Si vous devez créer un graphique linéaire, dessiner un cercle ou relier tous les points d'une parabole ou d'une autre équation quadratique, vous devrez connecter les points. Si vous avez une équation linéaire, dessinez des lignes reliant les points de gauche à droite. Si vous travaillez avec une équation quadratique, connectez les points avec des lignes courbes.
2 Connectez les points si nécessaire. Si vous devez créer un graphique linéaire, dessiner un cercle ou relier tous les points d'une parabole ou d'une autre équation quadratique, vous devrez connecter les points. Si vous avez une équation linéaire, dessinez des lignes reliant les points de gauche à droite. Si vous travaillez avec une équation quadratique, connectez les points avec des lignes courbes.  3 Comprendre comment la modification de l’équation modifie le graphique. Voici les différentes manières dont la modification de l’équation modifie le graphique:
3 Comprendre comment la modification de l’équation modifie le graphique. Voici les différentes manières dont la modification de l’équation modifie le graphique:  4 Suivez un exemple pour voir comment modifier l'équation modifie le graphique. Considérons l’équation y = x ^ 2; une parabole avec sa base à (0,0). Voici les différences que vous verrez en modifiant l'équation:
4 Suivez un exemple pour voir comment modifier l'équation modifie le graphique. Considérons l’équation y = x ^ 2; une parabole avec sa base à (0,0). Voici les différences que vous verrez en modifiant l'équation: