Comment la constante mathématique appelée "pi" a-t-elle été découverte - et auriez-vous pu le découvrir? Eh bien, oui, avec un peu de travail, vous pouvez découvrir l'idée intelligente et la source du concept, ainsi que sa signification plus abstraite et trouver une valeur approximative. Il est enveloppé dans chaque cercle et chaque sphère, mais où et comment l'aviez-vous envisagé sous la forme de cercles? Continuez à lire pour des instructions détaillées pour votre saut dans les découvertes en mathématiques.

Méthode One of Four:
Géométrie de base du cercle dans un plan

  1. 1 Commencez à rafraîchir votre compréhension de la géométrie du cercle dans un plan. Vous en savez beaucoup sur le point, le plan et l'espace, et ils ne sont même pas définis dans l'étude de la géométrie, mais ils sont décrits tels qu'ils sont utilisés.
    • Qu'est-ce qu'un cercle? Les informations suivantes doivent faire partie de votre compréhension (élémentaire) des cercles, mais vous pouvez en apprendre beaucoup plus au fur et à mesure.
    • équidistant - est l'abréviation de "d'égale distance"
    • cercle - tous les points équidistants, du centre (point central).
    • Les faits suivants concernent mais sont ne pas partie du cercle:
      • centre - le point équidistant de tout point du cercle,
      • rayon - le segment (nomme la longueur) entre une extrémité au centre et l'autre extrémité sur le cercle (c'est cette "distance égale" mentionnée),
      • diamètre - le segment (nomme la longueur) par le centre et entre ses deux extrémités sur le cercle,
      • segment, secteur, secteur, et inclus ou inscrit formes à l'intérieur, mais ne pas partie de, le cercle et
      • circonférence - la distance une fois autour du cercle.
        • Oui, ce mot est long et étrange; alors, pensez à "la distance autour clôture circulaire."

Méthode deux sur quatre:
Créez d'abord une formule

  1. 1 Découvrez votre formule de circonférence: Le diamètre peut être courbé et placé bout à bout autour du cercle, soit environ trois fois - ce qui signifie que: Trois réiamètres plus une petite fraction de diamètre = Circumference. Appelons cela C = 3 X d, approximativement. Fait (c'était trop facile…), tout comme vous auriez dû le faire en découvrant la circonférence il y a environ 3000 ou 4000 ans; maintenant vous allez nettoyer cette idée… Dans les temps anciens, les mathématiques étaient comme une étude mystique et votre «découverte» faisait partie de l'expression des mystères mathématiques.
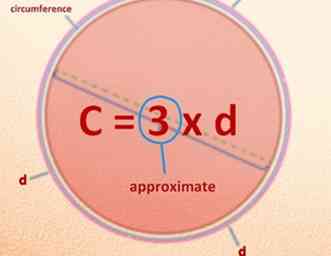  2. 2 Absorbez cette idée rugueuse et intuitive de pi, environ 3, et réalisez qu'il est facile de démontrer que ce n'est pas exactement trois. Maintenant, vous allez le rendre plus précis.

Méthode trois sur quatre:
Découvrez pi plus exactement

  1. 1 Numérotez quatre tailles différentes de conteneurs circulaires ou de couvercles. Un globe ou une boule (sphère) peut également fonctionner, mais il est plus difficile à mesurer.
  2. 2 Procurez-vous une ficelle non extensible et non crépue et un mètre, un mètre ou une règle.
  3. 3 Faire un graphique (ou un tableau) comme le suivant: Circonférence | diamètre | quotient C / d =?
    1. __________|________|__________________
    2. __________|________|__________________
    3. __________|________|__________________
    4. __________|________|__________________
  4. 4 Mesurez avec précision autour de chacun des quatre éléments circulaires en enroulant une chaîne parfaitement autour de lui. Marquez la distance une fois autour de la chaîne. C'est la circonférence: c'est comme un périmètre, mais, le périmètre d'un cercle--la distance autour d'un cercle - s'appelle la circonférence, ne pas périmètre, d'habitude.
  5. 5 Redressez et mesurez la partie de la chaîne que vous avez marquée comme la distance autour du cercle. Notez vos mesures de la circonférence en utilisant des décimales. Épingler ou scotcher les extrémités de la ficelle pour la mesurer avec précision (droite et étendue à sa pleine mesure), puisque vous auriez eu besoin de resserrer la ficelle autour de l’objet circulaire, alors maintenant vous la serrez dans le sens de la longueur.
  6. 6 Retournez le contenant afin de trouver et de marquer le centre en bas de manière à pouvoir mesurer le diamètre à l’aide de décimales (également appelées fractions décimales).
  7. 7 Mesurez à travers chaque cercle exactement au centre de chacun des quatre éléments avec une mesure de bord droit (mètre, mètre ou règle). C'est le diamètre.
    • Remarque: La multiplication de deux fois le rayon, c’est-à-dire: "2 X rayon = diamètre" est également écrite comme "2r = d".
  8. 8 Diviser chaque circonférence par le même diamètre de cercle. Les quatre problèmes de division de C / d = _____ devraient être d'environ 3 ou 3,1 (ou environ 3,14 si vos mesures sont exactes); alors qu'est-ce que pi: c'est un nombre. C'est un ratio. Il relie le diamètre à la circonférence. Bien sûr, utiliser des mesures précises à l’aide de diviseurs similaires à une boussole peut aider.
  9. 9 Faites la moyenne des quatre réponses au problème de la division en ajoutant ces quatre quotients et en divisant par 4, ce qui devrait donner un résultat plus précis (par exemple, si vos quatre divisions vous ont donné: 3.1 + 3.15 + 3.1 + 3.2 = ____ / 4 = ____? C'est 12.55 / 4 = 3.1375, et peut être arrondi à 3.14).
    C'est l'idée de "pi". Le nombre de diamètres qui fait la circonférence (tout le temps, donc c'est constant)… C'est la constante "pi". Ce nombre de diamètres.
    • De plus, le rayon correspondra à un peu plus de 6 fois (2 fois pi) autour d'un cercle, tout en sachant que le diamètre va trois fois; donc, cela implique une formule de circonférence C = 2 X 3,14 X r, ce qui est juste = 3,14 X d… en utilisant 2r est d ("Bien compris", acquiesce oui. "Oui!" il pénètre vraiment, si ce n'est pas encore clair).
  10. 10 Enfin, prenez la ficelle de diamètre et utilisez-la pour couper sa longueur sur la circonférence trois fois. Faites cela pour chacun des conteneurs. Le bout de ficelle restant de chacune des ficelles de circonférence aura environ la même longueur.La longueur de mesure de ce petit bout de ficelle doit être de 0,1415, ce qui est juste un exemple d’environ 3,14…

Méthode quatre sur quatre:
Astuce de l'enseignant

  1. 1 Aidez les élèves à vraiment apprécier cet exercice. Cela pourrait être un moment très agréable, un de ces moments où ils ont l'impression: "Je comprends! Wow!", "J'aime les maths plus que jamais / plus que je ne le pensais". Traitez cela comme une expérience scientifique, comme une sorte de travail interdisciplinaire «mathématiques / sciences».
  2. 2 Préparez une fiche de mission mystérieuse pour une classe ou un projet extérieur, si vous êtes enseignant ou tuteur.
  3. 3 Un peu "Montrez-les ou laissez-les vous montrer, mais faites ne pas Dis leur! Laissez-les découvrir des choses. "Si c'est un cadeau, alors le résultat est trop facile pour ce que tout cela montre. Alors, faites en sorte que les étudiants puissent le découvrir comme un mystère et avoir une" Eureka! expérience… ", ne pas juste entendre ou lire à propos d'une expérience.
    • Vous ne voudriez pas passer directement par une lecture ou une présentation de conférence comme ici, mais soyez subtil au premier chef, facilitez-le, puis clarifiez-le après avoir demandé aux élèves de présenter leurs tableaux comme des affiches de ce qu'ils ont découvert! Les étudiants peuvent afficher leurs présentations sur un mur de mathématiques et être fiers de leur intelligence, de leur ingéniosité et de leur expérience!
  4. 4 Utilisez-le comme un excellent projet de classe (enseignement transversal) "art-math-art" - ou pour que vos étudiants ramènent à la maison en tant que projet pour un crédit supplémentaire en dehors des cours de mathématiques. Et, après avoir appliqué celui-ci, vous voudrez peut-être explorer pour devenir un excellent professeur.