Comment trouver des points d'inflexion

En calcul, un point d'inflexion est un point sur une courbe où la courbure change de signe. Il est utilisé dans diverses disciplines, notamment l'ingénierie, l'économie et les statistiques, pour déterminer les changements fondamentaux dans les données. Si vous avez besoin de trouver les points d'inflexion d'une courbe, faites défiler jusqu'à la partie 2.

Première partie de trois:
Comprendre les points d'inflexion

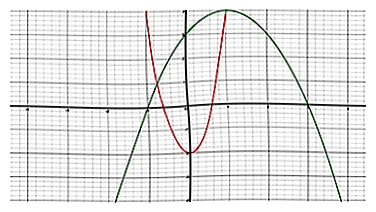
1. 1 Comprendre les fonctions concaves et concaves. Pour comprendre les points d'inflexion, vous devez faire la distinction entre les deux.
   • Une fonction concave vers le bas est une fonction où aucun segment de ligne qui relie deux points sur son graphique ne dépasse le graphique. Intuitivement, le graphique a la forme d'une colline.
   • Une fonction concave vers le haut, par contre, est une fonction où aucun segment de ligne qui relie deux points sur son graphique ne descend jamais en dessous du graphique. Il a la forme d'un U.
   • Dans le graphique ci-dessus, la courbe rouge est concave vers le haut, tandis que la courbe verte est concave vers le bas.
   • Les fonctions en général ont à la fois des intervalles concaves vers le haut et concaves. Les points d'inflexion existent lorsqu'une fonction change de concavité.
2. 2 Revoir les racines d'une fonction. Une racine d'une fonction est le point où la fonction est égale à zéro. Dans le graphique ci-dessus, nous pouvons voir que les racines de la parabole verte sont à $\ displaystyle x = -1$ et $\ displaystyle x = 3.$ Ce sont les points auxquels la fonction coupe l'axe des abscisses.

Deuxième partie de trois:
Trouver les dérivés d'une fonction

1. 1 Différencier. Avant de trouver un point d'inflexion, vous devrez trouver des dérivées de votre fonction. Les dérivés des fonctions de base peuvent être trouvés dans n'importe quel texte de calcul; vous devrez les apprendre avant de pouvoir passer à des tâches plus complexes. Les premières dérivés sont notées $\ displaystyle f ^ \ prime (x)$ ou $\ displaystyle \ frac \ mathrm d f \ mathrm d x.$
   • Dites que vous devez trouver le point d'inflexion de la fonction ci-dessous.
     • $\ displaystyle f (x) = x ^ 3 + 2x-1$
   • Utilisez la règle de puissance.
     • $\ displaystyle \ begin aligné f ^ \ prime (x) & = 3x ^ 3-1 + 2x ^ 1-1 \ & = 3x ^ 2 +2 \ end aligné$
2. 2 Différencier à nouveau. La seconde dérivée est la dérivée du dérivé et est notée $\ displaystyle f ^ \ prime \ prime (x)$ ou $\ displaystyle \ frac \ mathrm d ^ 2 f \ mathrm d x ^ 2.$
   • $\ displaystyle \ begin aligné f ^ \ prime \ prime (x) & = (2) (3) x ^ 2-1 \ & = 6x \ end aligné$
3. 3 Définissez la dérivée seconde égale à zéro et résolvez l'équation résultante. Votre réponse sera un possible point d'inflexion.
   • $\ displaystyle \ begin aligné 6x & = 0 \ x & = 0 \ end aligné$

Troisième partie de trois:
Trouver un point d'inflexion

1. 1 Vérifiez si la dérivée seconde change de signe au point candidat. Si le signe de la dérivée seconde change lorsque vous passez par le point d'inflexion candidat, il existe alors un point d'inflexion. Si le signe ne change pas, il n'y a pas de point d'inflexion.
   • Rappelez-vous que vous recherchez des changements de signe, sans évaluer la valeur. Dans les expressions plus compliquées, la substitution peut être indésirable, mais une attention particulière aux signes est souvent la solution beaucoup plus rapide. Par exemple, au lieu d’évaluer les chiffres immédiatement, nous pourrions plutôt examiner certains termes et les juger positifs ou négatifs.
   • Dans notre exemple, $\ displaystyle f ^ \ prime \ prime (x) = 6x.$ Puis brancher un négatif $\ displaystyle x$ donne un négatif $\ displaystyle f ^ \ prime \ prime (x),$ tout en branchant un positif $\ displaystyle x$ donne un résultat positif $\ displaystyle f ^ \ prime \ prime (x).$ Donc, $\ displaystyle x = 0$ est un point d'inflexion de la fonction $\ displaystyle f (x) = x ^ 3 + 2x-1.$ Il n'était pas nécessaire d'évaluer réellement pour nos valeurs choisies.
2. 2 Remplacez à nouveau la fonction d'origine.
   • $\ displaystyle f (0) = (0) ^ 3 +2 (0) -1 = -1.$
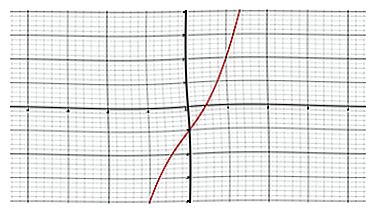3. 3 Trouvez le point d'inflexion. La coordonnée du point d'inflexion est notée $\ displaystyle (x, f (x)).$ Dans ce cas, $\ displaystyle (0, -1),$ comme indiqué ci-dessus.