Apprendre l'algèbre peut sembler intimidant, mais une fois que vous avez compris, ce n'est pas si difficile! Il vous suffit de suivre l'ordre pour compléter certaines parties de l'équation et de garder votre travail organisé pour éviter les erreurs!
Première partie de cinq:
Apprendre les règles de base en algèbre
-
 1 Examinez vos opérations mathématiques de base. Pour commencer à apprendre l'algèbre, vous devez connaître les compétences de base en mathématiques, telles que l'ajout, la soustraction, la multiplication et la division. Cette mathématique primaire / élémentaire est essentielle avant de commencer à apprendre l'algèbre. Si vous ne maîtrisez pas ces compétences, il sera difficile d’aborder les concepts plus complexes enseignés en algèbre. Si vous avez besoin d'un rappel sur ces opérations, essayez notre article sur les compétences de base en mathématiques.
1 Examinez vos opérations mathématiques de base. Pour commencer à apprendre l'algèbre, vous devez connaître les compétences de base en mathématiques, telles que l'ajout, la soustraction, la multiplication et la division. Cette mathématique primaire / élémentaire est essentielle avant de commencer à apprendre l'algèbre. Si vous ne maîtrisez pas ces compétences, il sera difficile d’aborder les concepts plus complexes enseignés en algèbre. Si vous avez besoin d'un rappel sur ces opérations, essayez notre article sur les compétences de base en mathématiques. - Vous n'avez pas nécessairement besoin d'être génial à faire ces opérations de base dans votre tête pour faire des problèmes d'algèbre. De nombreuses classes d'algèbre vous permettront d'utiliser une calculatrice pour gagner du temps lors de ces opérations simples. Cependant, vous devez au moins savoir comment effectuer ces opérations sans calculatrice lorsque vous n'êtes pas autorisé à en utiliser une.
-
 2 Connaître l'ordre des opérations. L'une des choses les plus délicates dans la résolution d'une équation d'algèbre en tant que débutant est de savoir par où commencer. Heureusement, il existe un ordre spécifique pour résoudre ces problèmes: faites d'abord des opérations mathématiques entre parenthèses, puis faites des exposants, puis multipliez, divisez, puis ajoutez et enfin soustrayez. Un outil pratique pour se souvenir de cet ordre d'opérations est l'acronyme PEMDAS. Découvrez comment appliquer l'ordre des opérations ici. Pour rappel, l'ordre des opérations est le suivant:
2 Connaître l'ordre des opérations. L'une des choses les plus délicates dans la résolution d'une équation d'algèbre en tant que débutant est de savoir par où commencer. Heureusement, il existe un ordre spécifique pour résoudre ces problèmes: faites d'abord des opérations mathématiques entre parenthèses, puis faites des exposants, puis multipliez, divisez, puis ajoutez et enfin soustrayez. Un outil pratique pour se souvenir de cet ordre d'opérations est l'acronyme PEMDAS. Découvrez comment appliquer l'ordre des opérations ici. Pour rappel, l'ordre des opérations est le suivant: - Parentheses
- Exponents
- Multiplication
- réivision
- UNEddition
- Sextraction
- L'ordre des opérations est important en algèbre car faire les opérations dans un problème d'algèbre dans le mauvais ordre peut parfois affecter la réponse. Par exemple, si nous traitons du problème de mathématiques 8 + 2 × 5, si nous ajoutons 2 à 8 en premier, nous obtenons 10 × 5 = 50, mais si on multiplie 2 et 5 en premier, on obtient 8 + 10 = 18. Seule la deuxième réponse est correcte.
-
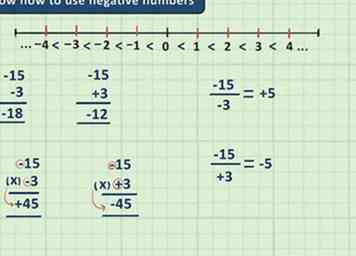 3 Savoir utiliser des nombres négatifs. En algèbre, il est courant d'utiliser des nombres négatifs, il est donc judicieux d'examiner comment ajouter, soustraire, multiplier et diviser les négatifs avant de commencer à apprendre l'algèbre. Vous trouverez ci-dessous quelques notions de base concernant les nombres négatifs. Pour plus d'informations, consultez nos articles sur l'ajout et la soustraction de nombres négatifs et la division et la multiplication des nombres négatifs.
3 Savoir utiliser des nombres négatifs. En algèbre, il est courant d'utiliser des nombres négatifs, il est donc judicieux d'examiner comment ajouter, soustraire, multiplier et diviser les négatifs avant de commencer à apprendre l'algèbre. Vous trouverez ci-dessous quelques notions de base concernant les nombres négatifs. Pour plus d'informations, consultez nos articles sur l'ajout et la soustraction de nombres négatifs et la division et la multiplication des nombres négatifs. - Sur une droite numérique, une version négative d'un nombre est à la même distance de zéro que le positif, mais dans la direction opposée.
- Ajouter deux nombres négatifs ensemble fait le nombre plus négatif (en d’autres termes, les chiffres seront plus élevés, mais comme le nombre est négatif, il est considéré comme inférieur)
- Deux signes négatifs s'annulent - soustraire un nombre négatif revient à ajouter un nombre positif
- Multiplier ou diviser deux nombres négatifs donne une réponse positive.
- Multiplier ou diviser un nombre positif et un nombre négatif donne une réponse négative.
-
 4 Savoir organiser de longs problèmes. Bien que les problèmes simples d'algèbre puissent être résolus, des problèmes plus complexes peuvent nécessiter de nombreuses étapes. Pour éviter les erreurs, organisez votre travail en commençant une nouvelle ligne chaque fois que vous franchissez une étape vers la résolution de votre problème. Si vous avez affaire à une équation à deux côtés, essayez d'écrire tous les signes égaux ("=" s) les uns en dessous des autres. De cette façon, si vous faites une erreur quelque part, ce sera beaucoup plus facile à trouver et à corriger.
4 Savoir organiser de longs problèmes. Bien que les problèmes simples d'algèbre puissent être résolus, des problèmes plus complexes peuvent nécessiter de nombreuses étapes. Pour éviter les erreurs, organisez votre travail en commençant une nouvelle ligne chaque fois que vous franchissez une étape vers la résolution de votre problème. Si vous avez affaire à une équation à deux côtés, essayez d'écrire tous les signes égaux ("=" s) les uns en dessous des autres. De cette façon, si vous faites une erreur quelque part, ce sera beaucoup plus facile à trouver et à corriger. - Par exemple, pour résoudre l'équation 9/3 - 5 + 3 × 4, nous pourrions garder notre problème organisé comme suit:
-
- 9/3 - 5 + 3 × 4
- 9/3 - 5 + 12
- 3 - 5 + 12
- 3 + 7
- 10
-
- Par exemple, pour résoudre l'équation 9/3 - 5 + 3 × 4, nous pourrions garder notre problème organisé comme suit:
Deuxième partie de cinq:
Comprendre les variables
-
 1 Recherchez les symboles qui ne sont pas des nombres. En algèbre, vous commencerez à voir des lettres et des symboles apparaître dans vos problèmes mathématiques, plutôt que de simples chiffres. Ce sont des variables. Les variables ne sont pas aussi déroutantes qu’elles peuvent paraître au premier abord - ce ne sont que des moyens de montrer des nombres avec des valeurs inconnues. Vous trouverez ci-dessous quelques exemples courants de variables en algèbre:
1 Recherchez les symboles qui ne sont pas des nombres. En algèbre, vous commencerez à voir des lettres et des symboles apparaître dans vos problèmes mathématiques, plutôt que de simples chiffres. Ce sont des variables. Les variables ne sont pas aussi déroutantes qu’elles peuvent paraître au premier abord - ce ne sont que des moyens de montrer des nombres avec des valeurs inconnues. Vous trouverez ci-dessous quelques exemples courants de variables en algèbre: - Des lettres comme x, y, z, a, b et c
- Lettres grecques comme thêta ou θ
- Notez que pas tout les symboles sont des variables inconnues. Par exemple, pi, ou π, est toujours égal à environ 3,14159.
-
 2 Pensez aux variables comme des nombres "inconnus". Comme mentionné ci-dessus, les variables sont essentiellement des nombres avec des valeurs inconnues. En d'autres termes, il y a un certain nombre cela peut aller à la place de la variable pour faire fonctionner l'équation. Généralement, votre objectif dans un problème d'algèbre est de déterminer quelle est la variable - considérez-la comme un "numéro mystère" que vous essayez de découvrir.
2 Pensez aux variables comme des nombres "inconnus". Comme mentionné ci-dessus, les variables sont essentiellement des nombres avec des valeurs inconnues. En d'autres termes, il y a un certain nombre cela peut aller à la place de la variable pour faire fonctionner l'équation. Généralement, votre objectif dans un problème d'algèbre est de déterminer quelle est la variable - considérez-la comme un "numéro mystère" que vous essayez de découvrir. - Par exemple, dans l'équation 2x + 3 = 11, x est notre variable. Cela signifie qu'il y a une valeur qui va à la place de x pour que le côté gauche de l'équation soit égal à 11. Puisque 2 × 4 + 3 = 11, dans ce cas, x = 4.
- Un moyen facile de comprendre les variables consiste à les remplacer par des points d'interrogation dans les problèmes d'algèbre. Par exemple, nous pourrions réécrire l'équation 2 + 3 + x = 9 comme 2 + 3 + ? = 9. Cela facilite la compréhension de ce que nous essayons de faire - nous avons juste besoin de savoir quel nombre ajouter à 2 + 3 = 5 pour obtenir 9. La réponse est encore une fois 4, bien sûr.
-
 3 Surveillez les variables récurrentes. Si une variable apparaît plus d'une fois, simplifiez les variables. Que faites-vous si la même variable apparaît plus d'une fois dans l'équation? Bien que cette situation puisse sembler délicate à résoudre, vous pouvez réellement traiter les variables comme vous traitez les nombres normaux - en d'autres termes, vous pouvez les ajouter, les soustraire, etc., tant que vous ne combinez que des variables identiques. En d'autres termes, x + x = 2x, mais x + y n'est pas égal à 2xy.
3 Surveillez les variables récurrentes. Si une variable apparaît plus d'une fois, simplifiez les variables. Que faites-vous si la même variable apparaît plus d'une fois dans l'équation? Bien que cette situation puisse sembler délicate à résoudre, vous pouvez réellement traiter les variables comme vous traitez les nombres normaux - en d'autres termes, vous pouvez les ajouter, les soustraire, etc., tant que vous ne combinez que des variables identiques. En d'autres termes, x + x = 2x, mais x + y n'est pas égal à 2xy. - Par exemple, regardons l'équation 2x + 1x = 9. Dans ce cas, nous pouvons ajouter 2x et 1x ensemble pour obtenir 3x = 9. Puisque 3 x 3 = 9, nous savons que x = 3.
- Notez à nouveau que vous ne pouvez ajouter que les mêmes variables. Dans l'équation 2x + 1y = 9, nous ne pouvons pas combiner 2x et 1y car ce sont deux variables différentes.
- Cela est également vrai quand une variable a un exposant différent d'un autre. Par exemple, dans l'équation 2x + 3x2 = 10, on ne peut pas combiner 2x et 3x2 car les variables x ont des exposants différents. Voir Comment ajouter des exposants pour plus d'informations.
Troisième partie de cinq:
Apprendre à résoudre des équations en "annulant"
-
 1 Essayez d'obtenir la variable par elle-même dans les équations algébriques. Résoudre une équation en algèbre signifie généralement découvrir quelle est la variable. Les équations algébriques sont généralement configurées avec des nombres et / ou des variables des deux côtés, comme ceci: x + 2 = 9 × 4. Pour déterminer quelle est la variable, vous devez l'obtenir seule d'un côté du signe égal. Tout ce qui reste de l'autre côté du signe égal est votre réponse.
1 Essayez d'obtenir la variable par elle-même dans les équations algébriques. Résoudre une équation en algèbre signifie généralement découvrir quelle est la variable. Les équations algébriques sont généralement configurées avec des nombres et / ou des variables des deux côtés, comme ceci: x + 2 = 9 × 4. Pour déterminer quelle est la variable, vous devez l'obtenir seule d'un côté du signe égal. Tout ce qui reste de l'autre côté du signe égal est votre réponse. - Dans l'exemple (x + 2 = 9 × 4), pour obtenir x par lui-même sur le côté gauche de l'équation, il faut se débarrasser du "+ 2". Pour ce faire, nous allons simplement soustraire 2 de ce côté, en nous laissant x = 9 × 4. Cependant, pour garder les deux côtés de l'équation égaux, nous devons également soustraire 2 de l'autre côté. Cela nous laisse avec x = 9 × 4 - 2. Suivant l'ordre des opérations, nous multiplions d'abord, puis soustrayons, nous donnant une réponse de x = 36 - 2 = 34.
-
 2 Annuler l'addition avec soustraction (et vice versa). Comme nous venons de le voir ci-dessus, obtenir x par lui-même d'un côté du signe égal signifie généralement se débarrasser des nombres à côté. Pour ce faire, nous effectuons l'opération "opposée" des deux côtés de l'équation. Par exemple, dans l'équation x + 3 = 0, puisque nous voyons un "+ 3" à côté de notre x, nous placerons un "- 3" des deux côtés. Le "+ 3" et "- 3", laissant x par lui-même et "-3" de l'autre côté du signe égal, comme ceci: x = -3.
2 Annuler l'addition avec soustraction (et vice versa). Comme nous venons de le voir ci-dessus, obtenir x par lui-même d'un côté du signe égal signifie généralement se débarrasser des nombres à côté. Pour ce faire, nous effectuons l'opération "opposée" des deux côtés de l'équation. Par exemple, dans l'équation x + 3 = 0, puisque nous voyons un "+ 3" à côté de notre x, nous placerons un "- 3" des deux côtés. Le "+ 3" et "- 3", laissant x par lui-même et "-3" de l'autre côté du signe égal, comme ceci: x = -3. - En général, l'addition et la soustraction sont comme des "opposés" - faites-en un pour vous débarrasser de l'autre. Voir ci-dessous:
-
- Pour plus, soustrayez. Exemple: x + 9 = 3 → x = 3 - 9
- Pour la soustraction, ajoutez. Exemple: x - 4 = 20 → x = 20 + 4
-
- En général, l'addition et la soustraction sont comme des "opposés" - faites-en un pour vous débarrasser de l'autre. Voir ci-dessous:
-
 3 Annuler la multiplication avec division (et vice versa). La multiplication et la division sont un peu plus difficiles à travailler que l'addition et la soustraction, mais elles ont la même relation "opposée". Si vous voyez un "× 3" sur un côté, vous l’annulerez en divisant les deux côtés par 3, et ainsi de suite.
3 Annuler la multiplication avec division (et vice versa). La multiplication et la division sont un peu plus difficiles à travailler que l'addition et la soustraction, mais elles ont la même relation "opposée". Si vous voyez un "× 3" sur un côté, vous l’annulerez en divisant les deux côtés par 3, et ainsi de suite. - Avec la multiplication et la division, vous devez effectuer l'opération inverse sur tout de l'autre côté du signe égal, même si c'est plus d'un numéro. Voir ci-dessous:
-
- Pour la multiplication, divisez. Exemple: 6x = 14 + 2 → x = (14 + 2)/6
- Pour la division, multipliez. Exemple: x / 5 = 25 → x = 25 × 5
-
- Avec la multiplication et la division, vous devez effectuer l'opération inverse sur tout de l'autre côté du signe égal, même si c'est plus d'un numéro. Voir ci-dessous:
-
 4 Annulez les exposants en prenant la racine (et vice versa). Les exposants sont un sujet de pré-algèbre assez avancé - si vous ne savez pas comment les faire, consultez notre article exposant de base pour plus d'informations. Le "contraire" d'un exposant est la racine qui a le même nombre que lui. Par exemple, le contraire du 2 l'exposant est une racine carrée (√), l'opposé du 3 exposant est la racine du cube (3√), et ainsi de suite.
4 Annulez les exposants en prenant la racine (et vice versa). Les exposants sont un sujet de pré-algèbre assez avancé - si vous ne savez pas comment les faire, consultez notre article exposant de base pour plus d'informations. Le "contraire" d'un exposant est la racine qui a le même nombre que lui. Par exemple, le contraire du 2 l'exposant est une racine carrée (√), l'opposé du 3 exposant est la racine du cube (3√), et ainsi de suite. - Cela peut être un peu déroutant, mais dans ces cas-là, vous prenez la racine des deux côtés lorsque vous traitez un exposant. D'autre part, vous prenez l'exposant des deux côtés quand vous avez affaire à une racine. Voir ci-dessous:
-
- Pour les exposants, prenez la racine. Exemple: x2 = 49 → x = √49
- Pour les racines, prenez l'exposant. Exemple: √x = 12 → x = 122
-
- Cela peut être un peu déroutant, mais dans ces cas-là, vous prenez la racine des deux côtés lorsque vous traitez un exposant. D'autre part, vous prenez l'exposant des deux côtés quand vous avez affaire à une racine. Voir ci-dessous:
Partie quatre de cinq:
Aiguiser vos compétences en algèbre
-
 1 Utilisez des images pour clarifier les problèmes. Si vous éprouvez de la difficulté à visualiser un problème d'algèbre, essayez d'utiliser des diagrammes ou des images pour illustrer votre équation. Vous pouvez même essayer d'utiliser un groupe d'objets physiques (comme des blocs ou des pièces de monnaie) à la place si vous en avez à portée de main.
1 Utilisez des images pour clarifier les problèmes. Si vous éprouvez de la difficulté à visualiser un problème d'algèbre, essayez d'utiliser des diagrammes ou des images pour illustrer votre équation. Vous pouvez même essayer d'utiliser un groupe d'objets physiques (comme des blocs ou des pièces de monnaie) à la place si vous en avez à portée de main. - Par exemple, résolvons l'équation x + 2 = 3 en utilisant des cases (☐)
-
- x +2 = 3
- ☒+☐☐ =☐☐☐
- À ce stade, nous allons soustraire 2 des deux côtés en retirant simplement 2 cases (☐☐) des deux côtés:
- ☒+☐☐-☐☐ =☐☐☐-☐☐
- ☒ = ☐ ou x = 1
-
- Comme autre exemple, essayons 2x = 4
-
- ☒☒ =☐☐☐☐
- À ce stade, nous diviserons les deux côtés par deux en séparant les cases de chaque côté en deux groupes:
- ☒|☒ =☐☐|☐☐
- ☒ = ☐☐ ou x = 2
-
- Par exemple, résolvons l'équation x + 2 = 3 en utilisant des cases (☐)
-
 2 Utilisez des "tests de bon sens" (en particulier pour les problèmes de mots). Lorsque vous convertissez un problème de mot en algèbre, essayez de vérifier votre formule en connectant des valeurs simples à votre variable. Est-ce que votre équation a du sens quand x = 0? Quand x = 1? Quand x = -1? Il est facile de faire des erreurs simples en écrivant p = 6d quand vous parlez de p = d / 6, mais ces erreurs sont facilement détectées si vous faites une vérification rapide de votre travail avant d'aller plus loin.
2 Utilisez des "tests de bon sens" (en particulier pour les problèmes de mots). Lorsque vous convertissez un problème de mot en algèbre, essayez de vérifier votre formule en connectant des valeurs simples à votre variable. Est-ce que votre équation a du sens quand x = 0? Quand x = 1? Quand x = -1? Il est facile de faire des erreurs simples en écrivant p = 6d quand vous parlez de p = d / 6, mais ces erreurs sont facilement détectées si vous faites une vérification rapide de votre travail avant d'aller plus loin. - Par exemple, supposons que l'on nous dise qu'un terrain de football mesure 30 verges (27,4 m) de plus que la largeur. Nous utilisons l'équation l = w + 30 pour représenter cela. Nous pouvons tester si cette équation a du sens en branchant des valeurs simples pour w. Par exemple, si le terrain a une largeur de 10 verges (9,1 m), il aura 10 + 30 = 40 verges (36 m) de long. Si sa largeur est de 30 verges (27,4 m), ce sera 30 + 30 = 60 verges (54,9 m) de long, et ainsi de suite. Cela a du sens - nous nous attendons à ce que le champ s'allonge à mesure qu'il s'élargit, donc cette équation est raisonnable.
-
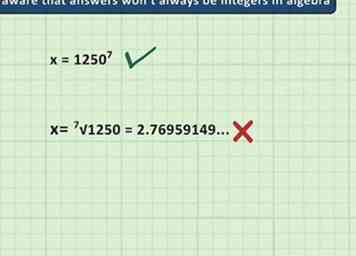 3 Sachez que les réponses ne seront pas toujours des nombres entiers en algèbre. Les réponses en algèbre et les autres formes avancées de mathématiques ne sont pas toujours des nombres simples et ronds. Ils peuvent souvent être des nombres décimaux, des fractions ou des nombres irrationnels. Une calculatrice peut vous aider à trouver ces réponses compliquées, mais gardez à l'esprit que votre professeur peut vous demander de donner votre réponse sous sa forme exacte, et non avec une décimale lourde.
3 Sachez que les réponses ne seront pas toujours des nombres entiers en algèbre. Les réponses en algèbre et les autres formes avancées de mathématiques ne sont pas toujours des nombres simples et ronds. Ils peuvent souvent être des nombres décimaux, des fractions ou des nombres irrationnels. Une calculatrice peut vous aider à trouver ces réponses compliquées, mais gardez à l'esprit que votre professeur peut vous demander de donner votre réponse sous sa forme exacte, et non avec une décimale lourde. - Par exemple, disons que nous réduisons une équation d'algèbre à x = 12507. Si on tape 12507 dans une calculatrice, nous obtiendrons une énorme chaîne de décimales (de plus, l'écran de la calculatrice étant trop grand, il ne peut pas afficher la réponse complète). Dans ce cas, nous pouvons représenter notre réponse simplement 12507 ou bien simplifier la réponse en l’écrivant en notation scientifique.
-
 4 Essayez d'étendre vos compétences. Lorsque vous êtes en confiance avec l'algèbre de base, essayez la factorisation. L'une des compétences les plus délicates en algèbre est la factorisation - une sorte de raccourci pour obtenir des équations complexes dans des formes simples. L'affacturage est un sujet d'algèbre semi-avancé, alors pensez à consulter l'article lié ci-dessus si vous avez des difficultés à le maîtriser. Vous trouverez ci-dessous quelques astuces pour la factorisation des équations:
4 Essayez d'étendre vos compétences. Lorsque vous êtes en confiance avec l'algèbre de base, essayez la factorisation. L'une des compétences les plus délicates en algèbre est la factorisation - une sorte de raccourci pour obtenir des équations complexes dans des formes simples. L'affacturage est un sujet d'algèbre semi-avancé, alors pensez à consulter l'article lié ci-dessus si vous avez des difficultés à le maîtriser. Vous trouverez ci-dessous quelques astuces pour la factorisation des équations: - Les équations avec la forme ax + ba facteur à a (x + b). Exemple: 2x + 4 = 2 (x + 2)
- Equations à la forme ax2 + bx facteur à cx ((a / c) x + (b / c)) où c est le plus grand nombre qui se divise en a et b de manière égale. Exemple: 3y2 + 12y = 3y (y + 4)
- Equations à la forme x2 + bx + facteur c à (x + y) (x + z) où y × z = c et yx + zx = bx. Exemple: x2 + 4x + 3 = (x + 3) (x + 1).
-
 5 Pratique, pratique, pratique! Les progrès en algèbre (et tout autre type de mathématiques) exigent beaucoup de travail et de répétition. Ne vous inquiétez pas - en faisant attention en classe, en effectuant toutes vos tâches et en cherchant de l'aide auprès de votre enseignant ou d'autres élèves quand vous en avez besoin, l'algèbre va commencer à devenir une seconde nature.
5 Pratique, pratique, pratique! Les progrès en algèbre (et tout autre type de mathématiques) exigent beaucoup de travail et de répétition. Ne vous inquiétez pas - en faisant attention en classe, en effectuant toutes vos tâches et en cherchant de l'aide auprès de votre enseignant ou d'autres élèves quand vous en avez besoin, l'algèbre va commencer à devenir une seconde nature. -
 6 Demandez à votre professeur de vous aider à comprendre les sujets délicats de l’algèbre. Si vous avez du mal à maîtriser l'algèbre, ne vous inquiétez pas, vous n'avez pas à l'apprendre par vous-même. Votre enseignant est la première personne à laquelle vous devez vous adresser avec des questions. Après le cours, demandez poliment à votre professeur de vous aider. Les bons enseignants seront généralement disposés à ré-expliquer le sujet de la journée lors d'un rendez-vous après l'école et peuvent même être en mesure de vous donner du matériel de pratique supplémentaire.
6 Demandez à votre professeur de vous aider à comprendre les sujets délicats de l’algèbre. Si vous avez du mal à maîtriser l'algèbre, ne vous inquiétez pas, vous n'avez pas à l'apprendre par vous-même. Votre enseignant est la première personne à laquelle vous devez vous adresser avec des questions. Après le cours, demandez poliment à votre professeur de vous aider. Les bons enseignants seront généralement disposés à ré-expliquer le sujet de la journée lors d'un rendez-vous après l'école et peuvent même être en mesure de vous donner du matériel de pratique supplémentaire. - Si, pour une raison quelconque, votre enseignant ne peut pas vous aider, demandez-lui de vous proposer des options de tutorat dans votre école. De nombreuses écoles auront une sorte de programme après l'école qui peut vous aider à obtenir le temps et l'attention supplémentaires dont vous avez besoin pour exceller dans votre algèbre. Rappelez-vous, utiliser une aide gratuite à votre disposition n'est pas quelque chose de gênant - c'est un signe que vous êtes assez intelligent pour résoudre votre problème!
Partie cinq de cinq:
Explorer des sujets intermédiaires
-
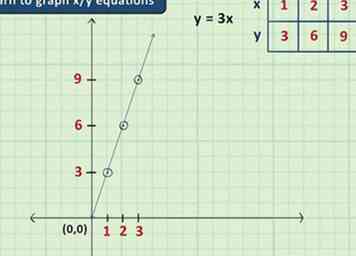 1 Apprenez à représenter graphiquement les équations x / y. Les graphes peuvent être des outils précieux en algèbre car ils vous permettent d'afficher des idées pour lesquelles vous avez généralement besoin de chiffres dans des images faciles à comprendre. En général, en algèbre, les problèmes graphiques se limitent à des équations à deux variables (généralement x et y) et se font sur un simple graphique à deux dimensions avec un axe x et un axe y. Avec ces équations, tout ce que vous avez à faire est de brancher une valeur pour x, puis de résoudre y (ou de faire l'inverse) pour obtenir deux nombres correspondant à un point du graphique.
1 Apprenez à représenter graphiquement les équations x / y. Les graphes peuvent être des outils précieux en algèbre car ils vous permettent d'afficher des idées pour lesquelles vous avez généralement besoin de chiffres dans des images faciles à comprendre. En général, en algèbre, les problèmes graphiques se limitent à des équations à deux variables (généralement x et y) et se font sur un simple graphique à deux dimensions avec un axe x et un axe y. Avec ces équations, tout ce que vous avez à faire est de brancher une valeur pour x, puis de résoudre y (ou de faire l'inverse) pour obtenir deux nombres correspondant à un point du graphique. - Par exemple, dans l'équation y = 3x, si on branche 2 pour x, on obtient y = 6. Cela signifie que le point (2,6) (deux espaces à droite du centre et six espaces au-dessus du centre) fait partie du graphique de cette équation.
- Les équations avec la forme y = mx + b (où m et b sont des nombres) sont notamment commun en algèbre de base. Ces équations ont toujours une pente de m et franchissent l'axe y à y = b.
-
 2 Apprenez à résoudre les inégalités. Que faites-vous quand votre équation n'utilise pas un signe égal? Rien de bien différent de ce que vous feriez normalement, il s'avère que Pour les inégalités, qui utilisent des signes comme> ("supérieur à") et <("inférieur à"), résolvez simplement comme d'habitude. Vous serez laissé avec une réponse qui est soit inférieure ou supérieure à votre variable.
2 Apprenez à résoudre les inégalités. Que faites-vous quand votre équation n'utilise pas un signe égal? Rien de bien différent de ce que vous feriez normalement, il s'avère que Pour les inégalités, qui utilisent des signes comme> ("supérieur à") et <("inférieur à"), résolvez simplement comme d'habitude. Vous serez laissé avec une réponse qui est soit inférieure ou supérieure à votre variable. - Par exemple, avec l'équation 3> 5x - 2, nous résoudrions comme nous le ferions pour une équation normale:
-
- 3> 5x - 2
- 5> 5x
- 1> x ou x <1.
-
- Cela signifie que chaque nombre moins d'un travaille pour x. En d'autres termes, x peut être 0, -1, -2, etc. Si nous connectons ces nombres dans l'équation de x, nous obtiendrons toujours une réponse inférieure à 3.
- Par exemple, avec l'équation 3> 5x - 2, nous résoudrions comme nous le ferions pour une équation normale:
-
 3 S'attaquer aux équations quadratiques. Un sujet d'algèbre avec lequel beaucoup de débutants luttent est la résolution d'équations quadratiques. Les quadratiques sont des équations avec la forme ax2 + bx + c = 0, où a, b et c sont des nombres (sauf que a ne peut pas être 0.) Ces équations sont résolues avec la formule x = [-b +/- √ (b2 - 4ac)] / 2a. Faites attention - le signe +/- signifie que vous devez trouver les réponses pour ajouter et soustraire, de sorte que vous pouvez avoir deux réponses à ces types de problèmes.
3 S'attaquer aux équations quadratiques. Un sujet d'algèbre avec lequel beaucoup de débutants luttent est la résolution d'équations quadratiques. Les quadratiques sont des équations avec la forme ax2 + bx + c = 0, où a, b et c sont des nombres (sauf que a ne peut pas être 0.) Ces équations sont résolues avec la formule x = [-b +/- √ (b2 - 4ac)] / 2a. Faites attention - le signe +/- signifie que vous devez trouver les réponses pour ajouter et soustraire, de sorte que vous pouvez avoir deux réponses à ces types de problèmes. - A titre d'exemple, résolvons la formule quadratique 3x2 + 2x -1 = 0.
-
- x = [-b +/- √ (b2 - 4ac)] / 2a
- x = [-2 +/- √ (22 - 4(3)(-1))]/2(3)
- x = [-2 +/- √ (4 - (-12))] / 6
- x = [-2 +/- √ (16)] / 6
- x = [-2 +/- 4] / 6
- x = -1 et 1/3
-
- A titre d'exemple, résolvons la formule quadratique 3x2 + 2x -1 = 0.
-
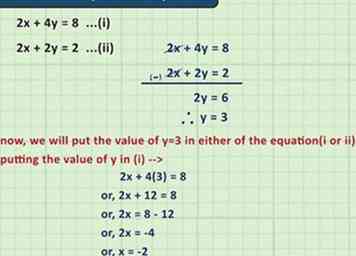 4 Expérimentez avec des systèmes d'équations. Résoudre plus d'une équation à la fois peut sembler super difficile, mais lorsque vous travaillez avec des équations d'algèbre simples, ce n'est pas si difficile. Les enseignants d'algèbre utilisent souvent une approche graphique pour résoudre ces problèmes. Lorsque vous travaillez avec un système de deux équations, les solutions sont les points sur un graphique auxquels les lignes des deux équations se croisent.
4 Expérimentez avec des systèmes d'équations. Résoudre plus d'une équation à la fois peut sembler super difficile, mais lorsque vous travaillez avec des équations d'algèbre simples, ce n'est pas si difficile. Les enseignants d'algèbre utilisent souvent une approche graphique pour résoudre ces problèmes. Lorsque vous travaillez avec un système de deux équations, les solutions sont les points sur un graphique auxquels les lignes des deux équations se croisent. - Par exemple, supposons que nous travaillons avec un système contenant les équations y = 3x - 2 et y = -x - 6. Si nous dessinons ces deux lignes sur un graphique, nous obtenons une ligne qui monte à un angle raide , et celui qui descend à un angle doux. Puisque ces lignes se croisent au point (-1,-5), c'est une solution pour le système.[1]
- Si nous voulons vérifier notre problème, nous pouvons le faire en branchant notre réponse dans les équations du système - une bonne réponse devrait "fonctionner" pour les deux.
-
- y = 3x - 2
- -5 = 3(-1) - 2
- -5 = -3 - 2
- -5 = -5
- y = -x - 6
- -5 = -(-1) - 6
- -5 = 1 - 6
- -5 = -5
-
- Les deux équations "check out", donc notre réponse est correcte!
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Examinez vos opérations mathématiques de base. Pour commencer à apprendre l'algèbre, vous devez connaître les compétences de base en mathématiques, telles que l'ajout, la soustraction, la multiplication et la division. Cette mathématique primaire / élémentaire est essentielle avant de commencer à apprendre l'algèbre. Si vous ne maîtrisez pas ces compétences, il sera difficile d’aborder les concepts plus complexes enseignés en algèbre. Si vous avez besoin d'un rappel sur ces opérations, essayez notre article sur les compétences de base en mathématiques.
1 Examinez vos opérations mathématiques de base. Pour commencer à apprendre l'algèbre, vous devez connaître les compétences de base en mathématiques, telles que l'ajout, la soustraction, la multiplication et la division. Cette mathématique primaire / élémentaire est essentielle avant de commencer à apprendre l'algèbre. Si vous ne maîtrisez pas ces compétences, il sera difficile d’aborder les concepts plus complexes enseignés en algèbre. Si vous avez besoin d'un rappel sur ces opérations, essayez notre article sur les compétences de base en mathématiques.  2 Connaître l'ordre des opérations. L'une des choses les plus délicates dans la résolution d'une équation d'algèbre en tant que débutant est de savoir par où commencer. Heureusement, il existe un ordre spécifique pour résoudre ces problèmes: faites d'abord des opérations mathématiques entre parenthèses, puis faites des exposants, puis multipliez, divisez, puis ajoutez et enfin soustrayez. Un outil pratique pour se souvenir de cet ordre d'opérations est l'acronyme PEMDAS. Découvrez comment appliquer l'ordre des opérations ici. Pour rappel, l'ordre des opérations est le suivant:
2 Connaître l'ordre des opérations. L'une des choses les plus délicates dans la résolution d'une équation d'algèbre en tant que débutant est de savoir par où commencer. Heureusement, il existe un ordre spécifique pour résoudre ces problèmes: faites d'abord des opérations mathématiques entre parenthèses, puis faites des exposants, puis multipliez, divisez, puis ajoutez et enfin soustrayez. Un outil pratique pour se souvenir de cet ordre d'opérations est l'acronyme PEMDAS. Découvrez comment appliquer l'ordre des opérations ici. Pour rappel, l'ordre des opérations est le suivant: 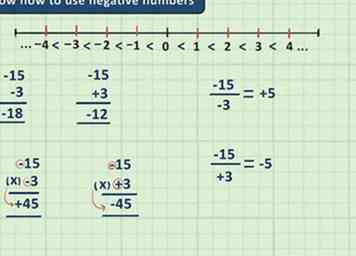 3 Savoir utiliser des nombres négatifs. En algèbre, il est courant d'utiliser des nombres négatifs, il est donc judicieux d'examiner comment ajouter, soustraire, multiplier et diviser les négatifs avant de commencer à apprendre l'algèbre. Vous trouverez ci-dessous quelques notions de base concernant les nombres négatifs. Pour plus d'informations, consultez nos articles sur l'ajout et la soustraction de nombres négatifs et la division et la multiplication des nombres négatifs.
3 Savoir utiliser des nombres négatifs. En algèbre, il est courant d'utiliser des nombres négatifs, il est donc judicieux d'examiner comment ajouter, soustraire, multiplier et diviser les négatifs avant de commencer à apprendre l'algèbre. Vous trouverez ci-dessous quelques notions de base concernant les nombres négatifs. Pour plus d'informations, consultez nos articles sur l'ajout et la soustraction de nombres négatifs et la division et la multiplication des nombres négatifs.  4 Savoir organiser de longs problèmes. Bien que les problèmes simples d'algèbre puissent être résolus, des problèmes plus complexes peuvent nécessiter de nombreuses étapes. Pour éviter les erreurs, organisez votre travail en commençant une nouvelle ligne chaque fois que vous franchissez une étape vers la résolution de votre problème. Si vous avez affaire à une équation à deux côtés, essayez d'écrire tous les signes égaux ("=" s) les uns en dessous des autres. De cette façon, si vous faites une erreur quelque part, ce sera beaucoup plus facile à trouver et à corriger.
4 Savoir organiser de longs problèmes. Bien que les problèmes simples d'algèbre puissent être résolus, des problèmes plus complexes peuvent nécessiter de nombreuses étapes. Pour éviter les erreurs, organisez votre travail en commençant une nouvelle ligne chaque fois que vous franchissez une étape vers la résolution de votre problème. Si vous avez affaire à une équation à deux côtés, essayez d'écrire tous les signes égaux ("=" s) les uns en dessous des autres. De cette façon, si vous faites une erreur quelque part, ce sera beaucoup plus facile à trouver et à corriger.  1 Recherchez les symboles qui ne sont pas des nombres. En algèbre, vous commencerez à voir des lettres et des symboles apparaître dans vos problèmes mathématiques, plutôt que de simples chiffres. Ce sont des variables. Les variables ne sont pas aussi déroutantes qu’elles peuvent paraître au premier abord - ce ne sont que des moyens de montrer des nombres avec des valeurs inconnues. Vous trouverez ci-dessous quelques exemples courants de variables en algèbre:
1 Recherchez les symboles qui ne sont pas des nombres. En algèbre, vous commencerez à voir des lettres et des symboles apparaître dans vos problèmes mathématiques, plutôt que de simples chiffres. Ce sont des variables. Les variables ne sont pas aussi déroutantes qu’elles peuvent paraître au premier abord - ce ne sont que des moyens de montrer des nombres avec des valeurs inconnues. Vous trouverez ci-dessous quelques exemples courants de variables en algèbre:  2 Pensez aux variables comme des nombres "inconnus". Comme mentionné ci-dessus, les variables sont essentiellement des nombres avec des valeurs inconnues. En d'autres termes, il y a un certain nombre cela peut aller à la place de la variable pour faire fonctionner l'équation. Généralement, votre objectif dans un problème d'algèbre est de déterminer quelle est la variable - considérez-la comme un "numéro mystère" que vous essayez de découvrir.
2 Pensez aux variables comme des nombres "inconnus". Comme mentionné ci-dessus, les variables sont essentiellement des nombres avec des valeurs inconnues. En d'autres termes, il y a un certain nombre cela peut aller à la place de la variable pour faire fonctionner l'équation. Généralement, votre objectif dans un problème d'algèbre est de déterminer quelle est la variable - considérez-la comme un "numéro mystère" que vous essayez de découvrir.  3 Surveillez les variables récurrentes. Si une variable apparaît plus d'une fois, simplifiez les variables. Que faites-vous si la même variable apparaît plus d'une fois dans l'équation? Bien que cette situation puisse sembler délicate à résoudre, vous pouvez réellement traiter les variables comme vous traitez les nombres normaux - en d'autres termes, vous pouvez les ajouter, les soustraire, etc., tant que vous ne combinez que des variables identiques. En d'autres termes, x + x = 2x, mais x + y n'est pas égal à 2xy.
3 Surveillez les variables récurrentes. Si une variable apparaît plus d'une fois, simplifiez les variables. Que faites-vous si la même variable apparaît plus d'une fois dans l'équation? Bien que cette situation puisse sembler délicate à résoudre, vous pouvez réellement traiter les variables comme vous traitez les nombres normaux - en d'autres termes, vous pouvez les ajouter, les soustraire, etc., tant que vous ne combinez que des variables identiques. En d'autres termes, x + x = 2x, mais x + y n'est pas égal à 2xy.  1 Essayez d'obtenir la variable par elle-même dans les équations algébriques. Résoudre une équation en algèbre signifie généralement découvrir quelle est la variable. Les équations algébriques sont généralement configurées avec des nombres et / ou des variables des deux côtés, comme ceci: x + 2 = 9 × 4. Pour déterminer quelle est la variable, vous devez l'obtenir seule d'un côté du signe égal. Tout ce qui reste de l'autre côté du signe égal est votre réponse.
1 Essayez d'obtenir la variable par elle-même dans les équations algébriques. Résoudre une équation en algèbre signifie généralement découvrir quelle est la variable. Les équations algébriques sont généralement configurées avec des nombres et / ou des variables des deux côtés, comme ceci: x + 2 = 9 × 4. Pour déterminer quelle est la variable, vous devez l'obtenir seule d'un côté du signe égal. Tout ce qui reste de l'autre côté du signe égal est votre réponse.  2 Annuler l'addition avec soustraction (et vice versa). Comme nous venons de le voir ci-dessus, obtenir x par lui-même d'un côté du signe égal signifie généralement se débarrasser des nombres à côté. Pour ce faire, nous effectuons l'opération "opposée" des deux côtés de l'équation. Par exemple, dans l'équation x + 3 = 0, puisque nous voyons un "+ 3" à côté de notre x, nous placerons un "- 3" des deux côtés. Le "+ 3" et "- 3", laissant x par lui-même et "-3" de l'autre côté du signe égal, comme ceci: x = -3.
2 Annuler l'addition avec soustraction (et vice versa). Comme nous venons de le voir ci-dessus, obtenir x par lui-même d'un côté du signe égal signifie généralement se débarrasser des nombres à côté. Pour ce faire, nous effectuons l'opération "opposée" des deux côtés de l'équation. Par exemple, dans l'équation x + 3 = 0, puisque nous voyons un "+ 3" à côté de notre x, nous placerons un "- 3" des deux côtés. Le "+ 3" et "- 3", laissant x par lui-même et "-3" de l'autre côté du signe égal, comme ceci: x = -3.  3 Annuler la multiplication avec division (et vice versa). La multiplication et la division sont un peu plus difficiles à travailler que l'addition et la soustraction, mais elles ont la même relation "opposée". Si vous voyez un "× 3" sur un côté, vous l’annulerez en divisant les deux côtés par 3, et ainsi de suite.
3 Annuler la multiplication avec division (et vice versa). La multiplication et la division sont un peu plus difficiles à travailler que l'addition et la soustraction, mais elles ont la même relation "opposée". Si vous voyez un "× 3" sur un côté, vous l’annulerez en divisant les deux côtés par 3, et ainsi de suite.  4 Annulez les exposants en prenant la racine (et vice versa). Les exposants sont un sujet de pré-algèbre assez avancé - si vous ne savez pas comment les faire, consultez notre article exposant de base pour plus d'informations. Le "contraire" d'un exposant est la racine qui a le même nombre que lui. Par exemple, le contraire du 2 l'exposant est une racine carrée (√), l'opposé du 3 exposant est la racine du cube (3√), et ainsi de suite.
4 Annulez les exposants en prenant la racine (et vice versa). Les exposants sont un sujet de pré-algèbre assez avancé - si vous ne savez pas comment les faire, consultez notre article exposant de base pour plus d'informations. Le "contraire" d'un exposant est la racine qui a le même nombre que lui. Par exemple, le contraire du 2 l'exposant est une racine carrée (√), l'opposé du 3 exposant est la racine du cube (3√), et ainsi de suite.  1 Utilisez des images pour clarifier les problèmes. Si vous éprouvez de la difficulté à visualiser un problème d'algèbre, essayez d'utiliser des diagrammes ou des images pour illustrer votre équation. Vous pouvez même essayer d'utiliser un groupe d'objets physiques (comme des blocs ou des pièces de monnaie) à la place si vous en avez à portée de main.
1 Utilisez des images pour clarifier les problèmes. Si vous éprouvez de la difficulté à visualiser un problème d'algèbre, essayez d'utiliser des diagrammes ou des images pour illustrer votre équation. Vous pouvez même essayer d'utiliser un groupe d'objets physiques (comme des blocs ou des pièces de monnaie) à la place si vous en avez à portée de main.  2 Utilisez des "tests de bon sens" (en particulier pour les problèmes de mots). Lorsque vous convertissez un problème de mot en algèbre, essayez de vérifier votre formule en connectant des valeurs simples à votre variable. Est-ce que votre équation a du sens quand x = 0? Quand x = 1? Quand x = -1? Il est facile de faire des erreurs simples en écrivant p = 6d quand vous parlez de p = d / 6, mais ces erreurs sont facilement détectées si vous faites une vérification rapide de votre travail avant d'aller plus loin.
2 Utilisez des "tests de bon sens" (en particulier pour les problèmes de mots). Lorsque vous convertissez un problème de mot en algèbre, essayez de vérifier votre formule en connectant des valeurs simples à votre variable. Est-ce que votre équation a du sens quand x = 0? Quand x = 1? Quand x = -1? Il est facile de faire des erreurs simples en écrivant p = 6d quand vous parlez de p = d / 6, mais ces erreurs sont facilement détectées si vous faites une vérification rapide de votre travail avant d'aller plus loin.  3 Sachez que les réponses ne seront pas toujours des nombres entiers en algèbre. Les réponses en algèbre et les autres formes avancées de mathématiques ne sont pas toujours des nombres simples et ronds. Ils peuvent souvent être des nombres décimaux, des fractions ou des nombres irrationnels. Une calculatrice peut vous aider à trouver ces réponses compliquées, mais gardez à l'esprit que votre professeur peut vous demander de donner votre réponse sous sa forme exacte, et non avec une décimale lourde.
3 Sachez que les réponses ne seront pas toujours des nombres entiers en algèbre. Les réponses en algèbre et les autres formes avancées de mathématiques ne sont pas toujours des nombres simples et ronds. Ils peuvent souvent être des nombres décimaux, des fractions ou des nombres irrationnels. Une calculatrice peut vous aider à trouver ces réponses compliquées, mais gardez à l'esprit que votre professeur peut vous demander de donner votre réponse sous sa forme exacte, et non avec une décimale lourde.  4 Essayez d'étendre vos compétences. Lorsque vous êtes en confiance avec l'algèbre de base, essayez la factorisation. L'une des compétences les plus délicates en algèbre est la factorisation - une sorte de raccourci pour obtenir des équations complexes dans des formes simples. L'affacturage est un sujet d'algèbre semi-avancé, alors pensez à consulter l'article lié ci-dessus si vous avez des difficultés à le maîtriser. Vous trouverez ci-dessous quelques astuces pour la factorisation des équations:
4 Essayez d'étendre vos compétences. Lorsque vous êtes en confiance avec l'algèbre de base, essayez la factorisation. L'une des compétences les plus délicates en algèbre est la factorisation - une sorte de raccourci pour obtenir des équations complexes dans des formes simples. L'affacturage est un sujet d'algèbre semi-avancé, alors pensez à consulter l'article lié ci-dessus si vous avez des difficultés à le maîtriser. Vous trouverez ci-dessous quelques astuces pour la factorisation des équations:  5 Pratique, pratique, pratique! Les progrès en algèbre (et tout autre type de mathématiques) exigent beaucoup de travail et de répétition. Ne vous inquiétez pas - en faisant attention en classe, en effectuant toutes vos tâches et en cherchant de l'aide auprès de votre enseignant ou d'autres élèves quand vous en avez besoin, l'algèbre va commencer à devenir une seconde nature.
5 Pratique, pratique, pratique! Les progrès en algèbre (et tout autre type de mathématiques) exigent beaucoup de travail et de répétition. Ne vous inquiétez pas - en faisant attention en classe, en effectuant toutes vos tâches et en cherchant de l'aide auprès de votre enseignant ou d'autres élèves quand vous en avez besoin, l'algèbre va commencer à devenir une seconde nature.  6 Demandez à votre professeur de vous aider à comprendre les sujets délicats de l’algèbre. Si vous avez du mal à maîtriser l'algèbre, ne vous inquiétez pas, vous n'avez pas à l'apprendre par vous-même. Votre enseignant est la première personne à laquelle vous devez vous adresser avec des questions. Après le cours, demandez poliment à votre professeur de vous aider. Les bons enseignants seront généralement disposés à ré-expliquer le sujet de la journée lors d'un rendez-vous après l'école et peuvent même être en mesure de vous donner du matériel de pratique supplémentaire.
6 Demandez à votre professeur de vous aider à comprendre les sujets délicats de l’algèbre. Si vous avez du mal à maîtriser l'algèbre, ne vous inquiétez pas, vous n'avez pas à l'apprendre par vous-même. Votre enseignant est la première personne à laquelle vous devez vous adresser avec des questions. Après le cours, demandez poliment à votre professeur de vous aider. Les bons enseignants seront généralement disposés à ré-expliquer le sujet de la journée lors d'un rendez-vous après l'école et peuvent même être en mesure de vous donner du matériel de pratique supplémentaire.  1 Apprenez à représenter graphiquement les équations x / y. Les graphes peuvent être des outils précieux en algèbre car ils vous permettent d'afficher des idées pour lesquelles vous avez généralement besoin de chiffres dans des images faciles à comprendre. En général, en algèbre, les problèmes graphiques se limitent à des équations à deux variables (généralement x et y) et se font sur un simple graphique à deux dimensions avec un axe x et un axe y. Avec ces équations, tout ce que vous avez à faire est de brancher une valeur pour x, puis de résoudre y (ou de faire l'inverse) pour obtenir deux nombres correspondant à un point du graphique.
1 Apprenez à représenter graphiquement les équations x / y. Les graphes peuvent être des outils précieux en algèbre car ils vous permettent d'afficher des idées pour lesquelles vous avez généralement besoin de chiffres dans des images faciles à comprendre. En général, en algèbre, les problèmes graphiques se limitent à des équations à deux variables (généralement x et y) et se font sur un simple graphique à deux dimensions avec un axe x et un axe y. Avec ces équations, tout ce que vous avez à faire est de brancher une valeur pour x, puis de résoudre y (ou de faire l'inverse) pour obtenir deux nombres correspondant à un point du graphique.  2 Apprenez à résoudre les inégalités. Que faites-vous quand votre équation n'utilise pas un signe égal? Rien de bien différent de ce que vous feriez normalement, il s'avère que Pour les inégalités, qui utilisent des signes comme> ("supérieur à") et <("inférieur à"), résolvez simplement comme d'habitude. Vous serez laissé avec une réponse qui est soit inférieure ou supérieure à votre variable.
2 Apprenez à résoudre les inégalités. Que faites-vous quand votre équation n'utilise pas un signe égal? Rien de bien différent de ce que vous feriez normalement, il s'avère que Pour les inégalités, qui utilisent des signes comme> ("supérieur à") et <("inférieur à"), résolvez simplement comme d'habitude. Vous serez laissé avec une réponse qui est soit inférieure ou supérieure à votre variable.  3 S'attaquer aux équations quadratiques. Un sujet d'algèbre avec lequel beaucoup de débutants luttent est la résolution d'équations quadratiques. Les quadratiques sont des équations avec la forme ax2 + bx + c = 0, où a, b et c sont des nombres (sauf que a ne peut pas être 0.) Ces équations sont résolues avec la formule x = [-b +/- √ (b2 - 4ac)] / 2a. Faites attention - le signe +/- signifie que vous devez trouver les réponses pour ajouter et soustraire, de sorte que vous pouvez avoir deux réponses à ces types de problèmes.
3 S'attaquer aux équations quadratiques. Un sujet d'algèbre avec lequel beaucoup de débutants luttent est la résolution d'équations quadratiques. Les quadratiques sont des équations avec la forme ax2 + bx + c = 0, où a, b et c sont des nombres (sauf que a ne peut pas être 0.) Ces équations sont résolues avec la formule x = [-b +/- √ (b2 - 4ac)] / 2a. Faites attention - le signe +/- signifie que vous devez trouver les réponses pour ajouter et soustraire, de sorte que vous pouvez avoir deux réponses à ces types de problèmes. 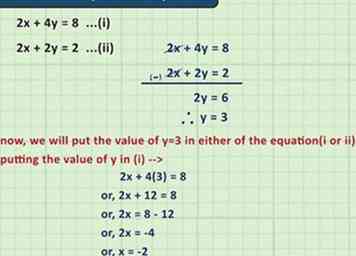 4 Expérimentez avec des systèmes d'équations. Résoudre plus d'une équation à la fois peut sembler super difficile, mais lorsque vous travaillez avec des équations d'algèbre simples, ce n'est pas si difficile. Les enseignants d'algèbre utilisent souvent une approche graphique pour résoudre ces problèmes. Lorsque vous travaillez avec un système de deux équations, les solutions sont les points sur un graphique auxquels les lignes des deux équations se croisent.
4 Expérimentez avec des systèmes d'équations. Résoudre plus d'une équation à la fois peut sembler super difficile, mais lorsque vous travaillez avec des équations d'algèbre simples, ce n'est pas si difficile. Les enseignants d'algèbre utilisent souvent une approche graphique pour résoudre ces problèmes. Lorsque vous travaillez avec un système de deux équations, les solutions sont les points sur un graphique auxquels les lignes des deux équations se croisent.