Bien qu'il soit facile de commander des nombres entiers comme 1, 3 et 8 par taille, les fractions peuvent être difficiles à mesurer en un coup d'œil. Si chaque nombre ou dénominateur inférieur est identique, vous pouvez les commander comme des nombres entiers, par exemple 1/5, 3/5 et 8/5. Sinon, vous pouvez modifier votre liste de fractions pour utiliser le même dénominateur, sans modifier la taille d'aucune fraction. Cela devient plus facile avec la pratique, et vous pouvez aussi apprendre quelques "trucs" lorsque vous comparez seulement deux fractions, ou lorsque vous triez des fractions "impropres" comme 7/3.
Méthode One of Three:
Commander n'importe quel nombre de fractions
-
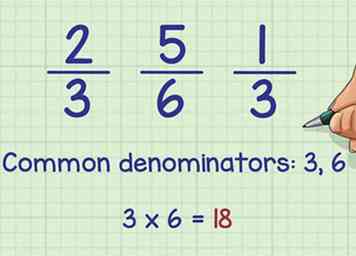 1 Trouvez un dénominateur commun pour toutes les fractions. Utilisez l'une de ces méthodes pour trouver un dénominateur ou un nombre inférieur de fraction que vous pouvez utiliser pour réécrire chaque fraction de la liste afin de pouvoir les comparer facilement. Ceci s'appelle un dénominateur commun, ou la plus petit dénominateur commun si c'est le plus bas possible:[1]
1 Trouvez un dénominateur commun pour toutes les fractions. Utilisez l'une de ces méthodes pour trouver un dénominateur ou un nombre inférieur de fraction que vous pouvez utiliser pour réécrire chaque fraction de la liste afin de pouvoir les comparer facilement. Ceci s'appelle un dénominateur commun, ou la plus petit dénominateur commun si c'est le plus bas possible:[1] - Multipliez tous les dénominateurs différents ensemble. Par exemple, si vous comparez 2/3, 5/6 et 1/3, multipliez les deux dénominateurs différents: 3 x 6 = 18. Ceci est une méthode simple, mais aboutira souvent à un nombre beaucoup plus important que les autres méthodes, ce qui peut être difficile à utiliser.
- Ou énumérer les multiples de chaque dénominateur dans une colonne distincte, jusqu'à ce que vous remarquiez un nombre qui apparaît sur chaque colonne. Utilisez ce numéro. Par exemple, en comparant 2/3, 5/6 et 1/3, indiquez quelques multiples de 3: 3, 6, 9, 12, 15, 18. Puis listez les multiples de 6: 6, 12, 18. Depuis 18 apparaît sur les deux listes, utilisez ce numéro. (Vous pouvez également utiliser 12, mais les exemples ci-dessous supposent que vous utilisez 18.)
-
 2 Convertissez chaque fraction pour qu'elle utilise le dénominateur commun. N'oubliez pas que si vous multipliez le haut et le bas d'une fraction par la même quantité, la fraction a toujours la même taille. Utilisez cette technique sur chaque fraction, une par une, de sorte que chacune utilise le dénominateur commun comme nombre inférieur. Essayez-le pour 2/3, 5/6 et 1/3, en utilisant le dénominateur commun 18:
2 Convertissez chaque fraction pour qu'elle utilise le dénominateur commun. N'oubliez pas que si vous multipliez le haut et le bas d'une fraction par la même quantité, la fraction a toujours la même taille. Utilisez cette technique sur chaque fraction, une par une, de sorte que chacune utilise le dénominateur commun comme nombre inférieur. Essayez-le pour 2/3, 5/6 et 1/3, en utilisant le dénominateur commun 18: - 18 ÷ 3 = 6, donc 2/3 = (2x6) / (3x6) = 12/18
- 18 ÷ 6 = 3, donc 5/6 = (5x3) / (6x3) = 15/18
- 18 ÷ 3 = 6, donc 1/3 = (1x6) / (3x6) = 6/18
-
 3 Utilisez le numéro du haut pour commander les fractions. Maintenant qu'ils ont tous le même dénominateur, les fractions sont faciles à comparer. Utilisez leur numéro supérieur ou numérateur, pour les classer du moins au plus grand. En classant les fractions que nous avons trouvées ci-dessus, nous obtenons: 6/18, 12/18, 15/18.
3 Utilisez le numéro du haut pour commander les fractions. Maintenant qu'ils ont tous le même dénominateur, les fractions sont faciles à comparer. Utilisez leur numéro supérieur ou numérateur, pour les classer du moins au plus grand. En classant les fractions que nous avons trouvées ci-dessus, nous obtenons: 6/18, 12/18, 15/18. -
 4 Renvoyez chaque fraction à sa forme originale. Gardez les fractions dans le même ordre, mais remettez-les dans leur forme d'origine. Vous pouvez le faire en vous rappelant comment chaque fraction a été transformée ou en divisant à nouveau le haut et le bas de chaque fraction:
4 Renvoyez chaque fraction à sa forme originale. Gardez les fractions dans le même ordre, mais remettez-les dans leur forme d'origine. Vous pouvez le faire en vous rappelant comment chaque fraction a été transformée ou en divisant à nouveau le haut et le bas de chaque fraction: - 6/18 = (6 ÷ 6)/(18 ÷ 6) = 1/3
- 12/18 = (12 ÷ 6)/(18 ÷ 6) = 2/3
- 15/18 = (15 ÷ 3)/(18 ÷ 3) = 5/6
- La réponse est "1/3, 2/3, 5/6"
Méthode deux sur trois:
Ordonner deux fractions en utilisant la multiplication croisée
-
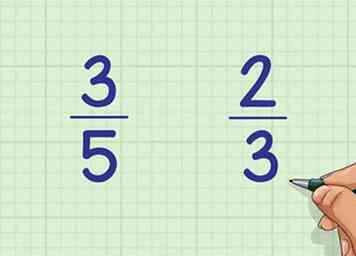 1 Écrivez les deux fractions l'une à côté de l'autre. Par exemple, comparez la fraction 3/5 et la fraction 2/3. Écrivez-les côte à côte sur la page: 3/5 à gauche et 2/3 à droite.
1 Écrivez les deux fractions l'une à côté de l'autre. Par exemple, comparez la fraction 3/5 et la fraction 2/3. Écrivez-les côte à côte sur la page: 3/5 à gauche et 2/3 à droite. -
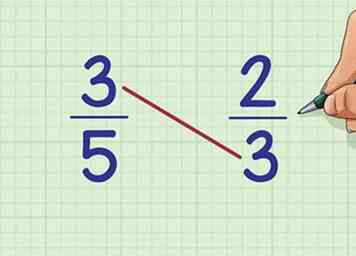 2 Multipliez le haut de la première fraction avec le bas de la deuxième fraction. Dans notre exemple, le numéro supérieur ou numérateur, de la première fraction (3/5) est 3. Le nombre inférieur, ou dénominateur, de la deuxième fraction (2/3) est aussi 3. Multipliez-les ensemble: 3 x 3 =?
2 Multipliez le haut de la première fraction avec le bas de la deuxième fraction. Dans notre exemple, le numéro supérieur ou numérateur, de la première fraction (3/5) est 3. Le nombre inférieur, ou dénominateur, de la deuxième fraction (2/3) est aussi 3. Multipliez-les ensemble: 3 x 3 =? - Cette méthode s'appelle multiplication croisée, car vous multipliez les nombres en diagonale les uns par rapport aux autres.
-
 3 Écrivez votre réponse à côté de la première fraction. Écrivez le produit ou répondez à votre problème de multiplication à côté de la première fraction de la page. Dans notre exemple, 3 x 3 = 9, vous écrivez donc 9 à côté de la première fraction, sur le côté gauche de la page.
3 Écrivez votre réponse à côté de la première fraction. Écrivez le produit ou répondez à votre problème de multiplication à côté de la première fraction de la page. Dans notre exemple, 3 x 3 = 9, vous écrivez donc 9 à côté de la première fraction, sur le côté gauche de la page. -
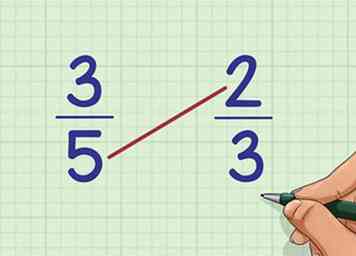 4 Multipliez le haut de la seconde fraction avec le bas de la premier. Pour déterminer quelle fraction est la plus grande, nous devons comparer notre réponse ci-dessus avec la réponse à un autre problème de multiplication. Multipliez ces deux nombres ensemble. Pour notre exemple (en comparant 3/5 et 2/3), multipliez 2 x 5 ensemble.
4 Multipliez le haut de la seconde fraction avec le bas de la premier. Pour déterminer quelle fraction est la plus grande, nous devons comparer notre réponse ci-dessus avec la réponse à un autre problème de multiplication. Multipliez ces deux nombres ensemble. Pour notre exemple (en comparant 3/5 et 2/3), multipliez 2 x 5 ensemble. -
 5 Ecrivez cette réponse à côté de la deuxième fraction. Écrivez la réponse à ce deuxième problème de multiplication à côté de la deuxième fraction. Dans cet exemple, la réponse est 10.
5 Ecrivez cette réponse à côté de la deuxième fraction. Écrivez la réponse à ce deuxième problème de multiplication à côté de la deuxième fraction. Dans cet exemple, la réponse est 10. -
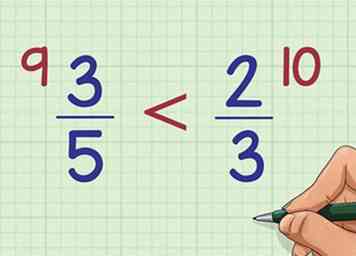 6 Comparez les valeurs des deux produits croisés. Les réponses aux problèmes de multiplication dans cette méthode sont appelées produits croisés. Si un produit croisé est plus grand que l'autre, la fraction à côté de ce produit croisé est également plus grande que l'autre fraction. Dans notre exemple, car 9 est inférieur à 10, cela signifie que 3/5 doit être inférieur à 2/3.
6 Comparez les valeurs des deux produits croisés. Les réponses aux problèmes de multiplication dans cette méthode sont appelées produits croisés. Si un produit croisé est plus grand que l'autre, la fraction à côté de ce produit croisé est également plus grande que l'autre fraction. Dans notre exemple, car 9 est inférieur à 10, cela signifie que 3/5 doit être inférieur à 2/3. - Rappelez-vous, écrivez toujours le produit croisé à côté de la fraction dont Haut numéro que vous avez utilisé.
-
 7 Comprenez pourquoi cela fonctionne. Pour comparer deux fractions, vous les transformez généralement pour leur donner le même dénominateur, ou la partie inférieure de la fraction. Secrètement, c'est ce que fait la multiplication croisée![2] Il ignore simplement l'écriture des dénominateurs, car une fois que les deux fractions sont identiques, il suffit de comparer les deux premiers nombres. Voici notre même exemple (3/5 vs 2/3), écrit sans la multiplication croisée "raccourci":
7 Comprenez pourquoi cela fonctionne. Pour comparer deux fractions, vous les transformez généralement pour leur donner le même dénominateur, ou la partie inférieure de la fraction. Secrètement, c'est ce que fait la multiplication croisée![2] Il ignore simplement l'écriture des dénominateurs, car une fois que les deux fractions sont identiques, il suffit de comparer les deux premiers nombres. Voici notre même exemple (3/5 vs 2/3), écrit sans la multiplication croisée "raccourci": - 3/5 = (3x3) / (5x3) = 9/15
- 2/3 = (2x5) / (3x5) = 10/15
- 9/15 est inférieur à 10/15
- Par conséquent, 3/5 est inférieur à 2/3
Méthode trois sur trois:
Commander des fractions plus grandes qu'une
-
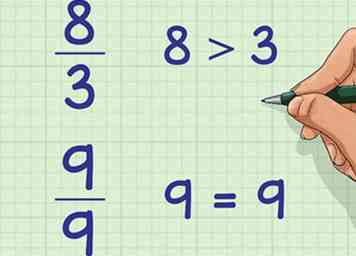 1 Utilisez cette option pour les fractions avec un nombre supérieur égal ou supérieur au nombre inférieur. Si une fraction a un numéro supérieur, ou numérateur, qui est plus grand que le nombre inférieur, ou dénominateur, il est plus grand qu'un.8/3 est un exemple de ce type de fraction. Vous pouvez également l'utiliser pour les fractions avec un numérateur et un dénominateur égaux, tels que 9/9. Ces deux fractions sont des exemples de fractions impropres.[3]
1 Utilisez cette option pour les fractions avec un nombre supérieur égal ou supérieur au nombre inférieur. Si une fraction a un numéro supérieur, ou numérateur, qui est plus grand que le nombre inférieur, ou dénominateur, il est plus grand qu'un.8/3 est un exemple de ce type de fraction. Vous pouvez également l'utiliser pour les fractions avec un numérateur et un dénominateur égaux, tels que 9/9. Ces deux fractions sont des exemples de fractions impropres.[3] - Vous pouvez toujours utiliser les autres méthodes pour ces fractions. Cette méthode aide ces fractions à avoir du sens, et pourrait être plus rapide.
-
 2 Convertir chaque fraction impropre en un nombre mixte. Transformez-les en un mélange de nombres entiers et de fractions. Parfois, vous pouvez le faire dans votre tête. Par exemple, 9/9 = 1. D'autres fois, utilisez la division longue pour savoir combien de fois le numérateur va uniformément dans le dénominateur. Le reste de ce problème de longue division, s'il y en a un, reste "en suspens" en tant que fraction. Par exemple:
2 Convertir chaque fraction impropre en un nombre mixte. Transformez-les en un mélange de nombres entiers et de fractions. Parfois, vous pouvez le faire dans votre tête. Par exemple, 9/9 = 1. D'autres fois, utilisez la division longue pour savoir combien de fois le numérateur va uniformément dans le dénominateur. Le reste de ce problème de longue division, s'il y en a un, reste "en suspens" en tant que fraction. Par exemple: - 8/3 = 2 + 2/3
- 9/9 = 1
- 19/4 = 4 + 3/4
- 13/6 = 2 + 1/6
-
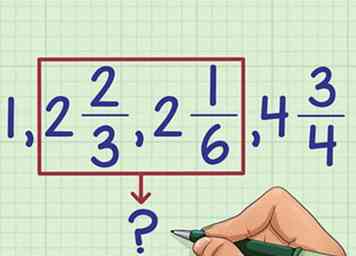 3 Trier les nombres mixtes par nombre entier. Maintenant qu'il n'y a plus de fractions impropres, vous avez une meilleure idée de la taille de chaque nombre. Ignorez les fractions pour le moment et triez les fractions en groupes par nombre entier:
3 Trier les nombres mixtes par nombre entier. Maintenant qu'il n'y a plus de fractions impropres, vous avez une meilleure idée de la taille de chaque nombre. Ignorez les fractions pour le moment et triez les fractions en groupes par nombre entier: - 1 est le plus petit
- 2 + 2/3 et 2 + 1/6 (on ne sait pas encore ce qui est plus grand que l'autre)
- 4 + 3/4 est le plus grand
-
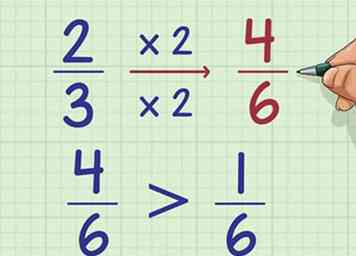 4 Si nécessaire, comparez les fractions de chaque groupe. Si vous avez plusieurs nombres mélangés avec le même nombre entier, tels que 2 + 2/3 et 2 + 1/6, comparez la fraction du nombre pour voir lequel est le plus grand. Pour ce faire, vous pouvez utiliser l'une des méthodes décrites dans les autres sections. Voici un exemple comparant 2 + 2/3 et 2 + 1/6, convertissant les fractions au même dénominateur:
4 Si nécessaire, comparez les fractions de chaque groupe. Si vous avez plusieurs nombres mélangés avec le même nombre entier, tels que 2 + 2/3 et 2 + 1/6, comparez la fraction du nombre pour voir lequel est le plus grand. Pour ce faire, vous pouvez utiliser l'une des méthodes décrites dans les autres sections. Voici un exemple comparant 2 + 2/3 et 2 + 1/6, convertissant les fractions au même dénominateur: - 2/3 = (2x2) / (3x2) = 4/6
- 1/6 = 1/6
- 4/6 est supérieur à 1/6
- 2 + 4/6 est supérieur à 2 + 1/6
- 2 + 2/3 est supérieur à 2 + 1/6
-
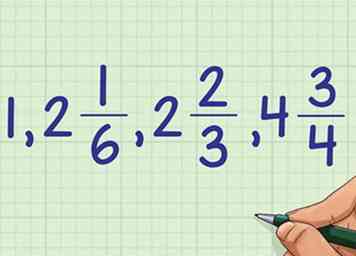 5 Utilisez vos résultats pour trier toute votre liste de nombres mélangés. Une fois que vous avez trié les fractions dans chaque groupe de nombres mélangés, vous pouvez trier votre liste entière: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.
5 Utilisez vos résultats pour trier toute votre liste de nombres mélangés. Une fois que vous avez trié les fractions dans chaque groupe de nombres mélangés, vous pouvez trier votre liste entière: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4. -
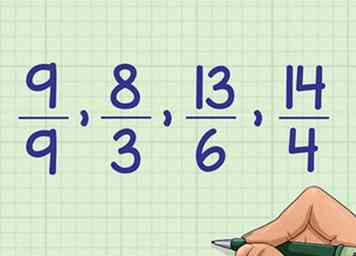 6 Convertir les nombres mélangés à leurs fractions originales. Gardez la même commande, mais annulez les modifications que vous avez apportées et écrivez les nombres comme les fractions originales impropres: 9/9, 8/3, 13/6, 19/4.
6 Convertir les nombres mélangés à leurs fractions originales. Gardez la même commande, mais annulez les modifications que vous avez apportées et écrivez les nombres comme les fractions originales impropres: 9/9, 8/3, 13/6, 19/4.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
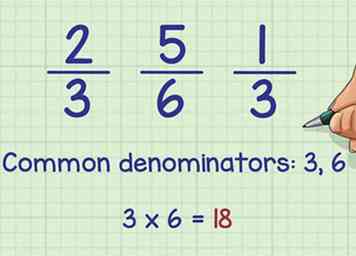 1 Trouvez un dénominateur commun pour toutes les fractions. Utilisez l'une de ces méthodes pour trouver un dénominateur ou un nombre inférieur de fraction que vous pouvez utiliser pour réécrire chaque fraction de la liste afin de pouvoir les comparer facilement. Ceci s'appelle un dénominateur commun, ou la plus petit dénominateur commun si c'est le plus bas possible:[1]
1 Trouvez un dénominateur commun pour toutes les fractions. Utilisez l'une de ces méthodes pour trouver un dénominateur ou un nombre inférieur de fraction que vous pouvez utiliser pour réécrire chaque fraction de la liste afin de pouvoir les comparer facilement. Ceci s'appelle un dénominateur commun, ou la plus petit dénominateur commun si c'est le plus bas possible:[1]  2 Convertissez chaque fraction pour qu'elle utilise le dénominateur commun. N'oubliez pas que si vous multipliez le haut et le bas d'une fraction par la même quantité, la fraction a toujours la même taille. Utilisez cette technique sur chaque fraction, une par une, de sorte que chacune utilise le dénominateur commun comme nombre inférieur. Essayez-le pour 2/3, 5/6 et 1/3, en utilisant le dénominateur commun 18:
2 Convertissez chaque fraction pour qu'elle utilise le dénominateur commun. N'oubliez pas que si vous multipliez le haut et le bas d'une fraction par la même quantité, la fraction a toujours la même taille. Utilisez cette technique sur chaque fraction, une par une, de sorte que chacune utilise le dénominateur commun comme nombre inférieur. Essayez-le pour 2/3, 5/6 et 1/3, en utilisant le dénominateur commun 18:  3 Utilisez le numéro du haut pour commander les fractions. Maintenant qu'ils ont tous le même dénominateur, les fractions sont faciles à comparer. Utilisez leur numéro supérieur ou numérateur, pour les classer du moins au plus grand. En classant les fractions que nous avons trouvées ci-dessus, nous obtenons: 6/18, 12/18, 15/18.
3 Utilisez le numéro du haut pour commander les fractions. Maintenant qu'ils ont tous le même dénominateur, les fractions sont faciles à comparer. Utilisez leur numéro supérieur ou numérateur, pour les classer du moins au plus grand. En classant les fractions que nous avons trouvées ci-dessus, nous obtenons: 6/18, 12/18, 15/18.  4 Renvoyez chaque fraction à sa forme originale. Gardez les fractions dans le même ordre, mais remettez-les dans leur forme d'origine. Vous pouvez le faire en vous rappelant comment chaque fraction a été transformée ou en divisant à nouveau le haut et le bas de chaque fraction:
4 Renvoyez chaque fraction à sa forme originale. Gardez les fractions dans le même ordre, mais remettez-les dans leur forme d'origine. Vous pouvez le faire en vous rappelant comment chaque fraction a été transformée ou en divisant à nouveau le haut et le bas de chaque fraction: 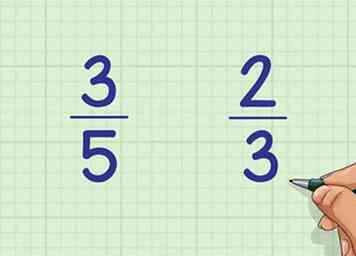 1 Écrivez les deux fractions l'une à côté de l'autre. Par exemple, comparez la fraction 3/5 et la fraction 2/3. Écrivez-les côte à côte sur la page: 3/5 à gauche et 2/3 à droite.
1 Écrivez les deux fractions l'une à côté de l'autre. Par exemple, comparez la fraction 3/5 et la fraction 2/3. Écrivez-les côte à côte sur la page: 3/5 à gauche et 2/3 à droite. 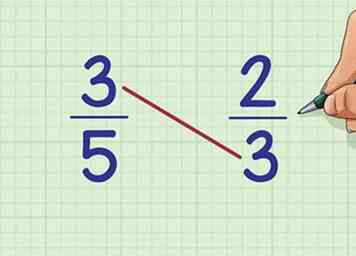 2 Multipliez le haut de la première fraction avec le bas de la deuxième fraction. Dans notre exemple, le numéro supérieur ou numérateur, de la première fraction (3/5) est 3. Le nombre inférieur, ou dénominateur, de la deuxième fraction (2/3) est aussi 3. Multipliez-les ensemble: 3 x 3 =?
2 Multipliez le haut de la première fraction avec le bas de la deuxième fraction. Dans notre exemple, le numéro supérieur ou numérateur, de la première fraction (3/5) est 3. Le nombre inférieur, ou dénominateur, de la deuxième fraction (2/3) est aussi 3. Multipliez-les ensemble: 3 x 3 =?  3 Écrivez votre réponse à côté de la première fraction. Écrivez le produit ou répondez à votre problème de multiplication à côté de la première fraction de la page. Dans notre exemple, 3 x 3 = 9, vous écrivez donc 9 à côté de la première fraction, sur le côté gauche de la page.
3 Écrivez votre réponse à côté de la première fraction. Écrivez le produit ou répondez à votre problème de multiplication à côté de la première fraction de la page. Dans notre exemple, 3 x 3 = 9, vous écrivez donc 9 à côté de la première fraction, sur le côté gauche de la page.  4 Multipliez le haut de la seconde fraction avec le bas de la premier. Pour déterminer quelle fraction est la plus grande, nous devons comparer notre réponse ci-dessus avec la réponse à un autre problème de multiplication. Multipliez ces deux nombres ensemble. Pour notre exemple (en comparant 3/5 et 2/3), multipliez 2 x 5 ensemble.
4 Multipliez le haut de la seconde fraction avec le bas de la premier. Pour déterminer quelle fraction est la plus grande, nous devons comparer notre réponse ci-dessus avec la réponse à un autre problème de multiplication. Multipliez ces deux nombres ensemble. Pour notre exemple (en comparant 3/5 et 2/3), multipliez 2 x 5 ensemble.  5 Ecrivez cette réponse à côté de la deuxième fraction. Écrivez la réponse à ce deuxième problème de multiplication à côté de la deuxième fraction. Dans cet exemple, la réponse est 10.
5 Ecrivez cette réponse à côté de la deuxième fraction. Écrivez la réponse à ce deuxième problème de multiplication à côté de la deuxième fraction. Dans cet exemple, la réponse est 10. 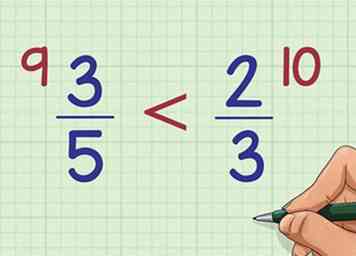 6 Comparez les valeurs des deux produits croisés. Les réponses aux problèmes de multiplication dans cette méthode sont appelées produits croisés. Si un produit croisé est plus grand que l'autre, la fraction à côté de ce produit croisé est également plus grande que l'autre fraction. Dans notre exemple, car 9 est inférieur à 10, cela signifie que 3/5 doit être inférieur à 2/3.
6 Comparez les valeurs des deux produits croisés. Les réponses aux problèmes de multiplication dans cette méthode sont appelées produits croisés. Si un produit croisé est plus grand que l'autre, la fraction à côté de ce produit croisé est également plus grande que l'autre fraction. Dans notre exemple, car 9 est inférieur à 10, cela signifie que 3/5 doit être inférieur à 2/3.  7 Comprenez pourquoi cela fonctionne. Pour comparer deux fractions, vous les transformez généralement pour leur donner le même dénominateur, ou la partie inférieure de la fraction. Secrètement, c'est ce que fait la multiplication croisée![2] Il ignore simplement l'écriture des dénominateurs, car une fois que les deux fractions sont identiques, il suffit de comparer les deux premiers nombres. Voici notre même exemple (3/5 vs 2/3), écrit sans la multiplication croisée "raccourci":
7 Comprenez pourquoi cela fonctionne. Pour comparer deux fractions, vous les transformez généralement pour leur donner le même dénominateur, ou la partie inférieure de la fraction. Secrètement, c'est ce que fait la multiplication croisée![2] Il ignore simplement l'écriture des dénominateurs, car une fois que les deux fractions sont identiques, il suffit de comparer les deux premiers nombres. Voici notre même exemple (3/5 vs 2/3), écrit sans la multiplication croisée "raccourci": 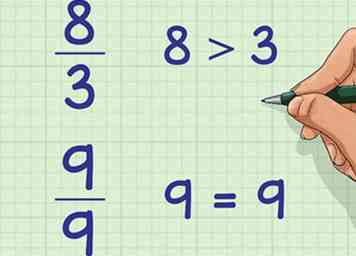 1 Utilisez cette option pour les fractions avec un nombre supérieur égal ou supérieur au nombre inférieur. Si une fraction a un numéro supérieur, ou numérateur, qui est plus grand que le nombre inférieur, ou dénominateur, il est plus grand qu'un.8/3 est un exemple de ce type de fraction. Vous pouvez également l'utiliser pour les fractions avec un numérateur et un dénominateur égaux, tels que 9/9. Ces deux fractions sont des exemples de fractions impropres.[3]
1 Utilisez cette option pour les fractions avec un nombre supérieur égal ou supérieur au nombre inférieur. Si une fraction a un numéro supérieur, ou numérateur, qui est plus grand que le nombre inférieur, ou dénominateur, il est plus grand qu'un.8/3 est un exemple de ce type de fraction. Vous pouvez également l'utiliser pour les fractions avec un numérateur et un dénominateur égaux, tels que 9/9. Ces deux fractions sont des exemples de fractions impropres.[3]  2 Convertir chaque fraction impropre en un nombre mixte. Transformez-les en un mélange de nombres entiers et de fractions. Parfois, vous pouvez le faire dans votre tête. Par exemple, 9/9 = 1. D'autres fois, utilisez la division longue pour savoir combien de fois le numérateur va uniformément dans le dénominateur. Le reste de ce problème de longue division, s'il y en a un, reste "en suspens" en tant que fraction. Par exemple:
2 Convertir chaque fraction impropre en un nombre mixte. Transformez-les en un mélange de nombres entiers et de fractions. Parfois, vous pouvez le faire dans votre tête. Par exemple, 9/9 = 1. D'autres fois, utilisez la division longue pour savoir combien de fois le numérateur va uniformément dans le dénominateur. Le reste de ce problème de longue division, s'il y en a un, reste "en suspens" en tant que fraction. Par exemple: 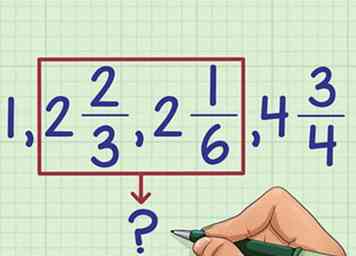 3 Trier les nombres mixtes par nombre entier. Maintenant qu'il n'y a plus de fractions impropres, vous avez une meilleure idée de la taille de chaque nombre. Ignorez les fractions pour le moment et triez les fractions en groupes par nombre entier:
3 Trier les nombres mixtes par nombre entier. Maintenant qu'il n'y a plus de fractions impropres, vous avez une meilleure idée de la taille de chaque nombre. Ignorez les fractions pour le moment et triez les fractions en groupes par nombre entier: 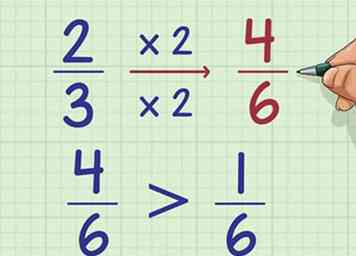 4 Si nécessaire, comparez les fractions de chaque groupe. Si vous avez plusieurs nombres mélangés avec le même nombre entier, tels que 2 + 2/3 et 2 + 1/6, comparez la fraction du nombre pour voir lequel est le plus grand. Pour ce faire, vous pouvez utiliser l'une des méthodes décrites dans les autres sections. Voici un exemple comparant 2 + 2/3 et 2 + 1/6, convertissant les fractions au même dénominateur:
4 Si nécessaire, comparez les fractions de chaque groupe. Si vous avez plusieurs nombres mélangés avec le même nombre entier, tels que 2 + 2/3 et 2 + 1/6, comparez la fraction du nombre pour voir lequel est le plus grand. Pour ce faire, vous pouvez utiliser l'une des méthodes décrites dans les autres sections. Voici un exemple comparant 2 + 2/3 et 2 + 1/6, convertissant les fractions au même dénominateur: 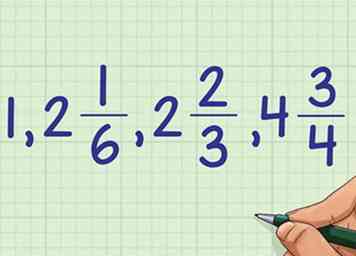 5 Utilisez vos résultats pour trier toute votre liste de nombres mélangés. Une fois que vous avez trié les fractions dans chaque groupe de nombres mélangés, vous pouvez trier votre liste entière: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.
5 Utilisez vos résultats pour trier toute votre liste de nombres mélangés. Une fois que vous avez trié les fractions dans chaque groupe de nombres mélangés, vous pouvez trier votre liste entière: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4. 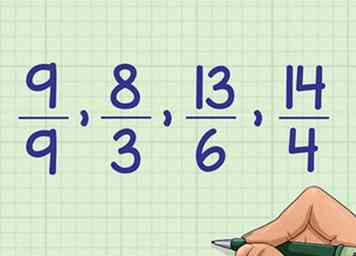 6 Convertir les nombres mélangés à leurs fractions originales. Gardez la même commande, mais annulez les modifications que vous avez apportées et écrivez les nombres comme les fractions originales impropres: 9/9, 8/3, 13/6, 19/4.
6 Convertir les nombres mélangés à leurs fractions originales. Gardez la même commande, mais annulez les modifications que vous avez apportées et écrivez les nombres comme les fractions originales impropres: 9/9, 8/3, 13/6, 19/4.