Pour ajouter ou soustraire des fractions avec des dénominateurs différents (le nombre inférieur de la fraction), vous devez d'abord trouver le plus petit dénominateur commun partagé entre eux. Cela fait référence au plus petit multiple partagé par chaque dénominateur original de l'équation, ou au plus petit nombre entier pouvant être divisé par chaque dénominateur.[1] Vous pouvez également voir l'expression la moins commune multiple. Cela fait généralement référence aux nombres entiers, mais les méthodes pour le trouver sont les mêmes pour les deux. La détermination du plus petit dénominateur commun vous permet de convertir les dénominateurs au même nombre, vous pouvez donc les ajouter et les soustraire.
Méthode One of Four:
Liste de multiples [2]
-
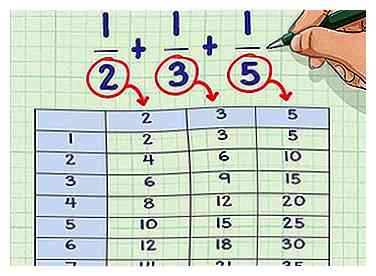 1 Énumérez les multiples de chaque dénominateur. Faites une liste de plusieurs multiples pour chaque dénominateur dans l'équation. Chaque liste doit être composée du nombre de dénominateurs multiplié par 1, 2, 3, 4, etc.
1 Énumérez les multiples de chaque dénominateur. Faites une liste de plusieurs multiples pour chaque dénominateur dans l'équation. Chaque liste doit être composée du nombre de dénominateurs multiplié par 1, 2, 3, 4, etc. - Exemple: 1/2 + 1/3 + 1/5
- Multiples de 2: 2 * 1 = 2; 2 * 2 = 4; 2 * 3 = 6; 2 * 4 = 8; 2 * 5 = 10; 2 * 6 = 12; 2 * 7 = 14; etc.
- Multiples de 3: 3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 * 4 = 12; 3 * 5 = 15; 3 * 6 = 18; 3 * 7 = 21; etc.
- Multiples de 5: 5 * 1 = 5; 5 * 2 = 10; 5 * 3 = 15; 5 * 4 = 20; 5 * 5 = 25; 5 * 6 = 30; 5 * 7 = 35; etc.
-
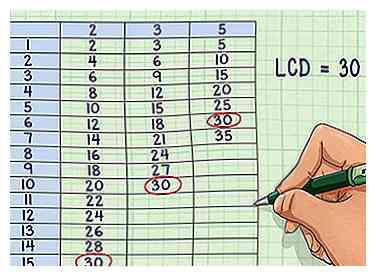 2 Identifier le plus petit multiple commun. Parcourez chaque liste et marquez les multiples qui sont partagés par tous les dénominateurs d'origine. Après avoir identifié les multiples communs, identifiez le plus petit dénominateur.
2 Identifier le plus petit multiple commun. Parcourez chaque liste et marquez les multiples qui sont partagés par tous les dénominateurs d'origine. Après avoir identifié les multiples communs, identifiez le plus petit dénominateur. - Notez que si aucun dénominateur commun n'existe à ce stade, vous devrez peut-être continuer à écrire des multiples jusqu'à ce que vous rencontriez un multiple partagé.
- Cette méthode est plus facile à utiliser lorsque de petits nombres sont présents dans le dénominateur.
- Dans cet exemple, les dénominateurs ne partagent qu'un seul multiple et il est égal à 30: 2 * 15 = 30; 3 * 10 = 30; 5 * 6 = 30
- L'écran LCD = 30
-
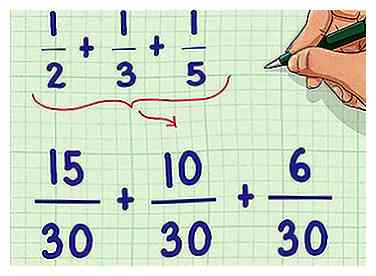 3 Réécrivez l'équation originale. Afin de changer chaque fraction de l'équation pour qu'elle reste fidèle à l'équation d'origine, vous devrez multiplier chaque numérateur (le haut de la fraction) et le dénominateur par le même facteur que celui utilisé pour multiplier le dénominateur correspondant lorsque vous atteignez le LCD.
3 Réécrivez l'équation originale. Afin de changer chaque fraction de l'équation pour qu'elle reste fidèle à l'équation d'origine, vous devrez multiplier chaque numérateur (le haut de la fraction) et le dénominateur par le même facteur que celui utilisé pour multiplier le dénominateur correspondant lorsque vous atteignez le LCD. - Exemple: (15/15) * (1/2); (10/10) * (1/3); (6/6) * (1/5)
- Nouvelle équation: 15/30 + 10/30 + 6/30
-
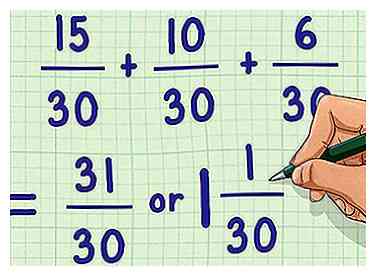 4 Résoudre le problème réécrit. Après avoir trouvé l'écran LCD et modifié les fractions en conséquence, vous devriez pouvoir résoudre le problème sans difficulté supplémentaire. N'oubliez pas de simplifier la fraction à la fin.
4 Résoudre le problème réécrit. Après avoir trouvé l'écran LCD et modifié les fractions en conséquence, vous devriez pouvoir résoudre le problème sans difficulté supplémentaire. N'oubliez pas de simplifier la fraction à la fin. - Exemple: 15/30 + 10/30 + 6/30 = 31/30 = 1 1/30
Méthode deux sur quatre:
Utiliser le plus grand facteur commun [3]
-
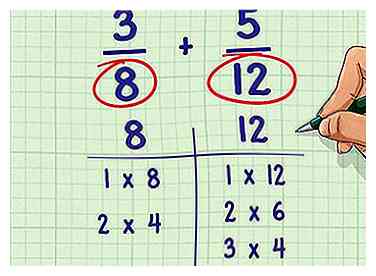 1 Énumérez tous les facteurs de chaque dénominateur. Les facteurs d'un nombre sont tous les nombres entiers qui peuvent être divisés en un seul nombre.[4] Le nombre 6 a quatre facteurs: 6, 3, 2 et 1. Chaque nombre a un facteur de 1 car chaque nombre peut être multiplié par un.
1 Énumérez tous les facteurs de chaque dénominateur. Les facteurs d'un nombre sont tous les nombres entiers qui peuvent être divisés en un seul nombre.[4] Le nombre 6 a quatre facteurs: 6, 3, 2 et 1. Chaque nombre a un facteur de 1 car chaque nombre peut être multiplié par un. - Par exemple: 3/8 + 5/12.
- Facteurs de 8: 1, 2, 4 et 8
- Facteurs de 12: 1, 2, 3, 4, 6, 12
-
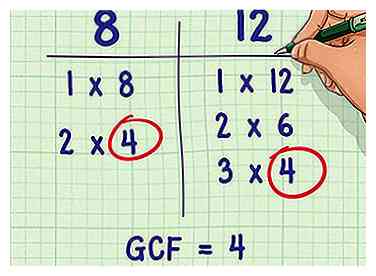 2 Identifier le plus grand facteur commun entre les deux dénominateurs. Une fois que vous avez énuméré les facteurs de chaque dénominateur, encerclez tous les facteurs communs. Le plus grand des facteurs communs est le plus grand facteur commun (GCF) qui sera utilisé pour continuer à résoudre le problème.
2 Identifier le plus grand facteur commun entre les deux dénominateurs. Une fois que vous avez énuméré les facteurs de chaque dénominateur, encerclez tous les facteurs communs. Le plus grand des facteurs communs est le plus grand facteur commun (GCF) qui sera utilisé pour continuer à résoudre le problème. - Dans notre exemple, 8 et 12 partagent les facteurs 1, 2 et 4.
- Le plus grand facteur commun est 4.
-
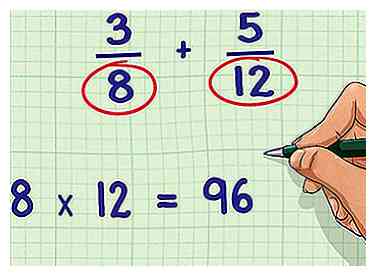 3 Multipliez les dénominateurs ensemble. Afin d'utiliser le plus grand facteur commun pour résoudre le problème, vous devez d'abord multiplier les deux dénominateurs ensemble.
3 Multipliez les dénominateurs ensemble. Afin d'utiliser le plus grand facteur commun pour résoudre le problème, vous devez d'abord multiplier les deux dénominateurs ensemble. - Continuant notre exemple: 8 * 12 = 96
-
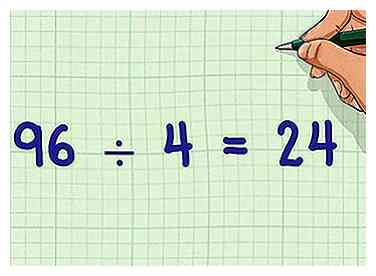 4 Diviser ce produit par le GCF. Après avoir trouvé le produit des deux dénominateurs, divisez ce produit par le GCF que vous avez trouvé précédemment. Ce nombre sera votre plus petit dénominateur commun (LCD).
4 Diviser ce produit par le GCF. Après avoir trouvé le produit des deux dénominateurs, divisez ce produit par le GCF que vous avez trouvé précédemment. Ce nombre sera votre plus petit dénominateur commun (LCD). - Exemple: 96/4 = 24
-
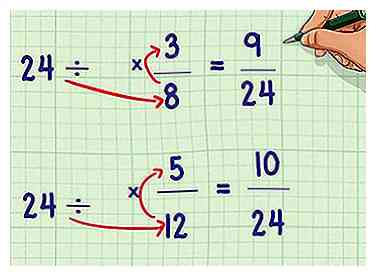 5 Divisez l'écran LCD par le dénominateur d'origine. Pour déterminer le multiple nécessaire pour que les dénominateurs soient égaux, divisez l'écran LCD que vous avez déterminé par le dénominateur d'origine. Multipliez le numérateur et le dénominateur de chaque fraction par ce nombre. Les dénominateurs devraient maintenant être tous deux égaux à l'écran LCD.
5 Divisez l'écran LCD par le dénominateur d'origine. Pour déterminer le multiple nécessaire pour que les dénominateurs soient égaux, divisez l'écran LCD que vous avez déterminé par le dénominateur d'origine. Multipliez le numérateur et le dénominateur de chaque fraction par ce nombre. Les dénominateurs devraient maintenant être tous deux égaux à l'écran LCD. - Exemple: 24/8 = 3; 24/12 = 2
- (3/3) * (3/8) = 9/24; (2/2) * (5/12) = 10/24
- 9/24 + 10/24
-
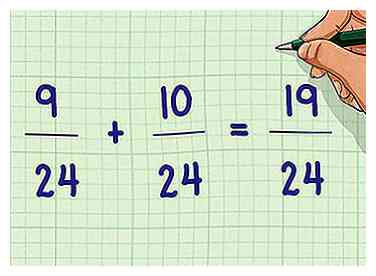 6 Résoudre l'équation réécrite. Avec l'écran LCD trouvé, vous devriez pouvoir ajouter et soustraire les fractions de l'équation sans difficulté supplémentaire. N'oubliez pas de simplifier la fraction à la fin, si possible.
6 Résoudre l'équation réécrite. Avec l'écran LCD trouvé, vous devriez pouvoir ajouter et soustraire les fractions de l'équation sans difficulté supplémentaire. N'oubliez pas de simplifier la fraction à la fin, si possible. - Exemple: 9/24 + 10/24 = 19/24
Méthode trois sur quatre:
Prise en compte de chaque dénominateur dans les prix [5]
-
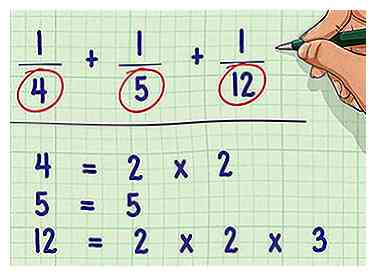 1 Divisez chaque dénominateur en nombres premiers. Comptez chaque chiffre du dénominateur en une série de nombres premiers qui se multiplient pour former ce nombre. Les nombres premiers sont des nombres qui ne peuvent être divisés par aucun autre nombre. [6]
1 Divisez chaque dénominateur en nombres premiers. Comptez chaque chiffre du dénominateur en une série de nombres premiers qui se multiplient pour former ce nombre. Les nombres premiers sont des nombres qui ne peuvent être divisés par aucun autre nombre. [6] - Exemple: 1/4 + 1/5 + 1/12
- Factorisation de 4: 2 * 2
- Factorisation de 5: 5
- Factorisation de 12: 2 * 2 * 3
-
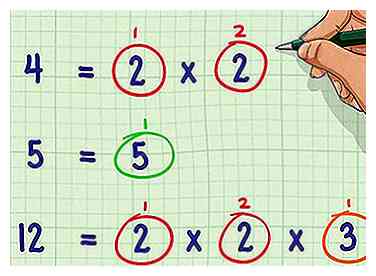 2 Comptez le nombre de fois que chaque nombre premier apparaît dans chaque factorisation. Relevez le nombre de fois que chaque nombre premier apparaît dans la factorisation de chaque chiffre du dénominateur.
2 Comptez le nombre de fois que chaque nombre premier apparaît dans chaque factorisation. Relevez le nombre de fois que chaque nombre premier apparaît dans la factorisation de chaque chiffre du dénominateur. - Exemple: il y a deux 2's en 4; zéro 2's en 5; deux 2's dans 12
- Il y a zéro 3's en 4 et 5; un 3 dans 12
- Il y a zéro 5's en 4 et 12; un 5 dans 5
-
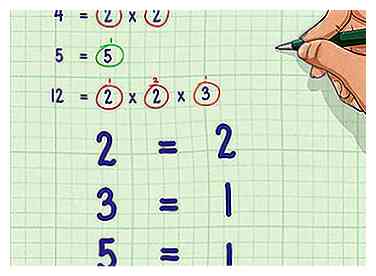 3 Prenez le plus grand nombre pour chaque prime. Identifiez le plus grand nombre de fois que vous avez utilisé chaque nombre premier pour l'un des dénominateurs et notez ce nombre.
3 Prenez le plus grand nombre pour chaque prime. Identifiez le plus grand nombre de fois que vous avez utilisé chaque nombre premier pour l'un des dénominateurs et notez ce nombre. - Exemple: le plus grand nombre de 2 est deux; le plus grand des 3 est une; le plus grand des 5 est une
-
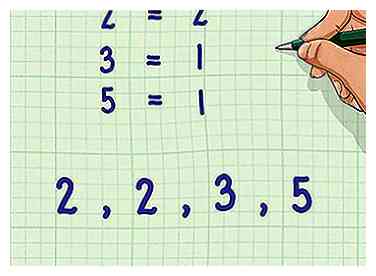 4 Ecrivez ce nombre premier autant de fois que vous avez compté à l'étape précédente. Ne pas écrire le nombre de fois que chaque nombre premier est apparu dans tous les dénominateurs d'origine. N'écrivez que le plus grand nombre, tel que déterminé à l'étape précédente.
4 Ecrivez ce nombre premier autant de fois que vous avez compté à l'étape précédente. Ne pas écrire le nombre de fois que chaque nombre premier est apparu dans tous les dénominateurs d'origine. N'écrivez que le plus grand nombre, tel que déterminé à l'étape précédente. - Exemple: 2, 2, 3, 5
-
 5 Multipliez tous les nombres premiers écrits de cette manière. Multipliez les nombres premiers tels qu'ils apparaissaient à l'étape précédente. Le produit de ces nombres est égal au LCD pour l'équation d'origine.
5 Multipliez tous les nombres premiers écrits de cette manière. Multipliez les nombres premiers tels qu'ils apparaissaient à l'étape précédente. Le produit de ces nombres est égal au LCD pour l'équation d'origine. - Exemple: 2 * 2 * 3 * 5 = 60
- LCD = 60
-
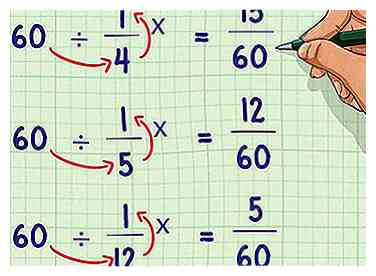 6 Divisez l'écran LCD par le dénominateur d'origine. Pour déterminer le multiple nécessaire pour que les dénominateurs soient égaux, divisez l'écran LCD que vous avez déterminé par le dénominateur d'origine. Multipliez le numérateur et le dénominateur de chaque fraction par ce nombre. Les dénominateurs devraient maintenant être tous deux égaux à l'écran LCD.
6 Divisez l'écran LCD par le dénominateur d'origine. Pour déterminer le multiple nécessaire pour que les dénominateurs soient égaux, divisez l'écran LCD que vous avez déterminé par le dénominateur d'origine. Multipliez le numérateur et le dénominateur de chaque fraction par ce nombre. Les dénominateurs devraient maintenant être tous deux égaux à l'écran LCD. - Exemple: 60/4 = 15; 60/5 = 12; 60/12 = 5
- 15 * (1/4) = 15/60; 12 * (1/5) = 12/60; 5 * (1/12) = 5/60
- 15/60 + 12/60 + 5/60
-
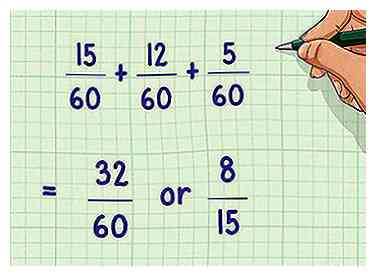 7 Résoudre l'équation réécrite. Avec l'écran LCD trouvé, vous devriez pouvoir ajouter et soustraire les fractions comme d'habitude. N'oubliez pas de simplifier la fraction à la fin, si possible.
7 Résoudre l'équation réécrite. Avec l'écran LCD trouvé, vous devriez pouvoir ajouter et soustraire les fractions comme d'habitude. N'oubliez pas de simplifier la fraction à la fin, si possible. - Exemple: 15/60 + 12/60 + 5/60 = 32/60 = 8/15
Méthode quatre sur quatre:
Travailler avec des nombres entiers et des nombres mixtes [7]
-
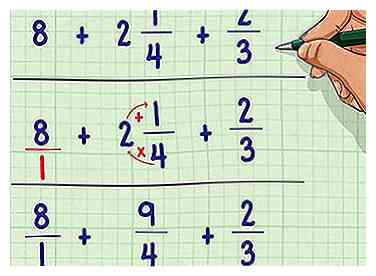 1 Convertir chaque nombre entier et mixte en une fraction impropre. Convertissez des nombres mélangés en fractions impropres en multipliant le nombre entier par le dénominateur et en ajoutant le numérateur au produit. Convertir des nombres entiers en fractions impropres en plaçant le nombre entier sur un dénominateur de «1».
1 Convertir chaque nombre entier et mixte en une fraction impropre. Convertissez des nombres mélangés en fractions impropres en multipliant le nombre entier par le dénominateur et en ajoutant le numérateur au produit. Convertir des nombres entiers en fractions impropres en plaçant le nombre entier sur un dénominateur de «1». - Exemple: 8 + 2 1/4 + 2/3
- 8 = 8/1
- 2 1/4; 2 * 4 + 1 = 8 + 1 = 9; 9/4
- Équation réécrite: 8/1 + 9/4 + 2/3
-
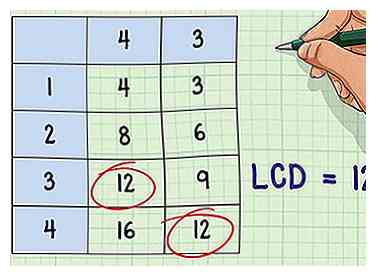 2 Trouvez le plus petit dénominateur commun. Implémentez l'une des méthodes utilisées pour trouver l'écran LCD des fractions communes, comme expliqué dans les sections précédentes. Notez que pour cet exemple, nous utiliserons la méthode des listes multiples, dans laquelle une liste de multiples est créée pour chaque dénominateur et l’écran LCD est identifié à partir de ces listes.
2 Trouvez le plus petit dénominateur commun. Implémentez l'une des méthodes utilisées pour trouver l'écran LCD des fractions communes, comme expliqué dans les sections précédentes. Notez que pour cet exemple, nous utiliserons la méthode des listes multiples, dans laquelle une liste de multiples est créée pour chaque dénominateur et l’écran LCD est identifié à partir de ces listes. - Notez que vous n'avez pas besoin de créer une liste de multiples pour 1 depuis n'importe quel nombre multiplié par 1 égale elle-même; en d'autres termes, chaque nombre est un multiple de 1.
- Exemple: 4 * 1 = 4; 4 * 2 = 8; 4 * 3 = 12; 4 * 4 = 16; etc.
- 3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 * 4 = 12; etc.
- L'écran LCD = 12
-
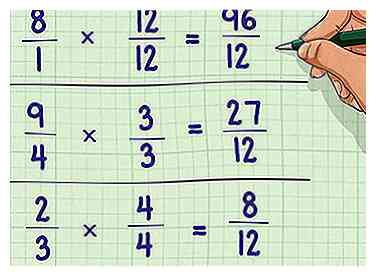 3 Réécrivez l'équation originale. Au lieu de multiplier le dénominateur seul, vous devez multiplier la fraction entière par le chiffre requis pour changer le dénominateur d'origine dans l'écran LCD.
3 Réécrivez l'équation originale. Au lieu de multiplier le dénominateur seul, vous devez multiplier la fraction entière par le chiffre requis pour changer le dénominateur d'origine dans l'écran LCD. - Exemple: (12/12) * (8/1) = 96/12; (3/3) * (9/4) = 27/12; (4/4) * (2/3) = 8/12
- 96/12 + 27/12 + 8/12
-
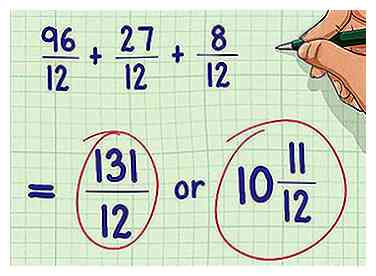 4 Résous l'équation. L'écran LCD étant déterminé et l'équation d'origine modifiée pour refléter l'écran LCD, vous devriez pouvoir ajouter et soustraire sans difficulté. N'oubliez pas de simplifier la fraction à la fin, si possible.
4 Résous l'équation. L'écran LCD étant déterminé et l'équation d'origine modifiée pour refléter l'écran LCD, vous devriez pouvoir ajouter et soustraire sans difficulté. N'oubliez pas de simplifier la fraction à la fin, si possible. - Exemple: 96/12 + 27/12 + 8/12 = 131/12 = 10 11/12
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Énumérez les multiples de chaque dénominateur. Faites une liste de plusieurs multiples pour chaque dénominateur dans l'équation. Chaque liste doit être composée du nombre de dénominateurs multiplié par 1, 2, 3, 4, etc.
1 Énumérez les multiples de chaque dénominateur. Faites une liste de plusieurs multiples pour chaque dénominateur dans l'équation. Chaque liste doit être composée du nombre de dénominateurs multiplié par 1, 2, 3, 4, etc.  2 Identifier le plus petit multiple commun. Parcourez chaque liste et marquez les multiples qui sont partagés par tous les dénominateurs d'origine. Après avoir identifié les multiples communs, identifiez le plus petit dénominateur.
2 Identifier le plus petit multiple commun. Parcourez chaque liste et marquez les multiples qui sont partagés par tous les dénominateurs d'origine. Après avoir identifié les multiples communs, identifiez le plus petit dénominateur.  3 Réécrivez l'équation originale. Afin de changer chaque fraction de l'équation pour qu'elle reste fidèle à l'équation d'origine, vous devrez multiplier chaque numérateur (le haut de la fraction) et le dénominateur par le même facteur que celui utilisé pour multiplier le dénominateur correspondant lorsque vous atteignez le LCD.
3 Réécrivez l'équation originale. Afin de changer chaque fraction de l'équation pour qu'elle reste fidèle à l'équation d'origine, vous devrez multiplier chaque numérateur (le haut de la fraction) et le dénominateur par le même facteur que celui utilisé pour multiplier le dénominateur correspondant lorsque vous atteignez le LCD. 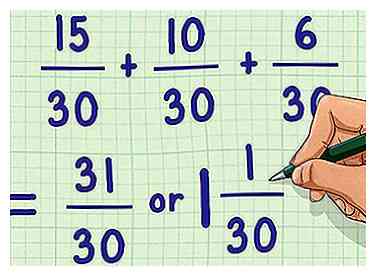 4 Résoudre le problème réécrit. Après avoir trouvé l'écran LCD et modifié les fractions en conséquence, vous devriez pouvoir résoudre le problème sans difficulté supplémentaire. N'oubliez pas de simplifier la fraction à la fin.
4 Résoudre le problème réécrit. Après avoir trouvé l'écran LCD et modifié les fractions en conséquence, vous devriez pouvoir résoudre le problème sans difficulté supplémentaire. N'oubliez pas de simplifier la fraction à la fin.  1 Énumérez tous les facteurs de chaque dénominateur. Les facteurs d'un nombre sont tous les nombres entiers qui peuvent être divisés en un seul nombre.[4] Le nombre 6 a quatre facteurs: 6, 3, 2 et 1. Chaque nombre a un facteur de 1 car chaque nombre peut être multiplié par un.
1 Énumérez tous les facteurs de chaque dénominateur. Les facteurs d'un nombre sont tous les nombres entiers qui peuvent être divisés en un seul nombre.[4] Le nombre 6 a quatre facteurs: 6, 3, 2 et 1. Chaque nombre a un facteur de 1 car chaque nombre peut être multiplié par un.  2 Identifier le plus grand facteur commun entre les deux dénominateurs. Une fois que vous avez énuméré les facteurs de chaque dénominateur, encerclez tous les facteurs communs. Le plus grand des facteurs communs est le plus grand facteur commun (GCF) qui sera utilisé pour continuer à résoudre le problème.
2 Identifier le plus grand facteur commun entre les deux dénominateurs. Une fois que vous avez énuméré les facteurs de chaque dénominateur, encerclez tous les facteurs communs. Le plus grand des facteurs communs est le plus grand facteur commun (GCF) qui sera utilisé pour continuer à résoudre le problème. 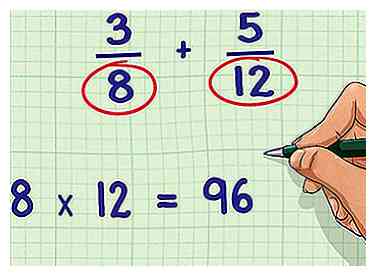 3 Multipliez les dénominateurs ensemble. Afin d'utiliser le plus grand facteur commun pour résoudre le problème, vous devez d'abord multiplier les deux dénominateurs ensemble.
3 Multipliez les dénominateurs ensemble. Afin d'utiliser le plus grand facteur commun pour résoudre le problème, vous devez d'abord multiplier les deux dénominateurs ensemble. 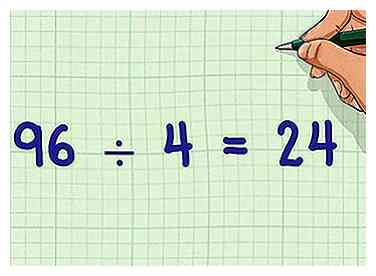 4 Diviser ce produit par le GCF. Après avoir trouvé le produit des deux dénominateurs, divisez ce produit par le GCF que vous avez trouvé précédemment. Ce nombre sera votre plus petit dénominateur commun (LCD).
4 Diviser ce produit par le GCF. Après avoir trouvé le produit des deux dénominateurs, divisez ce produit par le GCF que vous avez trouvé précédemment. Ce nombre sera votre plus petit dénominateur commun (LCD).  5 Divisez l'écran LCD par le dénominateur d'origine. Pour déterminer le multiple nécessaire pour que les dénominateurs soient égaux, divisez l'écran LCD que vous avez déterminé par le dénominateur d'origine. Multipliez le numérateur et le dénominateur de chaque fraction par ce nombre. Les dénominateurs devraient maintenant être tous deux égaux à l'écran LCD.
5 Divisez l'écran LCD par le dénominateur d'origine. Pour déterminer le multiple nécessaire pour que les dénominateurs soient égaux, divisez l'écran LCD que vous avez déterminé par le dénominateur d'origine. Multipliez le numérateur et le dénominateur de chaque fraction par ce nombre. Les dénominateurs devraient maintenant être tous deux égaux à l'écran LCD. 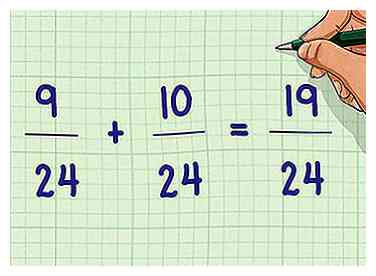 6 Résoudre l'équation réécrite. Avec l'écran LCD trouvé, vous devriez pouvoir ajouter et soustraire les fractions de l'équation sans difficulté supplémentaire. N'oubliez pas de simplifier la fraction à la fin, si possible.
6 Résoudre l'équation réécrite. Avec l'écran LCD trouvé, vous devriez pouvoir ajouter et soustraire les fractions de l'équation sans difficulté supplémentaire. N'oubliez pas de simplifier la fraction à la fin, si possible.  1 Divisez chaque dénominateur en nombres premiers. Comptez chaque chiffre du dénominateur en une série de nombres premiers qui se multiplient pour former ce nombre. Les nombres premiers sont des nombres qui ne peuvent être divisés par aucun autre nombre. [6]
1 Divisez chaque dénominateur en nombres premiers. Comptez chaque chiffre du dénominateur en une série de nombres premiers qui se multiplient pour former ce nombre. Les nombres premiers sont des nombres qui ne peuvent être divisés par aucun autre nombre. [6]  2 Comptez le nombre de fois que chaque nombre premier apparaît dans chaque factorisation. Relevez le nombre de fois que chaque nombre premier apparaît dans la factorisation de chaque chiffre du dénominateur.
2 Comptez le nombre de fois que chaque nombre premier apparaît dans chaque factorisation. Relevez le nombre de fois que chaque nombre premier apparaît dans la factorisation de chaque chiffre du dénominateur. 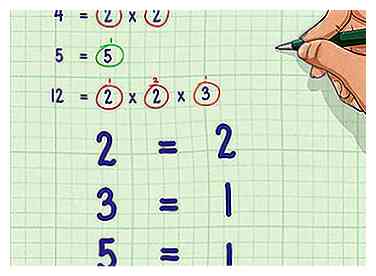 3 Prenez le plus grand nombre pour chaque prime. Identifiez le plus grand nombre de fois que vous avez utilisé chaque nombre premier pour l'un des dénominateurs et notez ce nombre.
3 Prenez le plus grand nombre pour chaque prime. Identifiez le plus grand nombre de fois que vous avez utilisé chaque nombre premier pour l'un des dénominateurs et notez ce nombre.  4 Ecrivez ce nombre premier autant de fois que vous avez compté à l'étape précédente. Ne pas écrire le nombre de fois que chaque nombre premier est apparu dans tous les dénominateurs d'origine. N'écrivez que le plus grand nombre, tel que déterminé à l'étape précédente.
4 Ecrivez ce nombre premier autant de fois que vous avez compté à l'étape précédente. Ne pas écrire le nombre de fois que chaque nombre premier est apparu dans tous les dénominateurs d'origine. N'écrivez que le plus grand nombre, tel que déterminé à l'étape précédente.  5 Multipliez tous les nombres premiers écrits de cette manière. Multipliez les nombres premiers tels qu'ils apparaissaient à l'étape précédente. Le produit de ces nombres est égal au LCD pour l'équation d'origine.
5 Multipliez tous les nombres premiers écrits de cette manière. Multipliez les nombres premiers tels qu'ils apparaissaient à l'étape précédente. Le produit de ces nombres est égal au LCD pour l'équation d'origine.  6 Divisez l'écran LCD par le dénominateur d'origine. Pour déterminer le multiple nécessaire pour que les dénominateurs soient égaux, divisez l'écran LCD que vous avez déterminé par le dénominateur d'origine. Multipliez le numérateur et le dénominateur de chaque fraction par ce nombre. Les dénominateurs devraient maintenant être tous deux égaux à l'écran LCD.
6 Divisez l'écran LCD par le dénominateur d'origine. Pour déterminer le multiple nécessaire pour que les dénominateurs soient égaux, divisez l'écran LCD que vous avez déterminé par le dénominateur d'origine. Multipliez le numérateur et le dénominateur de chaque fraction par ce nombre. Les dénominateurs devraient maintenant être tous deux égaux à l'écran LCD.  7 Résoudre l'équation réécrite. Avec l'écran LCD trouvé, vous devriez pouvoir ajouter et soustraire les fractions comme d'habitude. N'oubliez pas de simplifier la fraction à la fin, si possible.
7 Résoudre l'équation réécrite. Avec l'écran LCD trouvé, vous devriez pouvoir ajouter et soustraire les fractions comme d'habitude. N'oubliez pas de simplifier la fraction à la fin, si possible.  1 Convertir chaque nombre entier et mixte en une fraction impropre. Convertissez des nombres mélangés en fractions impropres en multipliant le nombre entier par le dénominateur et en ajoutant le numérateur au produit. Convertir des nombres entiers en fractions impropres en plaçant le nombre entier sur un dénominateur de «1».
1 Convertir chaque nombre entier et mixte en une fraction impropre. Convertissez des nombres mélangés en fractions impropres en multipliant le nombre entier par le dénominateur et en ajoutant le numérateur au produit. Convertir des nombres entiers en fractions impropres en plaçant le nombre entier sur un dénominateur de «1».  2 Trouvez le plus petit dénominateur commun. Implémentez l'une des méthodes utilisées pour trouver l'écran LCD des fractions communes, comme expliqué dans les sections précédentes. Notez que pour cet exemple, nous utiliserons la méthode des listes multiples, dans laquelle une liste de multiples est créée pour chaque dénominateur et l’écran LCD est identifié à partir de ces listes.
2 Trouvez le plus petit dénominateur commun. Implémentez l'une des méthodes utilisées pour trouver l'écran LCD des fractions communes, comme expliqué dans les sections précédentes. Notez que pour cet exemple, nous utiliserons la méthode des listes multiples, dans laquelle une liste de multiples est créée pour chaque dénominateur et l’écran LCD est identifié à partir de ces listes.  3 Réécrivez l'équation originale. Au lieu de multiplier le dénominateur seul, vous devez multiplier la fraction entière par le chiffre requis pour changer le dénominateur d'origine dans l'écran LCD.
3 Réécrivez l'équation originale. Au lieu de multiplier le dénominateur seul, vous devez multiplier la fraction entière par le chiffre requis pour changer le dénominateur d'origine dans l'écran LCD.  4 Résous l'équation. L'écran LCD étant déterminé et l'équation d'origine modifiée pour refléter l'écran LCD, vous devriez pouvoir ajouter et soustraire sans difficulté. N'oubliez pas de simplifier la fraction à la fin, si possible.
4 Résous l'équation. L'écran LCD étant déterminé et l'équation d'origine modifiée pour refléter l'écran LCD, vous devriez pouvoir ajouter et soustraire sans difficulté. N'oubliez pas de simplifier la fraction à la fin, si possible.