Deux fractions sont équivalentes si elles ont la même valeur. Savoir comment convertir une fraction en une fraction équivalente est une compétence mathématique essentielle pour tout, de l'algèbre de base au calcul avancé. Cet article couvrira plusieurs manières de calculer des fractions équivalentes de la multiplication de base et de la division à des méthodes plus complexes pour résoudre des équations de fractions équivalentes.
Méthode One of Five:
Formant des fractions équivalentes
-
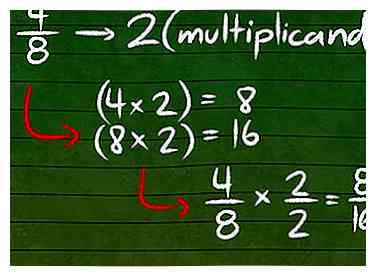 1 Multipliez le numérateur et le dénominateur par le même nombre. Deux fractions différentes mais équivalentes ont, par définition, des numérateurs et des dénominateurs multiples les uns des autres. En d'autres termes, multiplier le numérateur et le dénominateur d'une fraction par le même nombre produira une fraction équivalente. Bien que les nombres dans la nouvelle fraction soient différents, les fractions auront la même valeur.
1 Multipliez le numérateur et le dénominateur par le même nombre. Deux fractions différentes mais équivalentes ont, par définition, des numérateurs et des dénominateurs multiples les uns des autres. En d'autres termes, multiplier le numérateur et le dénominateur d'une fraction par le même nombre produira une fraction équivalente. Bien que les nombres dans la nouvelle fraction soient différents, les fractions auront la même valeur. - Par exemple, si nous prenons la fraction 4/8 et multiplions le numérateur et le dénominateur par 2, nous obtenons (4 × 2) / (8 × 2) = 8/16. Ces deux fractions sont équivalentes.
- (4 × 2) / (8 × 2) est sensiblement le même que 4/8 × 2/2
- Notez que 2/2 est égal à 1 lorsque vous effectuez la division. Ainsi, il est facile de voir pourquoi 4/8 et 8/16 sont équivalents car en multipliant 4/8 × (2/2) = 4/8 encore. De la même manière, il est juste de dire que 4/8 = 8/16.
- Toute fraction donnée a un nombre infini de fractions équivalentes. Vous pouvez multiplier le numérateur et le dénominateur par tout nombre entier, quelle que soit sa taille pour obtenir une fraction équivalente.
-
 2 Diviser le numérateur et le dénominateur par le même nombre. Comme la multiplication, la division peut également être utilisée pour trouver une nouvelle fraction équivalente à votre fraction de départ. Divisez simplement le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Il y a une mise en garde à ce processus - la fraction résultante doit avoir des nombres entiers à la fois au numérateur et au dénominateur pour être valide.
2 Diviser le numérateur et le dénominateur par le même nombre. Comme la multiplication, la division peut également être utilisée pour trouver une nouvelle fraction équivalente à votre fraction de départ. Divisez simplement le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Il y a une mise en garde à ce processus - la fraction résultante doit avoir des nombres entiers à la fois au numérateur et au dénominateur pour être valide. - Par exemple, regardons à nouveau 4/8. Si, au lieu de multiplier, on divise le numérateur et le dénominateur par 2, on obtient (4 ÷ 2) / (8 ÷ 2) = 2/4. 2 et 4 sont tous deux des nombres entiers, donc cette fraction équivalente est valide.
Méthode deux sur cinq:
Utilisation de la multiplication de base pour déterminer l'équivalence
-
 1 Trouvez le nombre par lequel le plus petit dénominateur doit être multiplié pour obtenir le plus grand dénominateur. De nombreux problèmes concernant les fractions impliquent de déterminer si deux fractions sont équivalentes. En calculant ce nombre, vous pouvez commencer à mettre les fractions dans les mêmes termes pour déterminer l’équivalence.
1 Trouvez le nombre par lequel le plus petit dénominateur doit être multiplié pour obtenir le plus grand dénominateur. De nombreux problèmes concernant les fractions impliquent de déterminer si deux fractions sont équivalentes. En calculant ce nombre, vous pouvez commencer à mettre les fractions dans les mêmes termes pour déterminer l’équivalence. - Par exemple, reprenez les fractions 4/8 et 8/16. Le plus petit dénominateur est 8, et il faudrait multiplier ce nombre x2 pour obtenir le plus grand dénominateur, à savoir 16. Par conséquent, le nombre est 2.
- Pour les nombres plus difficiles, vous pouvez simplement diviser le plus grand dénominateur par le plus petit dénominateur. Dans ce cas, 16 divisé par 8, ce qui nous donne encore 2.
- Le nombre peut ne pas toujours être un nombre entier. Par exemple, si les dénominateurs étaient 2 et 7, alors le nombre serait de 3,5.
-
 2 Multipliez le numérateur et le dénominateur de la fraction exprimée en termes plus faibles par le nombre de la première étape. Deux fractions différentes mais équivalentes ont, par définition, numérateurs et dénominateurs qui sont des multiples les uns des autres. En d'autres termes, multiplier le numérateur et le dénominateur d'une fraction par le même nombre produira une fraction équivalente. Bien que les nombres dans cette nouvelle fraction soient différents, les fractions auront la même valeur.[1]
2 Multipliez le numérateur et le dénominateur de la fraction exprimée en termes plus faibles par le nombre de la première étape. Deux fractions différentes mais équivalentes ont, par définition, numérateurs et dénominateurs qui sont des multiples les uns des autres. En d'autres termes, multiplier le numérateur et le dénominateur d'une fraction par le même nombre produira une fraction équivalente. Bien que les nombres dans cette nouvelle fraction soient différents, les fractions auront la même valeur.[1] - Par exemple, si nous prenons la fraction 4/8 de l’étape 1 et que nous multiplions à la fois le numérateur et le dénominateur par notre nombre 2 précédemment déterminé, nous obtenons (4 × 2) / (8 × 2) = 8/16. Prouvant ainsi que ces deux fractions sont équivalentes.
Méthode trois sur cinq:
Utilisation de la division de base pour déterminer l'équivalence
-
 1 Calculer chaque fraction en nombre décimal. Pour les fractions simples sans variables, vous pouvez simplement exprimer chaque fraction comme un nombre décimal pour déterminer l'équivalence. Puisque chaque fraction est en fait un problème de division au départ, c'est la manière la plus simple de déterminer l'équivalence.
1 Calculer chaque fraction en nombre décimal. Pour les fractions simples sans variables, vous pouvez simplement exprimer chaque fraction comme un nombre décimal pour déterminer l'équivalence. Puisque chaque fraction est en fait un problème de division au départ, c'est la manière la plus simple de déterminer l'équivalence. - Par exemple, prenez notre précédent 4/8. La fraction 4/8 équivaut à dire 4 divisé par 8, 4/8 = 0,5. Vous pouvez également résoudre l'autre exemple, qui est 8/16 = 0.5. Indépendamment des termes d'une fraction, ils sont équivalents si les deux nombres sont exactement les mêmes lorsqu'ils sont exprimés en décimal.
- Rappelez-vous que l'expression décimale peut faire plusieurs chiffres avant que le manque d'équivalence ne devienne apparent. Comme exemple de base, 1/3 = 0,333 en répétant alors que 3/10 = 0,3. En utilisant plus d'un chiffre, on voit que ces deux fractions ne sont pas équivalentes.
-
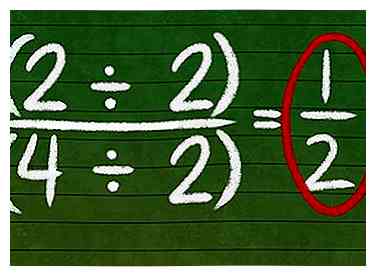 2 Diviser le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Pour les fractions plus complexes, la méthode de division nécessite des étapes supplémentaires. Comme avec la méthode de multiplication, vous pouvez diviser le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Il y a une réserve à ce processus. La fraction résultante doit avoir des nombres entiers à la fois au numérateur et au dénominateur pour être valide.
2 Diviser le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Pour les fractions plus complexes, la méthode de division nécessite des étapes supplémentaires. Comme avec la méthode de multiplication, vous pouvez diviser le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Il y a une réserve à ce processus. La fraction résultante doit avoir des nombres entiers à la fois au numérateur et au dénominateur pour être valide. - Par exemple, regardons à nouveau 4/8. Si, au lieu de multiplier, nous diviser à la fois le numérateur et le dénominateur par 2, nous obtenons (4 ÷ 2) / (8 ÷ 2) = 2/4. 2 et 4 sont tous deux des nombres entiers, donc cette fraction équivalente est valide.
-
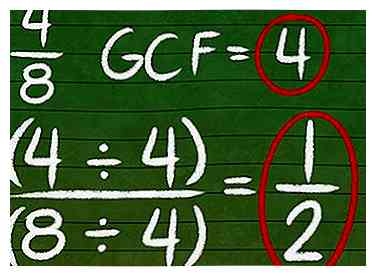 3 Réduire les fractions à leurs conditions les plus basses. La plupart des fractions doivent généralement être exprimées dans leurs termes les plus bas et vous pouvez convertir les fractions en leurs termes les plus simples en divisant par leur plus grand facteur commun (GCF). Cette étape opère par la même logique d’expression des fractions équivalentes en les convertissant pour avoir le même dénominateur, mais cette méthode cherche à réduire chaque fraction à ses termes exprimables les plus bas.
3 Réduire les fractions à leurs conditions les plus basses. La plupart des fractions doivent généralement être exprimées dans leurs termes les plus bas et vous pouvez convertir les fractions en leurs termes les plus simples en divisant par leur plus grand facteur commun (GCF). Cette étape opère par la même logique d’expression des fractions équivalentes en les convertissant pour avoir le même dénominateur, mais cette méthode cherche à réduire chaque fraction à ses termes exprimables les plus bas. - Lorsqu'une fraction est dans ses termes les plus simples, son numérateur et son dénominateur sont tous deux aussi petits que possible. Aucun des deux ne peut être divisé par un nombre entier pour obtenir quelque chose de plus petit. Pour convertir une fraction qui est ne pas en termes les plus simples à une forme équivalente est, nous divisons le numérateur et le dénominateur par leur le plus grand facteur commun.
- Le plus grand facteur commun (GCF) du numérateur et du dénominateur est le plus grand nombre qui se divise en deux pour donner un résultat en nombre entier. Donc, dans notre exemple 4/8, depuis 4 est le plus grand nombre qui se divise uniformément dans 4 et 8, nous diviserions le numérateur et le dénominateur de notre fraction par 4 pour l’obtenir en termes les plus simples. (4 ÷ 4) / (8 ÷ 4) = 1/2. Pour notre autre exemple de 8/16, le GCF est 8, ce qui donne également 1/2 comme expression la plus simple de la fraction.
Méthode quatre sur cinq:
Utiliser la multiplication croisée pour résoudre une variable
-
 1 Définissez les deux fractions égales. Nous utilisons la multiplication croisée pour les problèmes mathématiques où nous savons que les fractions sont équivalentes, mais l'un des nombres a été remplacé par une variable (généralement x) pour laquelle nous devons résoudre. Dans de tels cas, nous savons que ces fractions sont équivalentes car ce sont les seuls termes sur les côtés opposés d’un signe égal, mais il n’est souvent pas évident de savoir comment résoudre la variable. Heureusement, avec la multiplication croisée, il est facile de résoudre ces types de problèmes.[2]
1 Définissez les deux fractions égales. Nous utilisons la multiplication croisée pour les problèmes mathématiques où nous savons que les fractions sont équivalentes, mais l'un des nombres a été remplacé par une variable (généralement x) pour laquelle nous devons résoudre. Dans de tels cas, nous savons que ces fractions sont équivalentes car ce sont les seuls termes sur les côtés opposés d’un signe égal, mais il n’est souvent pas évident de savoir comment résoudre la variable. Heureusement, avec la multiplication croisée, il est facile de résoudre ces types de problèmes.[2] -
 2 Prenez les deux fractions équivalentes et multipliez-les sur le signe égal en "X". En d'autres termes, vous multipliez le numérateur d'une fraction par le dénominateur de l'autre et vice versa, puis vous mettez ces deux réponses égales et vous résolvez.[3]
2 Prenez les deux fractions équivalentes et multipliez-les sur le signe égal en "X". En d'autres termes, vous multipliez le numérateur d'une fraction par le dénominateur de l'autre et vice versa, puis vous mettez ces deux réponses égales et vous résolvez.[3] - Prenez nos deux exemples de 4/8 et 8/16. Ces deux ne contiennent pas de variable, mais nous pouvons prouver le concept puisque nous savons déjà qu'ils sont équivalents. En multipliant en croix, on obtient 4 x 16 = 8 x 8, ou 64 = 64, ce qui est évidemment vrai. Si les deux nombres ne sont pas les mêmes, les fractions ne sont pas équivalentes.
-
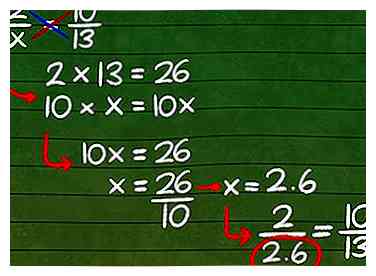 3 Introduire une variable. Étant donné que la multiplication croisée est le moyen le plus simple de déterminer des fractions équivalentes lorsque vous devez résoudre une variable, ajoutons une variable.
3 Introduire une variable. Étant donné que la multiplication croisée est le moyen le plus simple de déterminer des fractions équivalentes lorsque vous devez résoudre une variable, ajoutons une variable. - Par exemple, considérons l'équation 2 / x = 10/13. Pour se multiplier, on multiplie 2 par 13 et 10 par x, puis on établit des réponses égales:
- 2 × 13 = 26
- 10 × x = 10x
- 10x = 26. À partir de là, obtenir une réponse à notre variable relève de la simple algèbre. x = 26/10 = 2.6, en faisant les fractions équivalentes initiales 2 / 2,6 = 10/13.
- Par exemple, considérons l'équation 2 / x = 10/13. Pour se multiplier, on multiplie 2 par 13 et 10 par x, puis on établit des réponses égales:
-
 4 Utilisez la multiplication croisée pour les équations avec plusieurs variables ou expressions de variable. L'une des meilleures choses à propos de la multiplication croisée est qu'elle fonctionne essentiellement de la même manière, que vous traitiez de deux fractions simples (comme ci-dessus) ou de fractions plus complexes. Par exemple, si les deux fractions contiennent des variables, il vous suffit d'éliminer ces variables à la fin du processus de résolution. De même, si les numérateurs ou les dénominateurs de vos fractions contiennent des expressions variables (telles que x + 1), il suffit de "multiplier" en utilisant la propriété distributive et de résoudre comme vous le feriez normalement.[4]
4 Utilisez la multiplication croisée pour les équations avec plusieurs variables ou expressions de variable. L'une des meilleures choses à propos de la multiplication croisée est qu'elle fonctionne essentiellement de la même manière, que vous traitiez de deux fractions simples (comme ci-dessus) ou de fractions plus complexes. Par exemple, si les deux fractions contiennent des variables, il vous suffit d'éliminer ces variables à la fin du processus de résolution. De même, si les numérateurs ou les dénominateurs de vos fractions contiennent des expressions variables (telles que x + 1), il suffit de "multiplier" en utilisant la propriété distributive et de résoudre comme vous le feriez normalement.[4] - Considérons par exemple l’équation ((x + 3) / 2) = ((x + 1) / 4). Dans ce cas, comme ci-dessus, nous allons résoudre en multipliant par:
- (x + 3) × 4 = 4x + 12
- (x + 1) × 2 = 2x + 2
- 2x + 2 = 4x + 12, alors on peut simplifier l'équation en soustrayant 2x des deux côtés
- 2 = 2x + 12, alors nous devrions isoler la variable en soustrayant 12 des deux côtés
- -10 = 2x, et diviser par 2 pour résoudre x
- -5 = x
- Considérons par exemple l’équation ((x + 3) / 2) = ((x + 1) / 4). Dans ce cas, comme ci-dessus, nous allons résoudre en multipliant par:
Méthode cinq sur cinq:
Utiliser la formule quadratique pour résoudre les variables
-
 1 Croix multiplier les deux fractions. Pour les problèmes d'équivalence nécessitant la formule quadratique, nous commençons toujours par utiliser la multiplication croisée. Cependant, toute multiplication croisée impliquant la multiplication de termes variables par d'autres termes variables est susceptible d'entraîner une expression difficile à résoudre par l'algèbre. Dans de tels cas, vous devrez peut-être utiliser des techniques telles que l'affacturage et / ou la formule quadratique.[5]
1 Croix multiplier les deux fractions. Pour les problèmes d'équivalence nécessitant la formule quadratique, nous commençons toujours par utiliser la multiplication croisée. Cependant, toute multiplication croisée impliquant la multiplication de termes variables par d'autres termes variables est susceptible d'entraîner une expression difficile à résoudre par l'algèbre. Dans de tels cas, vous devrez peut-être utiliser des techniques telles que l'affacturage et / ou la formule quadratique.[5] - Par exemple, regardons l'équation ((x +1) / 3) = (4 / (2x - 2)). Tout d'abord, croisons-nous:
- (x + 1) × (2x - 2) = 2x2 + 2x -2x - 2 = 2x2 - 2
- 4 × 3 = 12
- 2x2 - 2 = 12.
- Par exemple, regardons l'équation ((x +1) / 3) = (4 / (2x - 2)). Tout d'abord, croisons-nous:
-
 2 Exprimez l'équation comme une équation quadratique. À ce stade, nous voulons exprimer cette équation sous forme quadratique (ax2 + bx + c = 0), ce que nous faisons en réglant l’équation à zéro. Dans ce cas, nous soustrayons 12 des deux côtés pour obtenir 2x2 - 14 = 0.
2 Exprimez l'équation comme une équation quadratique. À ce stade, nous voulons exprimer cette équation sous forme quadratique (ax2 + bx + c = 0), ce que nous faisons en réglant l’équation à zéro. Dans ce cas, nous soustrayons 12 des deux côtés pour obtenir 2x2 - 14 = 0. - Certaines valeurs peuvent être égales à 0. Bien que 2x2 - 14 = 0 est la forme la plus simple de notre équation, l’équation quadratique vraie est 2x2 + 0x + (-14) = 0. Cela va probablement aider à reproduire tôt la forme de l'équation quadratique, même si certaines valeurs sont égales à 0.
-
 3 Résoudre en branchant les nombres de votre équation quadratique dans la formule quadratique. La formule quadratique (x = (-b +/- √ (b2 - 4ac)) / 2a) nous aidera à résoudre notre valeur x à ce stade.[6] Ne soyez pas intimidé par la longueur de la formule. Vous prenez simplement les valeurs de votre équation quadratique à l'étape deux et les connectez aux endroits appropriés avant de les résoudre.
3 Résoudre en branchant les nombres de votre équation quadratique dans la formule quadratique. La formule quadratique (x = (-b +/- √ (b2 - 4ac)) / 2a) nous aidera à résoudre notre valeur x à ce stade.[6] Ne soyez pas intimidé par la longueur de la formule. Vous prenez simplement les valeurs de votre équation quadratique à l'étape deux et les connectez aux endroits appropriés avant de les résoudre. - x = (-b +/- √ (b2 - 4ac)) / 2a. Dans notre équation, 2x2 - 14 = 0, a = 2, b = 0 et c = -14.
- x = (-0 +/- √ (02 - 4(2)(-14)))/2(2)
- x = (+/- √ (0 - -112)) / 2 (2)
- x = (+/- √ (112)) / 2 (2)
- x = (+/- 10,58 / 4)
- x = +/- 2.64
-
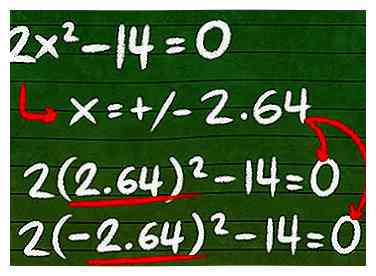 4 Vérifiez votre réponse en branchant la valeur x dans votre équation quadratique. En branchant la valeur calculée de x dans votre équation quadratique de l'étape deux, vous pouvez facilement déterminer si vous avez atteint la bonne réponse.[7] Dans cet exemple, vous branchez à la fois 2,64 et -2,64 dans l’équation quadratique originale.
4 Vérifiez votre réponse en branchant la valeur x dans votre équation quadratique. En branchant la valeur calculée de x dans votre équation quadratique de l'étape deux, vous pouvez facilement déterminer si vous avez atteint la bonne réponse.[7] Dans cet exemple, vous branchez à la fois 2,64 et -2,64 dans l’équation quadratique originale.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
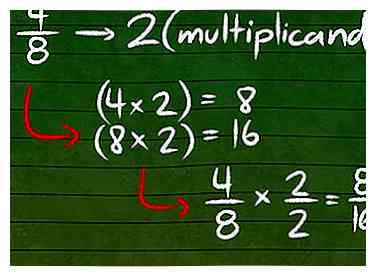 1 Multipliez le numérateur et le dénominateur par le même nombre. Deux fractions différentes mais équivalentes ont, par définition, des numérateurs et des dénominateurs multiples les uns des autres. En d'autres termes, multiplier le numérateur et le dénominateur d'une fraction par le même nombre produira une fraction équivalente. Bien que les nombres dans la nouvelle fraction soient différents, les fractions auront la même valeur.
1 Multipliez le numérateur et le dénominateur par le même nombre. Deux fractions différentes mais équivalentes ont, par définition, des numérateurs et des dénominateurs multiples les uns des autres. En d'autres termes, multiplier le numérateur et le dénominateur d'une fraction par le même nombre produira une fraction équivalente. Bien que les nombres dans la nouvelle fraction soient différents, les fractions auront la même valeur.  2 Diviser le numérateur et le dénominateur par le même nombre. Comme la multiplication, la division peut également être utilisée pour trouver une nouvelle fraction équivalente à votre fraction de départ. Divisez simplement le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Il y a une mise en garde à ce processus - la fraction résultante doit avoir des nombres entiers à la fois au numérateur et au dénominateur pour être valide.
2 Diviser le numérateur et le dénominateur par le même nombre. Comme la multiplication, la division peut également être utilisée pour trouver une nouvelle fraction équivalente à votre fraction de départ. Divisez simplement le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Il y a une mise en garde à ce processus - la fraction résultante doit avoir des nombres entiers à la fois au numérateur et au dénominateur pour être valide.  1 Trouvez le nombre par lequel le plus petit dénominateur doit être multiplié pour obtenir le plus grand dénominateur. De nombreux problèmes concernant les fractions impliquent de déterminer si deux fractions sont équivalentes. En calculant ce nombre, vous pouvez commencer à mettre les fractions dans les mêmes termes pour déterminer l’équivalence.
1 Trouvez le nombre par lequel le plus petit dénominateur doit être multiplié pour obtenir le plus grand dénominateur. De nombreux problèmes concernant les fractions impliquent de déterminer si deux fractions sont équivalentes. En calculant ce nombre, vous pouvez commencer à mettre les fractions dans les mêmes termes pour déterminer l’équivalence.  2 Multipliez le numérateur et le dénominateur de la fraction exprimée en termes plus faibles par le nombre de la première étape. Deux fractions différentes mais équivalentes ont, par définition, numérateurs et dénominateurs qui sont des multiples les uns des autres. En d'autres termes, multiplier le numérateur et le dénominateur d'une fraction par le même nombre produira une fraction équivalente. Bien que les nombres dans cette nouvelle fraction soient différents, les fractions auront la même valeur.[1]
2 Multipliez le numérateur et le dénominateur de la fraction exprimée en termes plus faibles par le nombre de la première étape. Deux fractions différentes mais équivalentes ont, par définition, numérateurs et dénominateurs qui sont des multiples les uns des autres. En d'autres termes, multiplier le numérateur et le dénominateur d'une fraction par le même nombre produira une fraction équivalente. Bien que les nombres dans cette nouvelle fraction soient différents, les fractions auront la même valeur.[1]  1 Calculer chaque fraction en nombre décimal. Pour les fractions simples sans variables, vous pouvez simplement exprimer chaque fraction comme un nombre décimal pour déterminer l'équivalence. Puisque chaque fraction est en fait un problème de division au départ, c'est la manière la plus simple de déterminer l'équivalence.
1 Calculer chaque fraction en nombre décimal. Pour les fractions simples sans variables, vous pouvez simplement exprimer chaque fraction comme un nombre décimal pour déterminer l'équivalence. Puisque chaque fraction est en fait un problème de division au départ, c'est la manière la plus simple de déterminer l'équivalence. 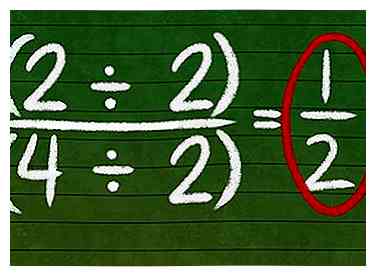 2 Diviser le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Pour les fractions plus complexes, la méthode de division nécessite des étapes supplémentaires. Comme avec la méthode de multiplication, vous pouvez diviser le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Il y a une réserve à ce processus. La fraction résultante doit avoir des nombres entiers à la fois au numérateur et au dénominateur pour être valide.
2 Diviser le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Pour les fractions plus complexes, la méthode de division nécessite des étapes supplémentaires. Comme avec la méthode de multiplication, vous pouvez diviser le numérateur et le dénominateur d'une fraction par le même nombre pour obtenir une fraction équivalente. Il y a une réserve à ce processus. La fraction résultante doit avoir des nombres entiers à la fois au numérateur et au dénominateur pour être valide. 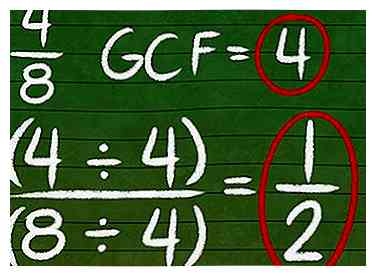 3 Réduire les fractions à leurs conditions les plus basses. La plupart des fractions doivent généralement être exprimées dans leurs termes les plus bas et vous pouvez convertir les fractions en leurs termes les plus simples en divisant par leur plus grand facteur commun (GCF). Cette étape opère par la même logique d’expression des fractions équivalentes en les convertissant pour avoir le même dénominateur, mais cette méthode cherche à réduire chaque fraction à ses termes exprimables les plus bas.
3 Réduire les fractions à leurs conditions les plus basses. La plupart des fractions doivent généralement être exprimées dans leurs termes les plus bas et vous pouvez convertir les fractions en leurs termes les plus simples en divisant par leur plus grand facteur commun (GCF). Cette étape opère par la même logique d’expression des fractions équivalentes en les convertissant pour avoir le même dénominateur, mais cette méthode cherche à réduire chaque fraction à ses termes exprimables les plus bas.  1 Définissez les deux fractions égales. Nous utilisons la multiplication croisée pour les problèmes mathématiques où nous savons que les fractions sont équivalentes, mais l'un des nombres a été remplacé par une variable (généralement x) pour laquelle nous devons résoudre. Dans de tels cas, nous savons que ces fractions sont équivalentes car ce sont les seuls termes sur les côtés opposés d’un signe égal, mais il n’est souvent pas évident de savoir comment résoudre la variable. Heureusement, avec la multiplication croisée, il est facile de résoudre ces types de problèmes.[2]
1 Définissez les deux fractions égales. Nous utilisons la multiplication croisée pour les problèmes mathématiques où nous savons que les fractions sont équivalentes, mais l'un des nombres a été remplacé par une variable (généralement x) pour laquelle nous devons résoudre. Dans de tels cas, nous savons que ces fractions sont équivalentes car ce sont les seuls termes sur les côtés opposés d’un signe égal, mais il n’est souvent pas évident de savoir comment résoudre la variable. Heureusement, avec la multiplication croisée, il est facile de résoudre ces types de problèmes.[2]  2 Prenez les deux fractions équivalentes et multipliez-les sur le signe égal en "X". En d'autres termes, vous multipliez le numérateur d'une fraction par le dénominateur de l'autre et vice versa, puis vous mettez ces deux réponses égales et vous résolvez.[3]
2 Prenez les deux fractions équivalentes et multipliez-les sur le signe égal en "X". En d'autres termes, vous multipliez le numérateur d'une fraction par le dénominateur de l'autre et vice versa, puis vous mettez ces deux réponses égales et vous résolvez.[3] 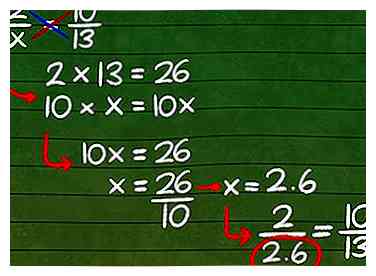 3 Introduire une variable. Étant donné que la multiplication croisée est le moyen le plus simple de déterminer des fractions équivalentes lorsque vous devez résoudre une variable, ajoutons une variable.
3 Introduire une variable. Étant donné que la multiplication croisée est le moyen le plus simple de déterminer des fractions équivalentes lorsque vous devez résoudre une variable, ajoutons une variable.  4 Utilisez la multiplication croisée pour les équations avec plusieurs variables ou expressions de variable. L'une des meilleures choses à propos de la multiplication croisée est qu'elle fonctionne essentiellement de la même manière, que vous traitiez de deux fractions simples (comme ci-dessus) ou de fractions plus complexes. Par exemple, si les deux fractions contiennent des variables, il vous suffit d'éliminer ces variables à la fin du processus de résolution. De même, si les numérateurs ou les dénominateurs de vos fractions contiennent des expressions variables (telles que x + 1), il suffit de "multiplier" en utilisant la propriété distributive et de résoudre comme vous le feriez normalement.[4]
4 Utilisez la multiplication croisée pour les équations avec plusieurs variables ou expressions de variable. L'une des meilleures choses à propos de la multiplication croisée est qu'elle fonctionne essentiellement de la même manière, que vous traitiez de deux fractions simples (comme ci-dessus) ou de fractions plus complexes. Par exemple, si les deux fractions contiennent des variables, il vous suffit d'éliminer ces variables à la fin du processus de résolution. De même, si les numérateurs ou les dénominateurs de vos fractions contiennent des expressions variables (telles que x + 1), il suffit de "multiplier" en utilisant la propriété distributive et de résoudre comme vous le feriez normalement.[4]  1 Croix multiplier les deux fractions. Pour les problèmes d'équivalence nécessitant la formule quadratique, nous commençons toujours par utiliser la multiplication croisée. Cependant, toute multiplication croisée impliquant la multiplication de termes variables par d'autres termes variables est susceptible d'entraîner une expression difficile à résoudre par l'algèbre. Dans de tels cas, vous devrez peut-être utiliser des techniques telles que l'affacturage et / ou la formule quadratique.[5]
1 Croix multiplier les deux fractions. Pour les problèmes d'équivalence nécessitant la formule quadratique, nous commençons toujours par utiliser la multiplication croisée. Cependant, toute multiplication croisée impliquant la multiplication de termes variables par d'autres termes variables est susceptible d'entraîner une expression difficile à résoudre par l'algèbre. Dans de tels cas, vous devrez peut-être utiliser des techniques telles que l'affacturage et / ou la formule quadratique.[5]  2 Exprimez l'équation comme une équation quadratique. À ce stade, nous voulons exprimer cette équation sous forme quadratique (ax2 + bx + c = 0), ce que nous faisons en réglant l’équation à zéro. Dans ce cas, nous soustrayons 12 des deux côtés pour obtenir 2x2 - 14 = 0.
2 Exprimez l'équation comme une équation quadratique. À ce stade, nous voulons exprimer cette équation sous forme quadratique (ax2 + bx + c = 0), ce que nous faisons en réglant l’équation à zéro. Dans ce cas, nous soustrayons 12 des deux côtés pour obtenir 2x2 - 14 = 0.  3 Résoudre en branchant les nombres de votre équation quadratique dans la formule quadratique. La formule quadratique (x = (-b +/- √ (b2 - 4ac)) / 2a) nous aidera à résoudre notre valeur x à ce stade.[6] Ne soyez pas intimidé par la longueur de la formule. Vous prenez simplement les valeurs de votre équation quadratique à l'étape deux et les connectez aux endroits appropriés avant de les résoudre.
3 Résoudre en branchant les nombres de votre équation quadratique dans la formule quadratique. La formule quadratique (x = (-b +/- √ (b2 - 4ac)) / 2a) nous aidera à résoudre notre valeur x à ce stade.[6] Ne soyez pas intimidé par la longueur de la formule. Vous prenez simplement les valeurs de votre équation quadratique à l'étape deux et les connectez aux endroits appropriés avant de les résoudre. 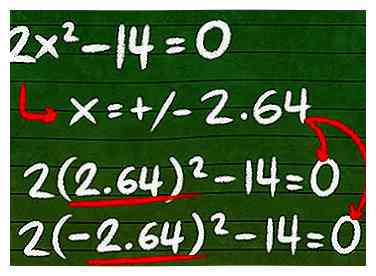 4 Vérifiez votre réponse en branchant la valeur x dans votre équation quadratique. En branchant la valeur calculée de x dans votre équation quadratique de l'étape deux, vous pouvez facilement déterminer si vous avez atteint la bonne réponse.[7] Dans cet exemple, vous branchez à la fois 2,64 et -2,64 dans l’équation quadratique originale.
4 Vérifiez votre réponse en branchant la valeur x dans votre équation quadratique. En branchant la valeur calculée de x dans votre équation quadratique de l'étape deux, vous pouvez facilement déterminer si vous avez atteint la bonne réponse.[7] Dans cet exemple, vous branchez à la fois 2,64 et -2,64 dans l’équation quadratique originale.