Diviser une fraction par une fraction peut sembler déroutant au début, mais c'est vraiment très simple. Tout ce que vous devez faire est de retourner les deuxièmes fractions, multiplier et réduire! Cet article vous guidera à travers le processus et vous montrera que la division des fractions par fractions est vraiment un jeu d'enfant.
Première partie de deux:
Comprendre comment diviser les fractions par fractions
-
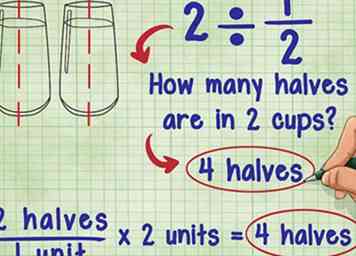 1 Pensez à ce que signifie la division par une fraction. Le problème 2 ÷ 1/2 vous demande: "Combien de moitiés sont dans 2?"
1 Pensez à ce que signifie la division par une fraction. Le problème 2 ÷ 1/2 vous demande: "Combien de moitiés sont dans 2?" - Essayez de penser à la même équation en termes de tasses d’eau: combien de demi-tasses d’eau y a-t-il dans deux tasses d’eau? Vous pouvez verser 2 demi-tasses d'eau dans chaque tasse d'eau, ce qui signifie que vous les ajoutez essentiellement et que vous avez deux tasses: 2 moitiés / 1 tasse * 2 tasses = 4 moitiés.
- Tout cela signifie que lorsque la fraction que vous divisez par est entre 0 et 1, la réponse sera toujours plus grande que le nombre original! Cela est vrai que vous divisiez des nombres entiers ou des fractions par une fraction.
-
 2 Comprenez que la division est le contraire de la multiplication. Par conséquent, la division par une fraction peut être réalisée en multipliant par son réciproque. L'inverse d'une fraction (aussi appelée son «inverse multiplicatif») est simplement la fraction retournée, de sorte que le numérateur et le dénominateur ont changé de place.[1] En un instant, nous allons diviser les fractions par des fractions en trouvant l’inverse de la deuxième fraction et en les multipliant, mais regardons d’abord les réciproques:
2 Comprenez que la division est le contraire de la multiplication. Par conséquent, la division par une fraction peut être réalisée en multipliant par son réciproque. L'inverse d'une fraction (aussi appelée son «inverse multiplicatif») est simplement la fraction retournée, de sorte que le numérateur et le dénominateur ont changé de place.[1] En un instant, nous allons diviser les fractions par des fractions en trouvant l’inverse de la deuxième fraction et en les multipliant, mais regardons d’abord les réciproques: - La réciproque de 3/4 est 4/3.
- La réciproque de 7/5 est 5/7.
- La réciproque de 1/2 est 2/1, ou 2.
-
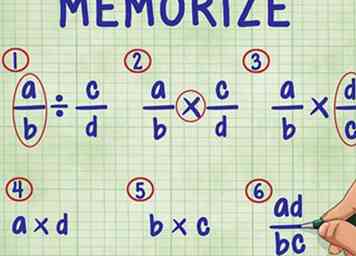 3 Mémorisez les étapes suivantes pour diviser une fraction par une fraction. Dans l'ordre, les étapes sont les suivantes:
3 Mémorisez les étapes suivantes pour diviser une fraction par une fraction. Dans l'ordre, les étapes sont les suivantes: - Laissez la première fraction de l'équation seule.
- Tournez le signe de division dans un signe de multiplication.
- Retournez la deuxième fraction (trouvez sa réciproque).
- Multipliez les numérateurs (chiffres du haut) des deux fractions ensemble. Ce résultat sera le numérateur (partie supérieure) de votre réponse. [2]
- Multipliez les dénominateurs (chiffres du bas) des deux fractions ensemble. Le résultat sera le dénominateur de votre réponse.
- Simplifiez votre fraction en la réduisant aux termes les plus simples.
-
 4 Suivez ces étapes sur l'exemple 1/3 ÷ 2/5. Nous allons commencer par laisser la première fraction seule et changer le signe de division en un signe de multiplication:
4 Suivez ces étapes sur l'exemple 1/3 ÷ 2/5. Nous allons commencer par laisser la première fraction seule et changer le signe de division en un signe de multiplication: - 1/3 ÷ 2/5 = devient:
- 1/3 * __ =
- Maintenant, retournez la seconde fraction (2/5) pour trouver sa réciproque, 5/2:
- 1/3 * 5/2 =
- Maintenant, multipliez les numérateurs (chiffres du haut) des deux fractions, 1 * 5 = 5.
- 1/3 * 5/2 = 5/
- Maintenant, multipliez les dénominateurs (chiffres du bas) des deux fractions, 3 * 2 = 6.
- Nous avons maintenant: 1/3 * 5/2 = 5/6
- Cette fraction particulière ne peut pas être simplifiée davantage, nous avons donc notre réponse.
-
 5 Essayez de vous souvenir de la comptine suivante pour vous rappeler: "Fractionner des fractions, aussi simple que du gâteau, retournez la deuxième fraction, puis multipliez. Et n'oubliez pas de simplifier, avant qu'il ne soit temps de dire au revoir." [3]
5 Essayez de vous souvenir de la comptine suivante pour vous rappeler: "Fractionner des fractions, aussi simple que du gâteau, retournez la deuxième fraction, puis multipliez. Et n'oubliez pas de simplifier, avant qu'il ne soit temps de dire au revoir." [3] - Un autre dicton utile qui vous dit quoi faire avec chaque partie de l'équation est:Laisse-moi (la première fraction), Change moi (le symbole de la division), Tourne moi (la deuxième fraction). "
Deuxième partie de deux:
Division de fractions par fractions en action
-
 1 Commencez par un exemple de problème. Utilisons 2/3 ÷ 3/7. Cette question nous demande combien de parties égales à 3/7 d'un ensemble peuvent être trouvées dans la valeur 2/3. Ne t'inquiète pas; ce n'est pas aussi dur que ça en a l'air!
1 Commencez par un exemple de problème. Utilisons 2/3 ÷ 3/7. Cette question nous demande combien de parties égales à 3/7 d'un ensemble peuvent être trouvées dans la valeur 2/3. Ne t'inquiète pas; ce n'est pas aussi dur que ça en a l'air! -
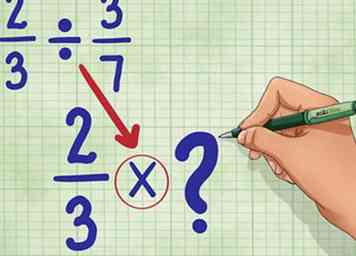 2 Changez le signe de division en un signe de multiplication. Votre nouvelle équation devrait se lire comme suit: 2/3 * __ (nous remplirons le blanc dans un instant.)
2 Changez le signe de division en un signe de multiplication. Votre nouvelle équation devrait se lire comme suit: 2/3 * __ (nous remplirons le blanc dans un instant.) -
 3 Maintenant, trouvez l'inverse de la deuxième fraction. Cela signifie qu'il faut retourner 3/7 pour que le numérateur (3) soit maintenant en bas et le dénominateur (7) en haut. La réciproque de 3/7 est 7/3. Maintenant, écrivez votre nouvelle équation:
3 Maintenant, trouvez l'inverse de la deuxième fraction. Cela signifie qu'il faut retourner 3/7 pour que le numérateur (3) soit maintenant en bas et le dénominateur (7) en haut. La réciproque de 3/7 est 7/3. Maintenant, écrivez votre nouvelle équation: - 2/3 * 7/3 = __
-
 4 Multipliez vos fractions. Multipliez d'abord les numérateurs des deux fractions ensemble: 2 * 7 = 14. 14 est le numérateur (valeur supérieure) de votre réponse. Multipliez ensuite les dénominateurs des deux fractions ensemble: 3 * 3 = 9. 9 est le dénominateur (valeur inférieure) de votre réponse. Vous savez maintenant que 2/3 * 7/3 = 14/9.
4 Multipliez vos fractions. Multipliez d'abord les numérateurs des deux fractions ensemble: 2 * 7 = 14. 14 est le numérateur (valeur supérieure) de votre réponse. Multipliez ensuite les dénominateurs des deux fractions ensemble: 3 * 3 = 9. 9 est le dénominateur (valeur inférieure) de votre réponse. Vous savez maintenant que 2/3 * 7/3 = 14/9. -
 5 Simplifiez votre fraction. Dans ce cas, comme le numérateur de la fraction est plus grand que le dénominateur, nous savons que notre fraction est supérieure à 1, et nous devrions la convertir en une fraction mixte. (Une fraction mixte est un nombre entier et une fraction combinée, comme 1 2/3.[4])
5 Simplifiez votre fraction. Dans ce cas, comme le numérateur de la fraction est plus grand que le dénominateur, nous savons que notre fraction est supérieure à 1, et nous devrions la convertir en une fraction mixte. (Une fraction mixte est un nombre entier et une fraction combinée, comme 1 2/3.[4]) - D'abord diviser le numérateur 14 par 9. 9 va à 14 une fois, avec un reste de 5, donc vous devriez écrire votre fraction réduite comme: 1 5/9 («Un et cinq neuvièmes»).
- Arrêtez là, vous avez trouvé votre réponse! Vous pouvez déterminer que vous ne pouvez pas réduire davantage la fraction car le dénominateur n'est pas divisible par le numérateur (9 ne peut pas être divisé par 5) et le numérateur est un nombre premier, ou un nombre entier divisible par un seul.[5]
-
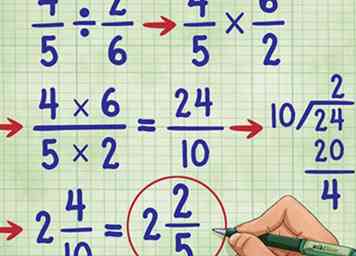 6 Essayez un autre exemple! Essayons le problème 4/5 ÷ 2/6 =. Commencez par changer le signe de division en un signe de multiplication (4/5 * __ = ), puis trouvez l'inverse de 2/6, qui est 6/2. Vous savez avoir l'équation: 4/5 * 6/2 =__. Maintenant, multipliez les numérateurs, 4 * 6 = 24et les dénominateurs 5* 2 = 10. Vous avez maintenant4/5 * 6/2 = 24/10. Maintenant, simplifiez la fraction. Comme le numérateur est plus grand que le dénominateur, nous devrons le convertir en une fraction mixte.
6 Essayez un autre exemple! Essayons le problème 4/5 ÷ 2/6 =. Commencez par changer le signe de division en un signe de multiplication (4/5 * __ = ), puis trouvez l'inverse de 2/6, qui est 6/2. Vous savez avoir l'équation: 4/5 * 6/2 =__. Maintenant, multipliez les numérateurs, 4 * 6 = 24et les dénominateurs 5* 2 = 10. Vous avez maintenant4/5 * 6/2 = 24/10. Maintenant, simplifiez la fraction. Comme le numérateur est plus grand que le dénominateur, nous devrons le convertir en une fraction mixte. - D'abord diviser le numérateur par le dénominateur, (24/10 = 2 reste 4).
- Ecrivez la réponse comme 2 4/10. Nous pourrions encore réduire cette fraction!
- Notez que 4 et 10 sont tous les deux des nombres pairs. La première étape pour les réduire est de les diviser par 2.On se retrouve avec 2/5.
- Comme le dénominateur (5) ne peut pas être divisé de manière égale par le numérateur (2), et qu’il est un nombre premier, nous savons qu’il ne peut pas être réduit davantage. Notre réponse est donc: 2 2/5.
-
 7 Obtenez de l'aide supplémentaire pour réduire les fractions. Vous avez probablement passé beaucoup de temps à apprendre à réduire les fractions avant d'essayer de les diviser les unes par les autres, mais si vous avez besoin d'un rappel ou d'une aide supplémentaire, il existe d'excellents articles en ligne. [6]
7 Obtenez de l'aide supplémentaire pour réduire les fractions. Vous avez probablement passé beaucoup de temps à apprendre à réduire les fractions avant d'essayer de les diviser les unes par les autres, mais si vous avez besoin d'un rappel ou d'une aide supplémentaire, il existe d'excellents articles en ligne. [6]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
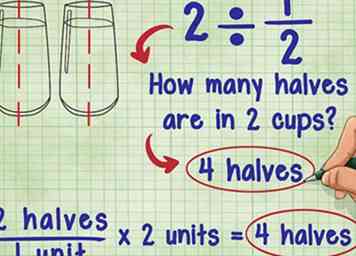 1 Pensez à ce que signifie la division par une fraction. Le problème 2 ÷ 1/2 vous demande: "Combien de moitiés sont dans 2?"
1 Pensez à ce que signifie la division par une fraction. Le problème 2 ÷ 1/2 vous demande: "Combien de moitiés sont dans 2?"  2 Comprenez que la division est le contraire de la multiplication. Par conséquent, la division par une fraction peut être réalisée en multipliant par son réciproque. L'inverse d'une fraction (aussi appelée son «inverse multiplicatif») est simplement la fraction retournée, de sorte que le numérateur et le dénominateur ont changé de place.[1] En un instant, nous allons diviser les fractions par des fractions en trouvant l’inverse de la deuxième fraction et en les multipliant, mais regardons d’abord les réciproques:
2 Comprenez que la division est le contraire de la multiplication. Par conséquent, la division par une fraction peut être réalisée en multipliant par son réciproque. L'inverse d'une fraction (aussi appelée son «inverse multiplicatif») est simplement la fraction retournée, de sorte que le numérateur et le dénominateur ont changé de place.[1] En un instant, nous allons diviser les fractions par des fractions en trouvant l’inverse de la deuxième fraction et en les multipliant, mais regardons d’abord les réciproques:  3 Mémorisez les étapes suivantes pour diviser une fraction par une fraction. Dans l'ordre, les étapes sont les suivantes:
3 Mémorisez les étapes suivantes pour diviser une fraction par une fraction. Dans l'ordre, les étapes sont les suivantes:  4 Suivez ces étapes sur l'exemple 1/3 ÷ 2/5. Nous allons commencer par laisser la première fraction seule et changer le signe de division en un signe de multiplication:
4 Suivez ces étapes sur l'exemple 1/3 ÷ 2/5. Nous allons commencer par laisser la première fraction seule et changer le signe de division en un signe de multiplication:  5 Essayez de vous souvenir de la comptine suivante pour vous rappeler: "Fractionner des fractions, aussi simple que du gâteau, retournez la deuxième fraction, puis multipliez. Et n'oubliez pas de simplifier, avant qu'il ne soit temps de dire au revoir." [3]
5 Essayez de vous souvenir de la comptine suivante pour vous rappeler: "Fractionner des fractions, aussi simple que du gâteau, retournez la deuxième fraction, puis multipliez. Et n'oubliez pas de simplifier, avant qu'il ne soit temps de dire au revoir." [3]  1 Commencez par un exemple de problème. Utilisons 2/3 ÷ 3/7. Cette question nous demande combien de parties égales à 3/7 d'un ensemble peuvent être trouvées dans la valeur 2/3. Ne t'inquiète pas; ce n'est pas aussi dur que ça en a l'air!
1 Commencez par un exemple de problème. Utilisons 2/3 ÷ 3/7. Cette question nous demande combien de parties égales à 3/7 d'un ensemble peuvent être trouvées dans la valeur 2/3. Ne t'inquiète pas; ce n'est pas aussi dur que ça en a l'air!  2 Changez le signe de division en un signe de multiplication. Votre nouvelle équation devrait se lire comme suit: 2/3 * __ (nous remplirons le blanc dans un instant.)
2 Changez le signe de division en un signe de multiplication. Votre nouvelle équation devrait se lire comme suit: 2/3 * __ (nous remplirons le blanc dans un instant.)  3 Maintenant, trouvez l'inverse de la deuxième fraction. Cela signifie qu'il faut retourner 3/7 pour que le numérateur (3) soit maintenant en bas et le dénominateur (7) en haut. La réciproque de 3/7 est 7/3. Maintenant, écrivez votre nouvelle équation:
3 Maintenant, trouvez l'inverse de la deuxième fraction. Cela signifie qu'il faut retourner 3/7 pour que le numérateur (3) soit maintenant en bas et le dénominateur (7) en haut. La réciproque de 3/7 est 7/3. Maintenant, écrivez votre nouvelle équation:  4 Multipliez vos fractions. Multipliez d'abord les numérateurs des deux fractions ensemble: 2 * 7 = 14. 14 est le numérateur (valeur supérieure) de votre réponse. Multipliez ensuite les dénominateurs des deux fractions ensemble: 3 * 3 = 9. 9 est le dénominateur (valeur inférieure) de votre réponse. Vous savez maintenant que 2/3 * 7/3 = 14/9.
4 Multipliez vos fractions. Multipliez d'abord les numérateurs des deux fractions ensemble: 2 * 7 = 14. 14 est le numérateur (valeur supérieure) de votre réponse. Multipliez ensuite les dénominateurs des deux fractions ensemble: 3 * 3 = 9. 9 est le dénominateur (valeur inférieure) de votre réponse. Vous savez maintenant que 2/3 * 7/3 = 14/9.  5 Simplifiez votre fraction. Dans ce cas, comme le numérateur de la fraction est plus grand que le dénominateur, nous savons que notre fraction est supérieure à 1, et nous devrions la convertir en une fraction mixte. (Une fraction mixte est un nombre entier et une fraction combinée, comme 1 2/3.[4])
5 Simplifiez votre fraction. Dans ce cas, comme le numérateur de la fraction est plus grand que le dénominateur, nous savons que notre fraction est supérieure à 1, et nous devrions la convertir en une fraction mixte. (Une fraction mixte est un nombre entier et une fraction combinée, comme 1 2/3.[4])  6 Essayez un autre exemple! Essayons le problème 4/5 ÷ 2/6 =. Commencez par changer le signe de division en un signe de multiplication (4/5 * __ = ), puis trouvez l'inverse de 2/6, qui est 6/2. Vous savez avoir l'équation: 4/5 * 6/2 =__. Maintenant, multipliez les numérateurs, 4 * 6 = 24et les dénominateurs 5* 2 = 10. Vous avez maintenant4/5 * 6/2 = 24/10. Maintenant, simplifiez la fraction. Comme le numérateur est plus grand que le dénominateur, nous devrons le convertir en une fraction mixte.
6 Essayez un autre exemple! Essayons le problème 4/5 ÷ 2/6 =. Commencez par changer le signe de division en un signe de multiplication (4/5 * __ = ), puis trouvez l'inverse de 2/6, qui est 6/2. Vous savez avoir l'équation: 4/5 * 6/2 =__. Maintenant, multipliez les numérateurs, 4 * 6 = 24et les dénominateurs 5* 2 = 10. Vous avez maintenant4/5 * 6/2 = 24/10. Maintenant, simplifiez la fraction. Comme le numérateur est plus grand que le dénominateur, nous devrons le convertir en une fraction mixte.  7 Obtenez de l'aide supplémentaire pour réduire les fractions. Vous avez probablement passé beaucoup de temps à apprendre à réduire les fractions avant d'essayer de les diviser les unes par les autres, mais si vous avez besoin d'un rappel ou d'une aide supplémentaire, il existe d'excellents articles en ligne. [6]
7 Obtenez de l'aide supplémentaire pour réduire les fractions. Vous avez probablement passé beaucoup de temps à apprendre à réduire les fractions avant d'essayer de les diviser les unes par les autres, mais si vous avez besoin d'un rappel ou d'une aide supplémentaire, il existe d'excellents articles en ligne. [6]