L'estimation (ou la supposition éclairée) peut être très utile pour les fractions. Si vous essayez de déterminer certaines proportions sans avoir les données ou le temps nécessaire pour obtenir une réponse précise, une estimation correcte vous mettra sur la bonne voie. Cependant, il y a une différence de taille entre faire des estimations et deviner à partir de rien. Si vous souhaitez optimiser vos chances de précision, vous devez examiner vos données de manière réfléchie.
Méthode One of Two:
Estimation des fractions mentalement
-
 1 Décidez si l'estimation est appropriée. L'estimation d'une fraction vous donnera l'essentiel de la fraction. Cependant, vous ne devinerez que rarement la réponse exacte. Si vous n'avez besoin que d'une idée générale de la réponse, les estimations sont utiles. Cependant, si vous devez donner une réponse exacte, résolvez votre équation avec des mesures exactes. Une bonne estimation transmettra rapidement l'idée générale et ne tentera pas de se faire passer pour une réponse exacte.
1 Décidez si l'estimation est appropriée. L'estimation d'une fraction vous donnera l'essentiel de la fraction. Cependant, vous ne devinerez que rarement la réponse exacte. Si vous n'avez besoin que d'une idée générale de la réponse, les estimations sont utiles. Cependant, si vous devez donner une réponse exacte, résolvez votre équation avec des mesures exactes. Une bonne estimation transmettra rapidement l'idée générale et ne tentera pas de se faire passer pour une réponse exacte. - Des exemples de situations qui favorisent les estimations comprennent la planification d'événements occasionnels (évaluation approximative des fournitures nécessaires), l'expression verbale d'une idée (diffusion de l'idée sans détails détaillés) ou certaines situations de cuisson telles que les ragoûts. produit.
-
 2 Simplifiez les fractions dans la mesure du possible.[1] Les fractions seront toujours plus faciles à gérer mentalement si vous les atteignez simplement à leur plus petit dénominateur commun. Une fraction listée 4/8, par exemple, peut être exprimée comme 2/4 ou 1/2. Ce sont différentes façons d'exprimer exactement la même fraction. C'est une bonne idée de simplifier vos fractions si possible afin de faciliter votre estimation. Trouver un nombre que vous pouvez diviser la moitié supérieure et inférieure d'une fraction par également. Les diviser par le même nombre réduira la taille des nombres, tout en gardant les proportions intactes.
2 Simplifiez les fractions dans la mesure du possible.[1] Les fractions seront toujours plus faciles à gérer mentalement si vous les atteignez simplement à leur plus petit dénominateur commun. Une fraction listée 4/8, par exemple, peut être exprimée comme 2/4 ou 1/2. Ce sont différentes façons d'exprimer exactement la même fraction. C'est une bonne idée de simplifier vos fractions si possible afin de faciliter votre estimation. Trouver un nombre que vous pouvez diviser la moitié supérieure et inférieure d'une fraction par également. Les diviser par le même nombre réduira la taille des nombres, tout en gardant les proportions intactes. - Les plus petits nombres sont généralement plus faciles à travailler que les grands nombres. Si tous les nombres inclus partagent un dénominateur commun, il est possible de les diviser en conséquence par cette racine. Par exemple, 4/16 et 6/8 peuvent être divisés par 4 et 2 respectivement. Cela se traduirait par 1/4 et 3/4.[2]
- D'une manière générale, si le haut et le bas de votre fraction sont égaux, vous pouvez diviser les deux côtés par 2. Les deux côtés seront deux fois moins gros que la précédente et la proportion restera la même.
- Assurez-vous de garder les deux côtés de votre fraction tout en divisant. Faire des fractions de fractions en divisant les dénominateurs de manière incorrecte rendra votre fraction beaucoup plus frustrante à gérer.
-
 3 Arrondissez les fractions.[3] Arrondir les fractions les rend plus faciles à gérer. Si vous avez une fraction qui ne peut pas être simplifiée telle quelle, le déplacer légèrement vers le haut ou le bas peut vous permettre de simplifier au prix de la réponse "exacte". Arrondir les fractions à la hausse ou à la baisse dépendra de beaucoup de choses, en particulier si vous avez affaire à un grand nombre de fractions très spécifiques et si le nombre de parties est insuffisant.
3 Arrondissez les fractions.[3] Arrondir les fractions les rend plus faciles à gérer. Si vous avez une fraction qui ne peut pas être simplifiée telle quelle, le déplacer légèrement vers le haut ou le bas peut vous permettre de simplifier au prix de la réponse "exacte". Arrondir les fractions à la hausse ou à la baisse dépendra de beaucoup de choses, en particulier si vous avez affaire à un grand nombre de fractions très spécifiques et si le nombre de parties est insuffisant. - "Arrondir" une fraction signifie l'amener légèrement en haut ou en bas pour que la fraction puisse être simplifiée. Par exemple, 7/16 peut être une fraction délicate à visualiser mentalement, mais si vous arrondissez légèrement à 8/16, cela devient exactement la moitié (1/2) de l'ensemble.
-
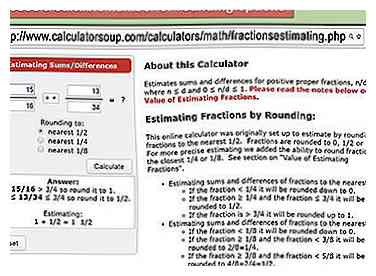 4 Choisissez un nombre approprié d'options d'arrondi. Si vous avez l'intention d'utiliser les mathématiques mentales, essayez de arrondir vos fractions à des proportions qui vous conviennent le mieux. Parce que les compétences personnelles en mathématiques mentales dépendent de l'individu, vous pouvez faire en sorte que l'arrondi soit grand ou petit, comme vous le souhaitez. Arrondir à la moitié (0, 1/2, 1) n'a de sens que pour les fractions les plus simples, tandis que des proportions plus complexes bénéficieront d'un plus grand nombre d'options d'arrondi.
4 Choisissez un nombre approprié d'options d'arrondi. Si vous avez l'intention d'utiliser les mathématiques mentales, essayez de arrondir vos fractions à des proportions qui vous conviennent le mieux. Parce que les compétences personnelles en mathématiques mentales dépendent de l'individu, vous pouvez faire en sorte que l'arrondi soit grand ou petit, comme vous le souhaitez. Arrondir à la moitié (0, 1/2, 1) n'a de sens que pour les fractions les plus simples, tandis que des proportions plus complexes bénéficieront d'un plus grand nombre d'options d'arrondi. - Arrondir vos fractions en portions plus petites (comme les huitièmes ou les seizièmes) peut être plus difficile selon votre niveau de compétence, mais vous constaterez que votre réponse est plus proche de la vraie réponse.[4]
-
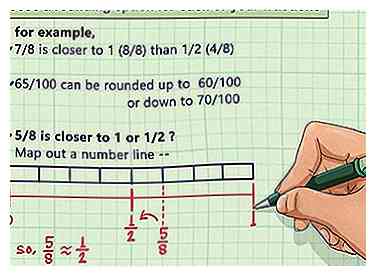 5 Choisissez une option d'arrondi pour chacune de vos fractions. La plupart du temps, une fraction sera plus proche de l'une des options d'arrondi adjacentes que l'autre. 7/8, par exemple, est plus proche de 1 (8/8) que 1/2 (4/8). Dans certains cas, cependant, il peut se situer quelque part au milieu. Une fraction comme 65/100 peut être arrondie à 60/100 ou 70/100. Vous pouvez prendre une décision qui, selon vous, représente le mieux les données fournies. Tracer une ligne numérique vous aidera à indiquer visuellement l’option d’arrondi la plus proche d’une fraction.[5]
5 Choisissez une option d'arrondi pour chacune de vos fractions. La plupart du temps, une fraction sera plus proche de l'une des options d'arrondi adjacentes que l'autre. 7/8, par exemple, est plus proche de 1 (8/8) que 1/2 (4/8). Dans certains cas, cependant, il peut se situer quelque part au milieu. Une fraction comme 65/100 peut être arrondie à 60/100 ou 70/100. Vous pouvez prendre une décision qui, selon vous, représente le mieux les données fournies. Tracer une ligne numérique vous aidera à indiquer visuellement l’option d’arrondi la plus proche d’une fraction.[5] - Bien que cela puisse aller de soi, vous n’aurez rien à faire avec les fractions qui tombent déjà dans l’une de vos options d’arrondi.
-
 6 Gardez à l'esprit vos changements d'arrondi. Bien que l'arrondissement des fractions puisse être utile pour estimer, il est important que vous ne preniez pas ces nouvelles proportions comme un rapport précis des proportions réelles.[6] Gardez les fractions originales et précises à portée de main. Avoir à la fois les versions exactes et les versions estimées disponibles est utile, car vous serez capable de communiquer l’idée facilement, ainsi que de la sauvegarder en cas de besoin.
6 Gardez à l'esprit vos changements d'arrondi. Bien que l'arrondissement des fractions puisse être utile pour estimer, il est important que vous ne preniez pas ces nouvelles proportions comme un rapport précis des proportions réelles.[6] Gardez les fractions originales et précises à portée de main. Avoir à la fois les versions exactes et les versions estimées disponibles est utile, car vous serez capable de communiquer l’idée facilement, ainsi que de la sauvegarder en cas de besoin. -
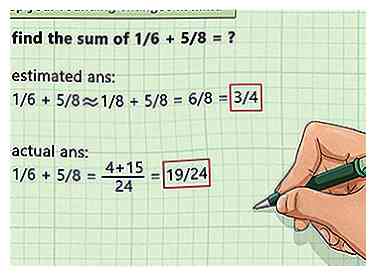
 7 Comparez votre estimation avec les fractions précises. Une fois que vous avez une estimation arrondie et simplifiée, vous pouvez affiner votre estimation en la plaçant contre la fraction d'origine. De cette façon, vous pouvez identifier comment votre estimation peut varier du nombre réel. Bien qu'une estimation soit un excellent moyen de visualiser ou d'analyser les données de manière large, vous devriez réfléchir à la distance réelle de votre fraction.
7 Comparez votre estimation avec les fractions précises. Une fois que vous avez une estimation arrondie et simplifiée, vous pouvez affiner votre estimation en la plaçant contre la fraction d'origine. De cette façon, vous pouvez identifier comment votre estimation peut varier du nombre réel. Bien qu'une estimation soit un excellent moyen de visualiser ou d'analyser les données de manière large, vous devriez réfléchir à la distance réelle de votre fraction. - Une fraction de 7/16 pourrait être arrondie à 8/16 (ou 1/2). 7/16 peut encore être vu en gros, mais vous devez vous rappeler que la version simplifiée est légèrement supérieure au nombre réel. Une manière mathématique d'exprimer cela serait: (1/2 - 1/16).
Méthode deux sur deux:
Estimation des fractions visuelles
-
 1 Mesurer la validité d'une estimation visuelle. Communiquer une fraction visuellement le rend apparent aux autres. Ils sont un moyen idéal d'exprimer des proportions aux autres, surtout si ces personnes n'ont pas de formation en mathématiques. Les estimations visuelles sont les mieux adaptées pour comparer une fraction à une autre. L'œil humain est formé pour comparer et mesurer des choses, même sans expérience mathématique. Mettre quelque chose en termes visuels aide à s’éloigner de la pensée purement abstraite basée sur les chiffres. Les estimations visuelles sont également parfaites pour une utilisation dans des environnements occasionnels et «réels».[7]
1 Mesurer la validité d'une estimation visuelle. Communiquer une fraction visuellement le rend apparent aux autres. Ils sont un moyen idéal d'exprimer des proportions aux autres, surtout si ces personnes n'ont pas de formation en mathématiques. Les estimations visuelles sont les mieux adaptées pour comparer une fraction à une autre. L'œil humain est formé pour comparer et mesurer des choses, même sans expérience mathématique. Mettre quelque chose en termes visuels aide à s’éloigner de la pensée purement abstraite basée sur les chiffres. Les estimations visuelles sont également parfaites pour une utilisation dans des environnements occasionnels et «réels».[7] - Par exemple, une fraction de 12/16 peut sembler plus grande que 7/8 sous une forme purement numérique, mais un simple graphique des deux à côté montrera facilement que ce dernier est plus grand que le précédent.
- Les deux principaux types de fractions illustrées visuellement sont les graphiques linéaires et circulaires.[8] Les lignes sont les meilleures pour les mesures, tandis que les cercles (ou les «camemberts») sont les meilleurs pour montrer les proportions.
-
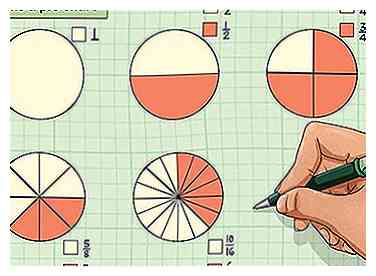
 2 Choisissez un modèle visuel.[9] Différents modèles visuels s'adapteront à différentes personnes. Que vous souhaitiez utiliser un graphique à secteurs, un rectangle, un graphique ou une autre manière de visualiser vos proportions, une illustration d'une fraction vous donnera un point de référence pour y réfléchir plus concrètement.
2 Choisissez un modèle visuel.[9] Différents modèles visuels s'adapteront à différentes personnes. Que vous souhaitiez utiliser un graphique à secteurs, un rectangle, un graphique ou une autre manière de visualiser vos proportions, une illustration d'une fraction vous donnera un point de référence pour y réfléchir plus concrètement. - Différentes proportions peuvent être indiquées par différentes nuances ou couleurs. Par exemple, deux tiers ombrés d'un cercle à secteurs indiquent une fraction de 2/3.
- C'est une bonne idée de jouer avec quelques modèles visuels utilisant le même ensemble de fractions. Cela vous montrera comment différents modèles peuvent représenter la même chose.
-
 3 Illustrer des fractions avec des morceaux physiques. En utilisant des morceaux de chocolat, des blocs de construction ou même des cailloux, vous pouvez estimer vos fractions en plaçant différents morceaux en groupes. Une fraction de 50 parties (17/50 + 33/50) peut être exprimée en séparant 50 pièces en deux groupes. Avec cela, vous serez en mesure de voir visuellement la taille d'une fraction à l'autre.
3 Illustrer des fractions avec des morceaux physiques. En utilisant des morceaux de chocolat, des blocs de construction ou même des cailloux, vous pouvez estimer vos fractions en plaçant différents morceaux en groupes. Une fraction de 50 parties (17/50 + 33/50) peut être exprimée en séparant 50 pièces en deux groupes. Avec cela, vous serez en mesure de voir visuellement la taille d'une fraction à l'autre. - En illustrant deux proportions ou plus les unes à côté des autres, vous aurez une référence visuelle facile sur les fractions les plus grandes et les plus petites. L'œil humain sera en mesure d'identifier la distinction presque sans réfléchir, c'est donc un bon moyen de le communiquer en termes clairs.[10]
-
 4 Empile tes proportions les unes à côté des autres.[11] Les fractions relatives sont tout autour de nous et nous faisons souvent des choix en estimant les fractions sans même y penser. Si vous cherchez un moyen de pratiquer votre estimation de fraction, placez deux objets de hauteur différente l'un à côté de l'autre. À partir de là, essayez de deviner quelle proportion de la taille de l'objet plus grand correspond à la plus petite.
4 Empile tes proportions les unes à côté des autres.[11] Les fractions relatives sont tout autour de nous et nous faisons souvent des choix en estimant les fractions sans même y penser. Si vous cherchez un moyen de pratiquer votre estimation de fraction, placez deux objets de hauteur différente l'un à côté de l'autre. À partir de là, essayez de deviner quelle proportion de la taille de l'objet plus grand correspond à la plus petite. - Vous pouvez vérifier vos réponses en plaçant une règle et en mesurant les dimensions appropriées de vos articles après le fait.
-
 5 Faire un camembert. Les camemberts sont un excellent moyen d'exprimer les proportions de manière visuelle. Si vous êtes un penseur visuel, c'est une bonne idée de travailler vos fractions arrondies dans un cercle. De là, vous pouvez exprimer votre estimation sans avoir à compter sur des chiffres arrondis qui peuvent ne pas être exacts. Contrairement aux graphiques (qui ont tendance à s'appuyer sur des données exactes), un graphique circulaire est censé être un moyen rapide de montrer des données visuelles. Il est généralement plus facile d'analyser visuellement les parties d'un cercle que les autres modèles visuels, car un cercle complet représente un tout.
5 Faire un camembert. Les camemberts sont un excellent moyen d'exprimer les proportions de manière visuelle. Si vous êtes un penseur visuel, c'est une bonne idée de travailler vos fractions arrondies dans un cercle. De là, vous pouvez exprimer votre estimation sans avoir à compter sur des chiffres arrondis qui peuvent ne pas être exacts. Contrairement aux graphiques (qui ont tendance à s'appuyer sur des données exactes), un graphique circulaire est censé être un moyen rapide de montrer des données visuelles. Il est généralement plus facile d'analyser visuellement les parties d'un cercle que les autres modèles visuels, car un cercle complet représente un tout.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Décidez si l'estimation est appropriée. L'estimation d'une fraction vous donnera l'essentiel de la fraction. Cependant, vous ne devinerez que rarement la réponse exacte. Si vous n'avez besoin que d'une idée générale de la réponse, les estimations sont utiles. Cependant, si vous devez donner une réponse exacte, résolvez votre équation avec des mesures exactes. Une bonne estimation transmettra rapidement l'idée générale et ne tentera pas de se faire passer pour une réponse exacte.
1 Décidez si l'estimation est appropriée. L'estimation d'une fraction vous donnera l'essentiel de la fraction. Cependant, vous ne devinerez que rarement la réponse exacte. Si vous n'avez besoin que d'une idée générale de la réponse, les estimations sont utiles. Cependant, si vous devez donner une réponse exacte, résolvez votre équation avec des mesures exactes. Une bonne estimation transmettra rapidement l'idée générale et ne tentera pas de se faire passer pour une réponse exacte.  2 Simplifiez les fractions dans la mesure du possible.[1] Les fractions seront toujours plus faciles à gérer mentalement si vous les atteignez simplement à leur plus petit dénominateur commun. Une fraction listée 4/8, par exemple, peut être exprimée comme 2/4 ou 1/2. Ce sont différentes façons d'exprimer exactement la même fraction. C'est une bonne idée de simplifier vos fractions si possible afin de faciliter votre estimation. Trouver un nombre que vous pouvez diviser la moitié supérieure et inférieure d'une fraction par également. Les diviser par le même nombre réduira la taille des nombres, tout en gardant les proportions intactes.
2 Simplifiez les fractions dans la mesure du possible.[1] Les fractions seront toujours plus faciles à gérer mentalement si vous les atteignez simplement à leur plus petit dénominateur commun. Une fraction listée 4/8, par exemple, peut être exprimée comme 2/4 ou 1/2. Ce sont différentes façons d'exprimer exactement la même fraction. C'est une bonne idée de simplifier vos fractions si possible afin de faciliter votre estimation. Trouver un nombre que vous pouvez diviser la moitié supérieure et inférieure d'une fraction par également. Les diviser par le même nombre réduira la taille des nombres, tout en gardant les proportions intactes.  3 Arrondissez les fractions.[3] Arrondir les fractions les rend plus faciles à gérer. Si vous avez une fraction qui ne peut pas être simplifiée telle quelle, le déplacer légèrement vers le haut ou le bas peut vous permettre de simplifier au prix de la réponse "exacte". Arrondir les fractions à la hausse ou à la baisse dépendra de beaucoup de choses, en particulier si vous avez affaire à un grand nombre de fractions très spécifiques et si le nombre de parties est insuffisant.
3 Arrondissez les fractions.[3] Arrondir les fractions les rend plus faciles à gérer. Si vous avez une fraction qui ne peut pas être simplifiée telle quelle, le déplacer légèrement vers le haut ou le bas peut vous permettre de simplifier au prix de la réponse "exacte". Arrondir les fractions à la hausse ou à la baisse dépendra de beaucoup de choses, en particulier si vous avez affaire à un grand nombre de fractions très spécifiques et si le nombre de parties est insuffisant.  4 Choisissez un nombre approprié d'options d'arrondi. Si vous avez l'intention d'utiliser les mathématiques mentales, essayez de arrondir vos fractions à des proportions qui vous conviennent le mieux. Parce que les compétences personnelles en mathématiques mentales dépendent de l'individu, vous pouvez faire en sorte que l'arrondi soit grand ou petit, comme vous le souhaitez. Arrondir à la moitié (0, 1/2, 1) n'a de sens que pour les fractions les plus simples, tandis que des proportions plus complexes bénéficieront d'un plus grand nombre d'options d'arrondi.
4 Choisissez un nombre approprié d'options d'arrondi. Si vous avez l'intention d'utiliser les mathématiques mentales, essayez de arrondir vos fractions à des proportions qui vous conviennent le mieux. Parce que les compétences personnelles en mathématiques mentales dépendent de l'individu, vous pouvez faire en sorte que l'arrondi soit grand ou petit, comme vous le souhaitez. Arrondir à la moitié (0, 1/2, 1) n'a de sens que pour les fractions les plus simples, tandis que des proportions plus complexes bénéficieront d'un plus grand nombre d'options d'arrondi.  5 Choisissez une option d'arrondi pour chacune de vos fractions. La plupart du temps, une fraction sera plus proche de l'une des options d'arrondi adjacentes que l'autre. 7/8, par exemple, est plus proche de 1 (8/8) que 1/2 (4/8). Dans certains cas, cependant, il peut se situer quelque part au milieu. Une fraction comme 65/100 peut être arrondie à 60/100 ou 70/100. Vous pouvez prendre une décision qui, selon vous, représente le mieux les données fournies. Tracer une ligne numérique vous aidera à indiquer visuellement l’option d’arrondi la plus proche d’une fraction.[5]
5 Choisissez une option d'arrondi pour chacune de vos fractions. La plupart du temps, une fraction sera plus proche de l'une des options d'arrondi adjacentes que l'autre. 7/8, par exemple, est plus proche de 1 (8/8) que 1/2 (4/8). Dans certains cas, cependant, il peut se situer quelque part au milieu. Une fraction comme 65/100 peut être arrondie à 60/100 ou 70/100. Vous pouvez prendre une décision qui, selon vous, représente le mieux les données fournies. Tracer une ligne numérique vous aidera à indiquer visuellement l’option d’arrondi la plus proche d’une fraction.[5]  6 Gardez à l'esprit vos changements d'arrondi. Bien que l'arrondissement des fractions puisse être utile pour estimer, il est important que vous ne preniez pas ces nouvelles proportions comme un rapport précis des proportions réelles.[6] Gardez les fractions originales et précises à portée de main. Avoir à la fois les versions exactes et les versions estimées disponibles est utile, car vous serez capable de communiquer l’idée facilement, ainsi que de la sauvegarder en cas de besoin.
6 Gardez à l'esprit vos changements d'arrondi. Bien que l'arrondissement des fractions puisse être utile pour estimer, il est important que vous ne preniez pas ces nouvelles proportions comme un rapport précis des proportions réelles.[6] Gardez les fractions originales et précises à portée de main. Avoir à la fois les versions exactes et les versions estimées disponibles est utile, car vous serez capable de communiquer l’idée facilement, ainsi que de la sauvegarder en cas de besoin.  7 Comparez votre estimation avec les fractions précises. Une fois que vous avez une estimation arrondie et simplifiée, vous pouvez affiner votre estimation en la plaçant contre la fraction d'origine. De cette façon, vous pouvez identifier comment votre estimation peut varier du nombre réel. Bien qu'une estimation soit un excellent moyen de visualiser ou d'analyser les données de manière large, vous devriez réfléchir à la distance réelle de votre fraction.
7 Comparez votre estimation avec les fractions précises. Une fois que vous avez une estimation arrondie et simplifiée, vous pouvez affiner votre estimation en la plaçant contre la fraction d'origine. De cette façon, vous pouvez identifier comment votre estimation peut varier du nombre réel. Bien qu'une estimation soit un excellent moyen de visualiser ou d'analyser les données de manière large, vous devriez réfléchir à la distance réelle de votre fraction.  1 Mesurer la validité d'une estimation visuelle. Communiquer une fraction visuellement le rend apparent aux autres. Ils sont un moyen idéal d'exprimer des proportions aux autres, surtout si ces personnes n'ont pas de formation en mathématiques. Les estimations visuelles sont les mieux adaptées pour comparer une fraction à une autre. L'œil humain est formé pour comparer et mesurer des choses, même sans expérience mathématique. Mettre quelque chose en termes visuels aide à s’éloigner de la pensée purement abstraite basée sur les chiffres. Les estimations visuelles sont également parfaites pour une utilisation dans des environnements occasionnels et «réels».[7]
1 Mesurer la validité d'une estimation visuelle. Communiquer une fraction visuellement le rend apparent aux autres. Ils sont un moyen idéal d'exprimer des proportions aux autres, surtout si ces personnes n'ont pas de formation en mathématiques. Les estimations visuelles sont les mieux adaptées pour comparer une fraction à une autre. L'œil humain est formé pour comparer et mesurer des choses, même sans expérience mathématique. Mettre quelque chose en termes visuels aide à s’éloigner de la pensée purement abstraite basée sur les chiffres. Les estimations visuelles sont également parfaites pour une utilisation dans des environnements occasionnels et «réels».[7]  2 Choisissez un modèle visuel.[9] Différents modèles visuels s'adapteront à différentes personnes. Que vous souhaitiez utiliser un graphique à secteurs, un rectangle, un graphique ou une autre manière de visualiser vos proportions, une illustration d'une fraction vous donnera un point de référence pour y réfléchir plus concrètement.
2 Choisissez un modèle visuel.[9] Différents modèles visuels s'adapteront à différentes personnes. Que vous souhaitiez utiliser un graphique à secteurs, un rectangle, un graphique ou une autre manière de visualiser vos proportions, une illustration d'une fraction vous donnera un point de référence pour y réfléchir plus concrètement.  3 Illustrer des fractions avec des morceaux physiques. En utilisant des morceaux de chocolat, des blocs de construction ou même des cailloux, vous pouvez estimer vos fractions en plaçant différents morceaux en groupes. Une fraction de 50 parties (17/50 + 33/50) peut être exprimée en séparant 50 pièces en deux groupes. Avec cela, vous serez en mesure de voir visuellement la taille d'une fraction à l'autre.
3 Illustrer des fractions avec des morceaux physiques. En utilisant des morceaux de chocolat, des blocs de construction ou même des cailloux, vous pouvez estimer vos fractions en plaçant différents morceaux en groupes. Une fraction de 50 parties (17/50 + 33/50) peut être exprimée en séparant 50 pièces en deux groupes. Avec cela, vous serez en mesure de voir visuellement la taille d'une fraction à l'autre.  4 Empile tes proportions les unes à côté des autres.[11] Les fractions relatives sont tout autour de nous et nous faisons souvent des choix en estimant les fractions sans même y penser. Si vous cherchez un moyen de pratiquer votre estimation de fraction, placez deux objets de hauteur différente l'un à côté de l'autre. À partir de là, essayez de deviner quelle proportion de la taille de l'objet plus grand correspond à la plus petite.
4 Empile tes proportions les unes à côté des autres.[11] Les fractions relatives sont tout autour de nous et nous faisons souvent des choix en estimant les fractions sans même y penser. Si vous cherchez un moyen de pratiquer votre estimation de fraction, placez deux objets de hauteur différente l'un à côté de l'autre. À partir de là, essayez de deviner quelle proportion de la taille de l'objet plus grand correspond à la plus petite.  5 Faire un camembert. Les camemberts sont un excellent moyen d'exprimer les proportions de manière visuelle. Si vous êtes un penseur visuel, c'est une bonne idée de travailler vos fractions arrondies dans un cercle. De là, vous pouvez exprimer votre estimation sans avoir à compter sur des chiffres arrondis qui peuvent ne pas être exacts. Contrairement aux graphiques (qui ont tendance à s'appuyer sur des données exactes), un graphique circulaire est censé être un moyen rapide de montrer des données visuelles. Il est généralement plus facile d'analyser visuellement les parties d'un cercle que les autres modèles visuels, car un cercle complet représente un tout.
5 Faire un camembert. Les camemberts sont un excellent moyen d'exprimer les proportions de manière visuelle. Si vous êtes un penseur visuel, c'est une bonne idée de travailler vos fractions arrondies dans un cercle. De là, vous pouvez exprimer votre estimation sans avoir à compter sur des chiffres arrondis qui peuvent ne pas être exacts. Contrairement aux graphiques (qui ont tendance à s'appuyer sur des données exactes), un graphique circulaire est censé être un moyen rapide de montrer des données visuelles. Il est généralement plus facile d'analyser visuellement les parties d'un cercle que les autres modèles visuels, car un cercle complet représente un tout.