Le rayon d'une sphère (abrégé en variable r ou R) est la distance entre le centre exact de la sphère et un point situé sur le bord extérieur de cette sphère. Comme pour les cercles, le rayon d'une sphère est souvent un élément essentiel pour le calcul du diamètre, de la circonférence, de la surface et / ou du volume de la forme. Cependant, vous pouvez également travailler en arrière à partir du diamètre, de la circonférence, etc. pour trouver le rayon de la sphère. Utilisez la formule qui fonctionne avec les informations que vous avez.
Méthode One of Three:
Utilisation de formules de calcul de rayon
-
 1 Trouvez le rayon si vous connaissez le diamètre. Le rayon est la moitié du diamètre, utilisez donc la formule r = D / 2. Ceci est identique à la méthode utilisée pour calculer le rayon d'un cercle à partir de son diamètre.[1]
1 Trouvez le rayon si vous connaissez le diamètre. Le rayon est la moitié du diamètre, utilisez donc la formule r = D / 2. Ceci est identique à la méthode utilisée pour calculer le rayon d'un cercle à partir de son diamètre.[1] - Si vous avez une sphère de 16 cm de diamètre, trouvez le rayon en divisant 16/2 pour obtenir 8 cm. Si le diamètre est 42, alors le rayon est 21.
-
 2 Trouvez le rayon si vous connaissez la circonférence. Utiliser la formule C / 2π. Puisque la circonférence est égale à πD, qui est égale à 2πr, la division de la circonférence de 2π donnera le rayon.[2]
2 Trouvez le rayon si vous connaissez la circonférence. Utiliser la formule C / 2π. Puisque la circonférence est égale à πD, qui est égale à 2πr, la division de la circonférence de 2π donnera le rayon.[2] - Si vous avez une sphère d'une circonférence de 20 m, trouvez le rayon en divisant 20 / 2π = 3,183 m.
- Utilisez la même formule pour convertir entre le rayon et la circonférence d'un cercle.
-
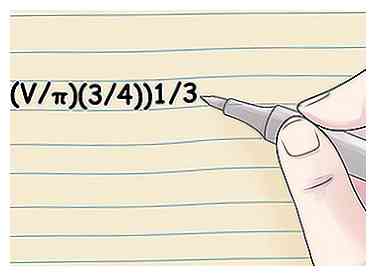 3 Calculez le rayon si vous connaissez le volume d'une sphère. Utilisez la formule ((V / π) (3/4))1/3.[3] Le volume d'une sphère est dérivé de l'équation V = (4/3) πr3. La résolution de la variable r dans cette équation obtient ((V / π) (3/4))1/3 = r, ce qui signifie que le rayon d'une sphère est égal au volume divisé par π, fois 3/4, tous pris au 1/3 (ou la racine du cube).[4]
3 Calculez le rayon si vous connaissez le volume d'une sphère. Utilisez la formule ((V / π) (3/4))1/3.[3] Le volume d'une sphère est dérivé de l'équation V = (4/3) πr3. La résolution de la variable r dans cette équation obtient ((V / π) (3/4))1/3 = r, ce qui signifie que le rayon d'une sphère est égal au volume divisé par π, fois 3/4, tous pris au 1/3 (ou la racine du cube).[4] - Si vous avez une sphère d'un volume de 100 pouces3, résolvez pour le rayon comme suit:
- ((V / π) (3/4))1/3 = r
- ((100/π)(3/4))1/3 = r
- ((31.83)(3/4))1/3 = r
- (23.87)1/3 = r
- 2,88 po = r
- Si vous avez une sphère d'un volume de 100 pouces3, résolvez pour le rayon comme suit:
-
 4 Trouvez le rayon de la surface. Utiliser la formule r = √ (A / (4π)). La surface d'une sphère est dérivée de l'équation A = 4πr2. Résoudre la variable r donne √ (A / (4π)) = r, ce qui signifie que le rayon d’une sphère est égal à la racine carrée de la surface divisée par 4π. Vous pouvez également prendre (A / (4π)) à la puissance 1/2 pour le même résultat.[5]
4 Trouvez le rayon de la surface. Utiliser la formule r = √ (A / (4π)). La surface d'une sphère est dérivée de l'équation A = 4πr2. Résoudre la variable r donne √ (A / (4π)) = r, ce qui signifie que le rayon d’une sphère est égal à la racine carrée de la surface divisée par 4π. Vous pouvez également prendre (A / (4π)) à la puissance 1/2 pour le même résultat.[5] - Si vous avez une sphère d'une surface de 1200 cm2, résolvez pour le rayon comme suit:
- √ (A / (4π)) = r
- √ (1200 / (4π)) = r
- √ (300 / (π)) = r
- √ (95,49) = r
- 9,77 cm = r
- Si vous avez une sphère d'une surface de 1200 cm2, résolvez pour le rayon comme suit:
Méthode deux sur trois:
Définition des concepts clés
-
 1 Identifier les mesures de base d'une sphère. Le rayon (r) est la distance entre le centre exact de la sphère et un point quelconque de la surface de la sphère. D'une manière générale, vous pouvez trouver le rayon d'une sphère si vous connaissez le diamètre, la circonférence, le volume ou la surface.
1 Identifier les mesures de base d'une sphère. Le rayon (r) est la distance entre le centre exact de la sphère et un point quelconque de la surface de la sphère. D'une manière générale, vous pouvez trouver le rayon d'une sphère si vous connaissez le diamètre, la circonférence, le volume ou la surface. - Diamètre (D): la distance à travers la sphère - le double du rayon. Le diamètre est la longueur d'une ligne passant par le centre de la sphère: d'un point à l'extérieur de la sphère à un point correspondant directement en face. En d'autres termes, la plus grande distance possible entre deux points de la sphère.
- Circonférence (C): la distance unidimensionnelle autour de la sphère à son point le plus large. En d'autres termes, le périmètre d'une section sphérique dont le plan passe par le centre de la sphère.
- Volume (V): l'espace tridimensionnel contenu dans la sphère. C'est "l'espace que la sphère occupe".[6]
- Surface (A): la surface à deux dimensions sur la surface extérieure de la sphère. La quantité d'espace plat qui couvre l'extérieur de la sphère.
- Pi (π): une constante qui exprime le rapport de la circonférence du cercle au diamètre du cercle. Les dix premiers chiffres de Pi sont toujours 3.141592653, bien qu'il soit généralement arrondi à 3.14.
-
 2 Utilisez différentes mesures pour trouver le rayon. Vous pouvez utiliser le diamètre, la circonférence, le volume et la surface pour calculer le rayon d'une sphère. Vous pouvez également calculer chacun de ces nombres si vous connaissez la longueur du rayon lui-même. Ainsi, pour trouver le rayon, essayez d’inverser les formules pour les calculs de ces composants. Découvrez les formules qui utilisent le rayon pour trouver le diamètre, la circonférence, le volume et la surface.
2 Utilisez différentes mesures pour trouver le rayon. Vous pouvez utiliser le diamètre, la circonférence, le volume et la surface pour calculer le rayon d'une sphère. Vous pouvez également calculer chacun de ces nombres si vous connaissez la longueur du rayon lui-même. Ainsi, pour trouver le rayon, essayez d’inverser les formules pour les calculs de ces composants. Découvrez les formules qui utilisent le rayon pour trouver le diamètre, la circonférence, le volume et la surface. - D = 2r. Comme pour les cercles, le diamètre d'une sphère est le double du rayon.
- C = πD ou 2πr. Comme pour les cercles, la circonférence d'une sphère est égale à π fois le diamètre. Puisque le diamètre est le double du rayon, on peut aussi dire que la circonférence est le double du rayon multiplié par π.
- V = (4/3) πr3. Le volume d'une sphère est le rayon cubé (multiplié par deux fois), multiplié par π, multiplié par 4/3.[7]
- A = 4πr2. La surface d'une sphère est le rayon carré (fois lui-même), fois π, fois 4. Puisque l'aire d'un cercle est πr2, on peut aussi dire que la surface d'une sphère est quatre fois supérieure à la surface du cercle formé par sa circonférence.
Méthode trois sur trois:
Trouver le rayon comme distance entre deux points
-
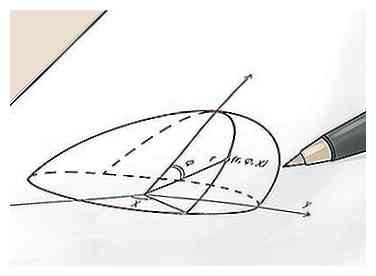 1 Trouvez les coordonnées (x, y, z) du point central de la sphère. Une façon de penser au rayon d'une sphère est la distance entre le point situé au centre de la sphère et un point quelconque de la surface de la sphère. Comme cela est vrai, si vous connaissez les coordonnées du point situé au centre de la sphère et de tout point de la surface, vous pouvez trouver le rayon de la sphère en calculant simplement la distance entre les deux points avec une variante de base. formule de distance. Pour commencer, trouvez les coordonnées du centre de la sphère. Notez que les sphères étant tridimensionnelles, il s'agira d'un point (x, y, z) plutôt que d'un point (x, y).
1 Trouvez les coordonnées (x, y, z) du point central de la sphère. Une façon de penser au rayon d'une sphère est la distance entre le point situé au centre de la sphère et un point quelconque de la surface de la sphère. Comme cela est vrai, si vous connaissez les coordonnées du point situé au centre de la sphère et de tout point de la surface, vous pouvez trouver le rayon de la sphère en calculant simplement la distance entre les deux points avec une variante de base. formule de distance. Pour commencer, trouvez les coordonnées du centre de la sphère. Notez que les sphères étant tridimensionnelles, il s'agira d'un point (x, y, z) plutôt que d'un point (x, y). - Ce processus est plus facile à comprendre en suivant un exemple. Pour notre propos, supposons que nous ayons une sphère centrée autour du point (x, y, z) (4, -1, 12). Dans les prochaines étapes, nous utiliserons ce point pour vous aider à trouver le rayon.
-
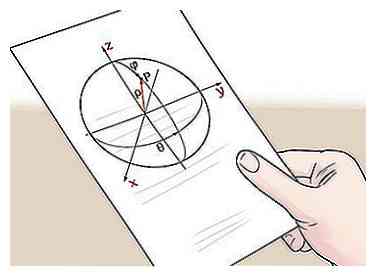 2 Trouvez les coordonnées d'un point sur la surface de la sphère. Ensuite, vous devrez trouver les coordonnées (x, y, z) d'un point sur la surface de la sphère. Cela peut être tout pointe sur la surface de la sphère. Étant donné que les points à la surface d'une sphère sont équidistants du point central par définition, tout point fonctionnera pour déterminer le rayon.
2 Trouvez les coordonnées d'un point sur la surface de la sphère. Ensuite, vous devrez trouver les coordonnées (x, y, z) d'un point sur la surface de la sphère. Cela peut être tout pointe sur la surface de la sphère. Étant donné que les points à la surface d'une sphère sont équidistants du point central par définition, tout point fonctionnera pour déterminer le rayon. - Aux fins de notre exemple de problème, disons que nous savons que le point (3, 3, 0) se trouve à la surface de la sphère. En calculant la distance entre ce point et le point central, on peut trouver le rayon.
-
 3 Trouvez le rayon avec la formule d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Maintenant que vous connaissez le centre de la sphère et un point sur la surface, le calcul de la distance entre les deux trouvera le rayon. Utilisez la formule de distance tridimensionnelle d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2), où d est égal à distance, (x1, y1, z1) est égal aux coordonnées du point central, et (x2, y2z2) est égal aux coordonnées du point sur la surface pour trouver la distance entre les deux points.
3 Trouvez le rayon avec la formule d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Maintenant que vous connaissez le centre de la sphère et un point sur la surface, le calcul de la distance entre les deux trouvera le rayon. Utilisez la formule de distance tridimensionnelle d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2), où d est égal à distance, (x1, y1, z1) est égal aux coordonnées du point central, et (x2, y2z2) est égal aux coordonnées du point sur la surface pour trouver la distance entre les deux points. - Dans notre exemple, nous raccorderions (4, -1, 12) pour (x1, y1z1) et (3, 3, 0) pour (x2, y2z2), en résolvant comme suit:
- d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2)
- d = √ ((3 - 4)2 + (3 - -1)2 + (0 - 12)2)
- d = √ ((- 1)2 + (4)2 + (-12)2)
- d = √ (1 + 16 + 144)
- d = √ (161)
- d = 12,69. C'est le rayon de notre sphère.
- Dans notre exemple, nous raccorderions (4, -1, 12) pour (x1, y1z1) et (3, 3, 0) pour (x2, y2z2), en résolvant comme suit:
-
 4 Sache que, dans les cas généraux, r = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Dans une sphère, chaque point de la surface de la sphère est à la même distance du point central. Si nous prenons la formule de distance tridimensionnelle ci-dessus et que nous remplaçons la variable "d" par la variable "r" pour le rayon, nous obtenons une forme de l’équation qui peut trouver le rayon donné1, y1z1) et tout point de surface correspondant (x2, y2z2).
4 Sache que, dans les cas généraux, r = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Dans une sphère, chaque point de la surface de la sphère est à la même distance du point central. Si nous prenons la formule de distance tridimensionnelle ci-dessus et que nous remplaçons la variable "d" par la variable "r" pour le rayon, nous obtenons une forme de l’équation qui peut trouver le rayon donné1, y1z1) et tout point de surface correspondant (x2, y2z2). - En cadrant les deux côtés de cette équation, nous obtenons r2 = (x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2. Notez que ceci est essentiellement égal à l'équation de base de la sphère r2 = x2 + y2 + z2 ce qui suppose un point central de (0,0,0).
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Trouvez le rayon si vous connaissez le diamètre. Le rayon est la moitié du diamètre, utilisez donc la formule r = D / 2. Ceci est identique à la méthode utilisée pour calculer le rayon d'un cercle à partir de son diamètre.[1]
1 Trouvez le rayon si vous connaissez le diamètre. Le rayon est la moitié du diamètre, utilisez donc la formule r = D / 2. Ceci est identique à la méthode utilisée pour calculer le rayon d'un cercle à partir de son diamètre.[1]  2 Trouvez le rayon si vous connaissez la circonférence. Utiliser la formule C / 2π. Puisque la circonférence est égale à πD, qui est égale à 2πr, la division de la circonférence de 2π donnera le rayon.[2]
2 Trouvez le rayon si vous connaissez la circonférence. Utiliser la formule C / 2π. Puisque la circonférence est égale à πD, qui est égale à 2πr, la division de la circonférence de 2π donnera le rayon.[2] 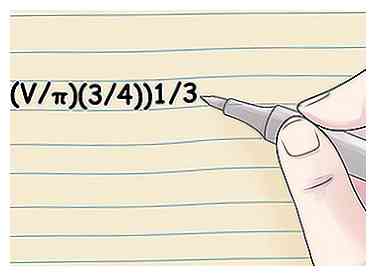 3 Calculez le rayon si vous connaissez le volume d'une sphère. Utilisez la formule ((V / π) (3/4))1/3.[3] Le volume d'une sphère est dérivé de l'équation V = (4/3) πr3. La résolution de la variable r dans cette équation obtient ((V / π) (3/4))1/3 = r, ce qui signifie que le rayon d'une sphère est égal au volume divisé par π, fois 3/4, tous pris au 1/3 (ou la racine du cube).[4]
3 Calculez le rayon si vous connaissez le volume d'une sphère. Utilisez la formule ((V / π) (3/4))1/3.[3] Le volume d'une sphère est dérivé de l'équation V = (4/3) πr3. La résolution de la variable r dans cette équation obtient ((V / π) (3/4))1/3 = r, ce qui signifie que le rayon d'une sphère est égal au volume divisé par π, fois 3/4, tous pris au 1/3 (ou la racine du cube).[4]  4 Trouvez le rayon de la surface. Utiliser la formule r = √ (A / (4π)). La surface d'une sphère est dérivée de l'équation A = 4πr2. Résoudre la variable r donne √ (A / (4π)) = r, ce qui signifie que le rayon d’une sphère est égal à la racine carrée de la surface divisée par 4π. Vous pouvez également prendre (A / (4π)) à la puissance 1/2 pour le même résultat.[5]
4 Trouvez le rayon de la surface. Utiliser la formule r = √ (A / (4π)). La surface d'une sphère est dérivée de l'équation A = 4πr2. Résoudre la variable r donne √ (A / (4π)) = r, ce qui signifie que le rayon d’une sphère est égal à la racine carrée de la surface divisée par 4π. Vous pouvez également prendre (A / (4π)) à la puissance 1/2 pour le même résultat.[5]  1 Identifier les mesures de base d'une sphère. Le rayon (r) est la distance entre le centre exact de la sphère et un point quelconque de la surface de la sphère. D'une manière générale, vous pouvez trouver le rayon d'une sphère si vous connaissez le diamètre, la circonférence, le volume ou la surface.
1 Identifier les mesures de base d'une sphère. Le rayon (r) est la distance entre le centre exact de la sphère et un point quelconque de la surface de la sphère. D'une manière générale, vous pouvez trouver le rayon d'une sphère si vous connaissez le diamètre, la circonférence, le volume ou la surface.  2 Utilisez différentes mesures pour trouver le rayon. Vous pouvez utiliser le diamètre, la circonférence, le volume et la surface pour calculer le rayon d'une sphère. Vous pouvez également calculer chacun de ces nombres si vous connaissez la longueur du rayon lui-même. Ainsi, pour trouver le rayon, essayez d’inverser les formules pour les calculs de ces composants. Découvrez les formules qui utilisent le rayon pour trouver le diamètre, la circonférence, le volume et la surface.
2 Utilisez différentes mesures pour trouver le rayon. Vous pouvez utiliser le diamètre, la circonférence, le volume et la surface pour calculer le rayon d'une sphère. Vous pouvez également calculer chacun de ces nombres si vous connaissez la longueur du rayon lui-même. Ainsi, pour trouver le rayon, essayez d’inverser les formules pour les calculs de ces composants. Découvrez les formules qui utilisent le rayon pour trouver le diamètre, la circonférence, le volume et la surface.  1 Trouvez les coordonnées (x, y, z) du point central de la sphère. Une façon de penser au rayon d'une sphère est la distance entre le point situé au centre de la sphère et un point quelconque de la surface de la sphère. Comme cela est vrai, si vous connaissez les coordonnées du point situé au centre de la sphère et de tout point de la surface, vous pouvez trouver le rayon de la sphère en calculant simplement la distance entre les deux points avec une variante de base. formule de distance. Pour commencer, trouvez les coordonnées du centre de la sphère. Notez que les sphères étant tridimensionnelles, il s'agira d'un point (x, y, z) plutôt que d'un point (x, y).
1 Trouvez les coordonnées (x, y, z) du point central de la sphère. Une façon de penser au rayon d'une sphère est la distance entre le point situé au centre de la sphère et un point quelconque de la surface de la sphère. Comme cela est vrai, si vous connaissez les coordonnées du point situé au centre de la sphère et de tout point de la surface, vous pouvez trouver le rayon de la sphère en calculant simplement la distance entre les deux points avec une variante de base. formule de distance. Pour commencer, trouvez les coordonnées du centre de la sphère. Notez que les sphères étant tridimensionnelles, il s'agira d'un point (x, y, z) plutôt que d'un point (x, y).  2 Trouvez les coordonnées d'un point sur la surface de la sphère. Ensuite, vous devrez trouver les coordonnées (x, y, z) d'un point sur la surface de la sphère. Cela peut être tout pointe sur la surface de la sphère. Étant donné que les points à la surface d'une sphère sont équidistants du point central par définition, tout point fonctionnera pour déterminer le rayon.
2 Trouvez les coordonnées d'un point sur la surface de la sphère. Ensuite, vous devrez trouver les coordonnées (x, y, z) d'un point sur la surface de la sphère. Cela peut être tout pointe sur la surface de la sphère. Étant donné que les points à la surface d'une sphère sont équidistants du point central par définition, tout point fonctionnera pour déterminer le rayon.  3 Trouvez le rayon avec la formule d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Maintenant que vous connaissez le centre de la sphère et un point sur la surface, le calcul de la distance entre les deux trouvera le rayon. Utilisez la formule de distance tridimensionnelle d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2), où d est égal à distance, (x1, y1, z1) est égal aux coordonnées du point central, et (x2, y2z2) est égal aux coordonnées du point sur la surface pour trouver la distance entre les deux points.
3 Trouvez le rayon avec la formule d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Maintenant que vous connaissez le centre de la sphère et un point sur la surface, le calcul de la distance entre les deux trouvera le rayon. Utilisez la formule de distance tridimensionnelle d = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2), où d est égal à distance, (x1, y1, z1) est égal aux coordonnées du point central, et (x2, y2z2) est égal aux coordonnées du point sur la surface pour trouver la distance entre les deux points.  4 Sache que, dans les cas généraux, r = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Dans une sphère, chaque point de la surface de la sphère est à la même distance du point central. Si nous prenons la formule de distance tridimensionnelle ci-dessus et que nous remplaçons la variable "d" par la variable "r" pour le rayon, nous obtenons une forme de l’équation qui peut trouver le rayon donné1, y1z1) et tout point de surface correspondant (x2, y2z2).
4 Sache que, dans les cas généraux, r = √ ((x2 - X1)2 + (y2 - y1)2 + (z2 - z1)2). Dans une sphère, chaque point de la surface de la sphère est à la même distance du point central. Si nous prenons la formule de distance tridimensionnelle ci-dessus et que nous remplaçons la variable "d" par la variable "r" pour le rayon, nous obtenons une forme de l’équation qui peut trouver le rayon donné1, y1z1) et tout point de surface correspondant (x2, y2z2).