Les opérations inverses sont couramment utilisées en algèbre pour simplifier ce qui pourrait autrement être difficile. Par exemple, si un problème vous oblige à diviser par une fraction, vous pouvez plus facilement le multiplier par sa réciproque. Ceci est une opération inverse. De même, comme il n'y a pas d'opérateur de division pour les matrices, vous devez multiplier par la matrice inverse. Calculer l'inverse d'une matrice 3x3 à la main est un travail fastidieux, mais qui mérite d'être revu. Vous pouvez également trouver l'inverse en utilisant une calculatrice graphique avancée.
Méthode One of Three:
Création de la matrice d'adjugate pour trouver la matrice inverse
-
 1 Vérifiez le déterminant de la matrice. Vous devez calculer le déterminant de la matrice comme étape initiale. Si le déterminant est 0, votre travail est terminé car la matrice n'a pas d'inverse. Le déterminant de la matrice M peut être représenté symboliquement par det (M).[1]
1 Vérifiez le déterminant de la matrice. Vous devez calculer le déterminant de la matrice comme étape initiale. Si le déterminant est 0, votre travail est terminé car la matrice n'a pas d'inverse. Le déterminant de la matrice M peut être représenté symboliquement par det (M).[1] - Pour une matrice 3x3, trouvez le déterminant en premier
- Pour examiner la recherche du déterminant d'une matrice, voir Trouver le déterminant d'une matrice 3X3.
-
 2 Transposer la matrice d'origine. Transposer signifie refléter la matrice autour de la diagonale principale ou, de manière équivalente, échanger le (i, j) ème élément et le (j, i) th. Lorsque vous transposez les termes de la matrice, vous devriez voir que la diagonale principale (de gauche à droite) est inchangée.[2]
2 Transposer la matrice d'origine. Transposer signifie refléter la matrice autour de la diagonale principale ou, de manière équivalente, échanger le (i, j) ème élément et le (j, i) th. Lorsque vous transposez les termes de la matrice, vous devriez voir que la diagonale principale (de gauche à droite) est inchangée.[2] - Une autre façon de penser à la transposition consiste à réécrire la première ligne en tant que première colonne, la deuxième en milieu de ligne et la troisième en troisième ligne. Notez les éléments colorés dans le diagramme ci-dessus et voyez où les nombres ont changé de position.
-
 3 Trouvez le déterminant de chacune des matrices 2x2 mineures. Chaque élément de la matrice 3x3 nouvellement transposée est associé à une matrice 2x2 correspondante «mineure». Pour trouver la matrice mineure correcte pour chaque terme, commencez par mettre en évidence la ligne et la colonne avec lesquelles vous avez commencé. Cela devrait inclure cinq termes de la matrice. Les quatre termes restants constituent la matrice mineure.[3]
3 Trouvez le déterminant de chacune des matrices 2x2 mineures. Chaque élément de la matrice 3x3 nouvellement transposée est associé à une matrice 2x2 correspondante «mineure». Pour trouver la matrice mineure correcte pour chaque terme, commencez par mettre en évidence la ligne et la colonne avec lesquelles vous avez commencé. Cela devrait inclure cinq termes de la matrice. Les quatre termes restants constituent la matrice mineure.[3] - Dans l'exemple ci-dessus, si vous voulez la matrice mineure du terme dans la deuxième ligne, première colonne, vous mettez en évidence les cinq termes qui sont dans la deuxième ligne et la première colonne. Les quatre termes restants sont la matrice mineure correspondante.
- Trouvez le déterminant de chaque matrice mineure en multipliant les diagonales et en soustrayant, comme indiqué.
- Pour plus d'informations sur les matrices mineures et leurs utilisations, voir Comprendre les bases des matrices.
-
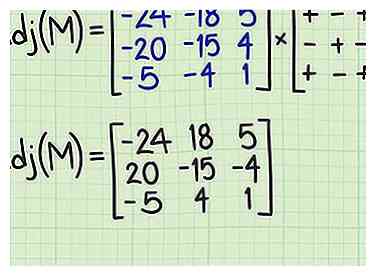 4 Créez la matrice de cofacteurs. Placer les résultats de l'étape précédente dans une nouvelle matrice de cofacteurs en alignant chaque déterminant de matrice mineur avec la position correspondante dans la matrice d'origine. Ainsi, le déterminant que vous avez calculé à partir de l'élément (1,1) de la matrice d'origine passe en position (1,1). Vous devez ensuite inverser le signe de l'alternance des termes de cette nouvelle matrice, en suivant le motif «damier» illustré.[4]
4 Créez la matrice de cofacteurs. Placer les résultats de l'étape précédente dans une nouvelle matrice de cofacteurs en alignant chaque déterminant de matrice mineur avec la position correspondante dans la matrice d'origine. Ainsi, le déterminant que vous avez calculé à partir de l'élément (1,1) de la matrice d'origine passe en position (1,1). Vous devez ensuite inverser le signe de l'alternance des termes de cette nouvelle matrice, en suivant le motif «damier» illustré.[4] - Lors de l'attribution de signes, le premier élément de la première ligne conserve son signe d'origine. Le deuxième élément est inversé. Le troisième élément conserve son signe original. Continuez avec le reste de la matrice de cette façon. Notez que les signes (+) ou (-) dans le diagramme en damier ne suggèrent pas que le terme final doit être positif ou négatif. Ce sont des indicateurs de maintien (+) ou d’inversion (-), quel que soit le signe du nombre.
- Pour une revue des cofacteurs, voir Comprendre les bases des matrices.
- Le résultat final de cette étape est appelé matrice auxiliaire de l'original. Ceci est parfois appelé la matrice adjointe. La matrice adjugée est notée Adj (M).
-
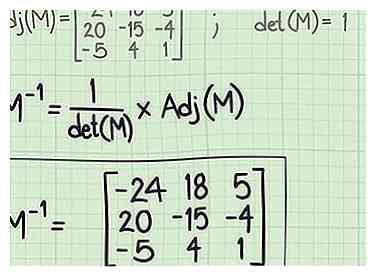 5 Diviser chaque terme de la matrice adjugate par le déterminant. Rappelez-vous le déterminant de M que vous avez calculé dans la première étape (pour vérifier que l'inverse était possible). Vous divisez maintenant chaque terme de la matrice par cette valeur. Placez le résultat de chaque calcul à l'endroit du terme d'origine. Le résultat est l'inverse de la matrice d'origine.[5]
5 Diviser chaque terme de la matrice adjugate par le déterminant. Rappelez-vous le déterminant de M que vous avez calculé dans la première étape (pour vérifier que l'inverse était possible). Vous divisez maintenant chaque terme de la matrice par cette valeur. Placez le résultat de chaque calcul à l'endroit du terme d'origine. Le résultat est l'inverse de la matrice d'origine.[5] - Pour la matrice d'échantillon présentée dans le diagramme, le facteur déterminant est 1. Par conséquent, la division de chaque terme de la matrice adjugée donne la matrice adjugée elle-même. (Vous ne serez pas toujours aussi chanceux.)
- Au lieu de se diviser, certaines sources représentent cette étape en multipliant chaque terme de M par 1 / det (M). Mathématiquement, ils sont équivalents.
Méthode deux sur trois:
Utilisation de la réduction linéaire des lignes pour trouver la matrice inverse
-
 1 Joindre la matrice d'identité à la matrice d'origine. Écrivez la matrice originale M, tracez une ligne verticale à sa droite, puis écrivez la matrice d'identité à droite de celle-ci. Vous devriez maintenant avoir ce qui semble être une matrice de trois lignes de six colonnes chacune.[6]
1 Joindre la matrice d'identité à la matrice d'origine. Écrivez la matrice originale M, tracez une ligne verticale à sa droite, puis écrivez la matrice d'identité à droite de celle-ci. Vous devriez maintenant avoir ce qui semble être une matrice de trois lignes de six colonnes chacune.[6] - Rappelons que la matrice d’identité est une matrice spéciale avec des 1 dans chaque position de la diagonale principale, de la gauche supérieure à la droite inférieure, et des 0 dans toutes les autres positions. Pour une revue de la matrice d'identité et de ses propriétés, voir Comprendre les bases des matrices.
-
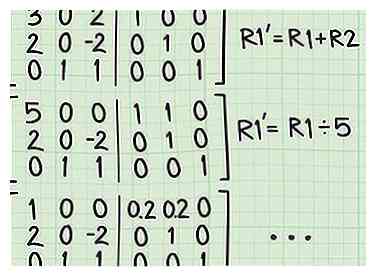 2 Effectuer des opérations de réduction de lignes linéaires. Votre objectif est de créer la matrice d'identité sur le côté gauche de cette nouvelle matrice augmentée. Au fur et à mesure que vous effectuez des étapes de réduction de ligne sur la gauche, vous devez effectuer systématiquement les mêmes opérations sur la droite, qui a commencé par votre matrice d'identité.[7]
2 Effectuer des opérations de réduction de lignes linéaires. Votre objectif est de créer la matrice d'identité sur le côté gauche de cette nouvelle matrice augmentée. Au fur et à mesure que vous effectuez des étapes de réduction de ligne sur la gauche, vous devez effectuer systématiquement les mêmes opérations sur la droite, qui a commencé par votre matrice d'identité.[7] - Rappelez-vous que les réductions de lignes sont effectuées sous la forme d'une combinaison de multiplication scalaire et d'addition ou de soustraction de lignes, afin d'isoler les termes individuels de la matrice. Pour un examen plus complet, voir Matrices de réduction de ligne.
-
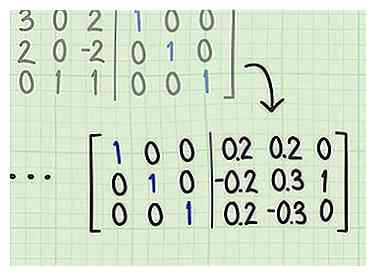 3 Continuez jusqu'à ce que vous formiez la matrice d'identité. Continuez à répéter les opérations de réduction des lignes linéaires jusqu'à ce que le côté gauche de votre matrice augmentée affiche la matrice d'identité (diagonale de 1s, avec les autres termes 0). Lorsque vous avez atteint ce point, le côté droit de votre séparateur vertical sera l'inverse de votre matrice d'origine.[8]
3 Continuez jusqu'à ce que vous formiez la matrice d'identité. Continuez à répéter les opérations de réduction des lignes linéaires jusqu'à ce que le côté gauche de votre matrice augmentée affiche la matrice d'identité (diagonale de 1s, avec les autres termes 0). Lorsque vous avez atteint ce point, le côté droit de votre séparateur vertical sera l'inverse de votre matrice d'origine.[8] -
 4 Écrivez la matrice inverse. Copiez les éléments qui apparaissent maintenant du côté droit du diviseur vertical en tant que matrice inverse.[9]
4 Écrivez la matrice inverse. Copiez les éléments qui apparaissent maintenant du côté droit du diviseur vertical en tant que matrice inverse.[9]
Méthode trois sur trois:
Utiliser une calculatrice pour trouver la matrice inverse
-
 1 Sélectionnez une calculatrice avec des capacités de matrice. Les simples calculatrices à 4 fonctions ne pourront pas vous aider à trouver directement l'inverse. Cependant, en raison de la nature répétitive des calculs, une calculatrice graphique avancée, telle que la Texas Instruments TI-83 ou TI-86, peut considérablement réduire le travail.[10]
1 Sélectionnez une calculatrice avec des capacités de matrice. Les simples calculatrices à 4 fonctions ne pourront pas vous aider à trouver directement l'inverse. Cependant, en raison de la nature répétitive des calculs, une calculatrice graphique avancée, telle que la Texas Instruments TI-83 ou TI-86, peut considérablement réduire le travail.[10] -
 2 Entrez votre matrice dans la calculatrice. Tout d'abord, entrez la fonction Matrix de votre calculatrice en appuyant sur la touche Matrix, si vous en avez une. Sur les calculatrices Texas Instruments, vous devrez peut-être appuyer sur 2nd Matrice.
2 Entrez votre matrice dans la calculatrice. Tout d'abord, entrez la fonction Matrix de votre calculatrice en appuyant sur la touche Matrix, si vous en avez une. Sur les calculatrices Texas Instruments, vous devrez peut-être appuyer sur 2nd Matrice. -
 3 Sélectionnez le sous-menu Modifier. Pour accéder au sous-menu, vous devrez peut-être utiliser les boutons fléchés ou choisir la touche de fonction appropriée en haut du clavier de votre calculatrice, en fonction de la disposition de votre calculatrice.[11]
3 Sélectionnez le sous-menu Modifier. Pour accéder au sous-menu, vous devrez peut-être utiliser les boutons fléchés ou choisir la touche de fonction appropriée en haut du clavier de votre calculatrice, en fonction de la disposition de votre calculatrice.[11] -
 4 Sélectionnez un nom pour votre matrice. La plupart des calculatrices sont équipées de 3 à 10 matrices, identifiées par les lettres A à J. En règle générale, choisissez simplement [A] pour travailler. Appuyez sur la touche Entrée après avoir effectué votre sélection.[12]
4 Sélectionnez un nom pour votre matrice. La plupart des calculatrices sont équipées de 3 à 10 matrices, identifiées par les lettres A à J. En règle générale, choisissez simplement [A] pour travailler. Appuyez sur la touche Entrée après avoir effectué votre sélection.[12] -
 5 Entrez les dimensions de votre matrice. Cet article se concentre sur les matrices 3x3. Cependant, la calculatrice peut gérer des tailles plus grandes. Entrez le nombre de lignes, puis appuyez sur Entrée, puis sur le nombre de colonnes et sur Entrée.[13]
5 Entrez les dimensions de votre matrice. Cet article se concentre sur les matrices 3x3. Cependant, la calculatrice peut gérer des tailles plus grandes. Entrez le nombre de lignes, puis appuyez sur Entrée, puis sur le nombre de colonnes et sur Entrée.[13] -
 6 Entrez chaque élément de la matrice. L'écran de la calculatrice affichera une matrice. Si vous travailliez auparavant avec la fonction matrice, la matrice précédente apparaîtra à l'écran. Le curseur mettra en évidence le premier élément de la matrice. Tapez la valeur de la matrice que vous souhaitez résoudre, puis entrez. Le curseur se déplacera automatiquement vers l'élément suivant de la matrice, en écrasant tous les numéros précédents.[14]
6 Entrez chaque élément de la matrice. L'écran de la calculatrice affichera une matrice. Si vous travailliez auparavant avec la fonction matrice, la matrice précédente apparaîtra à l'écran. Le curseur mettra en évidence le premier élément de la matrice. Tapez la valeur de la matrice que vous souhaitez résoudre, puis entrez. Le curseur se déplacera automatiquement vers l'élément suivant de la matrice, en écrasant tous les numéros précédents.[14] - Si vous souhaitez entrer un nombre négatif, utilisez le bouton négatif de votre calculatrice (-) et non la touche moins. La fonction de matrice ne lira pas correctement le numéro.
- Si nécessaire, vous pouvez utiliser les touches fléchées de votre calculatrice pour sauter autour de la matrice.
-
 7 Quittez la fonction Matrix. Après avoir entré toutes les valeurs de la matrice, appuyez sur la touche Quitter (ou 2nd Quittez, si nécessaire). Cela vous quittera de la fonction Matrix et vous ramènera à l'écran d'affichage principal de votre calculatrice.[15]
7 Quittez la fonction Matrix. Après avoir entré toutes les valeurs de la matrice, appuyez sur la touche Quitter (ou 2nd Quittez, si nécessaire). Cela vous quittera de la fonction Matrix et vous ramènera à l'écran d'affichage principal de votre calculatrice.[15] -
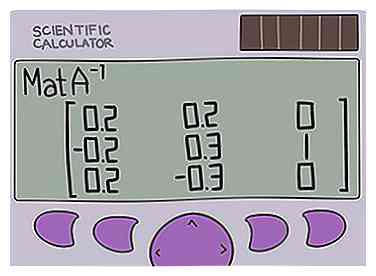 8 Utilisez la clé inverse pour trouver la matrice inverse. Tout d'abord, rouvrez la fonction Matrix et utilisez le bouton Noms pour sélectionner l'étiquette de matrice que vous avez utilisée pour définir votre matrice (probablement [A]). Ensuite, appuyez sur la touche inverse de votre calculatrice, . Cela peut nécessiter l'utilisation du 2nd bouton, en fonction de votre calculatrice. Votre écran devrait afficher . Appuyez sur Entrée et la matrice inverse doit apparaître sur votre écran.[16]
8 Utilisez la clé inverse pour trouver la matrice inverse. Tout d'abord, rouvrez la fonction Matrix et utilisez le bouton Noms pour sélectionner l'étiquette de matrice que vous avez utilisée pour définir votre matrice (probablement [A]). Ensuite, appuyez sur la touche inverse de votre calculatrice, . Cela peut nécessiter l'utilisation du 2nd bouton, en fonction de votre calculatrice. Votre écran devrait afficher . Appuyez sur Entrée et la matrice inverse doit apparaître sur votre écran.[16] - N'utilisez pas le bouton ^ de votre calculatrice pour essayer de saisir A ^ -1 en tant que frappes distinctes. La calculatrice ne comprendra pas cette opération.
- Si vous recevez un message d'erreur lorsque vous entrez la clé inverse, il est probable que votre matrice d'origine ne soit pas inversée. Vous voudrez peut-être revenir en arrière et calculer le déterminant pour le découvrir.
-
 9 Convertissez votre matrice inverse en réponses exactes. Le premier calcul que la calculatrice vous donnera est sous forme décimale. Cela n'est pas considéré comme «exact» dans la plupart des cas. Vous devez convertir les réponses décimales en forme fractionnaire, si nécessaire. (Si vous êtes très chanceux, tous vos résultats seront des entiers, mais c'est rare.)[17]
9 Convertissez votre matrice inverse en réponses exactes. Le premier calcul que la calculatrice vous donnera est sous forme décimale. Cela n'est pas considéré comme «exact» dans la plupart des cas. Vous devez convertir les réponses décimales en forme fractionnaire, si nécessaire. (Si vous êtes très chanceux, tous vos résultats seront des entiers, mais c'est rare.)[17] - Votre calculatrice a probablement une fonction qui convertira automatiquement les décimales en fractions. Par exemple, à l'aide de la TI-86, entrez la fonction Math, puis sélectionnez Misc, puis Frac et Enter. Les décimales apparaîtront automatiquement sous forme de fractions.
- 10 La plupart des calculatrices graphiques ont aussi des touches entre crochets (sur TI-84, il s'agit de 2nd + x et 2nd + -) qui peuvent être utilisées pour taper une matrice sans utiliser la fonction de matrice. Remarque: la calculatrice ne formatera pas la matrice avant que la clé enter / equals ait été utilisée (c’est-à-dire que tout sera une ligne et non jolie).
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Vérifiez le déterminant de la matrice. Vous devez calculer le déterminant de la matrice comme étape initiale. Si le déterminant est 0, votre travail est terminé car la matrice n'a pas d'inverse. Le déterminant de la matrice M peut être représenté symboliquement par det (M).[1]
1 Vérifiez le déterminant de la matrice. Vous devez calculer le déterminant de la matrice comme étape initiale. Si le déterminant est 0, votre travail est terminé car la matrice n'a pas d'inverse. Le déterminant de la matrice M peut être représenté symboliquement par det (M).[1]  2 Transposer la matrice d'origine. Transposer signifie refléter la matrice autour de la diagonale principale ou, de manière équivalente, échanger le (i, j) ème élément et le (j, i) th. Lorsque vous transposez les termes de la matrice, vous devriez voir que la diagonale principale (de gauche à droite) est inchangée.[2]
2 Transposer la matrice d'origine. Transposer signifie refléter la matrice autour de la diagonale principale ou, de manière équivalente, échanger le (i, j) ème élément et le (j, i) th. Lorsque vous transposez les termes de la matrice, vous devriez voir que la diagonale principale (de gauche à droite) est inchangée.[2]  3 Trouvez le déterminant de chacune des matrices 2x2 mineures. Chaque élément de la matrice 3x3 nouvellement transposée est associé à une matrice 2x2 correspondante «mineure». Pour trouver la matrice mineure correcte pour chaque terme, commencez par mettre en évidence la ligne et la colonne avec lesquelles vous avez commencé. Cela devrait inclure cinq termes de la matrice. Les quatre termes restants constituent la matrice mineure.[3]
3 Trouvez le déterminant de chacune des matrices 2x2 mineures. Chaque élément de la matrice 3x3 nouvellement transposée est associé à une matrice 2x2 correspondante «mineure». Pour trouver la matrice mineure correcte pour chaque terme, commencez par mettre en évidence la ligne et la colonne avec lesquelles vous avez commencé. Cela devrait inclure cinq termes de la matrice. Les quatre termes restants constituent la matrice mineure.[3] 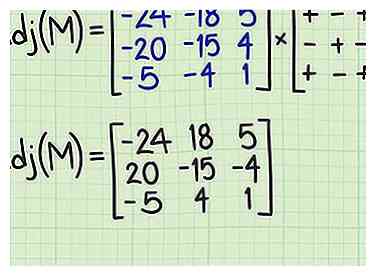 4 Créez la matrice de cofacteurs. Placer les résultats de l'étape précédente dans une nouvelle matrice de cofacteurs en alignant chaque déterminant de matrice mineur avec la position correspondante dans la matrice d'origine. Ainsi, le déterminant que vous avez calculé à partir de l'élément (1,1) de la matrice d'origine passe en position (1,1). Vous devez ensuite inverser le signe de l'alternance des termes de cette nouvelle matrice, en suivant le motif «damier» illustré.[4]
4 Créez la matrice de cofacteurs. Placer les résultats de l'étape précédente dans une nouvelle matrice de cofacteurs en alignant chaque déterminant de matrice mineur avec la position correspondante dans la matrice d'origine. Ainsi, le déterminant que vous avez calculé à partir de l'élément (1,1) de la matrice d'origine passe en position (1,1). Vous devez ensuite inverser le signe de l'alternance des termes de cette nouvelle matrice, en suivant le motif «damier» illustré.[4] 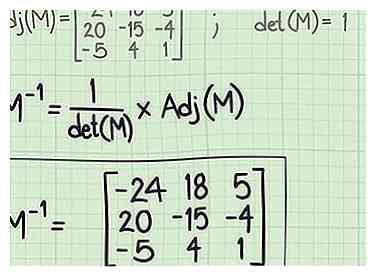 5 Diviser chaque terme de la matrice adjugate par le déterminant. Rappelez-vous le déterminant de M que vous avez calculé dans la première étape (pour vérifier que l'inverse était possible). Vous divisez maintenant chaque terme de la matrice par cette valeur. Placez le résultat de chaque calcul à l'endroit du terme d'origine. Le résultat est l'inverse de la matrice d'origine.[5]
5 Diviser chaque terme de la matrice adjugate par le déterminant. Rappelez-vous le déterminant de M que vous avez calculé dans la première étape (pour vérifier que l'inverse était possible). Vous divisez maintenant chaque terme de la matrice par cette valeur. Placez le résultat de chaque calcul à l'endroit du terme d'origine. Le résultat est l'inverse de la matrice d'origine.[5]  1 Joindre la matrice d'identité à la matrice d'origine. Écrivez la matrice originale M, tracez une ligne verticale à sa droite, puis écrivez la matrice d'identité à droite de celle-ci. Vous devriez maintenant avoir ce qui semble être une matrice de trois lignes de six colonnes chacune.[6]
1 Joindre la matrice d'identité à la matrice d'origine. Écrivez la matrice originale M, tracez une ligne verticale à sa droite, puis écrivez la matrice d'identité à droite de celle-ci. Vous devriez maintenant avoir ce qui semble être une matrice de trois lignes de six colonnes chacune.[6]  2 Effectuer des opérations de réduction de lignes linéaires. Votre objectif est de créer la matrice d'identité sur le côté gauche de cette nouvelle matrice augmentée. Au fur et à mesure que vous effectuez des étapes de réduction de ligne sur la gauche, vous devez effectuer systématiquement les mêmes opérations sur la droite, qui a commencé par votre matrice d'identité.[7]
2 Effectuer des opérations de réduction de lignes linéaires. Votre objectif est de créer la matrice d'identité sur le côté gauche de cette nouvelle matrice augmentée. Au fur et à mesure que vous effectuez des étapes de réduction de ligne sur la gauche, vous devez effectuer systématiquement les mêmes opérations sur la droite, qui a commencé par votre matrice d'identité.[7]  3 Continuez jusqu'à ce que vous formiez la matrice d'identité. Continuez à répéter les opérations de réduction des lignes linéaires jusqu'à ce que le côté gauche de votre matrice augmentée affiche la matrice d'identité (diagonale de 1s, avec les autres termes 0). Lorsque vous avez atteint ce point, le côté droit de votre séparateur vertical sera l'inverse de votre matrice d'origine.[8]
3 Continuez jusqu'à ce que vous formiez la matrice d'identité. Continuez à répéter les opérations de réduction des lignes linéaires jusqu'à ce que le côté gauche de votre matrice augmentée affiche la matrice d'identité (diagonale de 1s, avec les autres termes 0). Lorsque vous avez atteint ce point, le côté droit de votre séparateur vertical sera l'inverse de votre matrice d'origine.[8]  4 Écrivez la matrice inverse. Copiez les éléments qui apparaissent maintenant du côté droit du diviseur vertical en tant que matrice inverse.[9]
4 Écrivez la matrice inverse. Copiez les éléments qui apparaissent maintenant du côté droit du diviseur vertical en tant que matrice inverse.[9]  1 Sélectionnez une calculatrice avec des capacités de matrice. Les simples calculatrices à 4 fonctions ne pourront pas vous aider à trouver directement l'inverse. Cependant, en raison de la nature répétitive des calculs, une calculatrice graphique avancée, telle que la Texas Instruments TI-83 ou TI-86, peut considérablement réduire le travail.[10]
1 Sélectionnez une calculatrice avec des capacités de matrice. Les simples calculatrices à 4 fonctions ne pourront pas vous aider à trouver directement l'inverse. Cependant, en raison de la nature répétitive des calculs, une calculatrice graphique avancée, telle que la Texas Instruments TI-83 ou TI-86, peut considérablement réduire le travail.[10]  2 Entrez votre matrice dans la calculatrice. Tout d'abord, entrez la fonction Matrix de votre calculatrice en appuyant sur la touche Matrix, si vous en avez une. Sur les calculatrices Texas Instruments, vous devrez peut-être appuyer sur 2nd Matrice.
2 Entrez votre matrice dans la calculatrice. Tout d'abord, entrez la fonction Matrix de votre calculatrice en appuyant sur la touche Matrix, si vous en avez une. Sur les calculatrices Texas Instruments, vous devrez peut-être appuyer sur 2nd Matrice.  3 Sélectionnez le sous-menu Modifier. Pour accéder au sous-menu, vous devrez peut-être utiliser les boutons fléchés ou choisir la touche de fonction appropriée en haut du clavier de votre calculatrice, en fonction de la disposition de votre calculatrice.[11]
3 Sélectionnez le sous-menu Modifier. Pour accéder au sous-menu, vous devrez peut-être utiliser les boutons fléchés ou choisir la touche de fonction appropriée en haut du clavier de votre calculatrice, en fonction de la disposition de votre calculatrice.[11]  4 Sélectionnez un nom pour votre matrice. La plupart des calculatrices sont équipées de 3 à 10 matrices, identifiées par les lettres A à J. En règle générale, choisissez simplement [A] pour travailler. Appuyez sur la touche Entrée après avoir effectué votre sélection.[12]
4 Sélectionnez un nom pour votre matrice. La plupart des calculatrices sont équipées de 3 à 10 matrices, identifiées par les lettres A à J. En règle générale, choisissez simplement [A] pour travailler. Appuyez sur la touche Entrée après avoir effectué votre sélection.[12]  5 Entrez les dimensions de votre matrice. Cet article se concentre sur les matrices 3x3. Cependant, la calculatrice peut gérer des tailles plus grandes. Entrez le nombre de lignes, puis appuyez sur Entrée, puis sur le nombre de colonnes et sur Entrée.[13]
5 Entrez les dimensions de votre matrice. Cet article se concentre sur les matrices 3x3. Cependant, la calculatrice peut gérer des tailles plus grandes. Entrez le nombre de lignes, puis appuyez sur Entrée, puis sur le nombre de colonnes et sur Entrée.[13]  6 Entrez chaque élément de la matrice. L'écran de la calculatrice affichera une matrice. Si vous travailliez auparavant avec la fonction matrice, la matrice précédente apparaîtra à l'écran. Le curseur mettra en évidence le premier élément de la matrice. Tapez la valeur de la matrice que vous souhaitez résoudre, puis entrez. Le curseur se déplacera automatiquement vers l'élément suivant de la matrice, en écrasant tous les numéros précédents.[14]
6 Entrez chaque élément de la matrice. L'écran de la calculatrice affichera une matrice. Si vous travailliez auparavant avec la fonction matrice, la matrice précédente apparaîtra à l'écran. Le curseur mettra en évidence le premier élément de la matrice. Tapez la valeur de la matrice que vous souhaitez résoudre, puis entrez. Le curseur se déplacera automatiquement vers l'élément suivant de la matrice, en écrasant tous les numéros précédents.[14]  7 Quittez la fonction Matrix. Après avoir entré toutes les valeurs de la matrice, appuyez sur la touche Quitter (ou 2nd Quittez, si nécessaire). Cela vous quittera de la fonction Matrix et vous ramènera à l'écran d'affichage principal de votre calculatrice.[15]
7 Quittez la fonction Matrix. Après avoir entré toutes les valeurs de la matrice, appuyez sur la touche Quitter (ou 2nd Quittez, si nécessaire). Cela vous quittera de la fonction Matrix et vous ramènera à l'écran d'affichage principal de votre calculatrice.[15]  8 Utilisez la clé inverse pour trouver la matrice inverse. Tout d'abord, rouvrez la fonction Matrix et utilisez le bouton Noms pour sélectionner l'étiquette de matrice que vous avez utilisée pour définir votre matrice (probablement [A]). Ensuite, appuyez sur la touche inverse de votre calculatrice,
8 Utilisez la clé inverse pour trouver la matrice inverse. Tout d'abord, rouvrez la fonction Matrix et utilisez le bouton Noms pour sélectionner l'étiquette de matrice que vous avez utilisée pour définir votre matrice (probablement [A]). Ensuite, appuyez sur la touche inverse de votre calculatrice,  9 Convertissez votre matrice inverse en réponses exactes. Le premier calcul que la calculatrice vous donnera est sous forme décimale. Cela n'est pas considéré comme «exact» dans la plupart des cas. Vous devez convertir les réponses décimales en forme fractionnaire, si nécessaire. (Si vous êtes très chanceux, tous vos résultats seront des entiers, mais c'est rare.)[17]
9 Convertissez votre matrice inverse en réponses exactes. Le premier calcul que la calculatrice vous donnera est sous forme décimale. Cela n'est pas considéré comme «exact» dans la plupart des cas. Vous devez convertir les réponses décimales en forme fractionnaire, si nécessaire. (Si vous êtes très chanceux, tous vos résultats seront des entiers, mais c'est rare.)[17]