Les preuves mathématiques peuvent être difficiles, mais peuvent être conquises avec les connaissances de base appropriées en mathématiques et le format d'une épreuve. Malheureusement, il n'y a pas de moyen rapide et facile d'apprendre à construire une épreuve. Vous devez avoir une base de base dans le sujet pour trouver les théorèmes et les définitions appropriés pour concevoir logiquement votre preuve. En lisant des exemples de preuves et en pratiquant vous-même, vous serez en mesure de cultiver la compétence d’écrire une preuve mathématique.
Méthode One of Three:
Comprendre le problème
-
 1 Identifier la question. Vous devez d'abord déterminer exactement ce que vous essayez de prouver. Cette question servira également de déclaration finale dans la preuve. Dans cette étape, vous souhaitez également définir les hypothèses sur lesquelles vous allez travailler. Identifier la question et les hypothèses nécessaires vous donne un point de départ pour comprendre le problème et travailler la preuve.
1 Identifier la question. Vous devez d'abord déterminer exactement ce que vous essayez de prouver. Cette question servira également de déclaration finale dans la preuve. Dans cette étape, vous souhaitez également définir les hypothèses sur lesquelles vous allez travailler. Identifier la question et les hypothèses nécessaires vous donne un point de départ pour comprendre le problème et travailler la preuve. -
 2 Dessine des diagrammes. Lorsque vous essayez de comprendre le fonctionnement interne d'un problème de mathématiques, le plus simple est parfois de tracer un diagramme de ce qui se passe. Les diagrammes sont particulièrement importants dans les épreuves de géométrie, car ils vous aident à visualiser ce que vous essayez de prouver.
2 Dessine des diagrammes. Lorsque vous essayez de comprendre le fonctionnement interne d'un problème de mathématiques, le plus simple est parfois de tracer un diagramme de ce qui se passe. Les diagrammes sont particulièrement importants dans les épreuves de géométrie, car ils vous aident à visualiser ce que vous essayez de prouver. - Utilisez les informations fournies dans le problème pour dessiner un dessin de la preuve. Étiquetez les connus et les inconnus.
- Au fur et à mesure que vous travaillez sur la preuve, dessinez les informations nécessaires pour fournir la preuve de la preuve.
-
 3 Étudiez les preuves des théorèmes associés. Les épreuves sont difficiles à apprendre à écrire, mais une excellente façon d'apprendre les épreuves est d'étudier les théorèmes connexes et la façon dont ils ont été prouvés.
3 Étudiez les preuves des théorèmes associés. Les épreuves sont difficiles à apprendre à écrire, mais une excellente façon d'apprendre les épreuves est d'étudier les théorèmes connexes et la façon dont ils ont été prouvés. - Réalisez qu'une preuve est juste un bon argument à chaque étape justifiée. Vous pouvez trouver de nombreuses preuves à étudier en ligne ou dans un manuel.[1]
-
 4 Poser des questions. Il est parfaitement correct de rester coincé sur une preuve. Demandez à votre professeur ou à vos camarades de classe si vous avez des questions. Ils peuvent avoir des questions similaires et vous pouvez résoudre les problèmes ensemble. Il vaut mieux demander et obtenir des éclaircissements que de trébucher aveuglément sur la preuve.
4 Poser des questions. Il est parfaitement correct de rester coincé sur une preuve. Demandez à votre professeur ou à vos camarades de classe si vous avez des questions. Ils peuvent avoir des questions similaires et vous pouvez résoudre les problèmes ensemble. Il vaut mieux demander et obtenir des éclaircissements que de trébucher aveuglément sur la preuve. - Rencontrez votre professeur hors classe pour des instructions supplémentaires.
Méthode deux sur trois:
Formater une preuve
-
 1 Définir des preuves mathématiques. Une preuve mathématique est une série d'instructions logiques supportées par des théorèmes et des définitions qui prouvent la vérité d'un autre énoncé mathématique.[2] Les preuves sont le seul moyen de savoir qu'une déclaration est mathématiquement valide.
1 Définir des preuves mathématiques. Une preuve mathématique est une série d'instructions logiques supportées par des théorèmes et des définitions qui prouvent la vérité d'un autre énoncé mathématique.[2] Les preuves sont le seul moyen de savoir qu'une déclaration est mathématiquement valide. - Etre capable d'écrire une preuve mathématique indique une compréhension fondamentale du problème lui-même et de tous les concepts utilisés dans le problème.
- Les preuves vous obligent également à regarder les mathématiques d'une manière nouvelle et passionnante. Juste en essayant de prouver quelque chose que vous acquérez de la connaissance et de la compréhension même si votre preuve ne fonctionne finalement pas.
-
 2 Connaissez votre public Avant de rédiger une épreuve, vous devez penser au public pour lequel vous écrivez et aux informations qu’ils connaissent déjà. Si vous écrivez une preuve pour publication, vous écrirez cela différemment que d'écrire une preuve pour votre cours de mathématiques au secondaire.[3]
2 Connaissez votre public Avant de rédiger une épreuve, vous devez penser au public pour lequel vous écrivez et aux informations qu’ils connaissent déjà. Si vous écrivez une preuve pour publication, vous écrirez cela différemment que d'écrire une preuve pour votre cours de mathématiques au secondaire.[3] - Connaître votre audience vous permet d’écrire la preuve de manière à ce qu’elle soit compréhensible, compte tenu de la quantité de connaissances qu’elle possède.
-
 3 Identifiez le type de preuve que vous écrivez. Il existe différents types d’épreuves et celle que vous choisissez dépend de votre public et de la tâche à accomplir. Si vous ne savez pas quelle version utiliser, demandez conseil à votre professeur. Au lycée, vous devrez peut-être écrire votre épreuve dans un format spécifique tel qu'une épreuve formelle à deux colonnes.[4]
3 Identifiez le type de preuve que vous écrivez. Il existe différents types d’épreuves et celle que vous choisissez dépend de votre public et de la tâche à accomplir. Si vous ne savez pas quelle version utiliser, demandez conseil à votre professeur. Au lycée, vous devrez peut-être écrire votre épreuve dans un format spécifique tel qu'une épreuve formelle à deux colonnes.[4] - Une preuve à deux colonnes est une configuration qui place les données et les instructions dans une colonne et les éléments de preuve à côté dans une deuxième colonne. Ils sont très couramment utilisés en géométrie.
- Une preuve de paragraphe informelle utilise des énoncés grammaticalement corrects et moins de symboles. Aux niveaux supérieurs, vous devez toujours utiliser une preuve informelle.
-
 4 Écrivez l'épreuve à deux colonnes en tant que contour. La preuve en deux colonnes est un moyen facile d’organiser vos pensées et de réfléchir au problème. Tracez une ligne au milieu de la page et écrivez toutes les données et déclarations sur le côté gauche. Écrivez les définitions / théorèmes correspondants sur le côté droit, à côté des données qu'ils supportent.
4 Écrivez l'épreuve à deux colonnes en tant que contour. La preuve en deux colonnes est un moyen facile d’organiser vos pensées et de réfléchir au problème. Tracez une ligne au milieu de la page et écrivez toutes les données et déclarations sur le côté gauche. Écrivez les définitions / théorèmes correspondants sur le côté droit, à côté des données qu'ils supportent. - Par exemple:[5]
- L'angle A et l'angle B forment une paire linéaire. Donné.
- L'angle ABC est droit. Définition d'un angle droit.
- L'angle ABC mesure 180 °. Définition d'une ligne.
- Angle A + Angle B = Angle ABC. Postulat d'addition d'angle.
- Angle A + Angle B = 180 °. Substitution.
- Angle A supplémentaire à Angle B. Définition des angles supplémentaires.
- Q.E.D.
-
 5 Convertissez la preuve à deux colonnes en une preuve écrite informelle. En utilisant la preuve à deux colonnes comme base, écrivez la forme de paragraphe informelle de votre épreuve sans trop de symboles et d'abréviations.
5 Convertissez la preuve à deux colonnes en une preuve écrite informelle. En utilisant la preuve à deux colonnes comme base, écrivez la forme de paragraphe informelle de votre épreuve sans trop de symboles et d'abréviations. - Par exemple: Soit l'angle A et l'angle B des paires linéaires. Par hypothèse, l'angle A et l'angle B sont complémentaires. L'angle A et l'angle B forment une ligne droite car ce sont des paires linéaires. Une ligne droite est définie comme ayant une mesure d'angle de 180 °. Compte tenu de l’addition des angles, postulez les angles A et B pour former la ligne ABC. Grâce à la substitution, les angles A et B totalisent 180 °, ce sont donc des angles supplémentaires. Q.E.D.
Méthode trois sur trois:
Ecrire la preuve
-
 1 Apprenez le vocabulaire d'une preuve. Il y a certaines déclarations et phrases que vous verrez encore et encore dans une preuve mathématique. Ce sont des phrases que vous devez connaître et que vous devez utiliser correctement lorsque vous écrivez vos propres preuves.[6]
1 Apprenez le vocabulaire d'une preuve. Il y a certaines déclarations et phrases que vous verrez encore et encore dans une preuve mathématique. Ce sont des phrases que vous devez connaître et que vous devez utiliser correctement lorsque vous écrivez vos propres preuves.[6] - Les instructions «Si A, alors B» signifient que vous devez prouver chaque fois que A est vrai, B doit également être vrai.[7]
- «A si et seulement si B» signifie que vous devez prouver que A et B sont vrais et faux en même temps.Prouvez à la fois «si A, puis B» et «sinon A, alors pas B».
- "A seulement si B" est équivalent à "si A, alors B", donc il n'est pas fréquemment utilisé. Il est bon d'en être conscient si vous le voyez.
- Lorsque vous composez la preuve, évitez d'utiliser «I», mais utilisez «nous» à la place.[8]
-
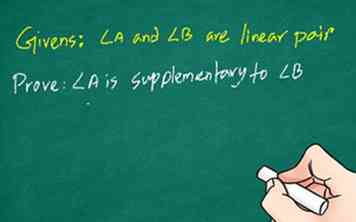 2 Notez toutes les données. Lors de la rédaction d'une épreuve, la première étape consiste à identifier et à noter toutes les données. C'est le meilleur endroit pour commencer, car il vous aide à réfléchir à ce qui est connu et aux informations dont vous aurez besoin pour compléter la preuve. Lisez le problème et écrivez chaque donnée.
2 Notez toutes les données. Lors de la rédaction d'une épreuve, la première étape consiste à identifier et à noter toutes les données. C'est le meilleur endroit pour commencer, car il vous aide à réfléchir à ce qui est connu et aux informations dont vous aurez besoin pour compléter la preuve. Lisez le problème et écrivez chaque donnée. - Par exemple: Montrer que deux angles (angle A et angle B) formant une paire linéaire sont complémentaires.[9]
- Givens: l'angle A et l'angle B sont une paire linéaire
- Prouver: l'angle A est complémentaire à l'angle B
-
 3 Définir toutes les variables. En plus d'écrire les données, il est utile de définir toutes les variables. Écrivez les définitions au début de la preuve pour éviter toute confusion pour le lecteur. Si les variables ne sont pas définies, un lecteur peut facilement se perdre en essayant de comprendre votre preuve.
3 Définir toutes les variables. En plus d'écrire les données, il est utile de définir toutes les variables. Écrivez les définitions au début de la preuve pour éviter toute confusion pour le lecteur. Si les variables ne sont pas définies, un lecteur peut facilement se perdre en essayant de comprendre votre preuve. - N'utilisez aucune variable dans votre preuve qui n'a pas été définie.
- Par exemple: Les variables sont la mesure d'angle de l'angle A et la mesure de l'angle B.
-
 4 Travaillez à travers la preuve en arrière. Il est souvent plus facile de réfléchir au problème en arrière. Commencez par la conclusion, ce que vous essayez de prouver et réfléchissez aux étapes qui peuvent vous mener au début.[10]
4 Travaillez à travers la preuve en arrière. Il est souvent plus facile de réfléchir au problème en arrière. Commencez par la conclusion, ce que vous essayez de prouver et réfléchissez aux étapes qui peuvent vous mener au début.[10] - Manipulez les étapes depuis le début et la fin pour voir si vous pouvez les faire se ressembler. Utilisez les données, les définitions que vous avez apprises et les preuves similaires à celle sur laquelle vous travaillez.
- Posez-vous des questions au fur et à mesure que vous avancez. "Pourquoi cela est-il ainsi?" et "Y a-t-il un moyen que cela puisse être faux?" sont de bonnes questions pour chaque déclaration ou revendication.
- N'oubliez pas de réécrire les étapes dans le bon ordre pour la preuve finale.
- Par exemple: si les angles A et B sont supplémentaires, ils doivent totaliser 180 °. Les deux angles se combinent pour former la ligne ABC. Vous savez qu'ils font une ligne en raison de la définition d'une paire linéaire. Comme une ligne est à 180 °, vous pouvez utiliser la substitution pour prouver que l'angle A et l'angle B totalisent 180 °.
-
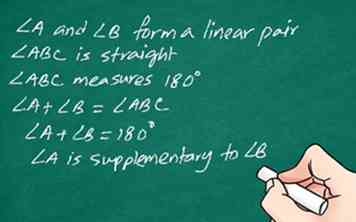 5 Commandez vos pas logiquement. Commencez la preuve au début et travaillez vers la conclusion. Bien qu'il soit utile de réfléchir à la preuve en commençant par la conclusion et en travaillant en arrière, lorsque vous écrivez la preuve, indiquez la conclusion à la fin.[11] Il doit passer d’une déclaration à l’autre, avec prise en charge de chaque déclaration, de sorte qu’il n’ya aucune raison de douter de la validité de votre preuve.
5 Commandez vos pas logiquement. Commencez la preuve au début et travaillez vers la conclusion. Bien qu'il soit utile de réfléchir à la preuve en commençant par la conclusion et en travaillant en arrière, lorsque vous écrivez la preuve, indiquez la conclusion à la fin.[11] Il doit passer d’une déclaration à l’autre, avec prise en charge de chaque déclaration, de sorte qu’il n’ya aucune raison de douter de la validité de votre preuve. - Commencez par indiquer les hypothèses avec lesquelles vous travaillez.
- Incluez des étapes simples et évidentes pour qu'un lecteur ne se demande pas comment vous êtes passés d'une étape à l'autre.
- Écrire plusieurs brouillons pour vos épreuves n'est pas rare. Continuez à réorganiser jusqu'à ce que toutes les étapes soient dans l'ordre le plus logique.
- Par exemple: Commencez par le début.
- L'angle A et l'angle B forment une paire linéaire.
- L'angle ABC est droit.
- L'angle ABC mesure 180 °.
- Angle A + Angle B = Angle ABC.
- Angle A + Angle B = Angle 180 °.
- L'angle A est complémentaire à l'angle B.
-
 6 Évitez d'utiliser des flèches et des abréviations dans la preuve écrite. Lorsque vous dessinez le plan de votre épreuve, vous pouvez utiliser un raccourci et des symboles, mais lorsque vous écrivez la preuve finale, des symboles tels que des flèches peuvent perturber le lecteur. Utilisez plutôt des mots comme «puis» ou «donc».[12]
6 Évitez d'utiliser des flèches et des abréviations dans la preuve écrite. Lorsque vous dessinez le plan de votre épreuve, vous pouvez utiliser un raccourci et des symboles, mais lorsque vous écrivez la preuve finale, des symboles tels que des flèches peuvent perturber le lecteur. Utilisez plutôt des mots comme «puis» ou «donc».[12] - Les exceptions à l'utilisation des abréviations comprennent, par ex. (par exemple) et à savoir (c'est-à-dire), mais assurez-vous de les utiliser correctement.[13]
-
 7 Soutenez toutes les déclarations avec un théorème, une loi ou une définition. Une preuve est seulement aussi bonne que la preuve utilisée. Vous ne pouvez pas faire une déclaration sans la soutenir avec une définition. Référencez d'autres preuves similaires à celle sur laquelle vous travaillez, par exemple des preuves.
7 Soutenez toutes les déclarations avec un théorème, une loi ou une définition. Une preuve est seulement aussi bonne que la preuve utilisée. Vous ne pouvez pas faire une déclaration sans la soutenir avec une définition. Référencez d'autres preuves similaires à celle sur laquelle vous travaillez, par exemple des preuves. - Essayez d'appliquer votre preuve à un cas où il devrait échouer, et voir si c'est le cas. Si cela n'échoue pas, retravaillez la preuve pour qu'elle le fasse.
- De nombreuses preuves géométriques sont écrites en tant que preuve à deux colonnes, avec la déclaration et la preuve. Une preuve mathématique formelle pour la publication est écrite en tant que paragraphe avec une grammaire correcte.
-
 8 Terminez avec une conclusion ou Q.E.D. Le dernier énoncé de la preuve devrait être le concept que vous tentiez de prouver. Une fois que vous avez fait cette déclaration, mettez fin à l'épreuve avec un dernier symbole final tel que Q.E.D. ou un carré rempli indique que la preuve est complètement terminée.[14]
8 Terminez avec une conclusion ou Q.E.D. Le dernier énoncé de la preuve devrait être le concept que vous tentiez de prouver. Une fois que vous avez fait cette déclaration, mettez fin à l'épreuve avec un dernier symbole final tel que Q.E.D. ou un carré rempli indique que la preuve est complètement terminée.[14] - Q.E.D. (quod erat demonstrandum, qui est en latin pour "qui devait être montré").
- Si vous ne savez pas si votre preuve est correcte, écrivez simplement quelques phrases indiquant votre conclusion et pourquoi elle est significative.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Identifier la question. Vous devez d'abord déterminer exactement ce que vous essayez de prouver. Cette question servira également de déclaration finale dans la preuve. Dans cette étape, vous souhaitez également définir les hypothèses sur lesquelles vous allez travailler. Identifier la question et les hypothèses nécessaires vous donne un point de départ pour comprendre le problème et travailler la preuve.
1 Identifier la question. Vous devez d'abord déterminer exactement ce que vous essayez de prouver. Cette question servira également de déclaration finale dans la preuve. Dans cette étape, vous souhaitez également définir les hypothèses sur lesquelles vous allez travailler. Identifier la question et les hypothèses nécessaires vous donne un point de départ pour comprendre le problème et travailler la preuve.  2 Dessine des diagrammes. Lorsque vous essayez de comprendre le fonctionnement interne d'un problème de mathématiques, le plus simple est parfois de tracer un diagramme de ce qui se passe. Les diagrammes sont particulièrement importants dans les épreuves de géométrie, car ils vous aident à visualiser ce que vous essayez de prouver.
2 Dessine des diagrammes. Lorsque vous essayez de comprendre le fonctionnement interne d'un problème de mathématiques, le plus simple est parfois de tracer un diagramme de ce qui se passe. Les diagrammes sont particulièrement importants dans les épreuves de géométrie, car ils vous aident à visualiser ce que vous essayez de prouver.  3 Étudiez les preuves des théorèmes associés. Les épreuves sont difficiles à apprendre à écrire, mais une excellente façon d'apprendre les épreuves est d'étudier les théorèmes connexes et la façon dont ils ont été prouvés.
3 Étudiez les preuves des théorèmes associés. Les épreuves sont difficiles à apprendre à écrire, mais une excellente façon d'apprendre les épreuves est d'étudier les théorèmes connexes et la façon dont ils ont été prouvés.  4 Poser des questions. Il est parfaitement correct de rester coincé sur une preuve. Demandez à votre professeur ou à vos camarades de classe si vous avez des questions. Ils peuvent avoir des questions similaires et vous pouvez résoudre les problèmes ensemble. Il vaut mieux demander et obtenir des éclaircissements que de trébucher aveuglément sur la preuve.
4 Poser des questions. Il est parfaitement correct de rester coincé sur une preuve. Demandez à votre professeur ou à vos camarades de classe si vous avez des questions. Ils peuvent avoir des questions similaires et vous pouvez résoudre les problèmes ensemble. Il vaut mieux demander et obtenir des éclaircissements que de trébucher aveuglément sur la preuve.  1 Définir des preuves mathématiques. Une preuve mathématique est une série d'instructions logiques supportées par des théorèmes et des définitions qui prouvent la vérité d'un autre énoncé mathématique.[2] Les preuves sont le seul moyen de savoir qu'une déclaration est mathématiquement valide.
1 Définir des preuves mathématiques. Une preuve mathématique est une série d'instructions logiques supportées par des théorèmes et des définitions qui prouvent la vérité d'un autre énoncé mathématique.[2] Les preuves sont le seul moyen de savoir qu'une déclaration est mathématiquement valide.  2 Connaissez votre public Avant de rédiger une épreuve, vous devez penser au public pour lequel vous écrivez et aux informations qu’ils connaissent déjà. Si vous écrivez une preuve pour publication, vous écrirez cela différemment que d'écrire une preuve pour votre cours de mathématiques au secondaire.[3]
2 Connaissez votre public Avant de rédiger une épreuve, vous devez penser au public pour lequel vous écrivez et aux informations qu’ils connaissent déjà. Si vous écrivez une preuve pour publication, vous écrirez cela différemment que d'écrire une preuve pour votre cours de mathématiques au secondaire.[3]  3 Identifiez le type de preuve que vous écrivez. Il existe différents types d’épreuves et celle que vous choisissez dépend de votre public et de la tâche à accomplir. Si vous ne savez pas quelle version utiliser, demandez conseil à votre professeur. Au lycée, vous devrez peut-être écrire votre épreuve dans un format spécifique tel qu'une épreuve formelle à deux colonnes.[4]
3 Identifiez le type de preuve que vous écrivez. Il existe différents types d’épreuves et celle que vous choisissez dépend de votre public et de la tâche à accomplir. Si vous ne savez pas quelle version utiliser, demandez conseil à votre professeur. Au lycée, vous devrez peut-être écrire votre épreuve dans un format spécifique tel qu'une épreuve formelle à deux colonnes.[4]  4 Écrivez l'épreuve à deux colonnes en tant que contour. La preuve en deux colonnes est un moyen facile d’organiser vos pensées et de réfléchir au problème. Tracez une ligne au milieu de la page et écrivez toutes les données et déclarations sur le côté gauche. Écrivez les définitions / théorèmes correspondants sur le côté droit, à côté des données qu'ils supportent.
4 Écrivez l'épreuve à deux colonnes en tant que contour. La preuve en deux colonnes est un moyen facile d’organiser vos pensées et de réfléchir au problème. Tracez une ligne au milieu de la page et écrivez toutes les données et déclarations sur le côté gauche. Écrivez les définitions / théorèmes correspondants sur le côté droit, à côté des données qu'ils supportent.  5 Convertissez la preuve à deux colonnes en une preuve écrite informelle. En utilisant la preuve à deux colonnes comme base, écrivez la forme de paragraphe informelle de votre épreuve sans trop de symboles et d'abréviations.
5 Convertissez la preuve à deux colonnes en une preuve écrite informelle. En utilisant la preuve à deux colonnes comme base, écrivez la forme de paragraphe informelle de votre épreuve sans trop de symboles et d'abréviations.  1 Apprenez le vocabulaire d'une preuve. Il y a certaines déclarations et phrases que vous verrez encore et encore dans une preuve mathématique. Ce sont des phrases que vous devez connaître et que vous devez utiliser correctement lorsque vous écrivez vos propres preuves.[6]
1 Apprenez le vocabulaire d'une preuve. Il y a certaines déclarations et phrases que vous verrez encore et encore dans une preuve mathématique. Ce sont des phrases que vous devez connaître et que vous devez utiliser correctement lorsque vous écrivez vos propres preuves.[6] 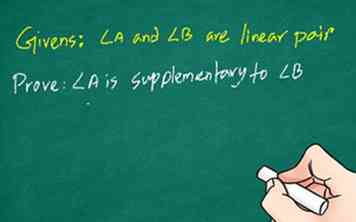 2 Notez toutes les données. Lors de la rédaction d'une épreuve, la première étape consiste à identifier et à noter toutes les données. C'est le meilleur endroit pour commencer, car il vous aide à réfléchir à ce qui est connu et aux informations dont vous aurez besoin pour compléter la preuve. Lisez le problème et écrivez chaque donnée.
2 Notez toutes les données. Lors de la rédaction d'une épreuve, la première étape consiste à identifier et à noter toutes les données. C'est le meilleur endroit pour commencer, car il vous aide à réfléchir à ce qui est connu et aux informations dont vous aurez besoin pour compléter la preuve. Lisez le problème et écrivez chaque donnée.  3 Définir toutes les variables. En plus d'écrire les données, il est utile de définir toutes les variables. Écrivez les définitions au début de la preuve pour éviter toute confusion pour le lecteur. Si les variables ne sont pas définies, un lecteur peut facilement se perdre en essayant de comprendre votre preuve.
3 Définir toutes les variables. En plus d'écrire les données, il est utile de définir toutes les variables. Écrivez les définitions au début de la preuve pour éviter toute confusion pour le lecteur. Si les variables ne sont pas définies, un lecteur peut facilement se perdre en essayant de comprendre votre preuve.  4 Travaillez à travers la preuve en arrière. Il est souvent plus facile de réfléchir au problème en arrière. Commencez par la conclusion, ce que vous essayez de prouver et réfléchissez aux étapes qui peuvent vous mener au début.[10]
4 Travaillez à travers la preuve en arrière. Il est souvent plus facile de réfléchir au problème en arrière. Commencez par la conclusion, ce que vous essayez de prouver et réfléchissez aux étapes qui peuvent vous mener au début.[10] 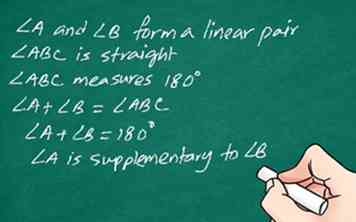 5 Commandez vos pas logiquement. Commencez la preuve au début et travaillez vers la conclusion. Bien qu'il soit utile de réfléchir à la preuve en commençant par la conclusion et en travaillant en arrière, lorsque vous écrivez la preuve, indiquez la conclusion à la fin.[11] Il doit passer d’une déclaration à l’autre, avec prise en charge de chaque déclaration, de sorte qu’il n’ya aucune raison de douter de la validité de votre preuve.
5 Commandez vos pas logiquement. Commencez la preuve au début et travaillez vers la conclusion. Bien qu'il soit utile de réfléchir à la preuve en commençant par la conclusion et en travaillant en arrière, lorsque vous écrivez la preuve, indiquez la conclusion à la fin.[11] Il doit passer d’une déclaration à l’autre, avec prise en charge de chaque déclaration, de sorte qu’il n’ya aucune raison de douter de la validité de votre preuve.  6 Évitez d'utiliser des flèches et des abréviations dans la preuve écrite. Lorsque vous dessinez le plan de votre épreuve, vous pouvez utiliser un raccourci et des symboles, mais lorsque vous écrivez la preuve finale, des symboles tels que des flèches peuvent perturber le lecteur. Utilisez plutôt des mots comme «puis» ou «donc».[12]
6 Évitez d'utiliser des flèches et des abréviations dans la preuve écrite. Lorsque vous dessinez le plan de votre épreuve, vous pouvez utiliser un raccourci et des symboles, mais lorsque vous écrivez la preuve finale, des symboles tels que des flèches peuvent perturber le lecteur. Utilisez plutôt des mots comme «puis» ou «donc».[12]  7 Soutenez toutes les déclarations avec un théorème, une loi ou une définition. Une preuve est seulement aussi bonne que la preuve utilisée. Vous ne pouvez pas faire une déclaration sans la soutenir avec une définition. Référencez d'autres preuves similaires à celle sur laquelle vous travaillez, par exemple des preuves.
7 Soutenez toutes les déclarations avec un théorème, une loi ou une définition. Une preuve est seulement aussi bonne que la preuve utilisée. Vous ne pouvez pas faire une déclaration sans la soutenir avec une définition. Référencez d'autres preuves similaires à celle sur laquelle vous travaillez, par exemple des preuves.  8 Terminez avec une conclusion ou Q.E.D. Le dernier énoncé de la preuve devrait être le concept que vous tentiez de prouver. Une fois que vous avez fait cette déclaration, mettez fin à l'épreuve avec un dernier symbole final tel que Q.E.D. ou un carré rempli indique que la preuve est complètement terminée.[14]
8 Terminez avec une conclusion ou Q.E.D. Le dernier énoncé de la preuve devrait être le concept que vous tentiez de prouver. Une fois que vous avez fait cette déclaration, mettez fin à l'épreuve avec un dernier symbole final tel que Q.E.D. ou un carré rempli indique que la preuve est complètement terminée.[14]