L'ordonnée à l'origine d'une équation est un point où le graphique de l'équation coupe l'axe des ordonnées. Il existe plusieurs façons de trouver l’interception y d’une équation, en fonction des informations de départ dont vous disposez.
Méthode One of Three:
Trouver l'interception Y à partir de la pente et du point
-
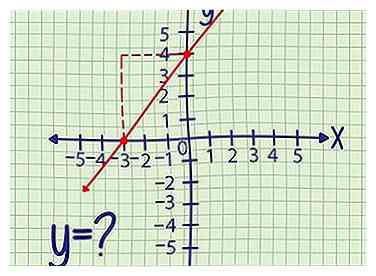 1 Notez la pente et le point. La pente ou "montée au-dessus de la ligne" est un nombre unique qui vous indique à quel point la ligne est raide. Ce type de problème vous donne également la (x, y) coordonnée d'un point le long du graphique. Passez aux autres méthodes ci-dessous si vous ne disposez pas de ces deux informations.
1 Notez la pente et le point. La pente ou "montée au-dessus de la ligne" est un nombre unique qui vous indique à quel point la ligne est raide. Ce type de problème vous donne également la (x, y) coordonnée d'un point le long du graphique. Passez aux autres méthodes ci-dessous si vous ne disposez pas de ces deux informations. - Exemple 1: Une ligne droite avec pente 2 contient le point (-3,4). Recherchez l'ordonnée à l'origine de cette ligne en suivant les étapes ci-dessous.
-
 2 Apprendre la forme d'interception de pente d'une équation. Toute ligne droite peut être écrite comme une équation dans la forme y = mx + b. Lorsque l’équation est sous cette forme, la variable m est la pente, et b est l'ordonnée à l'origine.
2 Apprendre la forme d'interception de pente d'une équation. Toute ligne droite peut être écrite comme une équation dans la forme y = mx + b. Lorsque l’équation est sous cette forme, la variable m est la pente, et b est l'ordonnée à l'origine. -
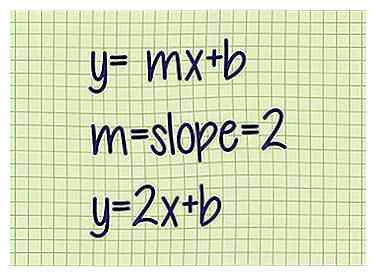 3 Remplacez la pente dans cette équation. Écrivez l’équation de pente-interception, mais au lieu de m, utilisez la pente de votre ligne.
3 Remplacez la pente dans cette équation. Écrivez l’équation de pente-interception, mais au lieu de m, utilisez la pente de votre ligne. - Exemple 1 (suite): y = mx + b
m = pente = 2
y = 2x + b
- Exemple 1 (suite): y = mx + b
-
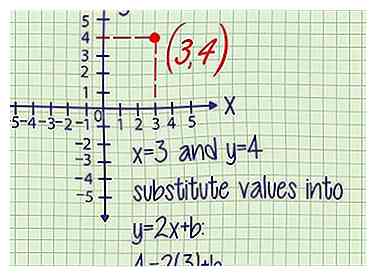 4 Remplacez x et y par les coordonnées du point. Chaque fois que vous avez les coordonnées d'un seul point sur votre ligne, vous pouvez les remplacer X et y coordonnées pour le X et y dans votre équation de ligne. Faites-le pour l'équation sur laquelle vous avez travaillé.
4 Remplacez x et y par les coordonnées du point. Chaque fois que vous avez les coordonnées d'un seul point sur votre ligne, vous pouvez les remplacer X et y coordonnées pour le X et y dans votre équation de ligne. Faites-le pour l'équation sur laquelle vous avez travaillé. - Exemple 1 (suite): Le point (3,4) est sur cette ligne. À ce point, x = 3 et y = 4.
Remplacez ces valeurs par y = 2X + b:
4 = 2(3) + b
- Exemple 1 (suite): Le point (3,4) est sur cette ligne. À ce point, x = 3 et y = 4.
-
 5 Résoudre pour b. Rappelles toi, b est l'ordonnée à l'origine de la ligne. Maintenant que b est la seule variable de l'équation, réorganiser pour résoudre cette variable et trouver la réponse.
5 Résoudre pour b. Rappelles toi, b est l'ordonnée à l'origine de la ligne. Maintenant que b est la seule variable de l'équation, réorganiser pour résoudre cette variable et trouver la réponse. - Exemple 1 (suite): 4 = 2 (3) + b
4 = 6 + b
4 - 6 = b
-2 = b
L'ordonnée à l'origine de cette ligne est -2.
- Exemple 1 (suite): 4 = 2 (3) + b
-
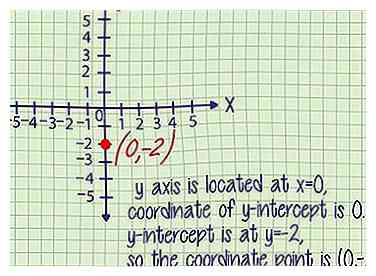 6 Ecrivez ceci comme un point de coordonnées. L'ordonnée à l'origine est le point où la ligne croise l'axe des ordonnées. Puisque l'axe des ordonnées est situé à x = 0, la coordonnée x de l'ordonnée à l'origine est toujours 0.
6 Ecrivez ceci comme un point de coordonnées. L'ordonnée à l'origine est le point où la ligne croise l'axe des ordonnées. Puisque l'axe des ordonnées est situé à x = 0, la coordonnée x de l'ordonnée à l'origine est toujours 0. - Exemple 1 (suite): L'ordonnée à l'origine est à y = -2, donc le point de coordonnées est (0, -2).
Méthode deux sur trois:
Utiliser deux points
-
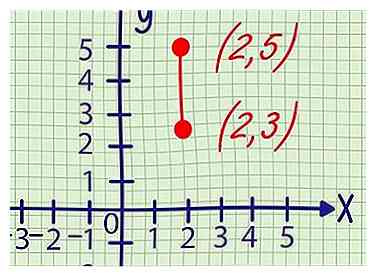 1 Notez les coordonnées des deux points. Cette méthode couvre les problèmes qui ne vous indiquent que deux points sur une ligne droite. Ecrivez chaque coordonnée de point sous la forme (x, y).
1 Notez les coordonnées des deux points. Cette méthode couvre les problèmes qui ne vous indiquent que deux points sur une ligne droite. Ecrivez chaque coordonnée de point sous la forme (x, y). -
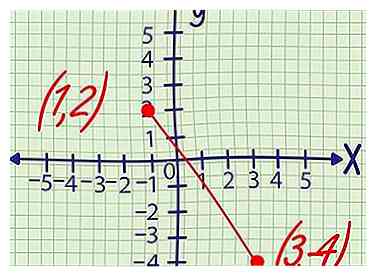 2 Exemple 2: Une ligne droite traverse des points (1, 2) et (3, -4). Recherchez l'ordonnée à l'origine de cette ligne en suivant les étapes ci-dessous.
2 Exemple 2: Une ligne droite traverse des points (1, 2) et (3, -4). Recherchez l'ordonnée à l'origine de cette ligne en suivant les étapes ci-dessous. -
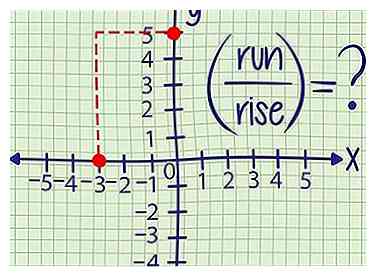 3 Calculez la montée et la course. La pente est une mesure de la distance verticale parcourue par la ligne pour chaque unité de distance horizontale. Vous avez peut-être entendu parler de "montée en puissance" (). Voici comment trouver ces deux quantités à partir de deux points:
3 Calculez la montée et la course. La pente est une mesure de la distance verticale parcourue par la ligne pour chaque unité de distance horizontale. Vous avez peut-être entendu parler de "montée en puissance" (). Voici comment trouver ces deux quantités à partir de deux points: - "Rise" est le changement de distance verticale, ou la différence entre y-valeurs des deux points.
- "Exécuter" est le changement de distance horizontale, ou la différence entre X-valeurs des deux mêmes points.
- Exemple 2 (suite): Les valeurs y des deux points sont 2 et -4, donc la hausse est (-4) - (2) = -6.
Les valeurs x des deux points (dans le même ordre) sont 1 et 3, donc le passage est 3 - 1 = 2.
-
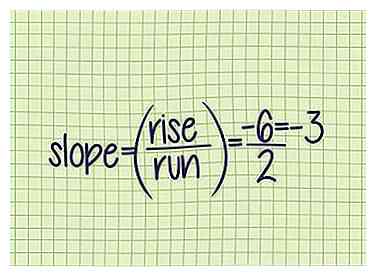 4 Diviser l'élévation pour trouver la pente. Maintenant que vous connaissez ces deux valeurs, branchez-les ""pour trouver la pente de la ligne.
4 Diviser l'élévation pour trouver la pente. Maintenant que vous connaissez ces deux valeurs, branchez-les ""pour trouver la pente de la ligne. - Exemple 2 (suite): -3.
-
 5 Examinez le formulaire d'interception de pente. Vous pouvez décrire une ligne droite avec la formule y = mx + b, où m est la pente et b est l'ordonnée à l'origine. Maintenant que nous connaissons la pente m et un point (x, y), nous pouvons utiliser cette équation pour résoudre pour b, l'ordonnée à l'origine.
5 Examinez le formulaire d'interception de pente. Vous pouvez décrire une ligne droite avec la formule y = mx + b, où m est la pente et b est l'ordonnée à l'origine. Maintenant que nous connaissons la pente m et un point (x, y), nous pouvons utiliser cette équation pour résoudre pour b, l'ordonnée à l'origine. -
 6 Ajuster la pente et pointer dans l'équation. Prendre l'équation en forme d'interception de pente et remplacer m avec la pente que vous avez calculée. Remplace le X et y termes avec les coordonnées d'un seul point sur la ligne. Peu importe quel point vous utilisez.
6 Ajuster la pente et pointer dans l'équation. Prendre l'équation en forme d'interception de pente et remplacer m avec la pente que vous avez calculée. Remplace le X et y termes avec les coordonnées d'un seul point sur la ligne. Peu importe quel point vous utilisez. - Exemple 2 (suite): y = mx + b
Slope = m = -3, donc y = -3x + b
La ligne comprend un point avec les coordonnées (x, y) (1,2), donc 2 = -3 (1) + b.
- Exemple 2 (suite): y = mx + b
-
 7 Résoudre pour b. Maintenant, la seule variable qui reste dans l'équation est b, l'ordonnée à l'origine. Réorganiser l'équation pour b est d'un côté et vous avez votre réponse. Rappelez-vous que l'ordonnée à l'origine a toujours une coordonnée x de 0.
7 Résoudre pour b. Maintenant, la seule variable qui reste dans l'équation est b, l'ordonnée à l'origine. Réorganiser l'équation pour b est d'un côté et vous avez votre réponse. Rappelez-vous que l'ordonnée à l'origine a toujours une coordonnée x de 0. - Exemple 2 (suite): 2 = -3 (1) + b
2 = -3 + b
5 = b
L'ordonnée à l'origine est à (0,5).
- Exemple 2 (suite): 2 = -3 (1) + b
Méthode trois sur trois:
Utiliser une équation
-
 1 Notez l'équation de la ligne. Si vous avez déjà l'équation de la ligne, vous pouvez trouver l'ordonnée à l'origine avec une petite algèbre.
1 Notez l'équation de la ligne. Si vous avez déjà l'équation de la ligne, vous pouvez trouver l'ordonnée à l'origine avec une petite algèbre. - Exemple 3: Quelle est l'interception y de la ligne x + 4y = 16?
- Remarque: l'exemple 3 est une ligne droite. Voir la fin de cette section pour un exemple d'équation quadratique (avec une variable portée à la puissance de 2).
-
 2 Remplacez 0 par x. L'axe des y est une ligne verticale le long de x = 0. Cela signifie que tout point sur l'axe des ordonnées a une coordonnée x de 0, y compris l'ordonnée à l'origine de la ligne.Branchez 0 pour x dans l'équation de la ligne.
2 Remplacez 0 par x. L'axe des y est une ligne verticale le long de x = 0. Cela signifie que tout point sur l'axe des ordonnées a une coordonnée x de 0, y compris l'ordonnée à l'origine de la ligne.Branchez 0 pour x dans l'équation de la ligne. - Exemple 3 (suite): x + 4y = 16
x = 0
0 + 4y = 16
4y = 16
- Exemple 3 (suite): x + 4y = 16
-
 3 Résoudre pour y. La réponse est l'interception y de la ligne.
3 Résoudre pour y. La réponse est l'interception y de la ligne. - Exemple 3 (suite): 4y = 16
y = 4.
L'ordonnée à l'origine de la ligne est 4.
- Exemple 3 (suite): 4y = 16
-
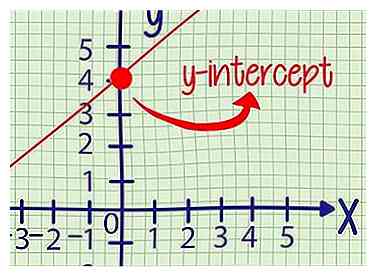 4 Confirmer par graphique (facultatif). Pour vérifier votre réponse, tracez l'équation aussi clairement que possible. Le point où la ligne croise l'axe des y est l'ordonnée à l'origine.
4 Confirmer par graphique (facultatif). Pour vérifier votre réponse, tracez l'équation aussi clairement que possible. Le point où la ligne croise l'axe des y est l'ordonnée à l'origine. -
 5 Trouver l'ordonnée à l'origine pour une équation quadratique. Une équation quadratique inclut une variable (x ou y) portée à la puissance de 2. On peut résoudre pour y avec la même substitution, mais comme le quadratique décrit une courbe, il pourrait intercepter l'axe des ordonnées à 0, 1 ou 2 points. Cela signifie que vous pouvez vous retrouver avec 0, 1 ou 2 réponses.
5 Trouver l'ordonnée à l'origine pour une équation quadratique. Une équation quadratique inclut une variable (x ou y) portée à la puissance de 2. On peut résoudre pour y avec la même substitution, mais comme le quadratique décrit une courbe, il pourrait intercepter l'axe des ordonnées à 0, 1 ou 2 points. Cela signifie que vous pouvez vous retrouver avec 0, 1 ou 2 réponses. - Exemple 4: Pour trouver l'ordonnée à l'origine de , remplacez x = 0 et résolvez l’équation quadratique.
Dans ce cas, nous pouvons résoudre en prenant la racine carrée des deux côtés. Rappelez-vous que lorsque vous prenez une racine carrée, vous devez tenir compte de deux réponses: une négative et une positive.
y = 1 ou y = -1. Ce sont deux interceptions y de cette courbe.
- Exemple 4: Pour trouver l'ordonnée à l'origine de , remplacez x = 0 et résolvez l’équation quadratique.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Notez la pente et le point. La pente ou "montée au-dessus de la ligne" est un nombre unique qui vous indique à quel point la ligne est raide. Ce type de problème vous donne également la (x, y) coordonnée d'un point le long du graphique. Passez aux autres méthodes ci-dessous si vous ne disposez pas de ces deux informations.
1 Notez la pente et le point. La pente ou "montée au-dessus de la ligne" est un nombre unique qui vous indique à quel point la ligne est raide. Ce type de problème vous donne également la (x, y) coordonnée d'un point le long du graphique. Passez aux autres méthodes ci-dessous si vous ne disposez pas de ces deux informations.  2 Apprendre la forme d'interception de pente d'une équation. Toute ligne droite peut être écrite comme une équation dans la forme y = mx + b. Lorsque l’équation est sous cette forme, la variable m est la pente, et b est l'ordonnée à l'origine.
2 Apprendre la forme d'interception de pente d'une équation. Toute ligne droite peut être écrite comme une équation dans la forme y = mx + b. Lorsque l’équation est sous cette forme, la variable m est la pente, et b est l'ordonnée à l'origine. 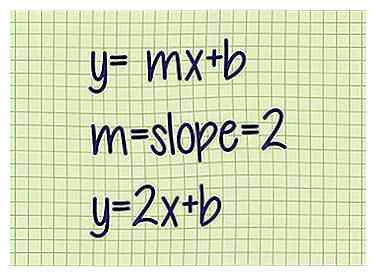 3 Remplacez la pente dans cette équation. Écrivez l’équation de pente-interception, mais au lieu de m, utilisez la pente de votre ligne.
3 Remplacez la pente dans cette équation. Écrivez l’équation de pente-interception, mais au lieu de m, utilisez la pente de votre ligne. 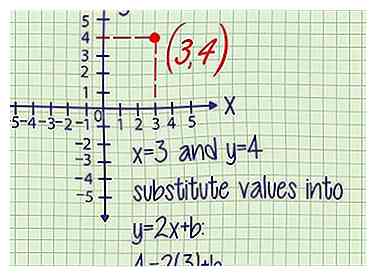 4 Remplacez x et y par les coordonnées du point. Chaque fois que vous avez les coordonnées d'un seul point sur votre ligne, vous pouvez les remplacer X et y coordonnées pour le X et y dans votre équation de ligne. Faites-le pour l'équation sur laquelle vous avez travaillé.
4 Remplacez x et y par les coordonnées du point. Chaque fois que vous avez les coordonnées d'un seul point sur votre ligne, vous pouvez les remplacer X et y coordonnées pour le X et y dans votre équation de ligne. Faites-le pour l'équation sur laquelle vous avez travaillé.  5 Résoudre pour b. Rappelles toi, b est l'ordonnée à l'origine de la ligne. Maintenant que b est la seule variable de l'équation, réorganiser pour résoudre cette variable et trouver la réponse.
5 Résoudre pour b. Rappelles toi, b est l'ordonnée à l'origine de la ligne. Maintenant que b est la seule variable de l'équation, réorganiser pour résoudre cette variable et trouver la réponse.  6 Ecrivez ceci comme un point de coordonnées. L'ordonnée à l'origine est le point où la ligne croise l'axe des ordonnées. Puisque l'axe des ordonnées est situé à x = 0, la coordonnée x de l'ordonnée à l'origine est toujours 0.
6 Ecrivez ceci comme un point de coordonnées. L'ordonnée à l'origine est le point où la ligne croise l'axe des ordonnées. Puisque l'axe des ordonnées est situé à x = 0, la coordonnée x de l'ordonnée à l'origine est toujours 0.  1 Notez les coordonnées des deux points. Cette méthode couvre les problèmes qui ne vous indiquent que deux points sur une ligne droite. Ecrivez chaque coordonnée de point sous la forme (x, y).
1 Notez les coordonnées des deux points. Cette méthode couvre les problèmes qui ne vous indiquent que deux points sur une ligne droite. Ecrivez chaque coordonnée de point sous la forme (x, y).  2 Exemple 2: Une ligne droite traverse des points (1, 2) et (3, -4). Recherchez l'ordonnée à l'origine de cette ligne en suivant les étapes ci-dessous.
2 Exemple 2: Une ligne droite traverse des points (1, 2) et (3, -4). Recherchez l'ordonnée à l'origine de cette ligne en suivant les étapes ci-dessous.  3 Calculez la montée et la course. La pente est une mesure de la distance verticale parcourue par la ligne pour chaque unité de distance horizontale. Vous avez peut-être entendu parler de "montée en puissance" (
3 Calculez la montée et la course. La pente est une mesure de la distance verticale parcourue par la ligne pour chaque unité de distance horizontale. Vous avez peut-être entendu parler de "montée en puissance" (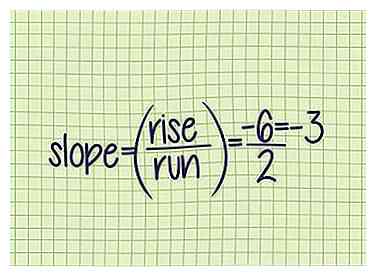 4 Diviser l'élévation pour trouver la pente. Maintenant que vous connaissez ces deux valeurs, branchez-les "
4 Diviser l'élévation pour trouver la pente. Maintenant que vous connaissez ces deux valeurs, branchez-les " 5 Examinez le formulaire d'interception de pente. Vous pouvez décrire une ligne droite avec la formule y = mx + b, où m est la pente et b est l'ordonnée à l'origine. Maintenant que nous connaissons la pente m et un point (x, y), nous pouvons utiliser cette équation pour résoudre pour b, l'ordonnée à l'origine.
5 Examinez le formulaire d'interception de pente. Vous pouvez décrire une ligne droite avec la formule y = mx + b, où m est la pente et b est l'ordonnée à l'origine. Maintenant que nous connaissons la pente m et un point (x, y), nous pouvons utiliser cette équation pour résoudre pour b, l'ordonnée à l'origine.  6 Ajuster la pente et pointer dans l'équation. Prendre l'équation en forme d'interception de pente et remplacer m avec la pente que vous avez calculée. Remplace le X et y termes avec les coordonnées d'un seul point sur la ligne. Peu importe quel point vous utilisez.
6 Ajuster la pente et pointer dans l'équation. Prendre l'équation en forme d'interception de pente et remplacer m avec la pente que vous avez calculée. Remplace le X et y termes avec les coordonnées d'un seul point sur la ligne. Peu importe quel point vous utilisez.  7 Résoudre pour b. Maintenant, la seule variable qui reste dans l'équation est b, l'ordonnée à l'origine. Réorganiser l'équation pour b est d'un côté et vous avez votre réponse. Rappelez-vous que l'ordonnée à l'origine a toujours une coordonnée x de 0.
7 Résoudre pour b. Maintenant, la seule variable qui reste dans l'équation est b, l'ordonnée à l'origine. Réorganiser l'équation pour b est d'un côté et vous avez votre réponse. Rappelez-vous que l'ordonnée à l'origine a toujours une coordonnée x de 0.  1 Notez l'équation de la ligne. Si vous avez déjà l'équation de la ligne, vous pouvez trouver l'ordonnée à l'origine avec une petite algèbre.
1 Notez l'équation de la ligne. Si vous avez déjà l'équation de la ligne, vous pouvez trouver l'ordonnée à l'origine avec une petite algèbre.  2 Remplacez 0 par x. L'axe des y est une ligne verticale le long de x = 0. Cela signifie que tout point sur l'axe des ordonnées a une coordonnée x de 0, y compris l'ordonnée à l'origine de la ligne.Branchez 0 pour x dans l'équation de la ligne.
2 Remplacez 0 par x. L'axe des y est une ligne verticale le long de x = 0. Cela signifie que tout point sur l'axe des ordonnées a une coordonnée x de 0, y compris l'ordonnée à l'origine de la ligne.Branchez 0 pour x dans l'équation de la ligne.  3 Résoudre pour y. La réponse est l'interception y de la ligne.
3 Résoudre pour y. La réponse est l'interception y de la ligne.  4 Confirmer par graphique (facultatif). Pour vérifier votre réponse, tracez l'équation aussi clairement que possible. Le point où la ligne croise l'axe des y est l'ordonnée à l'origine.
4 Confirmer par graphique (facultatif). Pour vérifier votre réponse, tracez l'équation aussi clairement que possible. Le point où la ligne croise l'axe des y est l'ordonnée à l'origine.  5 Trouver l'ordonnée à l'origine pour une équation quadratique. Une équation quadratique inclut une variable (x ou y) portée à la puissance de 2. On peut résoudre pour y avec la même substitution, mais comme le quadratique décrit une courbe, il pourrait intercepter l'axe des ordonnées à 0, 1 ou 2 points. Cela signifie que vous pouvez vous retrouver avec 0, 1 ou 2 réponses.
5 Trouver l'ordonnée à l'origine pour une équation quadratique. Une équation quadratique inclut une variable (x ou y) portée à la puissance de 2. On peut résoudre pour y avec la même substitution, mais comme le quadratique décrit une courbe, il pourrait intercepter l'axe des ordonnées à 0, 1 ou 2 points. Cela signifie que vous pouvez vous retrouver avec 0, 1 ou 2 réponses.