Le facteur d'échelle, ou facteur d'échelle linéaire, est le rapport de deux longueurs latérales correspondantes de figures similaires. Des figures similaires ont la même forme mais sont de tailles différentes. Le facteur d'échelle est utilisé pour résoudre des problèmes géométriques de base. Vous pouvez utiliser le facteur d'échelle pour trouver les longueurs latérales manquantes d'une figure. À l'inverse, vous pouvez utiliser les longueurs latérales de deux chiffres similaires pour calculer le facteur d'échelle. Ces problèmes impliquent une multiplication ou vous obligent à simplifier les fractions.
Méthode One of Four:
Trouver le facteur d'échelle de figures similaires
-
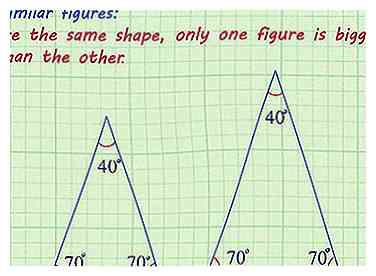 1 Vérifiez que les chiffres sont similaires. Des figures ou des formes similaires sont celles dans lesquelles les angles sont congruents et les longueurs latérales sont proportionnelles. Des figures similaires ont la même forme, une seule figure est plus grande que l'autre.[1]
1 Vérifiez que les chiffres sont similaires. Des figures ou des formes similaires sont celles dans lesquelles les angles sont congruents et les longueurs latérales sont proportionnelles. Des figures similaires ont la même forme, une seule figure est plus grande que l'autre.[1] - Le problème doit vous indiquer que les formes sont similaires ou que les angles sont identiques et indiquer que les longueurs latérales sont proportionnelles, à l’échelle ou qu’elles correspondent.
-
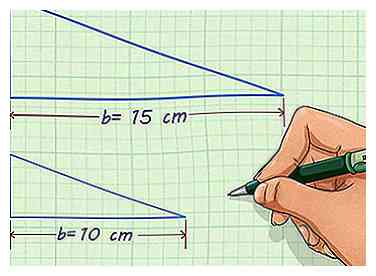 2 Trouvez une longueur de côté correspondante sur chaque figure. Vous devrez peut-être faire pivoter ou inverser la figure pour aligner les deux formes et identifier les longueurs latérales correspondantes. Il faut vous donner la longueur de ces deux côtés ou être capable de les mesurer.[2] Si vous ne connaissez pas au moins une longueur de côté de chaque figure, vous ne pouvez pas trouver le facteur d'échelle.
2 Trouvez une longueur de côté correspondante sur chaque figure. Vous devrez peut-être faire pivoter ou inverser la figure pour aligner les deux formes et identifier les longueurs latérales correspondantes. Il faut vous donner la longueur de ces deux côtés ou être capable de les mesurer.[2] Si vous ne connaissez pas au moins une longueur de côté de chaque figure, vous ne pouvez pas trouver le facteur d'échelle. - Par exemple, vous pouvez avoir un triangle avec une base de 15 cm de longueur et un triangle similaire avec une base de 10 cm de long.
-
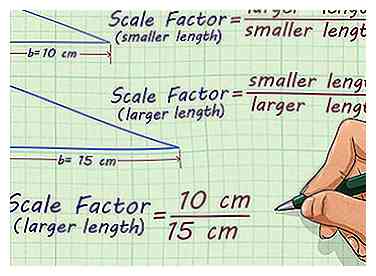 3 Mettre en place un ratio. Pour chaque paire de chiffres similaires, il existe deux facteurs d'échelle: l'un utilisé lors de la mise à l'échelle et l'autre utilisé lors de la réduction. Si vous passez d’une taille plus petite à une taille plus grande, utilisez le ratio . Si vous réduisez un plus grand chiffre à un plus petit, utilisez le ratio .[3]
3 Mettre en place un ratio. Pour chaque paire de chiffres similaires, il existe deux facteurs d'échelle: l'un utilisé lors de la mise à l'échelle et l'autre utilisé lors de la réduction. Si vous passez d’une taille plus petite à une taille plus grande, utilisez le ratio . Si vous réduisez un plus grand chiffre à un plus petit, utilisez le ratio .[3] - Par exemple, si vous réduisez un triangle avec une base de 15 cm à une base de 10 cm, vous utiliseriez le ratio .
Remplir les valeurs appropriées, cela devient .
- Par exemple, si vous réduisez un triangle avec une base de 15 cm à une base de 10 cm, vous utiliseriez le ratio .
-
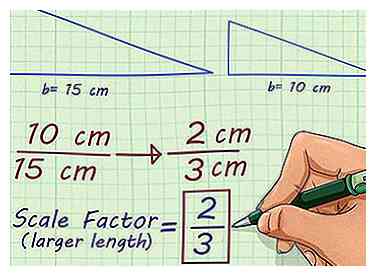 4 Simplifiez le ratio. Le ratio simplifié, ou fraction, vous donnera votre facteur d'échelle. Si vous réduisez votre échelle, votre facteur d'échelle sera une fraction appropriée.[4] Si vous augmentez, ce sera un nombre entier ou une fraction impropre, que vous pouvez convertir en un nombre décimal.
4 Simplifiez le ratio. Le ratio simplifié, ou fraction, vous donnera votre facteur d'échelle. Si vous réduisez votre échelle, votre facteur d'échelle sera une fraction appropriée.[4] Si vous augmentez, ce sera un nombre entier ou une fraction impropre, que vous pouvez convertir en un nombre décimal. - Par exemple, le ratio simplifie à . Ainsi, le facteur d'échelle de deux triangles, l'un avec une base de 15 cm et l'autre avec une base de 10 cm, est .
Méthode deux sur quatre:
Recherche d'une figure similaire à l'aide du facteur d'échelle
-
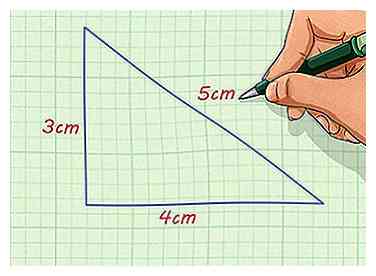 1 Trouvez les longueurs latérales de la figure. Vous devriez avoir un chiffre dont les longueurs latérales sont données ou mesurables. Si vous ne pouvez pas déterminer les longueurs latérales de la figure, vous ne pouvez pas obtenir un chiffre similaire.
1 Trouvez les longueurs latérales de la figure. Vous devriez avoir un chiffre dont les longueurs latérales sont données ou mesurables. Si vous ne pouvez pas déterminer les longueurs latérales de la figure, vous ne pouvez pas obtenir un chiffre similaire. - Par exemple, vous pouvez avoir un triangle rectangle avec des côtés mesurant 4 cm et 3 cm et une hypoténuse de 5 cm de long.
-
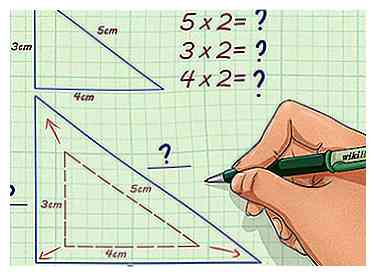 2 Déterminez si vous augmentez ou diminuez la taille. Si vous augmentez votre taille, votre chiffre manquant sera plus grand et le facteur d'échelle sera un nombre entier, une fraction impropre ou un nombre décimal. Si vous réduisez votre taille, le chiffre manquant sera plus petit et votre facteur d'échelle sera probablement une fraction appropriée.
2 Déterminez si vous augmentez ou diminuez la taille. Si vous augmentez votre taille, votre chiffre manquant sera plus grand et le facteur d'échelle sera un nombre entier, une fraction impropre ou un nombre décimal. Si vous réduisez votre taille, le chiffre manquant sera plus petit et votre facteur d'échelle sera probablement une fraction appropriée. - Par exemple, si le facteur d'échelle est 2, alors vous augmentez la taille et le chiffre similaire sera plus grand que celui que vous avez.
-
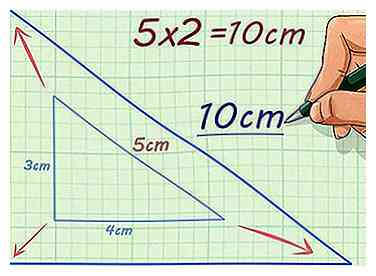 3 Multipliez la longueur d'un côté par le facteur d'échelle. Le facteur d'échelle doit vous être donné. Lorsque vous multipliez la longueur du côté par le facteur d'échelle, cela vous donne la longueur de côté correspondante manquante sur la figure similaire.[5]
3 Multipliez la longueur d'un côté par le facteur d'échelle. Le facteur d'échelle doit vous être donné. Lorsque vous multipliez la longueur du côté par le facteur d'échelle, cela vous donne la longueur de côté correspondante manquante sur la figure similaire.[5] - Par exemple, si l'hypoténuse d'un triangle rectangle a une longueur de 5 cm et que le facteur d'échelle est 2, pour calculer l'hypoténuse du triangle similaire, vous devez calculer . Donc, le triangle similaire a une hypoténuse de 10 cm de long.
-
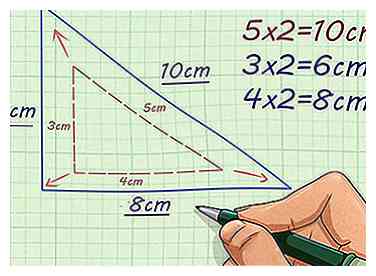 4 Trouvez les autres côtés de la figure. Continuez à multiplier chaque longueur de côté par le facteur d'échelle. Cela vous donnera les longueurs latérales correspondantes de la figure manquante.
4 Trouvez les autres côtés de la figure. Continuez à multiplier chaque longueur de côté par le facteur d'échelle. Cela vous donnera les longueurs latérales correspondantes de la figure manquante. - Par exemple, si la base d'un triangle rectangle est de 3 cm de long, avec un facteur d'échelle de 2, vous calculez pour trouver la base du triangle similaire. Si la hauteur d'un triangle rectangle est de 4 cm, avec un facteur d'échelle de 2, vous calculez pour trouver la hauteur du triangle similaire.
Méthode trois sur quatre:
Compléter les problèmes d'échantillons
-
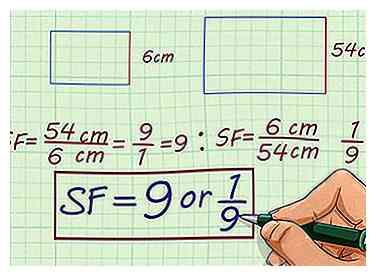 1 Trouvez le facteur d'échelle de ces chiffres similaires: un rectangle d'une hauteur de 6 cm et un rectangle d'une hauteur de 54 cm.
1 Trouvez le facteur d'échelle de ces chiffres similaires: un rectangle d'une hauteur de 6 cm et un rectangle d'une hauteur de 54 cm. - Créez un ratio en comparant les deux hauteurs. La mise à l'échelle, le ratio est . Réduire, le ratio est .
- Simplifiez le ratio. Le rapport simplifie à . Le rapport simplifie à . Les deux rectangles ont donc un facteur d'échelle de ou .
-
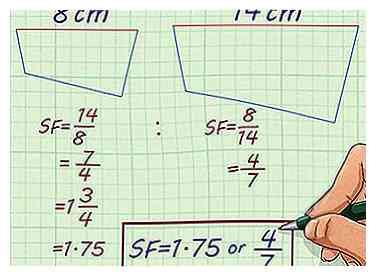 2 Essayez ce problème. Un polygone irrégulier fait 14 cm de long à son point le plus large. Un polygone irrégulier similaire est de 8 pouces à son point le plus large. Quel est le facteur d'échelle?
2 Essayez ce problème. Un polygone irrégulier fait 14 cm de long à son point le plus large. Un polygone irrégulier similaire est de 8 pouces à son point le plus large. Quel est le facteur d'échelle? - Les figures irrégulières peuvent être similaires si tous leurs côtés sont en proportion. Ainsi, vous pouvez calculer un facteur d'échelle en utilisant n'importe quelle dimension donnée.[6]
- Comme vous connaissez la largeur de chaque polygone, vous pouvez définir un ratio en les comparant. La mise à l'échelle, le ratio est . Réduire, le ratio est .
- Simplifiez le ratio. Le rapport simplifie à . Le rapport simplifie à . Les deux polygones irréguliers ont donc un facteur d'échelle de ou .
-
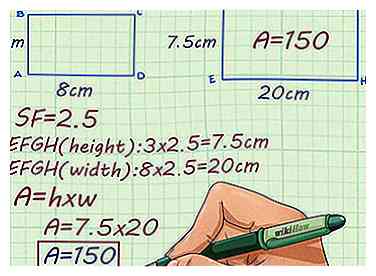 3 Utilisez le facteur d'échelle pour répondre à ce problème. Le rectangle ABCD fait 8 cm x 3 cm. Le rectangle EFGH est un rectangle plus grand et similaire. En utilisant un facteur d'échelle de 2,5, quelle est l'aire du rectangle EFGH?
3 Utilisez le facteur d'échelle pour répondre à ce problème. Le rectangle ABCD fait 8 cm x 3 cm. Le rectangle EFGH est un rectangle plus grand et similaire. En utilisant un facteur d'échelle de 2,5, quelle est l'aire du rectangle EFGH? - Multipliez la hauteur du rectangle ABCD par le facteur d'échelle. Cela vous donnera la hauteur du rectangle EFGH: .
- Multipliez la largeur du rectangle ABCD par le facteur d'échelle. Cela vous donnera la largeur du rectangle EFGH: .
- Multipliez la hauteur et la largeur du rectangle EFGH pour trouver la zone: . La surface du rectangle EFGH est donc de 150 centimètres carrés.
Méthode quatre sur quatre:
Trouver le facteur d'échelle en chimie
-
 1 Diviser la masse molaire du composé par celle de la formule empirique. Lorsque vous avez la formule empirique d'un composé chimique et que vous devez trouver la formule moléculaire de ce même composé chimique, vous pouvez trouver le facteur d'échelle dont vous avez besoin en divisant la masse molaire du composé par la masse molaire de la formule empirique.
1 Diviser la masse molaire du composé par celle de la formule empirique. Lorsque vous avez la formule empirique d'un composé chimique et que vous devez trouver la formule moléculaire de ce même composé chimique, vous pouvez trouver le facteur d'échelle dont vous avez besoin en divisant la masse molaire du composé par la masse molaire de la formule empirique. - Par exemple, vous pourriez avoir besoin de trouver la masse molaire d'un composé H2O avec une masse molaire de 54,05 g / mol.
- La masse molaire de H2O est de 18,0152 g / mol.
- Trouver le facteur d'échelle en divisant la masse molaire du composé par la masse molaire de la formule empirique:
- Facteur d'échelle = 54.05 / 18.0152 = 3
- Par exemple, vous pourriez avoir besoin de trouver la masse molaire d'un composé H2O avec une masse molaire de 54,05 g / mol.
-
 2 Multipliez la formule empirique par le facteur d'échelle. Multipliez les indices de chaque élément dans la formule empirique par le facteur d'échelle que vous venez de calculer. Cela vous donnera la formule moléculaire de l'échantillon de composé chimique impliqué dans le problème.
2 Multipliez la formule empirique par le facteur d'échelle. Multipliez les indices de chaque élément dans la formule empirique par le facteur d'échelle que vous venez de calculer. Cela vous donnera la formule moléculaire de l'échantillon de composé chimique impliqué dans le problème. - Par exemple, pour trouver la formule moléculaire du composé en question, multipliez les indices de H20 par le facteur d'échelle de 3.
- H2O * 3 = H6O3
- Par exemple, pour trouver la formule moléculaire du composé en question, multipliez les indices de H20 par le facteur d'échelle de 3.
-
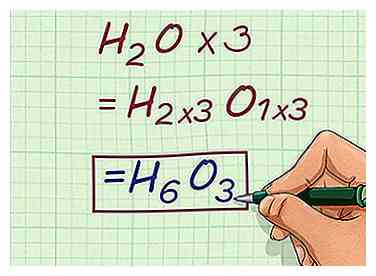 3 Écris la réponse. Avec cette réponse, vous avez trouvé la réponse à la formule empirique ainsi que la formule moléculaire du composé chimique impliqué dans le problème.
3 Écris la réponse. Avec cette réponse, vous avez trouvé la réponse à la formule empirique ainsi que la formule moléculaire du composé chimique impliqué dans le problème. - Par exemple, le facteur d'échelle pour le composé est 3. La formule moléculaire du composé est H6O3.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Vérifiez que les chiffres sont similaires. Des figures ou des formes similaires sont celles dans lesquelles les angles sont congruents et les longueurs latérales sont proportionnelles. Des figures similaires ont la même forme, une seule figure est plus grande que l'autre.[1]
1 Vérifiez que les chiffres sont similaires. Des figures ou des formes similaires sont celles dans lesquelles les angles sont congruents et les longueurs latérales sont proportionnelles. Des figures similaires ont la même forme, une seule figure est plus grande que l'autre.[1]  2 Trouvez une longueur de côté correspondante sur chaque figure. Vous devrez peut-être faire pivoter ou inverser la figure pour aligner les deux formes et identifier les longueurs latérales correspondantes. Il faut vous donner la longueur de ces deux côtés ou être capable de les mesurer.[2] Si vous ne connaissez pas au moins une longueur de côté de chaque figure, vous ne pouvez pas trouver le facteur d'échelle.
2 Trouvez une longueur de côté correspondante sur chaque figure. Vous devrez peut-être faire pivoter ou inverser la figure pour aligner les deux formes et identifier les longueurs latérales correspondantes. Il faut vous donner la longueur de ces deux côtés ou être capable de les mesurer.[2] Si vous ne connaissez pas au moins une longueur de côté de chaque figure, vous ne pouvez pas trouver le facteur d'échelle.  3 Mettre en place un ratio. Pour chaque paire de chiffres similaires, il existe deux facteurs d'échelle: l'un utilisé lors de la mise à l'échelle et l'autre utilisé lors de la réduction. Si vous passez d’une taille plus petite à une taille plus grande, utilisez le ratio
3 Mettre en place un ratio. Pour chaque paire de chiffres similaires, il existe deux facteurs d'échelle: l'un utilisé lors de la mise à l'échelle et l'autre utilisé lors de la réduction. Si vous passez d’une taille plus petite à une taille plus grande, utilisez le ratio  4 Simplifiez le ratio. Le ratio simplifié, ou fraction, vous donnera votre facteur d'échelle. Si vous réduisez votre échelle, votre facteur d'échelle sera une fraction appropriée.[4] Si vous augmentez, ce sera un nombre entier ou une fraction impropre, que vous pouvez convertir en un nombre décimal.
4 Simplifiez le ratio. Le ratio simplifié, ou fraction, vous donnera votre facteur d'échelle. Si vous réduisez votre échelle, votre facteur d'échelle sera une fraction appropriée.[4] Si vous augmentez, ce sera un nombre entier ou une fraction impropre, que vous pouvez convertir en un nombre décimal.  1 Trouvez les longueurs latérales de la figure. Vous devriez avoir un chiffre dont les longueurs latérales sont données ou mesurables. Si vous ne pouvez pas déterminer les longueurs latérales de la figure, vous ne pouvez pas obtenir un chiffre similaire.
1 Trouvez les longueurs latérales de la figure. Vous devriez avoir un chiffre dont les longueurs latérales sont données ou mesurables. Si vous ne pouvez pas déterminer les longueurs latérales de la figure, vous ne pouvez pas obtenir un chiffre similaire.  2 Déterminez si vous augmentez ou diminuez la taille. Si vous augmentez votre taille, votre chiffre manquant sera plus grand et le facteur d'échelle sera un nombre entier, une fraction impropre ou un nombre décimal. Si vous réduisez votre taille, le chiffre manquant sera plus petit et votre facteur d'échelle sera probablement une fraction appropriée.
2 Déterminez si vous augmentez ou diminuez la taille. Si vous augmentez votre taille, votre chiffre manquant sera plus grand et le facteur d'échelle sera un nombre entier, une fraction impropre ou un nombre décimal. Si vous réduisez votre taille, le chiffre manquant sera plus petit et votre facteur d'échelle sera probablement une fraction appropriée.  3 Multipliez la longueur d'un côté par le facteur d'échelle. Le facteur d'échelle doit vous être donné. Lorsque vous multipliez la longueur du côté par le facteur d'échelle, cela vous donne la longueur de côté correspondante manquante sur la figure similaire.[5]
3 Multipliez la longueur d'un côté par le facteur d'échelle. Le facteur d'échelle doit vous être donné. Lorsque vous multipliez la longueur du côté par le facteur d'échelle, cela vous donne la longueur de côté correspondante manquante sur la figure similaire.[5]  4 Trouvez les autres côtés de la figure. Continuez à multiplier chaque longueur de côté par le facteur d'échelle. Cela vous donnera les longueurs latérales correspondantes de la figure manquante.
4 Trouvez les autres côtés de la figure. Continuez à multiplier chaque longueur de côté par le facteur d'échelle. Cela vous donnera les longueurs latérales correspondantes de la figure manquante.  1 Trouvez le facteur d'échelle de ces chiffres similaires: un rectangle d'une hauteur de 6 cm et un rectangle d'une hauteur de 54 cm.
1 Trouvez le facteur d'échelle de ces chiffres similaires: un rectangle d'une hauteur de 6 cm et un rectangle d'une hauteur de 54 cm.  2 Essayez ce problème. Un polygone irrégulier fait 14 cm de long à son point le plus large. Un polygone irrégulier similaire est de 8 pouces à son point le plus large. Quel est le facteur d'échelle?
2 Essayez ce problème. Un polygone irrégulier fait 14 cm de long à son point le plus large. Un polygone irrégulier similaire est de 8 pouces à son point le plus large. Quel est le facteur d'échelle?  3 Utilisez le facteur d'échelle pour répondre à ce problème. Le rectangle ABCD fait 8 cm x 3 cm. Le rectangle EFGH est un rectangle plus grand et similaire. En utilisant un facteur d'échelle de 2,5, quelle est l'aire du rectangle EFGH?
3 Utilisez le facteur d'échelle pour répondre à ce problème. Le rectangle ABCD fait 8 cm x 3 cm. Le rectangle EFGH est un rectangle plus grand et similaire. En utilisant un facteur d'échelle de 2,5, quelle est l'aire du rectangle EFGH?  1 Diviser la masse molaire du composé par celle de la formule empirique. Lorsque vous avez la formule empirique d'un composé chimique et que vous devez trouver la formule moléculaire de ce même composé chimique, vous pouvez trouver le facteur d'échelle dont vous avez besoin en divisant la masse molaire du composé par la masse molaire de la formule empirique.
1 Diviser la masse molaire du composé par celle de la formule empirique. Lorsque vous avez la formule empirique d'un composé chimique et que vous devez trouver la formule moléculaire de ce même composé chimique, vous pouvez trouver le facteur d'échelle dont vous avez besoin en divisant la masse molaire du composé par la masse molaire de la formule empirique.  2 Multipliez la formule empirique par le facteur d'échelle. Multipliez les indices de chaque élément dans la formule empirique par le facteur d'échelle que vous venez de calculer. Cela vous donnera la formule moléculaire de l'échantillon de composé chimique impliqué dans le problème.
2 Multipliez la formule empirique par le facteur d'échelle. Multipliez les indices de chaque élément dans la formule empirique par le facteur d'échelle que vous venez de calculer. Cela vous donnera la formule moléculaire de l'échantillon de composé chimique impliqué dans le problème. 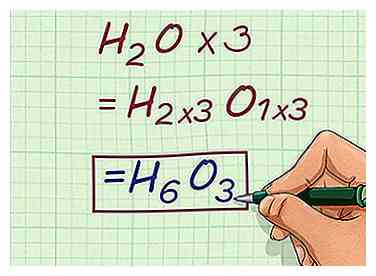 3 Écris la réponse. Avec cette réponse, vous avez trouvé la réponse à la formule empirique ainsi que la formule moléculaire du composé chimique impliqué dans le problème.
3 Écris la réponse. Avec cette réponse, vous avez trouvé la réponse à la formule empirique ainsi que la formule moléculaire du composé chimique impliqué dans le problème.