Un multiple est le résultat de la multiplication d'un nombre par un entier. Le plus petit multiple commun (LCM) d'un groupe de nombres est le plus petit nombre qui est un multiple de tous les nombres. Pour trouver le plus petit multiple commun, vous devez être en mesure d'identifier les facteurs des nombres avec lesquels vous travaillez. Vous pouvez utiliser différentes méthodes pour trouver le plus petit commun multiple. Ces méthodes fonctionnent également lors de la recherche du LCM de plus de deux nombres.
Méthode One of Four:
Liste de tous les multiples
-
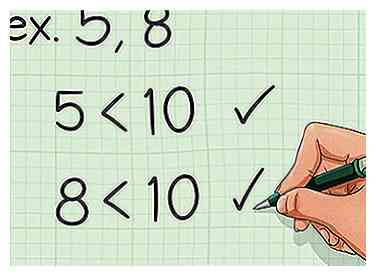 1 Evaluez vos chiffres. Cette méthode fonctionne mieux lorsque vous travaillez avec deux nombres inférieurs à 10. Si vous travaillez avec des nombres plus importants, il est préférable d'utiliser une méthode différente.
1 Evaluez vos chiffres. Cette méthode fonctionne mieux lorsque vous travaillez avec deux nombres inférieurs à 10. Si vous travaillez avec des nombres plus importants, il est préférable d'utiliser une méthode différente. - Par exemple, vous devrez peut-être trouver le plus petit multiple commun de 5 et 8. Comme il s'agit de petits nombres, il convient d'utiliser cette méthode.
-
 2 Écrivez les premiers multiples du premier nombre. Un multiple est un produit de n'importe quel nombre et d'un entier.[1] En d'autres termes, ce sont les nombres que vous verriez dans une table de multiplication.
2 Écrivez les premiers multiples du premier nombre. Un multiple est un produit de n'importe quel nombre et d'un entier.[1] En d'autres termes, ce sont les nombres que vous verriez dans une table de multiplication. - Par exemple, les premiers multiples de 5 sont 5, 10, 15, 20, 25, 30, 35 et 40.
-
 3 Écrivez les premiers multiples du deuxième nombre. Faites-le près du premier ensemble de multiples, afin qu'ils soient faciles à comparer.
3 Écrivez les premiers multiples du deuxième nombre. Faites-le près du premier ensemble de multiples, afin qu'ils soient faciles à comparer. - Par exemple, les premiers multiples de 8 sont 8, 16, 24, 32, 40, 48, 56 et 64.
-
 4 Trouvez le plus petit multiple que les nombres ont en commun. Vous devrez peut-être étendre votre liste de multiples jusqu'à ce que vous trouviez un partage des deux nombres. Ce nombre sera votre plus petit multiple commun.[2]
4 Trouvez le plus petit multiple que les nombres ont en commun. Vous devrez peut-être étendre votre liste de multiples jusqu'à ce que vous trouviez un partage des deux nombres. Ce nombre sera votre plus petit multiple commun.[2] - Par exemple, le plus petit multiple 5 et 8 est 40, donc le plus petit multiple commun de 5 et 8 est 40.
Méthode deux sur quatre:
Utilisation de la factorisation par prime
-
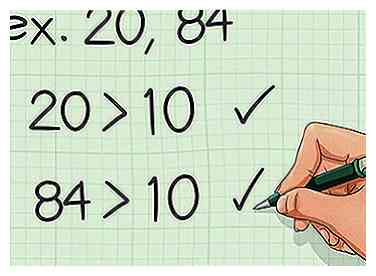 1 Evaluez vos chiffres. Cette méthode fonctionne mieux lorsque les deux nombres avec lesquels vous travaillez sont supérieurs à 10. Si vous avez des nombres plus petits, vous pouvez utiliser une méthode différente pour trouver le plus petit multiple commun plus rapidement.
1 Evaluez vos chiffres. Cette méthode fonctionne mieux lorsque les deux nombres avec lesquels vous travaillez sont supérieurs à 10. Si vous avez des nombres plus petits, vous pouvez utiliser une méthode différente pour trouver le plus petit multiple commun plus rapidement. - Par exemple, si vous devez trouver le plus petit multiple commun de 20 et 84, vous devez utiliser cette méthode.
-
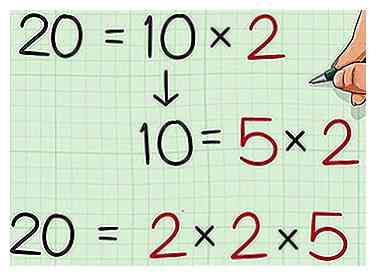 2 Facteur le premier nombre. Vous voulez factoriser le nombre en facteurs premiers; c'est à dire trouver les facteurs premiers que vous pouvez multiplier ensemble pour obtenir ce nombre. Pour ce faire, vous pouvez créer un arbre de facteurs. Une fois la factorisation terminée, réécrivez les facteurs premiers en tant qu’équation.
2 Facteur le premier nombre. Vous voulez factoriser le nombre en facteurs premiers; c'est à dire trouver les facteurs premiers que vous pouvez multiplier ensemble pour obtenir ce nombre. Pour ce faire, vous pouvez créer un arbre de facteurs. Une fois la factorisation terminée, réécrivez les facteurs premiers en tant qu’équation. - Par exemple, et , donc les facteurs premiers de 20 sont 2, 2 et 5. Réécrire comme une équation, vous obtenez .
-
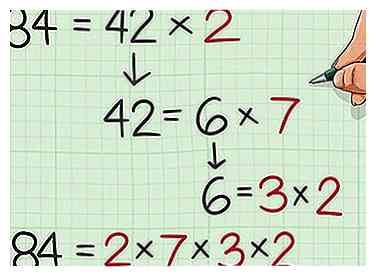 3 Facteur le deuxième nombre. Faites-le de la même manière que vous avez pris en compte le premier nombre, en trouvant les facteurs premiers que vous pouvez multiplier pour obtenir le nombre.
3 Facteur le deuxième nombre. Faites-le de la même manière que vous avez pris en compte le premier nombre, en trouvant les facteurs premiers que vous pouvez multiplier pour obtenir le nombre. - Par exemple, , , et , donc les facteurs premiers de 84 sont 2, 7, 3 et 2. Réécrire comme une équation, vous obtenez .
-
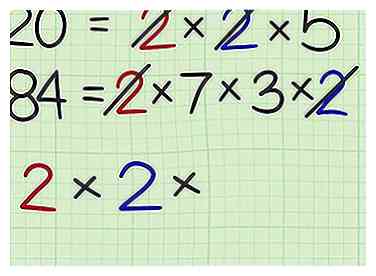 4 Notez les facteurs que chaque numéro partage. Écrivez les facteurs en tant que phrase de multiplication. Au fur et à mesure que vous écrivez chaque facteur, renseignez-le dans chaque équation de factorisation des nombres.
4 Notez les facteurs que chaque numéro partage. Écrivez les facteurs en tant que phrase de multiplication. Au fur et à mesure que vous écrivez chaque facteur, renseignez-le dans chaque équation de factorisation des nombres. - Par exemple, les deux nombres partagent un facteur de 2, alors écrivez et rayer un 2 dans l'équation de factorisation de chaque numéro.
- Chaque numéro partage également une seconde 2, changez donc la phrase de multiplication en et rayer une seconde 2 dans chaque équation de factorisation.
-
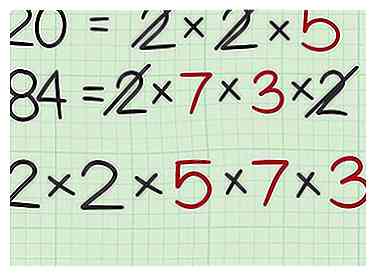 5 Ajoutez tous les facteurs restants à la phrase de multiplication. Ce sont les facteurs que vous n'avez pas rayés en comparant les deux groupes de facteurs. Ce sont donc des facteurs que les deux nombres ne partagent pas.[3]
5 Ajoutez tous les facteurs restants à la phrase de multiplication. Ce sont les facteurs que vous n'avez pas rayés en comparant les deux groupes de facteurs. Ce sont donc des facteurs que les deux nombres ne partagent pas.[3] - Par exemple, dans l'équation , vous avez barré les deux 2, car ces facteurs étaient partagés avec l’autre numéro. Vous avez un facteur de 5, ajoutez ceci à votre phrase de multiplication: .
- Dans l'équation , vous avez également barré les deux 2. Vous avez les facteurs 7 et 3 restants, alors ajoutez-les à votre phrase de multiplication: .
-
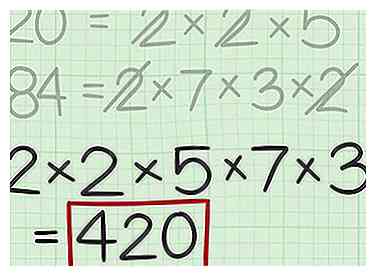 6 Calculez le plus petit multiple commun. Pour ce faire, multipliez tous les facteurs de votre phrase de multiplication.
6 Calculez le plus petit multiple commun. Pour ce faire, multipliez tous les facteurs de votre phrase de multiplication. - Par exemple, . Le plus petit multiple commun de 20 et 84 est donc 420.
Méthode trois sur quatre:
Utiliser la méthode Grid ou Ladder
-
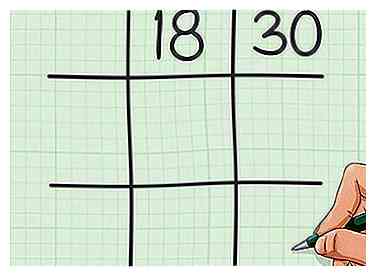 1 Dessinez une grille de tic-tac-toe. Une grille tic-tac-toe est constituée de deux ensembles de lignes parallèles qui se coupent perpendiculairement. Les lignes forment trois lignes et trois colonnes et ressemblent à la touche dièse (#) d'un téléphone ou d'un clavier. Écrivez votre premier numéro dans la case centrale supérieure de la grille. Écrivez votre deuxième numéro dans le carré en haut à droite de la grille.[4]
1 Dessinez une grille de tic-tac-toe. Une grille tic-tac-toe est constituée de deux ensembles de lignes parallèles qui se coupent perpendiculairement. Les lignes forment trois lignes et trois colonnes et ressemblent à la touche dièse (#) d'un téléphone ou d'un clavier. Écrivez votre premier numéro dans la case centrale supérieure de la grille. Écrivez votre deuxième numéro dans le carré en haut à droite de la grille.[4] - Par exemple, si vous essayez de trouver le plus petit multiple commun de 18 et 30, écrivez 18 en haut au centre de votre grille et 30 en haut à droite de votre grille.
-
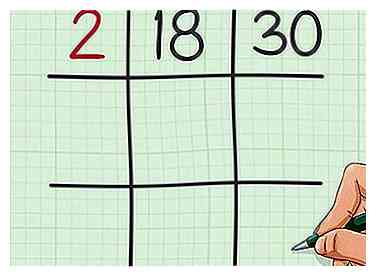 2 Recherchez un facteur commun aux deux nombres. Ecrivez ce numéro dans la case en haut à gauche de votre grille. Il est utile d'utiliser des facteurs premiers, mais vous n'êtes pas obligé de le faire.
2 Recherchez un facteur commun aux deux nombres. Ecrivez ce numéro dans la case en haut à gauche de votre grille. Il est utile d'utiliser des facteurs premiers, mais vous n'êtes pas obligé de le faire. - Par exemple, puisque 18 et 30 sont tous les deux des nombres pairs, vous savez qu’ils ont tous deux un facteur 2.Écrivez donc 2 en haut à gauche de la grille.
-
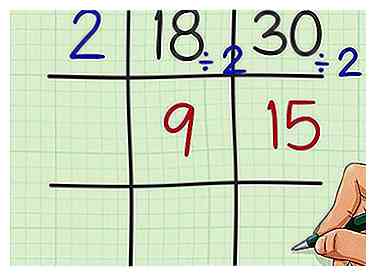 3 Diviser le facteur dans chaque nombre. Écrivez le quotient dans le carré situé en dessous de chaque chiffre. Un quotient est la réponse à un problème de division.
3 Diviser le facteur dans chaque nombre. Écrivez le quotient dans le carré situé en dessous de chaque chiffre. Un quotient est la réponse à un problème de division. - Par exemple, , écrivez donc 9 moins de 18 ans dans la grille.
- , écrivez donc 15 moins de 30 dans la grille.
-
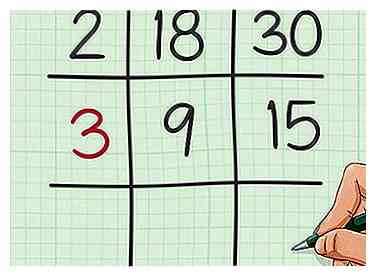 4 Trouvez un facteur commun aux deux quotients. Si aucun facteur n'est commun aux deux quotients, vous pouvez ignorer cette étape et l'étape suivante. S'il y a un facteur commun, écrivez-le dans le carré du milieu à gauche de la grille.
4 Trouvez un facteur commun aux deux quotients. Si aucun facteur n'est commun aux deux quotients, vous pouvez ignorer cette étape et l'étape suivante. S'il y a un facteur commun, écrivez-le dans le carré du milieu à gauche de la grille. - Par exemple, 9 et 15 ont tous deux un facteur de 3, vous devez donc écrire 3 au milieu à gauche de la grille.
-
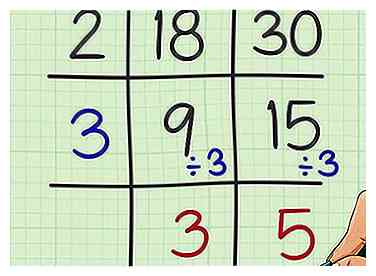 5 Diviser ce nouveau facteur dans chaque quotient. Écrivez ce nouveau quotient sous les premiers.
5 Diviser ce nouveau facteur dans chaque quotient. Écrivez ce nouveau quotient sous les premiers. - Par exemple, , écrivez donc 3 sous 9 dans la grille.
- , écrivez donc 5 moins de 15 dans la grille.
-
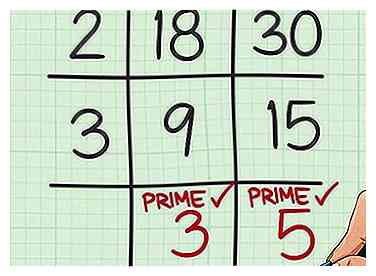 6 Étendez votre grille si nécessaire. Suivez ce même processus jusqu'à ce que le dernier ensemble de quotients n'ait pas de facteur commun.
6 Étendez votre grille si nécessaire. Suivez ce même processus jusqu'à ce que le dernier ensemble de quotients n'ait pas de facteur commun. -
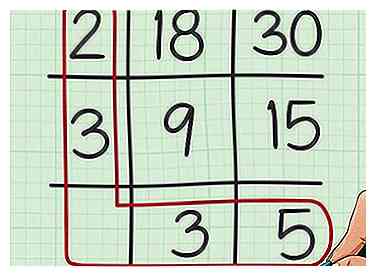 7 Tracez un cercle autour des nombres dans la première colonne et la dernière ligne de votre grille. Vous pouvez penser à dessiner un «L» pour «plus petit commun multiple». Écrivez une phrase de multiplication en utilisant tous ces facteurs.[5]
7 Tracez un cercle autour des nombres dans la première colonne et la dernière ligne de votre grille. Vous pouvez penser à dessiner un «L» pour «plus petit commun multiple». Écrivez une phrase de multiplication en utilisant tous ces facteurs.[5] - Par exemple, puisque 2 et 3 sont dans la première colonne de la grille et que 3 et 5 sont dans la dernière ligne de la grille, vous écrivez la phrase .
-
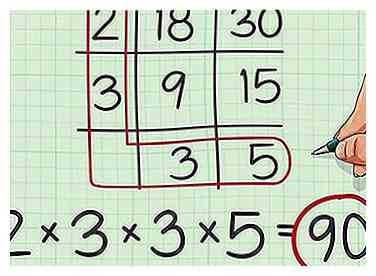 8 Terminez la multiplication. Lorsque vous multipliez tous ces facteurs ensemble, le résultat est le plus petit multiple commun de vos deux nombres originaux.[6]
8 Terminez la multiplication. Lorsque vous multipliez tous ces facteurs ensemble, le résultat est le plus petit multiple commun de vos deux nombres originaux.[6] - Par exemple, . Le plus petit multiple commun de 18 et 30 est donc 90.
Méthode quatre sur quatre:
Utiliser l'algorithme d'Euclid
-
 1 Comprendre le vocabulaire de la division. Le dividende est le nombre divisé. Le diviseur est le nombre divisé par le dividende. Le quotient est la réponse au problème de la division. Le reste est le montant qui reste après la division d’un nombre par un autre.[7]
1 Comprendre le vocabulaire de la division. Le dividende est le nombre divisé. Le diviseur est le nombre divisé par le dividende. Le quotient est la réponse au problème de la division. Le reste est le montant qui reste après la division d’un nombre par un autre.[7] - Par exemple, dans l'équation :
15 est le dividende
6 c'est le diviseur
2 est le quotient
3 est le reste.
- Par exemple, dans l'équation :
-
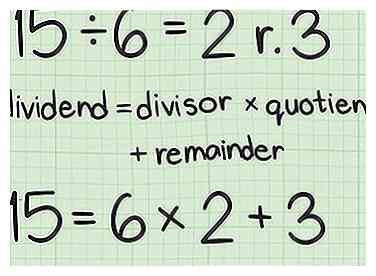 2 Configurez la formule pour le formulaire quotient-reste. La formule est .[8] Vous utiliserez ce formulaire pour configurer l'algorithme d'Euclid afin de trouver le plus grand commun diviseur de deux nombres.
2 Configurez la formule pour le formulaire quotient-reste. La formule est .[8] Vous utiliserez ce formulaire pour configurer l'algorithme d'Euclid afin de trouver le plus grand commun diviseur de deux nombres. - Par exemple, .
- Le plus grand diviseur commun est le plus grand diviseur, ou facteur, que deux nombres partagent.[9]
- Dans cette méthode, vous trouvez d'abord le plus grand diviseur commun, puis vous l'utilisez pour trouver le plus petit multiple commun.
-
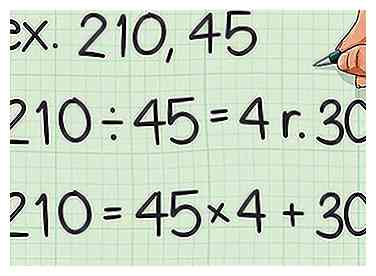 3 Utilisez le plus grand des deux nombres comme dividende. Utilisez le plus petit des deux nombres comme diviseur. Configurez une équation sous forme de quotient-reste pour ces deux nombres.
3 Utilisez le plus grand des deux nombres comme dividende. Utilisez le plus petit des deux nombres comme diviseur. Configurez une équation sous forme de quotient-reste pour ces deux nombres. - Par exemple, si vous essayez de trouver le plus petit multiple commun de 210 et 45, vous calculez .
-
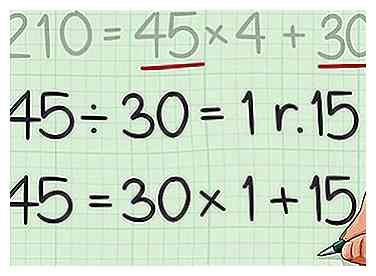 4 Utilisez le diviseur original comme nouveau dividende. Utilisez le reste comme nouveau diviseur. Configurez une équation sous forme de quotient-reste pour ces deux nombres.
4 Utilisez le diviseur original comme nouveau dividende. Utilisez le reste comme nouveau diviseur. Configurez une équation sous forme de quotient-reste pour ces deux nombres. - Par exemple, .
-
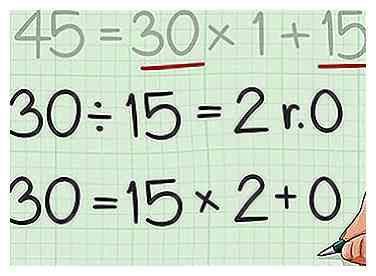 5 Répétez ce processus jusqu'à ce que vous ayez un reste de 0. Pour chaque nouvelle équation, utilisez le diviseur de l'équation précédente comme nouveau dividende et le précédent comme nouveau diviseur.[10]
5 Répétez ce processus jusqu'à ce que vous ayez un reste de 0. Pour chaque nouvelle équation, utilisez le diviseur de l'équation précédente comme nouveau dividende et le précédent comme nouveau diviseur.[10] - Par exemple, . Puisque le reste est 0, vous n'avez pas besoin de diviser davantage.
-
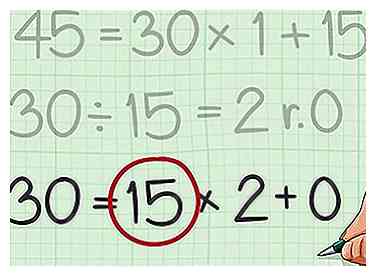 6 Regardez le dernier diviseur que vous avez utilisé. C'est le plus grand commun diviseur pour les deux nombres.[11]
6 Regardez le dernier diviseur que vous avez utilisé. C'est le plus grand commun diviseur pour les deux nombres.[11] - Par exemple, depuis la dernière équation , le dernier diviseur était 15, donc 15 est le plus grand diviseur commun de 210 et 45.
-
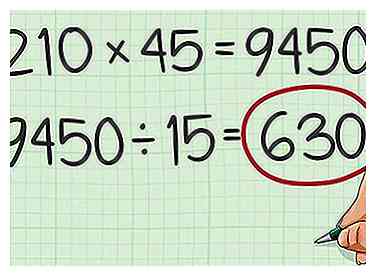 7 Multipliez les deux nombres. Diviser le produit par le plus grand commun diviseur. Cela vous donnera le plus petit multiple commun des deux nombres.[12]
7 Multipliez les deux nombres. Diviser le produit par le plus grand commun diviseur. Cela vous donnera le plus petit multiple commun des deux nombres.[12] - Par exemple, . Diviser par le plus grand diviseur commun, vous obtenez . Donc, 630 est le plus petit multiple commun de 210 et 45.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
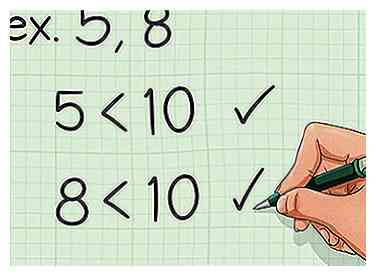 1 Evaluez vos chiffres. Cette méthode fonctionne mieux lorsque vous travaillez avec deux nombres inférieurs à 10. Si vous travaillez avec des nombres plus importants, il est préférable d'utiliser une méthode différente.
1 Evaluez vos chiffres. Cette méthode fonctionne mieux lorsque vous travaillez avec deux nombres inférieurs à 10. Si vous travaillez avec des nombres plus importants, il est préférable d'utiliser une méthode différente.  2 Écrivez les premiers multiples du premier nombre. Un multiple est un produit de n'importe quel nombre et d'un entier.[1] En d'autres termes, ce sont les nombres que vous verriez dans une table de multiplication.
2 Écrivez les premiers multiples du premier nombre. Un multiple est un produit de n'importe quel nombre et d'un entier.[1] En d'autres termes, ce sont les nombres que vous verriez dans une table de multiplication.  3 Écrivez les premiers multiples du deuxième nombre. Faites-le près du premier ensemble de multiples, afin qu'ils soient faciles à comparer.
3 Écrivez les premiers multiples du deuxième nombre. Faites-le près du premier ensemble de multiples, afin qu'ils soient faciles à comparer.  4 Trouvez le plus petit multiple que les nombres ont en commun. Vous devrez peut-être étendre votre liste de multiples jusqu'à ce que vous trouviez un partage des deux nombres. Ce nombre sera votre plus petit multiple commun.[2]
4 Trouvez le plus petit multiple que les nombres ont en commun. Vous devrez peut-être étendre votre liste de multiples jusqu'à ce que vous trouviez un partage des deux nombres. Ce nombre sera votre plus petit multiple commun.[2] 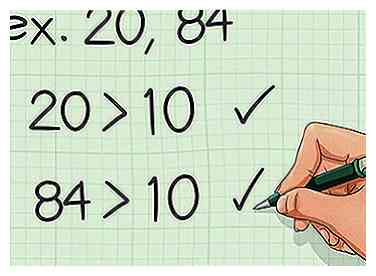 1 Evaluez vos chiffres. Cette méthode fonctionne mieux lorsque les deux nombres avec lesquels vous travaillez sont supérieurs à 10. Si vous avez des nombres plus petits, vous pouvez utiliser une méthode différente pour trouver le plus petit multiple commun plus rapidement.
1 Evaluez vos chiffres. Cette méthode fonctionne mieux lorsque les deux nombres avec lesquels vous travaillez sont supérieurs à 10. Si vous avez des nombres plus petits, vous pouvez utiliser une méthode différente pour trouver le plus petit multiple commun plus rapidement. 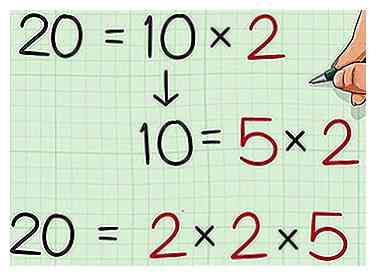 2 Facteur le premier nombre. Vous voulez factoriser le nombre en facteurs premiers; c'est à dire trouver les facteurs premiers que vous pouvez multiplier ensemble pour obtenir ce nombre. Pour ce faire, vous pouvez créer un arbre de facteurs. Une fois la factorisation terminée, réécrivez les facteurs premiers en tant qu’équation.
2 Facteur le premier nombre. Vous voulez factoriser le nombre en facteurs premiers; c'est à dire trouver les facteurs premiers que vous pouvez multiplier ensemble pour obtenir ce nombre. Pour ce faire, vous pouvez créer un arbre de facteurs. Une fois la factorisation terminée, réécrivez les facteurs premiers en tant qu’équation. 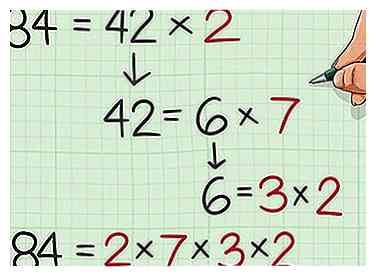 3 Facteur le deuxième nombre. Faites-le de la même manière que vous avez pris en compte le premier nombre, en trouvant les facteurs premiers que vous pouvez multiplier pour obtenir le nombre.
3 Facteur le deuxième nombre. Faites-le de la même manière que vous avez pris en compte le premier nombre, en trouvant les facteurs premiers que vous pouvez multiplier pour obtenir le nombre. 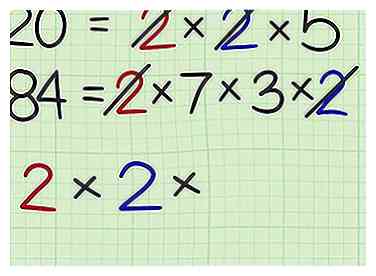 4 Notez les facteurs que chaque numéro partage. Écrivez les facteurs en tant que phrase de multiplication. Au fur et à mesure que vous écrivez chaque facteur, renseignez-le dans chaque équation de factorisation des nombres.
4 Notez les facteurs que chaque numéro partage. Écrivez les facteurs en tant que phrase de multiplication. Au fur et à mesure que vous écrivez chaque facteur, renseignez-le dans chaque équation de factorisation des nombres. 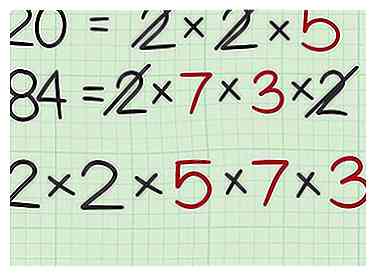 5 Ajoutez tous les facteurs restants à la phrase de multiplication. Ce sont les facteurs que vous n'avez pas rayés en comparant les deux groupes de facteurs. Ce sont donc des facteurs que les deux nombres ne partagent pas.[3]
5 Ajoutez tous les facteurs restants à la phrase de multiplication. Ce sont les facteurs que vous n'avez pas rayés en comparant les deux groupes de facteurs. Ce sont donc des facteurs que les deux nombres ne partagent pas.[3] 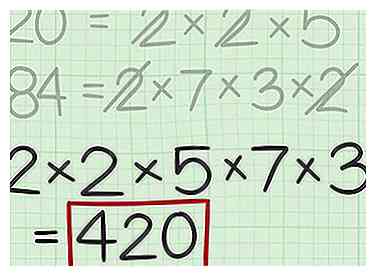 6 Calculez le plus petit multiple commun. Pour ce faire, multipliez tous les facteurs de votre phrase de multiplication.
6 Calculez le plus petit multiple commun. Pour ce faire, multipliez tous les facteurs de votre phrase de multiplication.  1 Dessinez une grille de tic-tac-toe. Une grille tic-tac-toe est constituée de deux ensembles de lignes parallèles qui se coupent perpendiculairement. Les lignes forment trois lignes et trois colonnes et ressemblent à la touche dièse (#) d'un téléphone ou d'un clavier. Écrivez votre premier numéro dans la case centrale supérieure de la grille. Écrivez votre deuxième numéro dans le carré en haut à droite de la grille.[4]
1 Dessinez une grille de tic-tac-toe. Une grille tic-tac-toe est constituée de deux ensembles de lignes parallèles qui se coupent perpendiculairement. Les lignes forment trois lignes et trois colonnes et ressemblent à la touche dièse (#) d'un téléphone ou d'un clavier. Écrivez votre premier numéro dans la case centrale supérieure de la grille. Écrivez votre deuxième numéro dans le carré en haut à droite de la grille.[4]  2 Recherchez un facteur commun aux deux nombres. Ecrivez ce numéro dans la case en haut à gauche de votre grille. Il est utile d'utiliser des facteurs premiers, mais vous n'êtes pas obligé de le faire.
2 Recherchez un facteur commun aux deux nombres. Ecrivez ce numéro dans la case en haut à gauche de votre grille. Il est utile d'utiliser des facteurs premiers, mais vous n'êtes pas obligé de le faire.  3 Diviser le facteur dans chaque nombre. Écrivez le quotient dans le carré situé en dessous de chaque chiffre. Un quotient est la réponse à un problème de division.
3 Diviser le facteur dans chaque nombre. Écrivez le quotient dans le carré situé en dessous de chaque chiffre. Un quotient est la réponse à un problème de division.  4 Trouvez un facteur commun aux deux quotients. Si aucun facteur n'est commun aux deux quotients, vous pouvez ignorer cette étape et l'étape suivante. S'il y a un facteur commun, écrivez-le dans le carré du milieu à gauche de la grille.
4 Trouvez un facteur commun aux deux quotients. Si aucun facteur n'est commun aux deux quotients, vous pouvez ignorer cette étape et l'étape suivante. S'il y a un facteur commun, écrivez-le dans le carré du milieu à gauche de la grille.  5 Diviser ce nouveau facteur dans chaque quotient. Écrivez ce nouveau quotient sous les premiers.
5 Diviser ce nouveau facteur dans chaque quotient. Écrivez ce nouveau quotient sous les premiers.  6 Étendez votre grille si nécessaire. Suivez ce même processus jusqu'à ce que le dernier ensemble de quotients n'ait pas de facteur commun.
6 Étendez votre grille si nécessaire. Suivez ce même processus jusqu'à ce que le dernier ensemble de quotients n'ait pas de facteur commun.  7 Tracez un cercle autour des nombres dans la première colonne et la dernière ligne de votre grille. Vous pouvez penser à dessiner un «L» pour «plus petit commun multiple». Écrivez une phrase de multiplication en utilisant tous ces facteurs.[5]
7 Tracez un cercle autour des nombres dans la première colonne et la dernière ligne de votre grille. Vous pouvez penser à dessiner un «L» pour «plus petit commun multiple». Écrivez une phrase de multiplication en utilisant tous ces facteurs.[5] 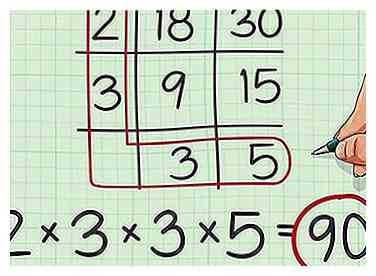 8 Terminez la multiplication. Lorsque vous multipliez tous ces facteurs ensemble, le résultat est le plus petit multiple commun de vos deux nombres originaux.[6]
8 Terminez la multiplication. Lorsque vous multipliez tous ces facteurs ensemble, le résultat est le plus petit multiple commun de vos deux nombres originaux.[6]  1 Comprendre le vocabulaire de la division. Le dividende est le nombre divisé. Le diviseur est le nombre divisé par le dividende. Le quotient est la réponse au problème de la division. Le reste est le montant qui reste après la division d’un nombre par un autre.[7]
1 Comprendre le vocabulaire de la division. Le dividende est le nombre divisé. Le diviseur est le nombre divisé par le dividende. Le quotient est la réponse au problème de la division. Le reste est le montant qui reste après la division d’un nombre par un autre.[7] 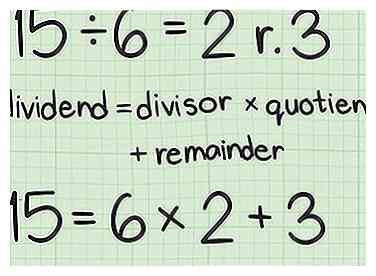 2 Configurez la formule pour le formulaire quotient-reste. La formule est
2 Configurez la formule pour le formulaire quotient-reste. La formule est 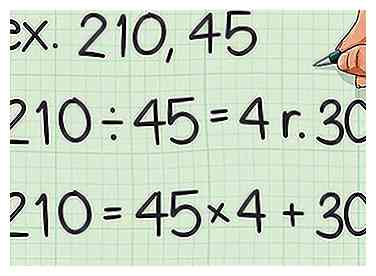 3 Utilisez le plus grand des deux nombres comme dividende. Utilisez le plus petit des deux nombres comme diviseur. Configurez une équation sous forme de quotient-reste pour ces deux nombres.
3 Utilisez le plus grand des deux nombres comme dividende. Utilisez le plus petit des deux nombres comme diviseur. Configurez une équation sous forme de quotient-reste pour ces deux nombres. 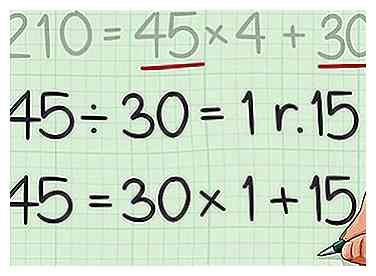 4 Utilisez le diviseur original comme nouveau dividende. Utilisez le reste comme nouveau diviseur. Configurez une équation sous forme de quotient-reste pour ces deux nombres.
4 Utilisez le diviseur original comme nouveau dividende. Utilisez le reste comme nouveau diviseur. Configurez une équation sous forme de quotient-reste pour ces deux nombres. 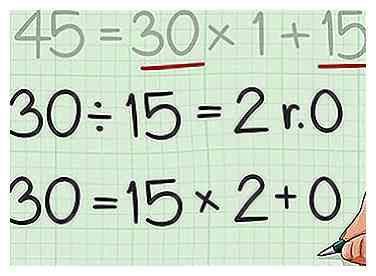 5 Répétez ce processus jusqu'à ce que vous ayez un reste de 0. Pour chaque nouvelle équation, utilisez le diviseur de l'équation précédente comme nouveau dividende et le précédent comme nouveau diviseur.[10]
5 Répétez ce processus jusqu'à ce que vous ayez un reste de 0. Pour chaque nouvelle équation, utilisez le diviseur de l'équation précédente comme nouveau dividende et le précédent comme nouveau diviseur.[10] 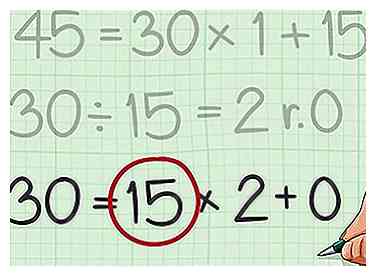 6 Regardez le dernier diviseur que vous avez utilisé. C'est le plus grand commun diviseur pour les deux nombres.[11]
6 Regardez le dernier diviseur que vous avez utilisé. C'est le plus grand commun diviseur pour les deux nombres.[11] 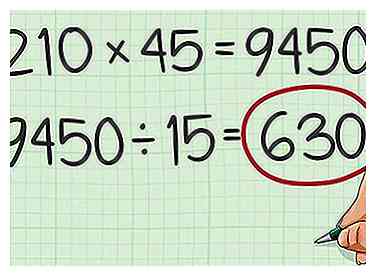 7 Multipliez les deux nombres. Diviser le produit par le plus grand commun diviseur. Cela vous donnera le plus petit multiple commun des deux nombres.[12]
7 Multipliez les deux nombres. Diviser le produit par le plus grand commun diviseur. Cela vous donnera le plus petit multiple commun des deux nombres.[12]