Lorsque deux variables sont directement proportionnelles, elles changent au même rythme. Le taux est indiqué par la constante dans l'équation . Les variables directement proportionnelles sont indiquées graphiquement par une ligne droite passant par l'origine du plan de coordonnées. Une fois que vous avez compris ces concepts de base, il est facile d'identifier les variables directement proportionnelles en utilisant l'équation de leur ligne ou leurs valeurs.
Méthode One of Four:
Réécrire l'équation de la ligne
-
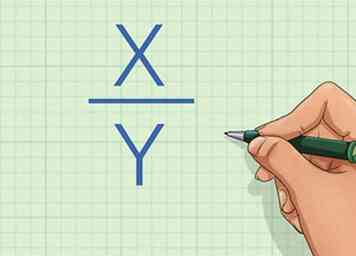 1 Comprendre la proportion directe. Deux variables sont en proportion directe si chaque variable change au même rythme.[1] En d'autres termes, si changements par un certain facteur ou une constante (), puis changements par cette même constante ().
1 Comprendre la proportion directe. Deux variables sont en proportion directe si chaque variable change au même rythme.[1] En d'autres termes, si changements par un certain facteur ou une constante (), puis changements par cette même constante (). -
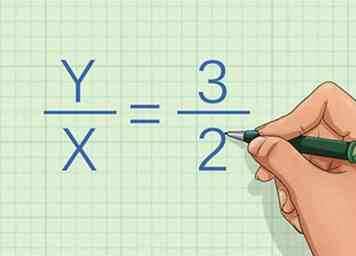 2 Notez l'équation de la ligne. L'équation aura deux variables et une constante. Si vous ne recevez pas l'équation, vous ne pouvez pas utiliser cette méthode.
2 Notez l'équation de la ligne. L'équation aura deux variables et une constante. Si vous ne recevez pas l'équation, vous ne pouvez pas utiliser cette méthode. - Par exemple, vous pourriez recevoir l'équation .
-
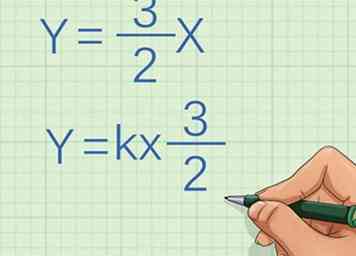 3 Réécrivez l'équation sous forme de proportion directe ou de variation. L'équation est , où est égal à la coordonnée y d'un point sur la ligne, est égal à la coordonnée x pour ce même point, et est la constante ou la pente de la ligne. Utiliser l'algèbre pour réorganiser l'équation sous la forme de . Si vous ne pouvez pas réécrire l'équation sous cette forme, les variables ne sont pas directement proportionnelles. Si vous le pouvez, cela prouve qu'ils sont directement proportionnels.[2]
3 Réécrivez l'équation sous forme de proportion directe ou de variation. L'équation est , où est égal à la coordonnée y d'un point sur la ligne, est égal à la coordonnée x pour ce même point, et est la constante ou la pente de la ligne. Utiliser l'algèbre pour réorganiser l'équation sous la forme de . Si vous ne pouvez pas réécrire l'équation sous cette forme, les variables ne sont pas directement proportionnelles. Si vous le pouvez, cela prouve qu'ils sont directement proportionnels.[2] - Par exemple, si vous multipliez les deux côtés de l'équation par , l'équation devient , qui se présente sous la forme de , avec être la constante.
Méthode deux sur quatre:
Utiliser un ensemble de points
-
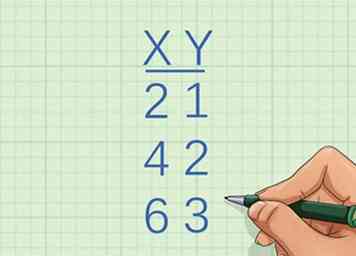 1 Identifiez les coordonnées x des deux premiers points. Vous devriez recevoir une liste de coordonnées ou avoir un graphique à partir duquel vous pouvez déterminer les coordonnées des points. Si vous n'avez pas les coordonnées des points sur la ligne, vous ne pouvez pas utiliser cette méthode.
1 Identifiez les coordonnées x des deux premiers points. Vous devriez recevoir une liste de coordonnées ou avoir un graphique à partir duquel vous pouvez déterminer les coordonnées des points. Si vous n'avez pas les coordonnées des points sur la ligne, vous ne pouvez pas utiliser cette méthode. - Par exemple, vous pourriez recevoir le jeu de points
- La coordonnée x du premier point est 2 et la coordonnée x du deuxième point est 4.
-
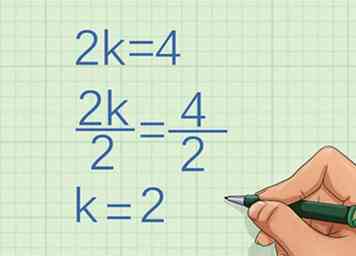 2 Déterminer le facteur par lequel le la variable augmente. Pour ce faire, déterminez quel facteur, ou constante, la première coordonnée x est multipliée par pour arriver à la deuxième coordonnée.
2 Déterminer le facteur par lequel le la variable augmente. Pour ce faire, déterminez quel facteur, ou constante, la première coordonnée x est multipliée par pour arriver à la deuxième coordonnée. - Par exemple, si la première coordonnée x est 2 et la deuxième coordonnée x 4, vous devez déterminer ce que vous multipliez par 2 pour obtenir 4:
Alors le la variable augmente de la constante 2.
- Par exemple, si la première coordonnée x est 2 et la deuxième coordonnée x 4, vous devez déterminer ce que vous multipliez par 2 pour obtenir 4:
-
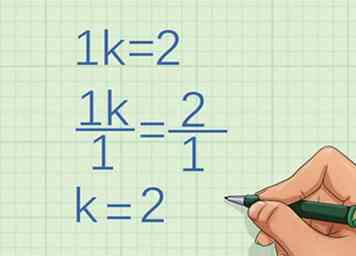 3 Déterminer le facteur par lequel le la variable augmente. Utilisez les deux mêmes points que vous avez utilisés pour déterminer la croissance de . Utilisez l'algèbre pour déterminer le facteur par lequel les deux coordonnées varient.
3 Déterminer le facteur par lequel le la variable augmente. Utilisez les deux mêmes points que vous avez utilisés pour déterminer la croissance de . Utilisez l'algèbre pour déterminer le facteur par lequel les deux coordonnées varient. - Par exemple, si la première coordonnée y est 1 et que la deuxième coordonnée y est 2, vous devez déterminer ce que vous multipliez 1 pour obtenir 2:
Donc, la variable grandit par la constante 2.
- Par exemple, si la première coordonnée y est 1 et que la deuxième coordonnée y est 2, vous devez déterminer ce que vous multipliez 1 pour obtenir 2:
-
 4 Comparez les constantes des deux variables. Si et modifiés au même rythme, ou par le même facteur, ils sont alors directement proportionnels.[3]
4 Comparez les constantes des deux variables. Si et modifiés au même rythme, ou par le même facteur, ils sont alors directement proportionnels.[3] - Par exemple, les coordonnées x ayant été modifiées d'un facteur 2, alors que les coordonnées y ont également été modifiées d'un facteur 2, les deux variables sont directement proportionnelles.
Méthode trois sur quatre:
Utiliser un graphique
-
 1 Notez si la ligne est droite. Lorsque deux variables sont en proportion, la ligne les représentant sera droite.[4] Cela signifie que la pente de la ligne est constante ou suit l’équation .
1 Notez si la ligne est droite. Lorsque deux variables sont en proportion, la ligne les représentant sera droite.[4] Cela signifie que la pente de la ligne est constante ou suit l’équation . -
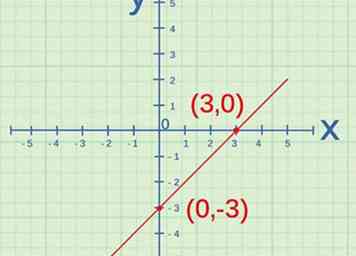 2 Détermine l'ordonnée à l'origine. L'ordonnée à l'origine est le point où la ligne traverse l'axe des y. Lorsque deux variables sont directement proportionnelles, lorsqu'elles sont représentées graphiquement, leur ligne traverse l'origine. L'origine est au point , donc l'interception y de la ligne devrait être . Si ce n'est pas le cas, les variables ne sont pas directement proportionnelles.[5]
2 Détermine l'ordonnée à l'origine. L'ordonnée à l'origine est le point où la ligne traverse l'axe des y. Lorsque deux variables sont directement proportionnelles, lorsqu'elles sont représentées graphiquement, leur ligne traverse l'origine. L'origine est au point , donc l'interception y de la ligne devrait être . Si ce n'est pas le cas, les variables ne sont pas directement proportionnelles.[5] - L'axe des y est l'axe vertical.
-
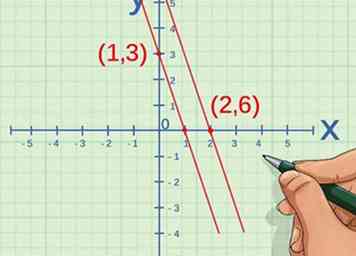 3 Trouvez les coordonnées de deux points sur la ligne. Comparez les coordonnées entre elles et déterminez si chaque coordonnée a changé du même facteur.[6] C'est-à-dire, déterminer si la constante () est la même pour les deux et valeurs.
3 Trouvez les coordonnées de deux points sur la ligne. Comparez les coordonnées entre elles et déterminez si chaque coordonnée a changé du même facteur.[6] C'est-à-dire, déterminer si la constante () est la même pour les deux et valeurs. - Par exemple, si le premier point est , et le deuxième point est , la coordonnée x changée par un facteur de 2, car . La coordonnée y a également changé d'un facteur 2, car . Ainsi, vous pouvez confirmer que la ligne représente deux variables directement proportionnelles.
Méthode quatre sur quatre:
Compléter les problèmes d'échantillons
-
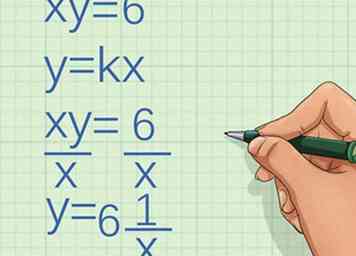 1 Regardez l'équation. Déterminer si les deux variables sont directement proportionnelles: .
1 Regardez l'équation. Déterminer si les deux variables sont directement proportionnelles: . - Rappelez-vous que si les variables sont directement proportionnelles, elles suivront le modèle .
- Utilisez l'algèbre pour réécrire l'équation.
- Isoler le variable en divisant chaque côté par :
- Isoler le variable en divisant chaque côté par :
- Déterminer si l'équation réécrite suit le modèle . Dans ce cas, l’équation ne le fait pas, donc les variables ne sont pas directement proportionnelles. En fait, ils sont inversement proportionnels.[7]
-
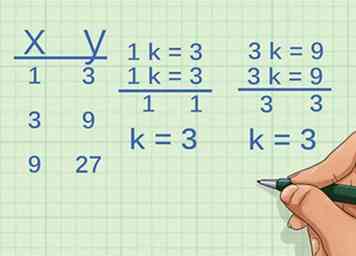 2 Considérons le jeu de points suivant. Les variables sont-elles directement proportionnelles?
2 Considérons le jeu de points suivant. Les variables sont-elles directement proportionnelles?
- Déterminer la croissance de . Pour cela, trouvez le facteur que vous multipliez par la première coordonnée x pour atteindre la deuxième coordonnée:
La coordonnée x augmente donc d'un facteur de 3. - Déterminer la croissance de :
Ainsi, la coordonnée y augmente de 3. - Comparez le facteur, ou la constante, des deux variables. Ils augmentent tous les deux d'un facteur 3. Par conséquent, les variables sont directement proportionnelles.
- Déterminer la croissance de . Pour cela, trouvez le facteur que vous multipliez par la première coordonnée x pour atteindre la deuxième coordonnée:
-
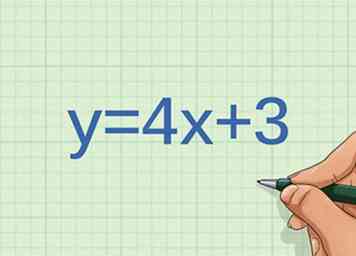 3 Considérons un graphique de la ligne . Le graphique montre-t-il une proportion directe entre les variables?
3 Considérons un graphique de la ligne . Le graphique montre-t-il une proportion directe entre les variables? - Notez si la ligne est droite. Comme l'équation de la ligne est en forme de pente, elle a une pente constante, ce qui signifie que la ligne est droite. Donc, potentiellement, les variables sont directement proportionnelles.
- Détermine l'ordonnée à l'origine. Si les variables sont directement proportionnelles, la ligne passera par le point . L'ordonnée à l'origine de cette ligne est le point . Les variables ne sont donc pas directement proportionnelles.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
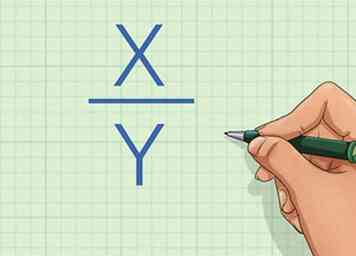 1 Comprendre la proportion directe. Deux variables sont en proportion directe si chaque variable change au même rythme.[1] En d'autres termes, si
1 Comprendre la proportion directe. Deux variables sont en proportion directe si chaque variable change au même rythme.[1] En d'autres termes, si 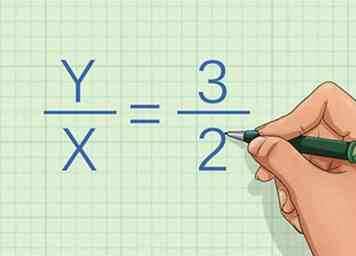 2 Notez l'équation de la ligne. L'équation aura deux variables et une constante. Si vous ne recevez pas l'équation, vous ne pouvez pas utiliser cette méthode.
2 Notez l'équation de la ligne. L'équation aura deux variables et une constante. Si vous ne recevez pas l'équation, vous ne pouvez pas utiliser cette méthode. 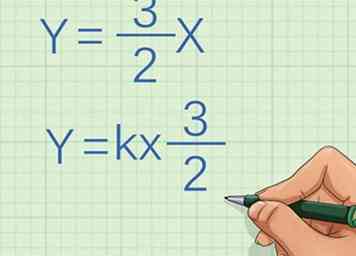 3 Réécrivez l'équation sous forme de proportion directe ou de variation. L'équation est
3 Réécrivez l'équation sous forme de proportion directe ou de variation. L'équation est  1 Identifiez les coordonnées x des deux premiers points. Vous devriez recevoir une liste de coordonnées ou avoir un graphique à partir duquel vous pouvez déterminer les coordonnées des points. Si vous n'avez pas les coordonnées des points sur la ligne, vous ne pouvez pas utiliser cette méthode.
1 Identifiez les coordonnées x des deux premiers points. Vous devriez recevoir une liste de coordonnées ou avoir un graphique à partir duquel vous pouvez déterminer les coordonnées des points. Si vous n'avez pas les coordonnées des points sur la ligne, vous ne pouvez pas utiliser cette méthode. 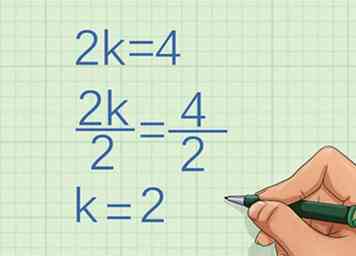 2 Déterminer le facteur par lequel le
2 Déterminer le facteur par lequel le 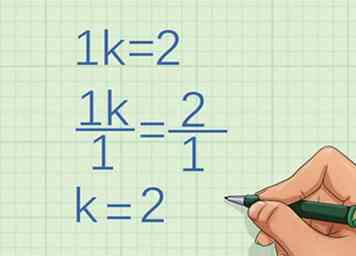 3 Déterminer le facteur par lequel le
3 Déterminer le facteur par lequel le  4 Comparez les constantes des deux variables. Si
4 Comparez les constantes des deux variables. Si  1 Notez si la ligne est droite. Lorsque deux variables sont en proportion, la ligne les représentant sera droite.[4] Cela signifie que la pente de la ligne est constante ou suit l’équation
1 Notez si la ligne est droite. Lorsque deux variables sont en proportion, la ligne les représentant sera droite.[4] Cela signifie que la pente de la ligne est constante ou suit l’équation  2 Détermine l'ordonnée à l'origine. L'ordonnée à l'origine est le point où la ligne traverse l'axe des y. Lorsque deux variables sont directement proportionnelles, lorsqu'elles sont représentées graphiquement, leur ligne traverse l'origine. L'origine est au point
2 Détermine l'ordonnée à l'origine. L'ordonnée à l'origine est le point où la ligne traverse l'axe des y. Lorsque deux variables sont directement proportionnelles, lorsqu'elles sont représentées graphiquement, leur ligne traverse l'origine. L'origine est au point  3 Trouvez les coordonnées de deux points sur la ligne. Comparez les coordonnées entre elles et déterminez si chaque coordonnée a changé du même facteur.[6] C'est-à-dire, déterminer si la constante (
3 Trouvez les coordonnées de deux points sur la ligne. Comparez les coordonnées entre elles et déterminez si chaque coordonnée a changé du même facteur.[6] C'est-à-dire, déterminer si la constante (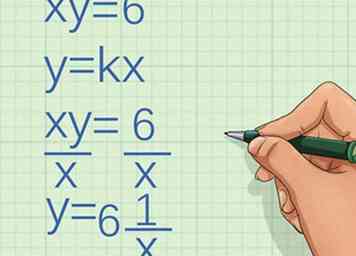 1 Regardez l'équation. Déterminer si les deux variables sont directement proportionnelles:
1 Regardez l'équation. Déterminer si les deux variables sont directement proportionnelles: 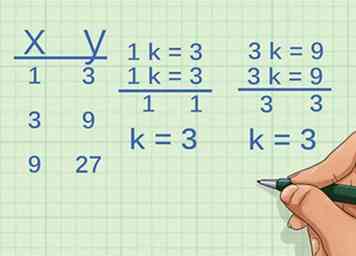 2 Considérons le jeu de points suivant. Les variables sont-elles directement proportionnelles?
2 Considérons le jeu de points suivant. Les variables sont-elles directement proportionnelles?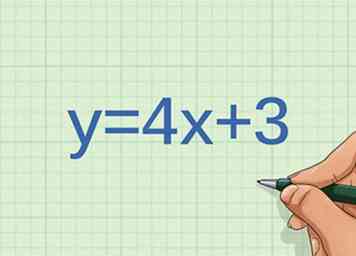 3 Considérons un graphique de la ligne
3 Considérons un graphique de la ligne