Le domaine d'une fonction est l'ensemble des nombres pouvant entrer dans une fonction donnée. En d'autres termes, c'est l'ensemble des valeurs x que vous pouvez ajouter à une équation donnée. L'ensemble des valeurs y possibles est appelé la plage. Si vous voulez savoir comment trouver le domaine d'une fonction dans diverses situations, suivez ces étapes.
Méthode One of Six:
Apprendre les bases
-
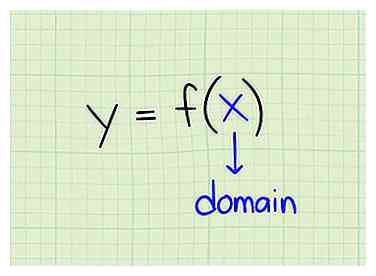 1 Apprenez la définition du domaine. Le domaine est défini comme l'ensemble des valeurs d'entrée pour lesquelles la fonction produit une valeur de sortie. En d'autres termes, le domaine est l'ensemble complet des valeurs x pouvant être intégrées à une fonction pour produire une valeur y.
1 Apprenez la définition du domaine. Le domaine est défini comme l'ensemble des valeurs d'entrée pour lesquelles la fonction produit une valeur de sortie. En d'autres termes, le domaine est l'ensemble complet des valeurs x pouvant être intégrées à une fonction pour produire une valeur y. -
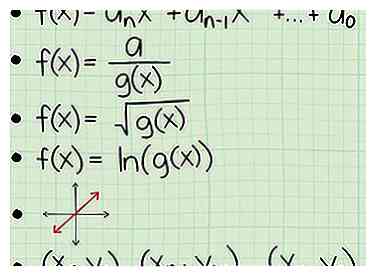 2 Apprenez à trouver le domaine d'une variété de fonctions. Le type de fonction déterminera la meilleure méthode pour trouver un domaine. Voici les bases que vous devez connaître pour chaque type de fonction, qui sera expliqué dans la section suivante:
2 Apprenez à trouver le domaine d'une variété de fonctions. Le type de fonction déterminera la meilleure méthode pour trouver un domaine. Voici les bases que vous devez connaître pour chaque type de fonction, qui sera expliqué dans la section suivante: - Une fonction polynomiale sans radicaux ni variables dans le dénominateur. Pour ce type de fonction, le domaine est constitué de tous les nombres réels.
- Une fonction avec une fraction avec une variable dans le dénominateur. Pour trouver le domaine de ce type de fonction, définissez le fond égal à zéro et excluez la valeur x que vous trouvez lorsque vous résolvez l'équation.
- Une fonction avec une variable à l'intérieur d'un signe radical. Pour trouver le domaine de ce type de fonction, définissez simplement les termes à l'intérieur du signe radical sur> 0 et résolvez pour trouver les valeurs qui fonctionneraient pour x.
- Une fonction utilisant le log naturel (ln). Il suffit de définir les termes entre parenthèses sur> 0 et de résoudre.
- Un graphique. Consultez le graphique pour voir quelles valeurs fonctionnent pour x.
- Une relation. Ce sera une liste de coordonnées x et y. Votre domaine sera simplement une liste de coordonnées x.
-
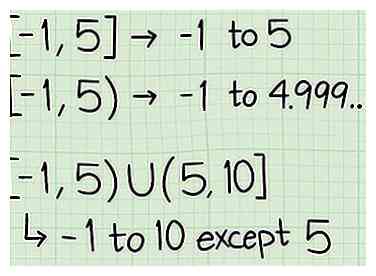 3 Indiquez correctement le domaine. La notation correcte pour le domaine est facile à apprendre, mais il est important que vous l'écriviez correctement pour exprimer la bonne réponse et obtenir des points complets sur les devoirs et les tests. Voici quelques points à connaître sur l'écriture du domaine d'une fonction:
3 Indiquez correctement le domaine. La notation correcte pour le domaine est facile à apprendre, mais il est important que vous l'écriviez correctement pour exprimer la bonne réponse et obtenir des points complets sur les devoirs et les tests. Voici quelques points à connaître sur l'écriture du domaine d'une fonction: - Le format d’expression du domaine est une parenthèse / parenthèse ouverte, suivie des deux extrémités du domaine séparées par une virgule, suivies d’une parenthèse / parenthèse fermée.
- Par exemple, [-1,5]. Cela signifie que le domaine passe de -1 à 5.
- Utilisez des crochets tels que [ et ] pour indiquer qu'un numéro est inclus dans le domaine.
- Donc, dans l'exemple, [-1,5), le domaine comprend -1.
- Utilisez des parenthèses telles que ( et ) pour indiquer qu'un numéro n'est pas inclus dans le domaine.
- Donc, dans l'exemple, [-1,5), 5 n'est pas inclus dans le domaine. Le domaine s'arrête arbitrairement à 5, c'est-à-dire 4,999…
- Utilisez "U" (signifiant "union") pour connecter des parties du domaine séparées par un espace. "
- Par exemple, [-1,5) U (5,10). Cela signifie que le domaine va de -1 à 10, inclus, mais qu'il y a un espace dans le domaine à 5. Cela peut être le résultat de, pour Par exemple, une fonction avec «x - 5» dans le dénominateur.
- Vous pouvez utiliser autant de symboles "U" que nécessaire si le domaine comporte plusieurs lacunes.
- Utilisez des signes d'infini et d'infini négatif pour exprimer que le domaine se poursuit infiniment dans les deux sens.
- Toujours utiliser (), pas [], avec des symboles infinis.
- Le format d’expression du domaine est une parenthèse / parenthèse ouverte, suivie des deux extrémités du domaine séparées par une virgule, suivies d’une parenthèse / parenthèse fermée.
Méthode deux sur six:
Trouver le domaine d'une fonction avec une fraction
-
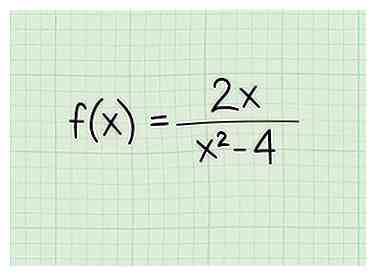 1 Écrivez le problème. Disons que vous travaillez avec le problème suivant:
1 Écrivez le problème. Disons que vous travaillez avec le problème suivant: - f (x) = 2x / (x2 - 4)
-
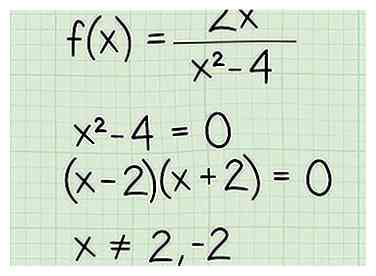 2 Définissez le dénominateur égal à zéro pour les fractions avec une variable dans le dénominateur. Lorsque vous trouvez le domaine d'une fonction fractionnaire, vous devez exclure toutes les valeurs x qui rendent le dénominateur égal à zéro, car vous ne pouvez jamais diviser par zéro. Donc, écrivez le dénominateur comme une équation et définissez-le égal à 0. Voici comment procéder:
2 Définissez le dénominateur égal à zéro pour les fractions avec une variable dans le dénominateur. Lorsque vous trouvez le domaine d'une fonction fractionnaire, vous devez exclure toutes les valeurs x qui rendent le dénominateur égal à zéro, car vous ne pouvez jamais diviser par zéro. Donc, écrivez le dénominateur comme une équation et définissez-le égal à 0. Voici comment procéder: - f (x) = 2x / (x2 - 4)
- X2 - 4 = 0
- (x - 2) (x + 2) = 0
- x ≠ (2, - 2)
-
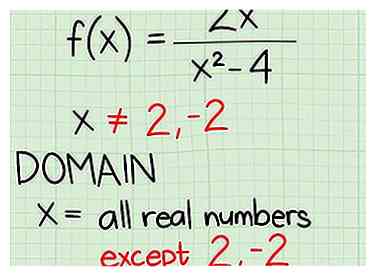 3 Indiquez le domaine. Voici comment vous le faites:
3 Indiquez le domaine. Voici comment vous le faites: - x = tous les nombres réels sauf 2 et -2
Méthode trois sur six:
Trouver le domaine d'une fonction avec une racine carrée
-
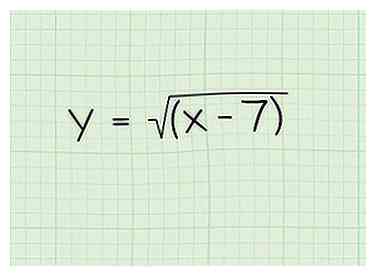 1 Écrivez le problème. Disons que vous travaillez avec le problème suivant: Y = √ (x-7)
1 Écrivez le problème. Disons que vous travaillez avec le problème suivant: Y = √ (x-7) -
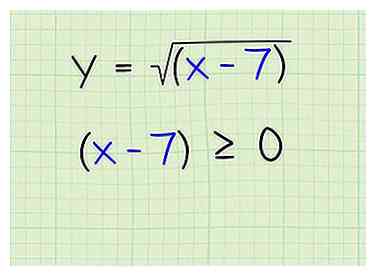 2 Définissez les termes à l'intérieur du radicand pour qu'ils soient supérieurs ou égaux à 0. Vous ne pouvez pas prendre la racine carrée d'un nombre négatif, même si vous pouvez prendre la racine carrée de 0. Définissez donc les termes à l'intérieur du radicand pour qu'ils soient supérieurs ou égaux à 0. Notez que cela ne s'applique pas uniquement aux racines carrées, mais à toutes les racines paires. Cela ne s'applique cependant pas aux racines impaires, car il est parfaitement correct d'avoir des négatifs sous des racines impaires. Voici comment:
2 Définissez les termes à l'intérieur du radicand pour qu'ils soient supérieurs ou égaux à 0. Vous ne pouvez pas prendre la racine carrée d'un nombre négatif, même si vous pouvez prendre la racine carrée de 0. Définissez donc les termes à l'intérieur du radicand pour qu'ils soient supérieurs ou égaux à 0. Notez que cela ne s'applique pas uniquement aux racines carrées, mais à toutes les racines paires. Cela ne s'applique cependant pas aux racines impaires, car il est parfaitement correct d'avoir des négatifs sous des racines impaires. Voici comment: - x-7 ≧ 0
-
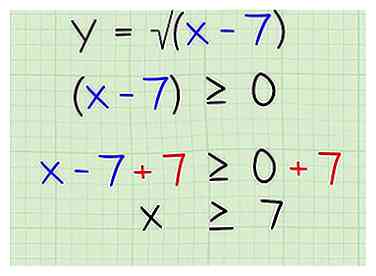 3 Isoler la variable. Maintenant, pour isoler x sur le côté gauche de l'équation, ajoutez simplement 7 aux deux côtés, de sorte que vous vous retrouviez avec les éléments suivants:
3 Isoler la variable. Maintenant, pour isoler x sur le côté gauche de l'équation, ajoutez simplement 7 aux deux côtés, de sorte que vous vous retrouviez avec les éléments suivants: - x ≧ 7
-
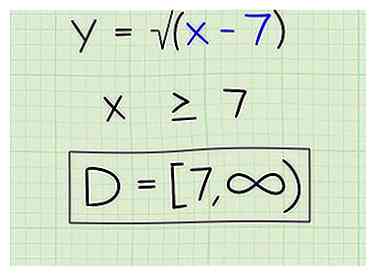 4 Indiquez le domaine correctement. Voici comment vous l'écririez:
4 Indiquez le domaine correctement. Voici comment vous l'écririez: - D = [7, ∞]
-
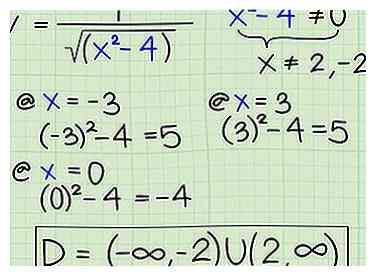 5 Trouvez le domaine d'une fonction avec une racine carrée lorsqu'il existe plusieurs solutions. Disons que vous travaillez avec la fonction suivante: Y = 1 / √ (̅x2 -4). Lorsque vous factorisez le dénominateur et que vous le définissez égal à zéro, vous obtenez x ≠ (2, - 2). Voici où vous allez à partir de là:
5 Trouvez le domaine d'une fonction avec une racine carrée lorsqu'il existe plusieurs solutions. Disons que vous travaillez avec la fonction suivante: Y = 1 / √ (̅x2 -4). Lorsque vous factorisez le dénominateur et que vous le définissez égal à zéro, vous obtenez x ≠ (2, - 2). Voici où vous allez à partir de là: - Maintenant, vérifiez la zone en dessous de -2 (en branchant -3, par exemple), pour voir si les nombres en dessous de -2 peuvent être insérés dans le dénominateur pour donner un nombre supérieur à 0. Ils le font.
- (-3)2 - 4 = 5
- Maintenant, vérifiez la zone entre -2 et 2. Choisissez 0, par exemple.
- 02 - 4 = -4, donc vous savez que les nombres entre -2 et 2 ne fonctionnent pas.
- Maintenant, essayez un nombre supérieur à 2, tel que +3.
- 32 - 4 = 5, donc les nombres supérieurs à 2 fonctionnent.
- Écrivez le domaine lorsque vous avez terminé. Voici comment vous écrivez le domaine:
- D = (-∞, -2) U (2, ∞)
- Maintenant, vérifiez la zone en dessous de -2 (en branchant -3, par exemple), pour voir si les nombres en dessous de -2 peuvent être insérés dans le dénominateur pour donner un nombre supérieur à 0. Ils le font.
Méthode quatre sur six:
Recherche du domaine d'une fonction à l'aide d'un journal naturel
-
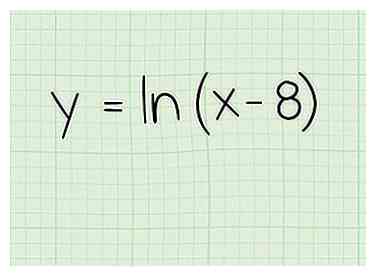 1 Écrivez le problème. Disons que vous travaillez avec celui-ci:
1 Écrivez le problème. Disons que vous travaillez avec celui-ci: - f (x) = ln (x-8)
-
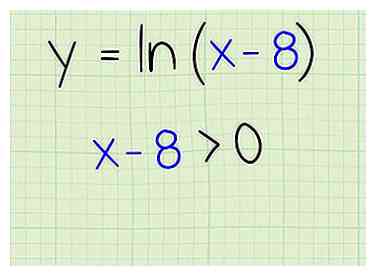 2 Définissez les termes entre parenthèses à plus de zéro. Le journal naturel doit être un nombre positif, définissez donc les termes entre parenthèses sur une valeur supérieure à zéro pour que cela soit possible. Voici ce que vous faites:
2 Définissez les termes entre parenthèses à plus de zéro. Le journal naturel doit être un nombre positif, définissez donc les termes entre parenthèses sur une valeur supérieure à zéro pour que cela soit possible. Voici ce que vous faites: - x - 8> 0
-
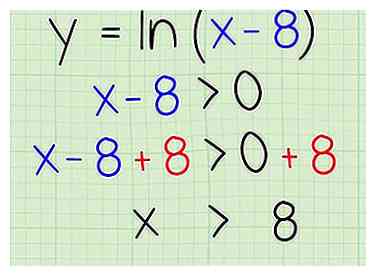 3 Résoudre. Isolez simplement la variable x en ajoutant 8 aux deux côtés. Voici comment:
3 Résoudre. Isolez simplement la variable x en ajoutant 8 aux deux côtés. Voici comment: - x - 8 + 8> 0 + 8
- x> 8
-
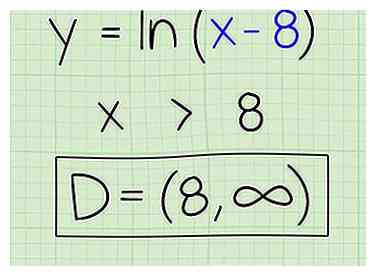 4 Indiquez le domaine. Montrer que le domaine pour cette équation est égal à tous les nombres supérieurs à 8 jusqu'à l'infini. Voici comment:
4 Indiquez le domaine. Montrer que le domaine pour cette équation est égal à tous les nombres supérieurs à 8 jusqu'à l'infini. Voici comment: - D = (8, ∞)
Méthode cinq sur six:
Recherche du domaine d'une fonction à l'aide d'un graphique
-
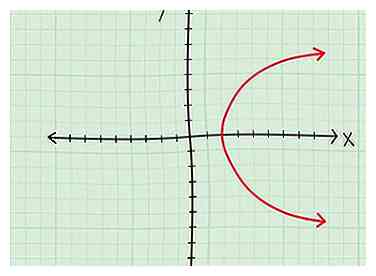 1 Regardez le graphique.
1 Regardez le graphique. -
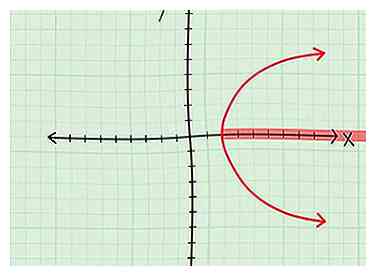 2 Découvrez les valeurs x incluses dans le graphique. Cela peut être plus facile à dire qu'à faire, mais voici quelques conseils:
2 Découvrez les valeurs x incluses dans le graphique. Cela peut être plus facile à dire qu'à faire, mais voici quelques conseils: - Une ligne. Si vous voyez une ligne sur le graphique qui s'étend à l'infini, alors tout les versions de x seront éventuellement couvertes, donc le domaine est égal à tous les nombres réels.
- Une parabole normale. Si vous voyez une parabole qui est tournée vers le haut ou vers le bas, alors oui, le domaine sera composé de tous les nombres réels, car tous les nombres sur l'axe des x seront éventuellement couverts.
- Une parabole latérale. Maintenant, si vous avez une parabole avec un sommet à (4,0) qui s'étend infiniment vers la droite, votre domaine est D = [4, ∞]
-
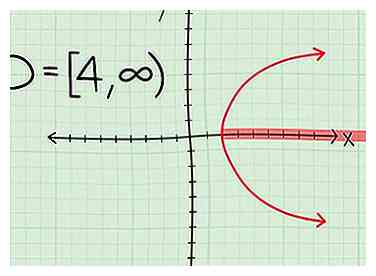 3 Indiquez le domaine. Indiquez simplement le domaine en fonction du type de graphique avec lequel vous travaillez. Si vous êtes incertain et que vous connaissez l'équation de la ligne, branchez les coordonnées x dans la fonction à vérifier.
3 Indiquez le domaine. Indiquez simplement le domaine en fonction du type de graphique avec lequel vous travaillez. Si vous êtes incertain et que vous connaissez l'équation de la ligne, branchez les coordonnées x dans la fonction à vérifier.
Méthode six sur six:
Recherche du domaine d'une fonction à l'aide d'une relation
-
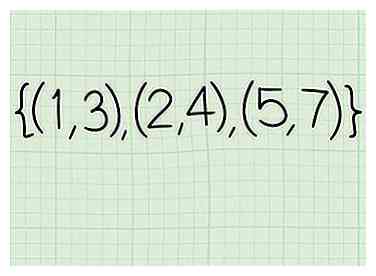 1 Notez la relation. Une relation est juste un ensemble de coordonnées x et y. Disons que vous travaillez avec les coordonnées suivantes: (1, 3), (2, 4), (5, 7)
1 Notez la relation. Une relation est juste un ensemble de coordonnées x et y. Disons que vous travaillez avec les coordonnées suivantes: (1, 3), (2, 4), (5, 7) -
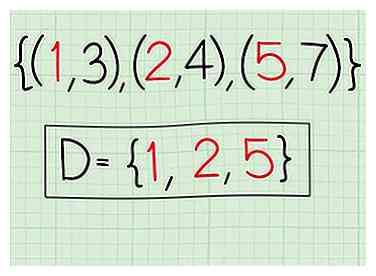 2 Notez les coordonnées x. Ils sont: 1, 2, 5.
2 Notez les coordonnées x. Ils sont: 1, 2, 5. -
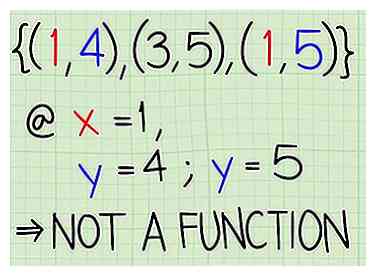 3 Indiquez le domaine. D = 1, 2, 5
3 Indiquez le domaine. D = 1, 2, 5 - 4 Assurez-vous que la relation est une fonction. Pour qu'une relation soit une fonction, chaque fois que vous mettez une coordonnée x numérique, vous devriez obtenir la même coordonnée y. Donc, si vous mettez 3 pour x, vous devriez toujours obtenir 6 pour y, et ainsi de suite. La relation suivante est ne pas une fonction parce que vous obtenez deux valeurs différentes de "y" pour chaque valeur de "x": (1, 4), (3, 5), (1, 5).[1]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Apprenez la définition du domaine. Le domaine est défini comme l'ensemble des valeurs d'entrée pour lesquelles la fonction produit une valeur de sortie. En d'autres termes, le domaine est l'ensemble complet des valeurs x pouvant être intégrées à une fonction pour produire une valeur y.
1 Apprenez la définition du domaine. Le domaine est défini comme l'ensemble des valeurs d'entrée pour lesquelles la fonction produit une valeur de sortie. En d'autres termes, le domaine est l'ensemble complet des valeurs x pouvant être intégrées à une fonction pour produire une valeur y. 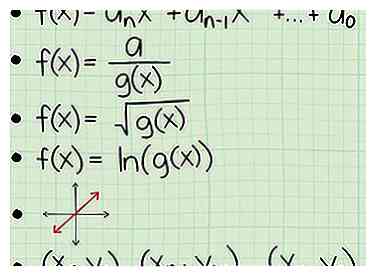 2 Apprenez à trouver le domaine d'une variété de fonctions. Le type de fonction déterminera la meilleure méthode pour trouver un domaine. Voici les bases que vous devez connaître pour chaque type de fonction, qui sera expliqué dans la section suivante:
2 Apprenez à trouver le domaine d'une variété de fonctions. Le type de fonction déterminera la meilleure méthode pour trouver un domaine. Voici les bases que vous devez connaître pour chaque type de fonction, qui sera expliqué dans la section suivante: 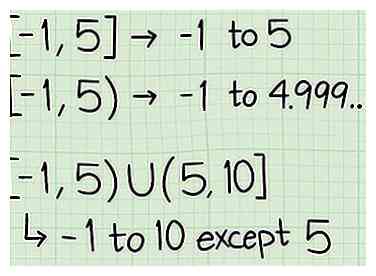 3 Indiquez correctement le domaine. La notation correcte pour le domaine est facile à apprendre, mais il est important que vous l'écriviez correctement pour exprimer la bonne réponse et obtenir des points complets sur les devoirs et les tests. Voici quelques points à connaître sur l'écriture du domaine d'une fonction:
3 Indiquez correctement le domaine. La notation correcte pour le domaine est facile à apprendre, mais il est important que vous l'écriviez correctement pour exprimer la bonne réponse et obtenir des points complets sur les devoirs et les tests. Voici quelques points à connaître sur l'écriture du domaine d'une fonction: 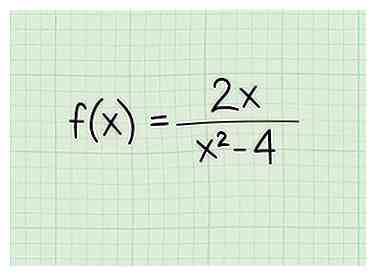 1 Écrivez le problème. Disons que vous travaillez avec le problème suivant:
1 Écrivez le problème. Disons que vous travaillez avec le problème suivant: 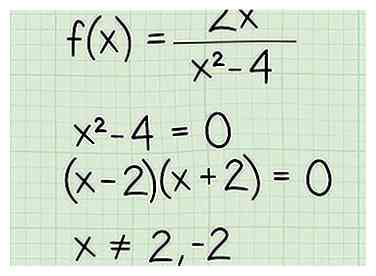 2 Définissez le dénominateur égal à zéro pour les fractions avec une variable dans le dénominateur. Lorsque vous trouvez le domaine d'une fonction fractionnaire, vous devez exclure toutes les valeurs x qui rendent le dénominateur égal à zéro, car vous ne pouvez jamais diviser par zéro. Donc, écrivez le dénominateur comme une équation et définissez-le égal à 0. Voici comment procéder:
2 Définissez le dénominateur égal à zéro pour les fractions avec une variable dans le dénominateur. Lorsque vous trouvez le domaine d'une fonction fractionnaire, vous devez exclure toutes les valeurs x qui rendent le dénominateur égal à zéro, car vous ne pouvez jamais diviser par zéro. Donc, écrivez le dénominateur comme une équation et définissez-le égal à 0. Voici comment procéder: 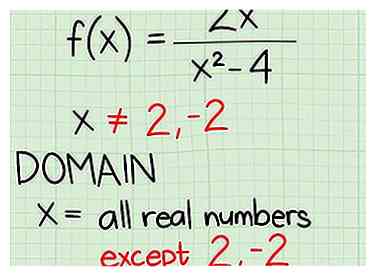 3 Indiquez le domaine. Voici comment vous le faites:
3 Indiquez le domaine. Voici comment vous le faites: 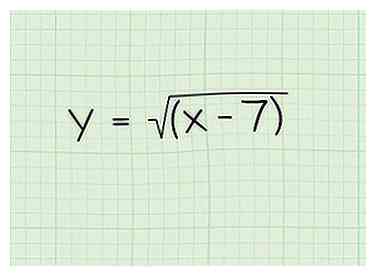 1 Écrivez le problème. Disons que vous travaillez avec le problème suivant: Y = √ (x-7)
1 Écrivez le problème. Disons que vous travaillez avec le problème suivant: Y = √ (x-7) 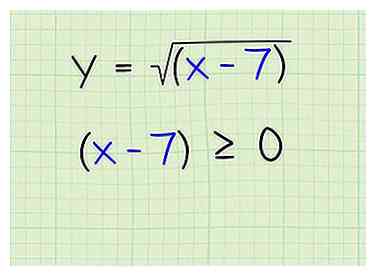 2 Définissez les termes à l'intérieur du radicand pour qu'ils soient supérieurs ou égaux à 0. Vous ne pouvez pas prendre la racine carrée d'un nombre négatif, même si vous pouvez prendre la racine carrée de 0. Définissez donc les termes à l'intérieur du radicand pour qu'ils soient supérieurs ou égaux à 0. Notez que cela ne s'applique pas uniquement aux racines carrées, mais à toutes les racines paires. Cela ne s'applique cependant pas aux racines impaires, car il est parfaitement correct d'avoir des négatifs sous des racines impaires. Voici comment:
2 Définissez les termes à l'intérieur du radicand pour qu'ils soient supérieurs ou égaux à 0. Vous ne pouvez pas prendre la racine carrée d'un nombre négatif, même si vous pouvez prendre la racine carrée de 0. Définissez donc les termes à l'intérieur du radicand pour qu'ils soient supérieurs ou égaux à 0. Notez que cela ne s'applique pas uniquement aux racines carrées, mais à toutes les racines paires. Cela ne s'applique cependant pas aux racines impaires, car il est parfaitement correct d'avoir des négatifs sous des racines impaires. Voici comment: 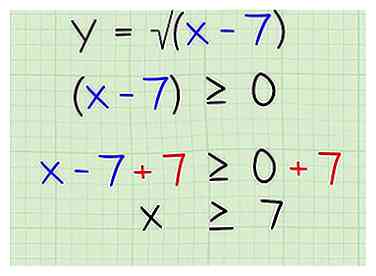 3 Isoler la variable. Maintenant, pour isoler x sur le côté gauche de l'équation, ajoutez simplement 7 aux deux côtés, de sorte que vous vous retrouviez avec les éléments suivants:
3 Isoler la variable. Maintenant, pour isoler x sur le côté gauche de l'équation, ajoutez simplement 7 aux deux côtés, de sorte que vous vous retrouviez avec les éléments suivants: 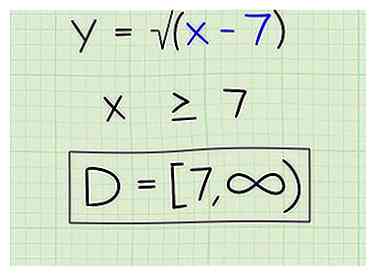 4 Indiquez le domaine correctement. Voici comment vous l'écririez:
4 Indiquez le domaine correctement. Voici comment vous l'écririez: 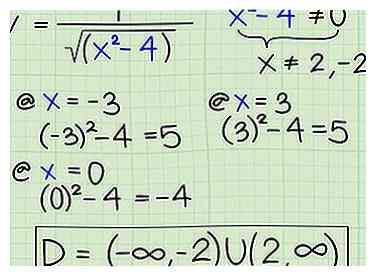 5 Trouvez le domaine d'une fonction avec une racine carrée lorsqu'il existe plusieurs solutions. Disons que vous travaillez avec la fonction suivante: Y = 1 / √ (̅x2 -4). Lorsque vous factorisez le dénominateur et que vous le définissez égal à zéro, vous obtenez x ≠ (2, - 2). Voici où vous allez à partir de là:
5 Trouvez le domaine d'une fonction avec une racine carrée lorsqu'il existe plusieurs solutions. Disons que vous travaillez avec la fonction suivante: Y = 1 / √ (̅x2 -4). Lorsque vous factorisez le dénominateur et que vous le définissez égal à zéro, vous obtenez x ≠ (2, - 2). Voici où vous allez à partir de là: 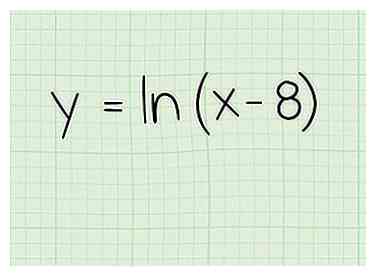 1 Écrivez le problème. Disons que vous travaillez avec celui-ci:
1 Écrivez le problème. Disons que vous travaillez avec celui-ci: 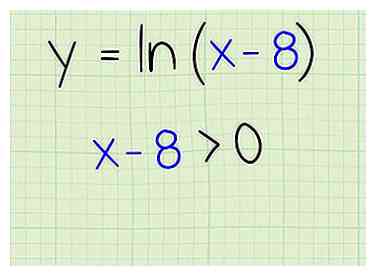 2 Définissez les termes entre parenthèses à plus de zéro. Le journal naturel doit être un nombre positif, définissez donc les termes entre parenthèses sur une valeur supérieure à zéro pour que cela soit possible. Voici ce que vous faites:
2 Définissez les termes entre parenthèses à plus de zéro. Le journal naturel doit être un nombre positif, définissez donc les termes entre parenthèses sur une valeur supérieure à zéro pour que cela soit possible. Voici ce que vous faites: 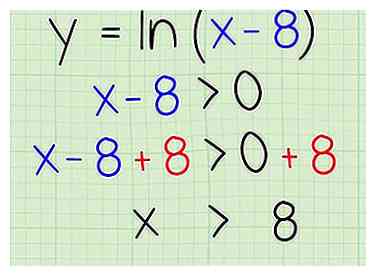 3 Résoudre. Isolez simplement la variable x en ajoutant 8 aux deux côtés. Voici comment:
3 Résoudre. Isolez simplement la variable x en ajoutant 8 aux deux côtés. Voici comment: 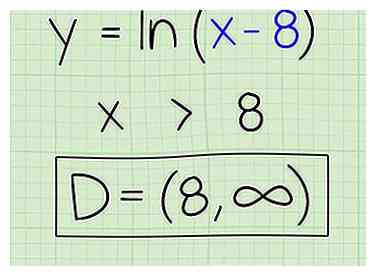 4 Indiquez le domaine. Montrer que le domaine pour cette équation est égal à tous les nombres supérieurs à 8 jusqu'à l'infini. Voici comment:
4 Indiquez le domaine. Montrer que le domaine pour cette équation est égal à tous les nombres supérieurs à 8 jusqu'à l'infini. Voici comment:  1 Regardez le graphique.
1 Regardez le graphique.  2 Découvrez les valeurs x incluses dans le graphique. Cela peut être plus facile à dire qu'à faire, mais voici quelques conseils:
2 Découvrez les valeurs x incluses dans le graphique. Cela peut être plus facile à dire qu'à faire, mais voici quelques conseils:  3 Indiquez le domaine. Indiquez simplement le domaine en fonction du type de graphique avec lequel vous travaillez. Si vous êtes incertain et que vous connaissez l'équation de la ligne, branchez les coordonnées x dans la fonction à vérifier.
3 Indiquez le domaine. Indiquez simplement le domaine en fonction du type de graphique avec lequel vous travaillez. Si vous êtes incertain et que vous connaissez l'équation de la ligne, branchez les coordonnées x dans la fonction à vérifier. 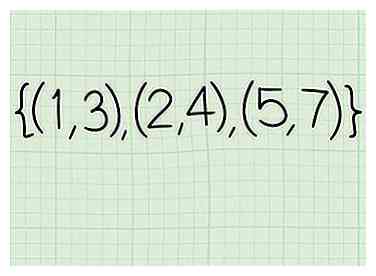 1 Notez la relation. Une relation est juste un ensemble de coordonnées x et y. Disons que vous travaillez avec les coordonnées suivantes: (1, 3), (2, 4), (5, 7)
1 Notez la relation. Une relation est juste un ensemble de coordonnées x et y. Disons que vous travaillez avec les coordonnées suivantes: (1, 3), (2, 4), (5, 7) 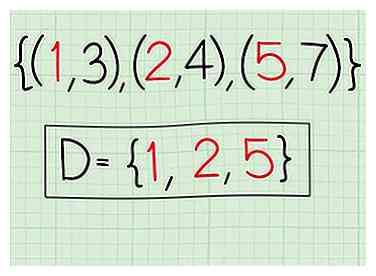 2 Notez les coordonnées x. Ils sont: 1, 2, 5.
2 Notez les coordonnées x. Ils sont: 1, 2, 5. 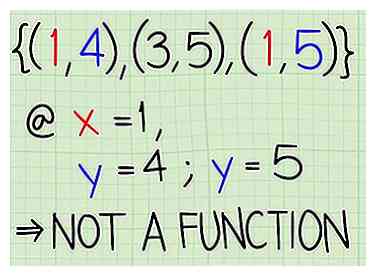 3 Indiquez le domaine. D = 1, 2, 5
3 Indiquez le domaine. D = 1, 2, 5