Contrairement à une ligne droite, la pente d'une courbe change constamment lorsque vous vous déplacez le long du graphique. Le calcul introduit les élèves à l’idée que chaque point de ce graphique pourrait être décrit avec une pente ou un «taux de changement instantané». La ligne tangente est une ligne droite avec cette pente, passant par ce point exact sur le graphique. Pour trouver l'équation de la tangente, vous devez savoir comment prendre la dérivée de l'équation originale.
Méthode One of Two:
Trouver l'équation d'une ligne tangente
-
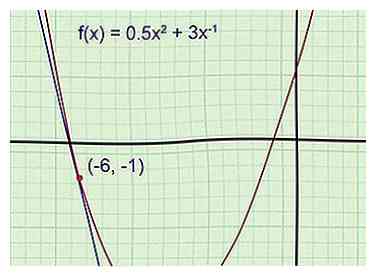 1 Esquissez la fonction et la ligne tangente (recommandé). Un graphique facilite le suivi du problème et vérifie la pertinence de la réponse. Dessinez la fonction sur un morceau de papier millimétré, en utilisant une calculatrice graphique comme référence si nécessaire. Esquissez la ligne tangente passant par le point donné. (Rappelez-vous que la ligne tangente traverse ce point et a la même pente que le graphique à cet endroit.)
1 Esquissez la fonction et la ligne tangente (recommandé). Un graphique facilite le suivi du problème et vérifie la pertinence de la réponse. Dessinez la fonction sur un morceau de papier millimétré, en utilisant une calculatrice graphique comme référence si nécessaire. Esquissez la ligne tangente passant par le point donné. (Rappelez-vous que la ligne tangente traverse ce point et a la même pente que le graphique à cet endroit.) - Exemple 1: Esquisser le graphique de la parabole . Dessine la tangente passant par le point (-6, -1).
Vous ne connaissez pas encore l'équation de la tangente, mais vous pouvez déjà dire que sa pente est négative et que son ordonnée à l'origine est négative (bien au-dessous du sommet de la parabole avec la valeur y -5,5). Si votre réponse finale ne correspond pas à ces détails, vous saurez vérifier votre travail à la recherche d’erreurs.
- Exemple 1: Esquisser le graphique de la parabole . Dessine la tangente passant par le point (-6, -1).
-
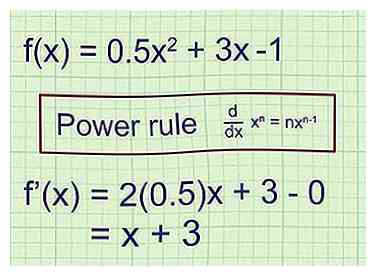 2 Prenez le premier dérivé pour trouver l'équation du pente de la ligne tangente. Pour la fonction f (x), la première dérivée f '(x) représente l’équation de la pente de la tangente en tout point de f (x). Il y a plusieurs façons de prendre des dérivés. Voici un exemple simple utilisant la règle de puissance:[1]
2 Prenez le premier dérivé pour trouver l'équation du pente de la ligne tangente. Pour la fonction f (x), la première dérivée f '(x) représente l’équation de la pente de la tangente en tout point de f (x). Il y a plusieurs façons de prendre des dérivés. Voici un exemple simple utilisant la règle de puissance:[1] - Exemple 1 (suite): Le graphique est décrit par la fonction .
Rappelez-vous la règle de puissance lors de la prise de dérivés: .
La première dérivée de la fonction = f '(x) = (2) (0.5) x + 3 - 0.
f '(x) = x + 3. Branchez une valeur a pour x dans cette équation, et le résultat sera la pente de la ligne tangente à f (x) au point x = a.
- Exemple 1 (suite): Le graphique est décrit par la fonction .
-
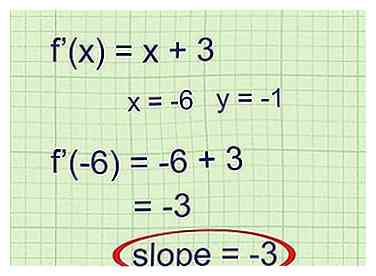 3 Entrez la valeur x du point que vous étudiez. Lisez le problème pour découvrir les coordonnées du point pour lequel vous trouvez la ligne tangente. Entrez la coordonnée x de ce point dans f '(x). La sortie est la pente de la ligne tangente à ce point.
3 Entrez la valeur x du point que vous étudiez. Lisez le problème pour découvrir les coordonnées du point pour lequel vous trouvez la ligne tangente. Entrez la coordonnée x de ce point dans f '(x). La sortie est la pente de la ligne tangente à ce point. - Exemple 1 (suite): Le point mentionné dans le problème est (-6, -1). Utilisez la coordonnée x -6 comme entrée pour f '(x):
f '(- 6) = -6 + 3 = -3
La pente de la ligne tangente est de -3.
- Exemple 1 (suite): Le point mentionné dans le problème est (-6, -1). Utilisez la coordonnée x -6 comme entrée pour f '(x):
-
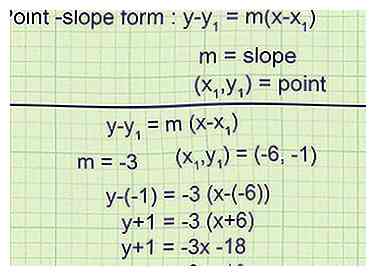 4 Écrivez l'équation de la ligne tangente en forme de pente ponctuelle. La forme point-pente d'une équation linéaire est , où m est la pente et est un point sur la ligne.[2] Vous avez maintenant toutes les informations nécessaires pour écrire l'équation de la ligne tangente sous cette forme.
4 Écrivez l'équation de la ligne tangente en forme de pente ponctuelle. La forme point-pente d'une équation linéaire est , où m est la pente et est un point sur la ligne.[2] Vous avez maintenant toutes les informations nécessaires pour écrire l'équation de la ligne tangente sous cette forme. - Exemple 1 (suite):
La pente de la ligne est de -3, donc
La ligne tangente passe par (-6, -1), l’équation finale est donc
Simplifier à
- Exemple 1 (suite):
-
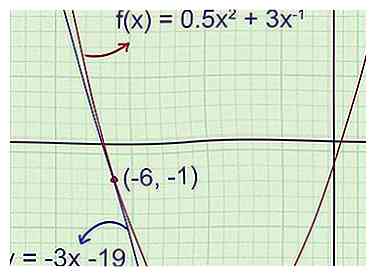 5 Confirmez l'équation sur votre graphique. Si vous avez une calculatrice graphique, tracez la fonction d'origine et la ligne tangente pour vérifier que vous avez la bonne réponse. Si vous travaillez sur papier, reportez-vous à votre graphique précédent pour vous assurer qu’il n’ya pas d’erreurs flagrantes dans votre réponse.
5 Confirmez l'équation sur votre graphique. Si vous avez une calculatrice graphique, tracez la fonction d'origine et la ligne tangente pour vérifier que vous avez la bonne réponse. Si vous travaillez sur papier, reportez-vous à votre graphique précédent pour vous assurer qu’il n’ya pas d’erreurs flagrantes dans votre réponse. - Exemple 1 (suite): L'esquisse initiale a montré que la pente de la tangente était négative et que l'ordonnée à l'origine était bien inférieure à -5,5. L'équation de la ligne tangente que nous avons trouvée est y = -3x - 19 dans la forme d'interception de pente, ce qui signifie que -3 est la pente et -19 est l'ordonnée à l'origine. Ces deux attributs correspondent aux prévisions initiales.
-
 6 Essayez un problème plus difficile. Voici un aperçu de tout le processus à nouveau. Cette fois, le but est de trouver la ligne tangente à à x = 2:
6 Essayez un problème plus difficile. Voici un aperçu de tout le processus à nouveau. Cette fois, le but est de trouver la ligne tangente à à x = 2: - En utilisant la règle de puissance, la première dérivée . Cette fonction nous indiquera la pente de la tangente.
- Puisque x = 2, trouvez . C'est la pente à x = 2.
- Notez que nous n'avons pas de point cette fois, seulement une coordonnée x. Pour trouver la coordonnée y, branchez x = 2 dans la fonction initiale: . Le point est (2,27).
- Écrivez l'équation de la ligne tangente sous forme de pente de point:
Si nécessaire, simplifiez pour y = 25x - 23.
Méthode deux sur deux:
Résolution de problèmes connexes
-
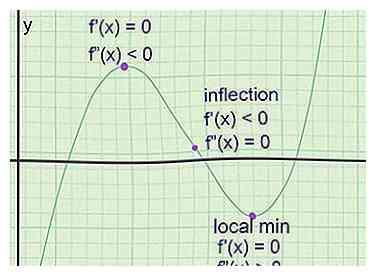 1 Trouvez les points extrêmes sur un graphique. Ce sont des points où le graphique atteint un maximum local (un point supérieur aux points de chaque côté) ou un minimum local (inférieur aux points de chaque côté). La ligne tangente a toujours une pente de 0 à ces points (une ligne horizontale), mais une pente nulle seule ne garantit pas un point extrême. Voici comment les trouver:[3]
1 Trouvez les points extrêmes sur un graphique. Ce sont des points où le graphique atteint un maximum local (un point supérieur aux points de chaque côté) ou un minimum local (inférieur aux points de chaque côté). La ligne tangente a toujours une pente de 0 à ces points (une ligne horizontale), mais une pente nulle seule ne garantit pas un point extrême. Voici comment les trouver:[3] - Prenez la première dérivée de la fonction pour obtenir f '(x), l'équation de la pente de la tangente.
- Résoudre pour f '(x) = 0 pour trouver possible points extrêmes.
- Prenez la seconde dérivée pour obtenir f "(x), l’équation qui vous indique à quelle vitesse la pente de la tangente change.
- Pour chaque point extrême possible, branchez la coordonnée x une dans f "(x). Si f" (a) est positif, il y a un minimum local à une. Si f "(a) est négatif, il y a un maximum local. Si f" (a) est 0, il y a un point d'inflexion, pas un point extrême.
- S'il y a un maximum ou un minimum à une, trouvez f (a) pour obtenir la coordonnée y.
-
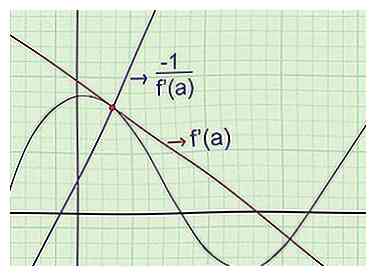 2 Trouvez l'équation de la normale. La "normale" à une courbe à un point particulier passe par ce point, mais a une pente perpendiculaire à une tangente. Pour trouver l'équation de la normale, profitez du fait que (pente de la tangente) (pente de la normale) = -1, quand elles passent toutes deux par le même point du graphique.[4] En d'autres termes:
2 Trouvez l'équation de la normale. La "normale" à une courbe à un point particulier passe par ce point, mais a une pente perpendiculaire à une tangente. Pour trouver l'équation de la normale, profitez du fait que (pente de la tangente) (pente de la normale) = -1, quand elles passent toutes deux par le même point du graphique.[4] En d'autres termes: - Trouvez f '(x), la pente de la ligne tangente.
- Si le point est à x = une, trouvez f '(a) pour trouver la pente de la tangente à ce point.
- Calculer pour trouver la pente de la normale.
- Écrivez l'équation normale sous forme de pente.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Esquissez la fonction et la ligne tangente (recommandé). Un graphique facilite le suivi du problème et vérifie la pertinence de la réponse. Dessinez la fonction sur un morceau de papier millimétré, en utilisant une calculatrice graphique comme référence si nécessaire. Esquissez la ligne tangente passant par le point donné. (Rappelez-vous que la ligne tangente traverse ce point et a la même pente que le graphique à cet endroit.)
1 Esquissez la fonction et la ligne tangente (recommandé). Un graphique facilite le suivi du problème et vérifie la pertinence de la réponse. Dessinez la fonction sur un morceau de papier millimétré, en utilisant une calculatrice graphique comme référence si nécessaire. Esquissez la ligne tangente passant par le point donné. (Rappelez-vous que la ligne tangente traverse ce point et a la même pente que le graphique à cet endroit.) 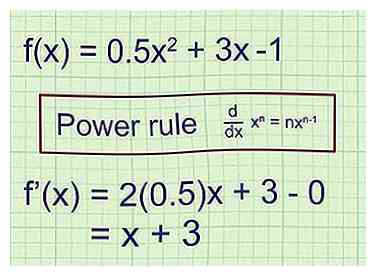 2 Prenez le premier dérivé pour trouver l'équation du pente de la ligne tangente. Pour la fonction f (x), la première dérivée f '(x) représente l’équation de la pente de la tangente en tout point de f (x). Il y a plusieurs façons de prendre des dérivés. Voici un exemple simple utilisant la règle de puissance:[1]
2 Prenez le premier dérivé pour trouver l'équation du pente de la ligne tangente. Pour la fonction f (x), la première dérivée f '(x) représente l’équation de la pente de la tangente en tout point de f (x). Il y a plusieurs façons de prendre des dérivés. Voici un exemple simple utilisant la règle de puissance:[1] 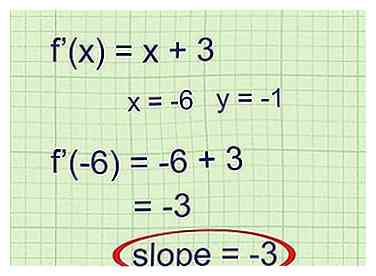 3 Entrez la valeur x du point que vous étudiez. Lisez le problème pour découvrir les coordonnées du point pour lequel vous trouvez la ligne tangente. Entrez la coordonnée x de ce point dans f '(x). La sortie est la pente de la ligne tangente à ce point.
3 Entrez la valeur x du point que vous étudiez. Lisez le problème pour découvrir les coordonnées du point pour lequel vous trouvez la ligne tangente. Entrez la coordonnée x de ce point dans f '(x). La sortie est la pente de la ligne tangente à ce point. 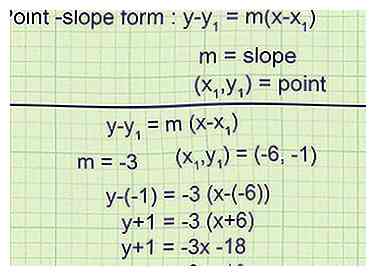 4 Écrivez l'équation de la ligne tangente en forme de pente ponctuelle. La forme point-pente d'une équation linéaire est
4 Écrivez l'équation de la ligne tangente en forme de pente ponctuelle. La forme point-pente d'une équation linéaire est  5 Confirmez l'équation sur votre graphique. Si vous avez une calculatrice graphique, tracez la fonction d'origine et la ligne tangente pour vérifier que vous avez la bonne réponse. Si vous travaillez sur papier, reportez-vous à votre graphique précédent pour vous assurer qu’il n’ya pas d’erreurs flagrantes dans votre réponse.
5 Confirmez l'équation sur votre graphique. Si vous avez une calculatrice graphique, tracez la fonction d'origine et la ligne tangente pour vérifier que vous avez la bonne réponse. Si vous travaillez sur papier, reportez-vous à votre graphique précédent pour vous assurer qu’il n’ya pas d’erreurs flagrantes dans votre réponse.  6 Essayez un problème plus difficile. Voici un aperçu de tout le processus à nouveau. Cette fois, le but est de trouver la ligne tangente à
6 Essayez un problème plus difficile. Voici un aperçu de tout le processus à nouveau. Cette fois, le but est de trouver la ligne tangente à  1 Trouvez les points extrêmes sur un graphique. Ce sont des points où le graphique atteint un maximum local (un point supérieur aux points de chaque côté) ou un minimum local (inférieur aux points de chaque côté). La ligne tangente a toujours une pente de 0 à ces points (une ligne horizontale), mais une pente nulle seule ne garantit pas un point extrême. Voici comment les trouver:[3]
1 Trouvez les points extrêmes sur un graphique. Ce sont des points où le graphique atteint un maximum local (un point supérieur aux points de chaque côté) ou un minimum local (inférieur aux points de chaque côté). La ligne tangente a toujours une pente de 0 à ces points (une ligne horizontale), mais une pente nulle seule ne garantit pas un point extrême. Voici comment les trouver:[3]  2 Trouvez l'équation de la normale. La "normale" à une courbe à un point particulier passe par ce point, mais a une pente perpendiculaire à une tangente. Pour trouver l'équation de la normale, profitez du fait que (pente de la tangente) (pente de la normale) = -1, quand elles passent toutes deux par le même point du graphique.[4] En d'autres termes:
2 Trouvez l'équation de la normale. La "normale" à une courbe à un point particulier passe par ce point, mais a une pente perpendiculaire à une tangente. Pour trouver l'équation de la normale, profitez du fait que (pente de la tangente) (pente de la normale) = -1, quand elles passent toutes deux par le même point du graphique.[4] En d'autres termes: