Le périmètre est une mesure de la surface ou de la distance autour d'une forme bidimensionnelle. Par exemple, sur un rectangle, le périmètre est la longueur totale du contour du rectangle, y compris les deux bordures en largeur et les deux bordures longitudinales. Pour déterminer le périmètre d'une forme, vous ajoutez donc toutes les dimensions qui composent le bord extérieur de la forme. Pouvoir trouver le périmètre d'une forme a de nombreuses applications dans le monde réel. Disons, par exemple, que vous vouliez construire une clôture autour de votre cour. Pour acheter du matériel, vous devez connaître le nombre de clôtures dont vous avez besoin et déterminer le périmètre de la zone dans laquelle vous souhaitez clôturer.
Première partie de deux:
Trouver le périmètre de la plupart des formes
-
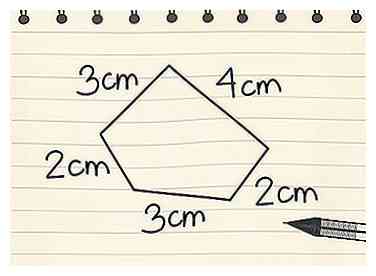 1 Détermine la longueur de chaque côté. Étant donné que le périmètre n'est qu'une mesure du contour d'une figure à deux dimensions, vous n'avez généralement pas besoin d'une formule spécifique pour trouver un périmètre (bien qu'il existe des équations pour des formes spécifiques afin de le rendre plus facile). Cependant, vous devez connaître la longueur de tous les côtés de la forme.[1]
1 Détermine la longueur de chaque côté. Étant donné que le périmètre n'est qu'une mesure du contour d'une figure à deux dimensions, vous n'avez généralement pas besoin d'une formule spécifique pour trouver un périmètre (bien qu'il existe des équations pour des formes spécifiques afin de le rendre plus facile). Cependant, vous devez connaître la longueur de tous les côtés de la forme.[1] - Par exemple, un pentagone a cinq côtés et vous devez connaître la longueur de chacun pour déterminer le périmètre.
- Même avec un polygone irrégulier qui a 20 côtés, vous pouvez toujours trouver le périmètre tant que vous connaissez la longueur de chaque côté.
-
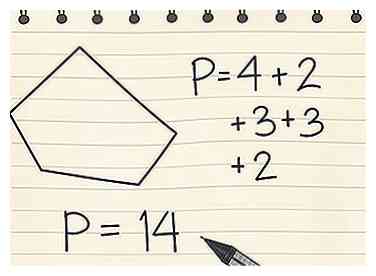 2 Ajouter la longueur de tous les côtés ensemble. Pour trouver le périmètre des objets non circulaires, recherchez la somme de toutes les longueurs latérales pour déterminer la distance autour de la forme.[2]
2 Ajouter la longueur de tous les côtés ensemble. Pour trouver le périmètre des objets non circulaires, recherchez la somme de toutes les longueurs latérales pour déterminer la distance autour de la forme.[2] - Disons que le pentagone irrégulier a les longueurs suivantes: A = 4, B = 2, C = 3, D = 3 et E = 2
- Ajouter 4 + 2 + 3 + 3 + 2 = 14, où P (périmètre) = 14
-
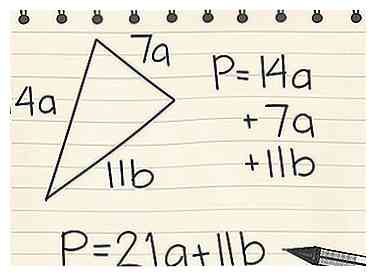 3 Traiter les variables. Vous pouvez toujours trouver un périmètre lorsque vous travaillez avec des variables. Par exemple, supposons que vous avez un triangle avec les longueurs latérales 14a, 11b et 7a:[3]
3 Traiter les variables. Vous pouvez toujours trouver un périmètre lorsque vous travaillez avec des variables. Par exemple, supposons que vous avez un triangle avec les longueurs latérales 14a, 11b et 7a:[3] - Trouvez la somme de tous les côtés: P = 14a + 11b + 7a
- Combinez les termes similaires: P = (14a + 7a) + 11b
- P = 21a + 11b
-
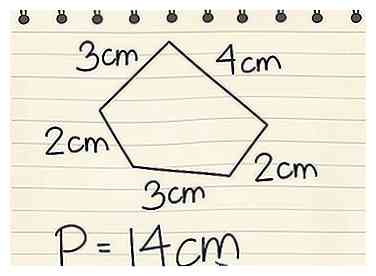 4 Faites attention aux unités de mesure. Dans une application du monde réel, trouver le périmètre d'un objet ne vous sera pas d'une grande utilité si vous ne savez pas avec quelle unité de mesure vous travaillez (pieds, miles ou mètres, par exemple). Avec le pentagone, si chaque côté était mesuré en centimètres, alors vous savez que P = 14 cm.
4 Faites attention aux unités de mesure. Dans une application du monde réel, trouver le périmètre d'un objet ne vous sera pas d'une grande utilité si vous ne savez pas avec quelle unité de mesure vous travaillez (pieds, miles ou mètres, par exemple). Avec le pentagone, si chaque côté était mesuré en centimètres, alors vous savez que P = 14 cm.
Deuxième partie de deux:
Apprentissage des formules de périmètre
-
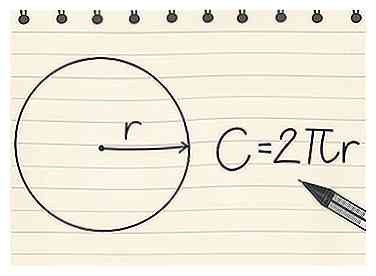 1 Trouvez le périmètre d'un cercle. Certaines formes régulières ont des formules qui vous permettent de trouver plus rapidement le périmètre de la figure. Mais il existe d'autres formes, comme des cercles, qui nécessitent une formule pour trouver un périmètre. Le périmètre d'un cercle s'appelle la circonférence. Pour trouver la circonférence d'un cercle, utilisez l'équation C (circonférence) = 2πr.[4]
1 Trouvez le périmètre d'un cercle. Certaines formes régulières ont des formules qui vous permettent de trouver plus rapidement le périmètre de la figure. Mais il existe d'autres formes, comme des cercles, qui nécessitent une formule pour trouver un périmètre. Le périmètre d'un cercle s'appelle la circonférence. Pour trouver la circonférence d'un cercle, utilisez l'équation C (circonférence) = 2πr.[4] - Pour commencer, recherchez le rayon du cercle, qui est la longueur d'un segment de ligne allant du centre du cercle jusqu'au périmètre.
- Pour des équations plus simples, utilisez la version tronquée π = 3.14
- Pour un cercle de rayon de 4cm: C = 2 x 3.14 x 4 = 25.12cm
-
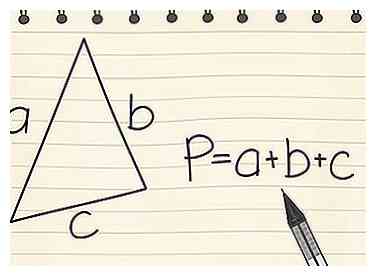 2 Trouvez le périmètre d'un triangle. Utilisez l'équation P = a + b + c pour un triangle. Par exemple, si un triangle a les dimensions a = 20cm, b = 11cm et c = 9cm, alors P = 20 + 11 + 9 = 40cm.
2 Trouvez le périmètre d'un triangle. Utilisez l'équation P = a + b + c pour un triangle. Par exemple, si un triangle a les dimensions a = 20cm, b = 11cm et c = 9cm, alors P = 20 + 11 + 9 = 40cm. -
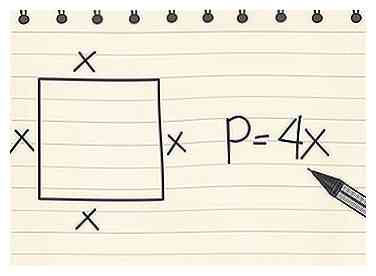 3 Trouve le périmètre d'un carré. Comme un carré a quatre côtés de même longueur, vous pouvez utiliser l'équation simple P = 4x, où x est égal à la longueur d'un côté.
3 Trouve le périmètre d'un carré. Comme un carré a quatre côtés de même longueur, vous pouvez utiliser l'équation simple P = 4x, où x est égal à la longueur d'un côté. - Sur un carré où x = 3cm, alors P = 4 x 3 = 12cm
-
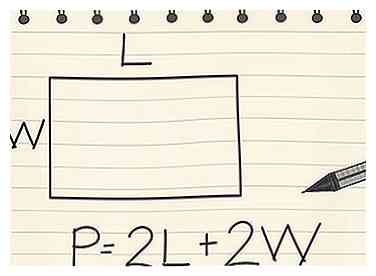 4 Trouvez le périmètre d'un rectangle. Comme les côtés longitudinaux sont identiques et que les côtés largeur sont identiques sur un rectangle, vous pouvez utiliser l'équation P = 2l + 2w, où l est la longueur d'un côté et w la largeur d'un côté. Pour un rectangle où l = 8cm et w = 5cm:
4 Trouvez le périmètre d'un rectangle. Comme les côtés longitudinaux sont identiques et que les côtés largeur sont identiques sur un rectangle, vous pouvez utiliser l'équation P = 2l + 2w, où l est la longueur d'un côté et w la largeur d'un côté. Pour un rectangle où l = 8cm et w = 5cm: - P = (2 x 8) + (2 x 5)
- P = 16 + 10
- P = 26cm
- L'équation P = 2 (l + h) vous donnera également le même résultat: 2 (8 + 5) = 2 (13) = 26cm[5]
-
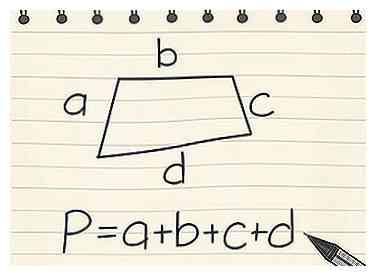 5 Trouvez le périmètre des autres quadrilatères. Un quadrilatère fait référence à toute forme bidimensionnelle avec quatre côtés droits et fermés. Cela comprend des rectangles, des carrés, des trapèzes, des parallélogrammes, des cerfs-volants et des losanges.[6] Vous pouvez utiliser trois équations pour un quadrilatère, selon les côtés:
5 Trouvez le périmètre des autres quadrilatères. Un quadrilatère fait référence à toute forme bidimensionnelle avec quatre côtés droits et fermés. Cela comprend des rectangles, des carrés, des trapèzes, des parallélogrammes, des cerfs-volants et des losanges.[6] Vous pouvez utiliser trois équations pour un quadrilatère, selon les côtés: - Pour un quadrilatère sans côtés égaux, comme un trapèze irrégulier, utilisez l'équation P = a + b + c + d
- Pour un quadrilatère à quatre côtés égaux, utilisez la même équation qu'un carré: P = 4x.
- Pour les quadrilatères où les côtés longitudinaux sont identiques et les côtés en largeur identiques (comme un rectangle), utilisez les équations P = 2a + 2b ou P = 2 (a + b)
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Détermine la longueur de chaque côté. Étant donné que le périmètre n'est qu'une mesure du contour d'une figure à deux dimensions, vous n'avez généralement pas besoin d'une formule spécifique pour trouver un périmètre (bien qu'il existe des équations pour des formes spécifiques afin de le rendre plus facile). Cependant, vous devez connaître la longueur de tous les côtés de la forme.[1]
1 Détermine la longueur de chaque côté. Étant donné que le périmètre n'est qu'une mesure du contour d'une figure à deux dimensions, vous n'avez généralement pas besoin d'une formule spécifique pour trouver un périmètre (bien qu'il existe des équations pour des formes spécifiques afin de le rendre plus facile). Cependant, vous devez connaître la longueur de tous les côtés de la forme.[1]  2 Ajouter la longueur de tous les côtés ensemble. Pour trouver le périmètre des objets non circulaires, recherchez la somme de toutes les longueurs latérales pour déterminer la distance autour de la forme.[2]
2 Ajouter la longueur de tous les côtés ensemble. Pour trouver le périmètre des objets non circulaires, recherchez la somme de toutes les longueurs latérales pour déterminer la distance autour de la forme.[2]  3 Traiter les variables. Vous pouvez toujours trouver un périmètre lorsque vous travaillez avec des variables. Par exemple, supposons que vous avez un triangle avec les longueurs latérales 14a, 11b et 7a:[3]
3 Traiter les variables. Vous pouvez toujours trouver un périmètre lorsque vous travaillez avec des variables. Par exemple, supposons que vous avez un triangle avec les longueurs latérales 14a, 11b et 7a:[3]  4 Faites attention aux unités de mesure. Dans une application du monde réel, trouver le périmètre d'un objet ne vous sera pas d'une grande utilité si vous ne savez pas avec quelle unité de mesure vous travaillez (pieds, miles ou mètres, par exemple). Avec le pentagone, si chaque côté était mesuré en centimètres, alors vous savez que P = 14 cm.
4 Faites attention aux unités de mesure. Dans une application du monde réel, trouver le périmètre d'un objet ne vous sera pas d'une grande utilité si vous ne savez pas avec quelle unité de mesure vous travaillez (pieds, miles ou mètres, par exemple). Avec le pentagone, si chaque côté était mesuré en centimètres, alors vous savez que P = 14 cm. 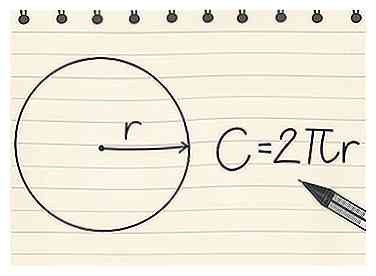 1 Trouvez le périmètre d'un cercle. Certaines formes régulières ont des formules qui vous permettent de trouver plus rapidement le périmètre de la figure. Mais il existe d'autres formes, comme des cercles, qui nécessitent une formule pour trouver un périmètre. Le périmètre d'un cercle s'appelle la circonférence. Pour trouver la circonférence d'un cercle, utilisez l'équation C (circonférence) = 2πr.[4]
1 Trouvez le périmètre d'un cercle. Certaines formes régulières ont des formules qui vous permettent de trouver plus rapidement le périmètre de la figure. Mais il existe d'autres formes, comme des cercles, qui nécessitent une formule pour trouver un périmètre. Le périmètre d'un cercle s'appelle la circonférence. Pour trouver la circonférence d'un cercle, utilisez l'équation C (circonférence) = 2πr.[4]  2 Trouvez le périmètre d'un triangle. Utilisez l'équation P = a + b + c pour un triangle. Par exemple, si un triangle a les dimensions a = 20cm, b = 11cm et c = 9cm, alors P = 20 + 11 + 9 = 40cm.
2 Trouvez le périmètre d'un triangle. Utilisez l'équation P = a + b + c pour un triangle. Par exemple, si un triangle a les dimensions a = 20cm, b = 11cm et c = 9cm, alors P = 20 + 11 + 9 = 40cm. 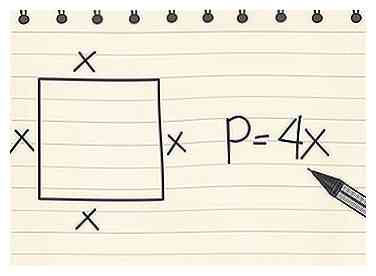 3 Trouve le périmètre d'un carré. Comme un carré a quatre côtés de même longueur, vous pouvez utiliser l'équation simple P = 4x, où x est égal à la longueur d'un côté.
3 Trouve le périmètre d'un carré. Comme un carré a quatre côtés de même longueur, vous pouvez utiliser l'équation simple P = 4x, où x est égal à la longueur d'un côté.  4 Trouvez le périmètre d'un rectangle. Comme les côtés longitudinaux sont identiques et que les côtés largeur sont identiques sur un rectangle, vous pouvez utiliser l'équation P = 2l + 2w, où l est la longueur d'un côté et w la largeur d'un côté. Pour un rectangle où l = 8cm et w = 5cm:
4 Trouvez le périmètre d'un rectangle. Comme les côtés longitudinaux sont identiques et que les côtés largeur sont identiques sur un rectangle, vous pouvez utiliser l'équation P = 2l + 2w, où l est la longueur d'un côté et w la largeur d'un côté. Pour un rectangle où l = 8cm et w = 5cm:  5 Trouvez le périmètre des autres quadrilatères. Un quadrilatère fait référence à toute forme bidimensionnelle avec quatre côtés droits et fermés. Cela comprend des rectangles, des carrés, des trapèzes, des parallélogrammes, des cerfs-volants et des losanges.[6] Vous pouvez utiliser trois équations pour un quadrilatère, selon les côtés:
5 Trouvez le périmètre des autres quadrilatères. Un quadrilatère fait référence à toute forme bidimensionnelle avec quatre côtés droits et fermés. Cela comprend des rectangles, des carrés, des trapèzes, des parallélogrammes, des cerfs-volants et des losanges.[6] Vous pouvez utiliser trois équations pour un quadrilatère, selon les côtés: