Ce tutoriel contient des instructions étape par étape sur la façon d'écrire un script qui représente graphiquement une fonction par morceaux. Bien que la programmation puisse sembler une tâche décourageante pour ceux qui sont novices, ces instructions vous assureront que vous n'aurez aucun problème à programmer un code qui représente graphiquement une fonction par morceaux dans MATLAB. Pour ce tutoriel, nous allons prendre les équations x ^ 2 - 3x + 12 (0 <= x <= 2), x ^ 3 + 5 (3 <= x <5), x ^ 2 - 22 (6 <= x <8), x ^ 2 + 12 (8
Pas
- 1 Ouvrez MATLAB.
- 2
 Déplacez votre souris à l'extrême gauche de la barre de l'éditeur et cliquez sur l'icône indiquant le nouveau script.
Déplacez votre souris à l'extrême gauche de la barre de l'éditeur et cliquez sur l'icône indiquant le nouveau script. - Cela ouvrira une fenêtre appelée un script juste au-dessus de votre menu de commandes, qui se trouve au milieu de votre écran.
- 3 Commencez votre script en invitant l'utilisateur à saisir une valeur numérique pour le caractère x (nous pouvons affecter n'importe quel caractère à cette valeur, mais nous allons utiliser x). Cette valeur sera ce qui entre dans les fonctions qui vont être représentées graphiquement.
- 4 Tapez x = input () dans votre script en tant que votre première ligne. Cela utilise la commande d'entrée de MATLAB qui permet à l'utilisateur de taper n'importe quel nombre dans le menu de commande après l'appel du script (cela sera montré plus loin dans ces instructions).
- 5 Écrivez le type valeur numérique pour x dans les parenthèses de votre commande d'entrée. Il devrait ressembler à x = input ('tapez la valeur numérique pour x:'). Lorsque l'utilisateur appelle le script, celui-ci apparaîtra dans le menu de commande, invitant l'utilisateur à attribuer une valeur numérique au caractère x. Votre première ligne est maintenant terminée.
- 6 Définissez les quatre équations comme une fonction anonyme pour les caractères f1, f2, f3 et f4 sur des lignes séparées en commençant par «f1» comme ligne deux et en terminant par «f4» en tant que ligne cinq. C'est la seule façon dont les équations peuvent être à l'intérieur du script et s'exécuter correctement.
- Lorsque vous écrivez votre fonction ou votre équation, il est important que vous connaissiez les équivalents arithmétiques dans MATLAB, afin que MATLAB puisse lire votre code. L'addition est +, la soustraction est -, la multiplication est *, la division est / et l'exponentiation est ^.
- Il est non seulement important que vous ayez les bons symboles que vous devez utiliser un opérateur de point chaque fois que vous multipliez, divisez ou pour exprimer un vecteur de valeurs dans votre équation. L'opérateur de points est une période. Pour que vous puissiez l'utiliser, vous devez la placer devant votre multiplication, division et exponentiation. Il devrait ressembler à 2. * 2 + 5-2. ^ 2
- 7 Choisissez le caractère que vous souhaitez attribuer à votre fonction ou à votre équation. Il devrait suivre l'ordre des caractères = function. En utilisant la première fonction comme exemple, il devrait ressembler à «f1 = x. ^ 2 - 3. * x + 12»
-
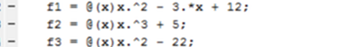 8 Ajoutez un "@ (caractère de saisie)" devant votre fonction. Il devrait ressembler à la fonction «caractère = @ (caractère de saisie)». Terminer votre première fonction devrait ressembler à «f1 = @ (x) x. ^ 2 - 3. * x + 12».
8 Ajoutez un "@ (caractère de saisie)" devant votre fonction. Il devrait ressembler à la fonction «caractère = @ (caractère de saisie)». Terminer votre première fonction devrait ressembler à «f1 = @ (x) x. ^ 2 - 3. * x + 12». - 9 Créez une instruction conditionnelle «if» sur la ligne six de votre script. Cela vous permet de créer des conditions correspondant au domaine de chacune de vos fonctions par morceaux. Si les conditions sont remplies, le programme exécutera le code des lignes immédiatement après votre condition. Si les conditions ne sont pas vraies, MATLAB ira vérifier les conditions dans la ligne la plus proche avec des instructions conditionnelles, en continuant jusqu'à ce que toutes les conditions soient remplies ou qu'aucune condition ne soit laissée.
- 10 Suivez votre instruction conditionnelle sur la ligne six, vous devez écrire les conditions à l'aide des opérateurs logiques de MATLAB. Les opérateurs logiques nécessaires pour cela sont &,>, <,> =, <=. Pour ignorer l'opérateur &, vous avez un nombre supérieur, inférieur, supérieur ou égal à, et inférieur ou égal à. L'opérateur & est un cas particulier en ce qu'il indique à MATLAB que toutes les instructions conditionnelles sur la ligne doivent être vraies pour la valeur x entrée manuellement afin d'exécuter le code, sinon MATLAB passera à tester la valeur dans la ligne suivante avec conditionnelle déclarations.
- 11 Écrivez x> = 0 & x <2 après l'instruction if pour terminer la ligne six. Ceci est fait parce que la fonction f1 = @ (x) x. ^ 2 - 3. * x + 12 est comprise entre zéro et deux, sauf deux, et l'état conditionnel satisfait le domaine.
- 12Sur les lignes sept et huit, vous devez écrire le code à exécuter si les conditions de la ligne six sont remplies.
- 13 Écrivez y = f1 (x) sur la ligne sept. Cela indique au script l'équation à représenter graphiquement en fonction de la valeur x saisie manuellement par l'utilisateur.
- 14
 Écrivez fplot (f1, [0,2]) sur la ligne huit. Cela utilise la commande fplot dans MATLAB qui permet à l'utilisateur de tracer des fonctions anonymes. f1 est la fonction représentée graphiquement, tandis que [0,2] est le domaine du graphique.
Écrivez fplot (f1, [0,2]) sur la ligne huit. Cela utilise la commande fplot dans MATLAB qui permet à l'utilisateur de tracer des fonctions anonymes. f1 est la fonction représentée graphiquement, tandis que [0,2] est le domaine du graphique. - 15 Utilisez l'instruction conditionnelle elseif sur la ligne neuf. Ceci est essentiellement le même que l'instruction if, mais vous utilisez elseif afin que MATLAB suive complètement votre code. Si vous utilisez if au lieu de elseif, alors MATLAB verra deux branches de codes distinctes dans un script, ce qui est préjudiciable car nous en avons besoin pour fonctionner comme un seul.
- 16 Suivez votre énoncé conditionnel elseif sur la ligne neuf. Écrivez les conditions similaires à la façon dont cela a été fait après l'instruction if.
- 17 Écrivez x> = 3 & x <5 après l'instruction elseif pour compléter la ligne neuf. Ceci est fait parce que la fonction f2 = @ (x) x. ^ 3 + 5; domain est compris entre trois et cinq, sauf cinq, et l'instruction conditionnelle satisfait le domaine.
- 18Écrivez le code à exécuter si les conditions de la ligne neuf sont remplies aux lignes 10 et 11.
- 19 Écrivez y = f2 (x) sur la ligne dix. Cela indique au script l'équation à représenter graphiquement en fonction de la valeur x saisie manuellement par l'utilisateur.
- 20
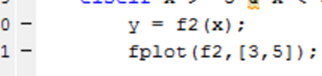 Écrivez fplot (f2, [3,5]) sur la ligne onze. Cela utilise la commande fplot dans MATLAB.f2 est la fonction représentée graphiquement, tandis que [3,5] est le domaine du graphique.
Écrivez fplot (f2, [3,5]) sur la ligne onze. Cela utilise la commande fplot dans MATLAB.f2 est la fonction représentée graphiquement, tandis que [3,5] est le domaine du graphique. - 21Utilisez l'instruction conditionnelle elseif sur la ligne 12.
- 22Suivez votre énoncé conditionnel sur la ligne douze, vous devez écrire les conditions.
- 23 Écrivez x> = 6 & x <8 après la déclaration elseif pour compléter la ligne douze. Ceci est fait parce que la fonction “f3 = @ (x) x. ^ 2 - 22” est comprise entre six et huit, à l’exception de huit, et que l’instruction conditionnelle satisfait le domaine.
- 24 Écrivez le code à exécuter si les conditions de la ligne douze sont remplies. Le 12 et le 13
- 25 Écrivez y = f3 (x) sur la ligne treize. Cela indique au script l'équation à représenter graphiquement en fonction de la valeur x saisie manuellement par l'utilisateur.
- 26
 Ecrivez fplot (f3, [6,8]) sur la ligne quatorze. Cela utilise la commande fplot dans MATLAB. f3 est la fonction représentée graphiquement, alors que [6,8] est le domaine du graphique.
Ecrivez fplot (f3, [6,8]) sur la ligne quatorze. Cela utilise la commande fplot dans MATLAB. f3 est la fonction représentée graphiquement, alors que [6,8] est le domaine du graphique. - 27Utilisez la déclaration conditionnelle elseif sur la ligne 15.
- 28Suivez votre énoncé conditionnel sur la ligne quinze, vous devez écrire les conditions.
- 29 Écrivez x> 8 & x <= 10 après la déclaration elseif pour compléter la ligne quinze. Ceci est fait parce que la fonction f4 = @ (x) x. ^ 2 + 12 est comprise entre huit et dix, à l’exception de huit, et que l’instruction conditionnelle satisfait le domaine.
- 30 Écrivez le code à exécuter si les conditions de la ligne quinze sont remplies. Aux lignes 16 et 17.
- 31 Écrivez y = f4 (x) à la ligne seize. Cela indique au script l'équation à représenter graphiquement en fonction de la valeur x saisie manuellement par l'utilisateur.
- 32
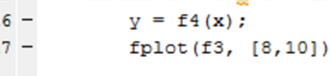 Ecrivez fplot (f3, [8,10]) sur la ligne dix-sept. Cela utilise la commande fplot dans MATLAB. f4 est la fonction représentée graphiquement, tandis que [8,10] est le domaine du graphique.
Ecrivez fplot (f3, [8,10]) sur la ligne dix-sept. Cela utilise la commande fplot dans MATLAB. f4 est la fonction représentée graphiquement, tandis que [8,10] est le domaine du graphique. - 33 Utilisez la déclaration conditionnelle else. Ce qui est essentiellement le même que les instructions conditionnelles if et elseif, mais c'est la dernière instruction conditionnelle que MATLAB lit après avoir testé tous les autres. Essentiellement, les codes qui suivent cette instruction sont les derniers à être exécutés.
- 34Dites au script d'afficher hors de portée en utilisant la commande d'affichage dans MATLAB sur la ligne 19.
- 35Ecrire disp (hors de portée).
- 36
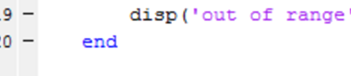 À la vingtième ligne, terminez le script en écrivant à la fin.
À la vingtième ligne, terminez le script en écrivant à la fin. - 37 Cliquez avec le bouton droit sur l'emplacement de sauvegarde avec une disquette en guise d'icône. Il se trouve dans l'onglet Editeurs, et se trouve à un emplacement de l'icône de gauche la plus éloignée appelée nouvelle et comportant une croix pour une icône.
- Une liste déroulante devrait apparaître, si ce n'est pas le cas, vous pouvez utiliser le raccourci «ctrl + s». Cliquez sur enregistrer sous.
- 38 Tapez le nom dans lequel vous avez enregistré votre fichier de script dans la fenêtre de commande pour appeler votre script (appeler un script signifie utiliser ou initialiser votre code de scripts).). Après avoir appelé votre script, il doit vous demander de saisir une valeur x dans la fenêtre de commande en indiquant la valeur numérique de type pour x.
-
 39 Tapez toute valeur que vous voulez que x soit. Tout nombre compris entre zéro et dix vous donnera un graphique avec l'une des fonctions, sauf pour deux, cinq et huit. Deux, cinq, huit et n'importe quel nombre en dehors de zéro à dix vous indiqueront que vous êtes hors de portée dans la fenêtre de commande. Vous avez maintenant un code de travail pour un graphique par morceaux. Ci-dessus est un exemple de comment appeler votre script. Le nom utilisé est callcript, et la valeur numérique de x est trois.
39 Tapez toute valeur que vous voulez que x soit. Tout nombre compris entre zéro et dix vous donnera un graphique avec l'une des fonctions, sauf pour deux, cinq et huit. Deux, cinq, huit et n'importe quel nombre en dehors de zéro à dix vous indiqueront que vous êtes hors de portée dans la fenêtre de commande. Vous avez maintenant un code de travail pour un graphique par morceaux. Ci-dessus est un exemple de comment appeler votre script. Le nom utilisé est callcript, et la valeur numérique de x est trois.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 Déplacez votre souris à l'extrême gauche de la barre de l'éditeur et cliquez sur l'icône indiquant le nouveau script.
Déplacez votre souris à l'extrême gauche de la barre de l'éditeur et cliquez sur l'icône indiquant le nouveau script. 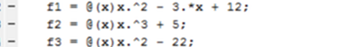 8 Ajoutez un "@ (caractère de saisie)" devant votre fonction. Il devrait ressembler à la fonction «caractère = @ (caractère de saisie)». Terminer votre première fonction devrait ressembler à «f1 = @ (x) x. ^ 2 - 3. * x + 12».
8 Ajoutez un "@ (caractère de saisie)" devant votre fonction. Il devrait ressembler à la fonction «caractère = @ (caractère de saisie)». Terminer votre première fonction devrait ressembler à «f1 = @ (x) x. ^ 2 - 3. * x + 12».  Écrivez fplot (f1, [0,2]) sur la ligne huit. Cela utilise la commande fplot dans MATLAB qui permet à l'utilisateur de tracer des fonctions anonymes. f1 est la fonction représentée graphiquement, tandis que [0,2] est le domaine du graphique.
Écrivez fplot (f1, [0,2]) sur la ligne huit. Cela utilise la commande fplot dans MATLAB qui permet à l'utilisateur de tracer des fonctions anonymes. f1 est la fonction représentée graphiquement, tandis que [0,2] est le domaine du graphique. 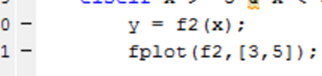 Écrivez fplot (f2, [3,5]) sur la ligne onze. Cela utilise la commande fplot dans MATLAB.f2 est la fonction représentée graphiquement, tandis que [3,5] est le domaine du graphique.
Écrivez fplot (f2, [3,5]) sur la ligne onze. Cela utilise la commande fplot dans MATLAB.f2 est la fonction représentée graphiquement, tandis que [3,5] est le domaine du graphique.  Ecrivez fplot (f3, [6,8]) sur la ligne quatorze. Cela utilise la commande fplot dans MATLAB. f3 est la fonction représentée graphiquement, alors que [6,8] est le domaine du graphique.
Ecrivez fplot (f3, [6,8]) sur la ligne quatorze. Cela utilise la commande fplot dans MATLAB. f3 est la fonction représentée graphiquement, alors que [6,8] est le domaine du graphique. 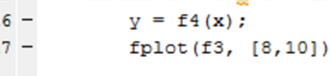 Ecrivez fplot (f3, [8,10]) sur la ligne dix-sept. Cela utilise la commande fplot dans MATLAB. f4 est la fonction représentée graphiquement, tandis que [8,10] est le domaine du graphique.
Ecrivez fplot (f3, [8,10]) sur la ligne dix-sept. Cela utilise la commande fplot dans MATLAB. f4 est la fonction représentée graphiquement, tandis que [8,10] est le domaine du graphique.  À la vingtième ligne, terminez le script en écrivant à la fin.
À la vingtième ligne, terminez le script en écrivant à la fin.  39 Tapez toute valeur que vous voulez que x soit. Tout nombre compris entre zéro et dix vous donnera un graphique avec l'une des fonctions, sauf pour deux, cinq et huit. Deux, cinq, huit et n'importe quel nombre en dehors de zéro à dix vous indiqueront que vous êtes hors de portée dans la fenêtre de commande. Vous avez maintenant un code de travail pour un graphique par morceaux. Ci-dessus est un exemple de comment appeler votre script. Le nom utilisé est callcript, et la valeur numérique de x est trois.
39 Tapez toute valeur que vous voulez que x soit. Tout nombre compris entre zéro et dix vous donnera un graphique avec l'une des fonctions, sauf pour deux, cinq et huit. Deux, cinq, huit et n'importe quel nombre en dehors de zéro à dix vous indiqueront que vous êtes hors de portée dans la fenêtre de commande. Vous avez maintenant un code de travail pour un graphique par morceaux. Ci-dessus est un exemple de comment appeler votre script. Le nom utilisé est callcript, et la valeur numérique de x est trois.